Symbolic Discovery of Optimization Algorithms

https://arxiv.org/abs/2302.06675

Symbolic Discovery of Optimization Algorithms

 

초록
우리는 알고리즘 발견을 프로그램 탐색(program search) 문제로 공식화하는 방법을 제안하고, 이를 딥 뉴럴 네트워크 학습을 위한 최적화 알고리즘 발견에 적용한다. 본 연구는 무한하고 희소한 프로그램 공간을 효율적으로 탐색하기 위해 고속 탐색 기법을 활용하며, 프록시(proxy) 태스크와 실제(target) 태스크 간의 큰 일반화 차이를 줄이기 위해 프로그램 선택 및 단순화 전략도 도입한다. 이러한 접근을 통해 간단하면서도 효과적인 최적화 알고리즘인 Lion (EvoLved Sign Momentum) 을 발견하였다. Lion은 모멘텀만을 유지하므로 Adam보다 더 메모리 효율적이다. 또한 적응형(adaptive) 옵티마이저들과 달리, 각 파라미터의 업데이트는 부호(sign) 연산을 통해 동일한 크기를 가지게 된다.

 

우리는 Lion을 Adam, Adafactor와 같은 널리 사용되는 옵티마이저들과 비교하여, 다양한 태스크에서 여러 모델을 학습시켜 성능을 평가하였다. 이미지 분류에서는, Lion이 ViT의 ImageNet 정확도를 최대 2% 향상시키고, JFT에서 사전학습(pre-training) 연산량을 최대 5배까지 절감한다. 비전-언어(vision-language) 대조 학습(contrastive learning)에서는 ImageNet에서 제로샷(Zero-shot) 88.3%, 파인튜닝(fine-tuning) 91.1%의 정확도를 달성하며, 각각 기존 최고 성능을 2%, 0.1% 상회하였다. 디퓨전 모델에서는 Lion이 Adam보다 더 나은 FID 점수를 기록하고 학습 연산량을 최대 2.3배까지 줄였다. 오토리그레시브(autoregressive), 마스킹 언어 모델링(masked language modeling), 파인튜닝에서도 Lion은 Adam과 유사하거나 더 나은 성능을 보였다.

 

Lion에 대한 분석 결과, 학습 배치 크기가 클수록 성능 향상이 더 크며, 부호 연산으로 인해 업데이트의 노름(norm)이 커지기 때문에 Adam보다 작은 학습률이 필요함을 확인하였다. 또한, Lion의 한계를 검토하여 일부 상황에서는 개선 효과가 작거나 통계적으로 유의하지 않음을 밝혔다.

 

Lion의 구현체는 공개되어 있으며[링크](https://github.com/google/automl/tree/master/lion), Google 검색 광고의 CTR 예측 모델 등 실제 프로덕션 시스템에도 성공적으로 적용되고 있다.

문의: xiangning@cs.ucla.edu, crazydonkey@google.com

 

1. 서론 (Introduction)

최적화 알고리즘(optimizer)은 신경망 학습에서 핵심적인 역할을 한다. 최근 몇 년간 많은 수작업으로 설계된, 대부분은 적응형(adaptive) 최적화 기법들이 제안되어 왔다(Zhuang et al., 2020; Balles and Hennig, 2018; Liu et al., 2020; Bernstein et al., 2018; Dozat, 2016; Anil et al., 2020). 그러나 실제로는 Adam(Kingma and Ba, 2014)과 그 변형인 AdamW(Loshchilov and Hutter, 2019), 그리고 Adafactor(Shazeer and Stern, 2018)가 여전히 대부분의 딥 뉴럴 네트워크 학습에 있어 사실상의 표준 최적화기로 사용되고 있다. 특히 최신 언어 모델(Brown et al., 2020; Vaswani et al., 2017; Devlin et al., 2019), 비전 모델(Dosovitskiy et al., 2021; Dai et al., 2021; Zhai et al., 2021), 멀티모달 모델(Radford et al., 2021; Saharia et al., 2022; Yu et al., 2022)에서 두드러진다.

 

표 1: BASIC-L (Pham et al., 2021)의 ImageNet 및 강인성 벤치마크 정확도

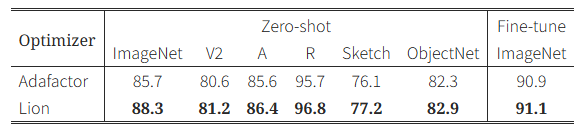
우리는 Lion을 비전 타워 사전학습과 비전-언어 대조 학습 두 단계에 모두 적용했다. 기존 최고 성능은 zero-shot ImageNet에서 86.3%, fine-tuning에서는 91.0%(Yu et al., 2022)였다.

 

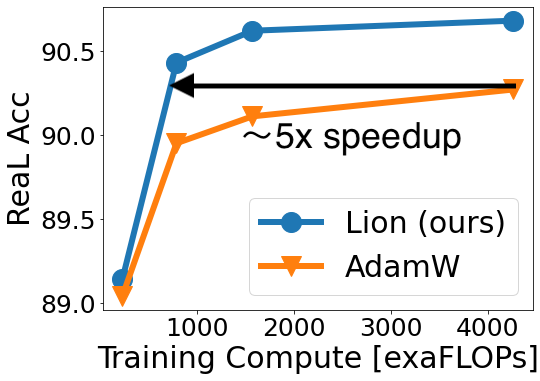
그림 1 설명:

• 왼쪽: JFT-300M에서 ViT 모델의 pre-training 연산량 대비 ImageNet fine-tuning 정확도
• 오른쪽: 해상도 256×256 이미지 생성을 위한 디퓨전 모델의 FID 점수
• 디코딩은 DDPM을 1K 스텝 동안 guidance 없이 수행함. 참고로 ADM의 FID는 10.94(Dhariwal and Nichol, 2021)

프로그램 1: 발견된 옵티마이저 Lion

기본값으로 β₁ = 0.9, β₂ = 0.99가 사용됨. 이 옵티마이저는 모멘텀만 추적하며, sign 연산으로 업데이트를 계산한다. 회색 줄은 decoupled weight decay를 계산하는 부분이며, λ는 weight decay 강도를 의미한다.

def train(weight, gradient, momentum, lr):
  update = interp(gradient, momentum, β₁)
  update = sign(update)
  momentum = interp(gradient, momentum, β₂)
  weight_decay = weight * λ
  update = update + weight_decay
  update = update * lr
  return update, momentum

 

최적화 알고리즘을 자동으로 발견하려는 또 다른 접근은 "Learning to Optimize (L2O)"이다. L2O는 파라미터화된 모델(예: 뉴럴 네트워크)을 학습시켜 업데이트를 출력하도록 한다(Andrychowicz et al., 2016; Metz et al., 2019; Li and Malik, 2017; Metz et al., 2022). 그러나 이러한 블랙박스 방식의 옵티마이저들은 보통 소규모 태스크에서 훈련되어 대규모 실제 문제로 일반화하는 데 어려움을 겪는다.

 

또 다른 접근법(Bello et al., 2017; Wang et al., 2022)은 강화학습이나 몬테카를로 샘플링을 통해 새로운 옵티마이저를 탐색한다. 이 방식에서는 gradient, momentum과 같은 predefined operand들과 수학 연산을 조합해 트리 구조의 탐색 공간을 구성한다. 하지만 탐색을 효율적으로 수행하기 위해, operand를 고정하거나 트리 크기를 제한하는 등 탐색 공간을 축소하게 되어 잠재적인 최적화를 놓치는 경우가 많다. 예를 들어, 이러한 방식은 momentum의 추적 방식이나 그것이 update에 기여하는 방식 등 Lion의 핵심 구조를 수정할 수 없다.

 

AutoML-Zero(Real et al., 2020)는 ML 파이프라인의 모든 구성 요소를 탐색 대상으로 삼는 도전적인 연구이다. 본 논문은 AutoML-Zero의 철학을 계승하면서도, 실제 SOTA 성능을 향상시킬 수 있는 실용적인 최적화 알고리즘을 발견하는 데 목적을 둔다.

 

본 논문에서는 알고리즘 발견 문제를 프로그램 탐색(program search)으로 공식화하고, 이를 최적화 알고리즘 탐색에 적용한다. 우리는 다음 두 가지 주요 과제를 다룬다:

1. 무한하고 희소한 프로그램 공간에서 고품질 알고리즘을 발견하는 것
2. 작은 프록시 태스크에서 잘 작동했던 알고리즘이 실제 SOTA 태스크로 일반화되도록 선택하는 것

이 문제를 해결하기 위해, 우리는 warm-start 및 restart 기반 진화 탐색, 추상 실행, funnel selection, 프로그램 단순화 등 다양한 기법을 활용한다.

 

우리가 발견한 최적화 알고리즘은 Lion (EvoLved Sign Momentum) 으로, 오직 momentum만을 추적하고 sign 연산을 통해 업데이트를 계산한다. 이 구조는 메모리 사용량을 줄이고, 모든 파라미터에 동일한 크기의 업데이트를 적용하게 한다. Lion은 구조는 단순하지만 다양한 모델(Transformer, MLP, ResNet, U-Net, Hybrid)과 태스크(image classification, contrastive learning, diffusion, language modeling, fine-tuning)에서 탁월한 성능을 보인다.

특히, BASIC (Pham et al., 2021) 모델에서 Adafactor 대신 Lion을 사용하면:

• ImageNet에서 Zero-shot 정확도 88.3%, Fine-tuning 정확도 91.1% 를 달성함
  (기존 최고 성능 대비 각각 2%, 0.1% 향상)
• JFT 사전학습 연산량을 최대 5배 절감
• 디퓨전 모델 학습 효율은 2.3배 향상, FID 점수도 개선
• 언어 모델링에서도 성능은 동일하거나 더 좋고, 연산량은 최대 2배 절감

우리는 Lion의 특성 및 한계점도 분석하였다.

• Sign 함수 기반 업데이트는 SGD나 adaptive 옵티마이저보다 큰 노름(norm) 을 가지므로,
  학습률은 더 작게, decoupled weight decay λ는 더 크게 설정해야 효과적인 정규화가 이루어진다. (자세한 내용은 5절 참고)
• Lion은 batch size가 클수록 더 효과적이며, AdamW보다 하이퍼파라미터 변화에 더 강건함
• 반면, 대규모 언어/이미지-텍스트 데이터셋에서는 AdamW와 통계적으로 유의미한 차이가 없을 수 있음
• 또한, 강한 augmentation이나 batch size가 64 미만일 때는 성능 차이가 작을 수 있음 (6절 참고)

프로그램 2: 일반적인 학습 루프 예시

train 함수 내부에 최적화 알고리즘이 구현되어 있음.
입력: 가중치 w, 그래디언트 g, 학습률 스케줄 lr
출력: 업데이트된 가중치

w = weight_initialize()
v1 = zero_initialize()
v2 = zero_initialize()
for i in range(num_train_steps):
  lr = learning_rate_schedule(i)
  g = compute_gradient(w, get_batch(i))
  update, v1, v2 = train(w, g, v1, v2, lr)
  w = w - update

 

프로그램 3: 초기 프로그램 (AdamW, 단순화를 위해 bias correction과 epsilon 생략)

def train(w, g, m, v, lr):
  g2 = square(g)
  m = interp(g, m, 0.9)
  v = interp(g2, v, 0.999)
  sqrt_v = sqrt(v)
  update = m / sqrt_v
  wd = w * 0.01
  update = update + wd
  lr = lr * 0.001
  update = update * lr
  return update, m, v

 

프로그램 4: 탐색, 선택, 정리 후 얻어진 최종 프로그램 (가독성을 위해 변수명을 일부 변경)

def train(w, g, m, v, lr):
  g = clip(g, lr)
  g = arcsin(g)
  m = interp(g, v, 0.899)
  m2 = m * m
  v = interp(g, m, 1.109)
  abs_m = sqrt(m2)
  update = m / abs_m
  wd = w * 0.4602
  update = update + wd
  lr = lr * 0.0002
  m = cosh(update)
  update = update * lr
  return update, m, v

 

2. 알고리즘의 기호적(Symbolic) 발견

우리는 알고리즘 발견 문제를 프로그램 탐색(program search)으로 공식화하는 접근을 제안한다(Koza, 1994; Brameier et al., 2007; Real et al., 2020). 이 과정에서 우리는 프로그램 형태의 기호적 표현(symbolic representation)을 사용하며, 이는 다음과 같은 장점을 지닌다:

1. 알고리즘은 결국 실행을 위해 프로그램으로 구현되어야 한다는 점에서, 프로그램 표현은 이와 잘 부합한다.
2. 뉴럴 네트워크와 같은 파라미터화된 모델에 비해, 프로그램과 같은 기호적 표현은 분석, 이해, 그리고 새로운 태스크로의 전이가 더 용이하다.
3. 프로그램의 길이를 통해 복잡도를 추정할 수 있어, 일반적으로 더 단순하고 더 잘 일반화되는 알고리즘을 선택하기 쉬워진다.

본 연구는 딥 뉴럴 네트워크 학습을 위한 옵티마이저를 주된 대상으로 하지만, 제안된 방법은 다른 과제들에도 일반적으로 적용 가능하다.

 

2.1 프로그램 탐색 공간 (Program Search Space)

우리는 프로그램 탐색 공간을 설계할 때 다음 세 가지 기준을 따랐다:

1. 새로운 알고리즘을 발견할 수 있을 정도로 유연한 탐색 공간이어야 한다.
2. 생성된 프로그램은 분석하기 쉽고, 머신러닝 워크플로우에 통합하기 쉬워야 한다.
3. 탐색 대상은 저수준 구현 세부사항이 아닌, 고수준 알고리즘 설계에 집중해야 한다.

우리는 프로그램을 n차원 배열에 작용하는 함수들로 정의하며, 리스트나 딕셔너리 같은 구조체도 배열을 포함할 수 있고, 이러한 프로그램은 명령형(imperative) 언어 형태로 표현된다. 이는 NumPy / JAX(Harris et al., 2020; Bradbury et al., 2018) 기반의 Python 코드 또는 최적화 알고리즘의 의사코드와 유사하다. 아래에서는 설계의 세부 사항을 설명하며, AdamW를 예시로 든 프로그램 표현은 Program LABEL:lst:p1에 제시되어 있다.

 

 

✅ 입력/출력 시그니처 (Input / Output Signature)

프로그램은 train 함수를 정의하며, 이는 탐색 대상이 되는 최적화 알고리즘을 구현하는 부분이다.

• 입력: 모델 가중치 w, 그래디언트 g, 현재 step에서의 학습률 스케줄 값 lr
• 출력: 가중치 업데이트 update
• 보조 변수: 학습 중 과거 정보를 저장하기 위한 0으로 초기화된 변수들 (예: AdamW는 1차, 2차 모멘트를 추정하기 위해 m, v를 사용)

이러한 변수들은 자유롭게 사용할 수 있으며, 가독성을 위해 Program LABEL:lst:p1에서는 m, v라는 이름을 사용했다.
또한, Program LABEL:loop의 단순화된 코드 스니펫은 AdamW와 동일한 시그니처를 사용하여, 발견된 알고리즘이 동일하거나 더 적은 메모리 사용량을 갖도록 설계되었다.

 

이전의 옵티마이저 탐색 연구(Bello et al., 2017; Wang et al., 2022)와 달리, 우리는 보조 변수 업데이트 방식을 새롭게 발견하는 것도 허용한다.

 

🧱 빌딩 블록 (Building Blocks)

train 함수는 할당문(statement) 들의 연속으로 구성되며,

• 문장의 개수나 로컬 변수 수에는 제한이 없다.
• 각 문장은 상수 혹은 기존 변수를 입력으로 하여 함수 하나를 호출하고, 그 결과를 새로운 변수 혹은 기존 변수에 저장한다.

우리는 NumPy나 선형대수 연산에서 자주 쓰이는 45개의 수학 함수를 선택해 사용했다.

• 예: 선형 보간 함수 interp(x, y, a)는 (1 - a) * x + a * y로 정의
• 조건문, 반복문, 사용자 정의 함수 등 고급 기능도 실험해봤지만, 성능 향상은 없어 제외함
• 각 함수의 타입과 shape은 필요 시 자동으로 변환됨 (예: 배열 딕셔너리 + 스칼라 연산)

각 함수에 대한 자세한 설명은 부록 H(Appendix H)에 정리되어 있다.

 

🔁 변이(Mutations)와 중복 문장(Redundant Statements)

진화 탐색(evolutionary search)에서 사용되는 변이는 프로그램 표현 방식과 밀접하게 연관된다.
우리는 다음 세 가지 유형의 변이를 포함한다:

1. 새 문장 삽입: 무작위 위치에 함수 및 인자를 무작위로 선택해 새 문장을 추가
2. 문장 삭제: 기존 문장 중 하나를 삭제
3. 문장 수정: 임의의 문장의 인자(변수 또는 상수)를 무작위로 수정

상수를 변이할 경우 다음과 같이 설정함:

• 정규분포에서 샘플링된 상수로 대체 (X ~ 𝒩(0, 1))
• 기존 상수에 2^a를 곱함 (a ~ 𝒩(0, 1))

이러한 상수는 옵티마이저의 하이퍼파라미터(예: learning rate, weight decay) 역할을 한다.

 

☑️ 또한, 탐색 중에는 출력에 영향을 미치지 않는 중복 문장도 허용한다. 이는 단일 문장만 변이 가능하기 때문에, 미래에 유의미한 구조 변경을 만들기 위한 중간 단계로서 필요하다.

 

♾️ 무한하고 희소한 탐색 공간 (Infinite and Sparse Search Space)

• 문장 수, 변수 수, 상수가 무한하므로 탐색 공간은 본질적으로 무한대이다.
• 상수를 무시하고 문장 길이와 변수 수를 제한한다 해도, 가능한 프로그램 수는 매우 방대하다.

하지만 진짜 어려운 점은, 이 거대한 공간에서 성능이 좋은 프로그램이 매우 희소하다는 데 있다.

 

이를 보여주기 위해, 우리는 저비용 proxy task에서 무작위로 생성한 200만 개의 프로그램을 평가했고, 가장 성능이 좋은 프로그램조차 AdamW보다 훨씬 낮은 성능을 보였다.

 

📊 그림 2 설명

왼쪽:

• AdamW와 무작위 탐색(random search)에 대해 4배 더 많은 연산량으로 하이퍼파라미터 튜닝을 수행한 결과를 baseline으로 설정 (초록색, 빨간색 선)
• 우리의 진화 탐색(evolutionary search)은 5회 반복 평균 및 표준편차를 기준으로 baseline들을 크게 상회함
• 초기 프로그램에서 여러 번 재시작하는 것이 중요하며,
  30만 스텝 후 최고 프로그램에서 재시작하면, 정체된 탐색을 극복하고 성능이 더 향상됨 (주황색 곡선)

오른쪽:

• 탐색 성능(fitness), 캐시 적중률(cache hit rate), 중복 문장 비율의 예시 그래프
• 탐색이 진행됨에 따라 캐시 적중률은 약 90%, 중복 문장 비율은 약 70%까지 증가함

 

2.2 효율적인 탐색 기법 (Efficient Search Techniques)

우리는 무한하고 희소한 탐색 공간이 가지는 문제를 해결하기 위해 다음과 같은 기법들을 적용하였다.

 

🌱 Warm-start 및 재시작을 활용한 진화 탐색

우리는 정규화된 진화(regularized evolution) 알고리즘을 활용하는데, 이는 단순하고 확장 가능하며 다양한 AutoML 탐색 과제에서 성공적으로 활용되어 왔다(Real et al., 2020, 2019; Ying et al., 2019; So et al., 2019; Holland, 1992).

• 이 방식은 크기 P의 알고리즘 집단(population)을 유지하며 반복적으로 개선해 나간다.
• 각 반복(cycle)마다 T<P개의 알고리즘을 무작위로 선택하고, 그 중 성능이 가장 우수한 것을 부모(parent)로 선택한다 (tournament selection, Goldberg and Deb, 1991).
• 이 부모 알고리즘은 복사되고 변이되어 새로운 자식 알고리즘이 생성되며, 이 자식은 집단에 추가되고 가장 오래된 알고리즘은 제거된다.

보통 진화 탐색은 무작위 초기 개체로 시작하지만, 우리는 탐색 속도를 높이기 위해 초기 집단을 AdamW로 warm-start한다. 기본 설정은 tournament 크기 2, 집단 크기 1000이다.

 

탐색 효율을 더욱 높이기 위해 두 가지 유형의 재시작 전략을 적용하였다:

1. 초기 프로그램으로부터 재시작
   • 진화 탐색의 랜덤성 때문에 서로 다른 로컬 옵티마를 찾을 수 있어, 탐색 다양성을 증가시킴
   • 병렬 탐색을 통해 구현 가능
2. 현재까지 발견된 최적 알고리즘으로부터 재시작
   • 더 나은 최적화를 유도하며, 탐색 수렴 후의 성능 향상에 도움

▶ 그림 2(왼쪽)는 5회 반복된 진화 탐색의 평균과 표준 오차를 보여준다.
우리는 AdamW를 기반으로 하이퍼파라미터 튜닝을 수행(상수만 변이 허용), 또는 무작위 프로그램을 샘플링한 random search를 4배 더 많은 연산량으로 실행하였으며, 우리의 탐색은 이 두 baseline 결과(점선) 모두를 크게 능가하였다.

 

탐색 fitness의 분산이 크므로, 여러 번 반복 및 초기화 기반 재시작이 필수이다. 탐색 fitness가 약 30만 스텝 이후 정체되면, 지금까지 발견된 최고 프로그램으로부터 재시작 시 fitness가 추가로 향상됨 (주황색 곡선 참고).

 

✂️ 추상 실행 기반의 가지치기 (Pruning through Abstract Execution)

우리는 프로그램 공간의 중복성을 제거하기 위해 세 가지 원천을 고려한다:

1. 문법 오류, 타입/shape 오류가 있는 프로그램
2. 기능적으로 동일한(semantically duplicate) 프로그램
3. 출력에 영향을 미치지 않는 중복 문장

실제 실행에 앞서, 우리는 추상 실행(abstract execution) 단계를 수행하여:

1. 변수 타입과 shape을 추론해 오류 있는 프로그램을 제거하며, 유효한 자식이 생성될 때까지 부모를 반복적으로 변이시킴
2. 입력으로부터 출력이 계산되는 방식에 대한 고유한 해시(hash)를 생성하여, 기능적으로 동일한 프로그램을 캐시에서 식별 및 재사용
3. 중복 문장을 탐지 및 제거하여 실행 및 분석 시 무시

예를 들어, Program LABEL:lst:p2는 Program LABEL:lst:raw에서 모든 중복 문장을 제거하여 얻어진 것이다.

 

추상 실행은 실제 실행 대비 비용이 매우 낮으며, 각 입력/함수는 해시 등으로 대체된다. 세부 구현은 부록 I(Appendix I)에 설명되어 있다.

 

예비 실험에서는 유효하지 않은 프로그램이 너무 많을 경우 탐색이 정체됨을 확인하였으며, 이 때문에 유효성 필터링이 필수적임을 확인했다.

▶ 그림 2(오른쪽)에서, 탐색이 진행됨에 따라 중복 문장 비율과 캐시 적중률이 증가하는 것을 볼 수 있다.

• 5번의 탐색에서 평균적으로 69.8% ± 1.9%의 문장이 중복되었고,
  → 중복 제거 시 프로그램이 약 3배 더 짧아짐 → 분석 및 평가가 더 쉬워짐
• 캐시 적중률은 89.1% ± 0.6%,
  → 이는 캐시(Hash Table)를 사용함으로써 탐색 비용을 약 10배 절감함을 의미

⚙️ 프록시 태스크 및 탐색 비용 (Proxy Tasks and Search Cost)

탐색 비용을 줄이기 위해, 우리는 모델 크기, 학습 예제 수, 스텝 수를 줄인 프록시(proxy) 태스크를 설계하였다.

• 프록시 평가 1회는 TPU V2 1칩에서 약 20분 이내에 완료 가능
• validation set의 정확도 또는 perplexity를 fitness로 사용

각 탐색 실험은 TPU V2 100개를 사용하며, 약 72시간 동안 실행된다.

• 총 생성 프로그램 수: 20~30만 개
• 이 중 실제로 평가되는 수는 2~3만 개 수준으로, 이는 캐시를 통한 중복 제거 덕분

재시작을 포함하기 위해, 우리는

• 5회 반복 탐색을 실행하고,
• 이후 지금까지 발견된 최고 알고리즘으로부터 초기화한 추가 탐색을 수행한다.
  → 총 연산량은 약 3,000 TPU V2-days에 해당한다.
  (프록시 태스크 상세 내용은 부록 F 참고)

📈 그림 3 설명

왼쪽:

• Section 2.3에서 정의하는 meta-validation 태스크에서의 성능 곡선
• 프록시보다 약 500배 더 큰 평가 태스크를 사용
• 파란 곡선: 탐색 초반 15%에서 meta-overfitting 발생
• 주황 곡선: 탐색의 약 90%까지 유지되며 더 나은 성능 달성
  → 나중에 overfit하는 쪽이 일반화 성능이 더 좋음

오른쪽:

• 50회 탐색에서 meta-overfitting이 발생한 시점의 히스토그램
• 절반은 초기에 overfit하지만, 상당수는 후반부까지 일반화 유지
• 각 구간의 평균 meta-validation 성능은 나중에 overfit한 경우가 더 높음

 

2.3 일반화: 프로그램 선택 및 단순화

(Generalization: Program Selection and Simplification) 탐색 실험을 통해 프록시 태스크에서 유망한 프로그램을 발견할 수 있다. 그러나 우리는 이들 중 프록시 태스크를 넘어 일반화(generalization) 되는 알고리즘을 선택하고, 이후 이를 단순화(simplification) 한다. 이를 위해, 프록시보다 더 큰 meta-validation 태스크를 정의하는데, 여기서는 모델 크기와 학습 스텝 수를 늘려 평가한다.

• 이러한 과정에서 발생할 수 있는 현상이 메타 오버피팅(meta-overfitting)이다.
  → 이는 탐색 과정의 fitness는 계속 상승하지만, meta-validation 성능은 떨어지는 현상으로, 발견된 알고리즘이 프록시 태스크에 과적합되었음을 의미한다.
  → 그림 3(왼쪽)에서 그 예시를 보여주며, 파란 곡선은 초기 meta-overfitting, 주황 곡선은 후기 meta-overfitting 사례를 나타낸다.

⚠️ 큰 일반화 격차 (Large Generalization Gap)

발견된 알고리즘은 프록시 태스크와 실제 목표(target) 태스크 사이에 존재하는 상당한 일반화 격차(generalization gap)라는 도전 과제에 직면한다.

• 프록시 태스크는 TPU V2 칩 하나에서 20분 이내에 학습 완료될 수 있지만,
• 실제 타겟 태스크는 10⁴배 이상 더 크며, TPU V4 512개로 수일간 학습이 필요할 수 있다.
• 또한, 우리는 옵티마이저가 다양한 모델 구조, 데이터셋, 심지어는 도메인까지도 잘 작동하길 기대하기 때문에,
  → 탐색된 알고리즘은 강력한 분포 외 일반화(out-of-distribution generalization) 능력을 가져야 한다.

하지만 탐색 공간의 희소성과 진화 과정에 존재하는 노이즈는 이 과제를 더욱 어렵게 만들며, 탐색 반복(run)마다 일반화 성능이 일관되지 않게 되는 경향이 있다.

 

우리는 실험을 통해, meta-overfitting이 늦게 발생한 탐색일수록 더 잘 일반화되는 알고리즘을 발견할 가능성이 높다는 것을 관찰하였다 (그림 3 오른쪽 참조).

 

🔽 깔때기 선택(Funnel Selection)

일반화 문제를 완화하기 위해, 우리는 탐색 fitness 기준으로 유망한 프로그램을 수집하고, 여러 meta-validation 태스크를 활용한 추가적인 선택 단계를 거친다. 이를 효율적으로 수행하기 위해 깔때기(funnel) 방식의 선택 프로세스를 적용한다:

• 작은 프록시 태스크 A에서 시작해,
• 모델 크기와 학습 스텝을 늘려 10배 큰 태스크 B 생성
• 여기서 baseline을 능가하는 알고리즘만 더 큰 100배 규모의 태스크 C로 이동

이러한 방식은 일반화 성능이 낮은 알고리즘을 점진적으로 걸러내고, 최종적으로 대규모 태스크에도 일반화되는 알고리즘을 선택할 수 있도록 돕는다.

 

🧹 단순화 (Simplification)

단순한 프로그램은 이해하기 쉬울 뿐만 아니라, 일반화 가능성도 더 높을 것이라는 직관에 따라 다음의 과정을 통해 프로그램을 단순화한다:

1. 중복 문장 제거
   • 추상 실행(abstract execution)을 통해 최종 출력에 영향을 미치지 않는 문장을 식별하고 제거
2. 효과가 미미한 문장 제거
   • 중복은 아니지만, 제거했을 때 출력에 거의 영향을 주지 않는 문장을 제거
   • 이 과정은 진화 탐색 중 새 문장을 삽입하지 않도록 설정해 자동화할 수도 있음
3. 코드 정리 및 명확화
   • 문장을 재배치하고,
   • 변수 이름을 명확하고 설명적으로 수정하며,
   • 수학적으로 동등한 더 단순한 형태로 프로그램을 재작성

3. Lion의 도출 및 분석

(Derivation and Analysis of Lion) 우리는 Lion 옵티마이저를 그 단순성, 메모리 효율성, 그리고 탐색 및 메타-검증에서의 강력한 성능 때문에 선택하게 되었다. 또한, 탐색 과정에서는 기존 알고리즘 또는 새로운 알고리즘들도 함께 발견되었으며, 이들 중 일부는 더 나은 정규화를 제공하거나, AdaBelief(Zhuang et al., 2020) 또는 AdaGrad(Duchi et al., 2011)와 유사한 형태를 띠는 경우도 있었다 (자세한 내용은 부록 D(Appendix D) 참조).

 

3.1 도출 (Derivation)

탐색 및 깔때기 선택(funnel selection) 과정을 통해 우리는 Program LABEL:lst:p2에 도달하게 되며, 이 코드는 부록(Appendix)에 제시된 원시 프로그램(raw Program LABEL:lst:raw)에서 불필요한 문장을 자동으로 제거하여 얻어진 것이다.

 

우리는 이를 추가적으로 단순화하여 최종 알고리즘(Lion)을 Program LABEL:lst:p0에 제시하였다. 단순화 과정에서 여러 불필요한 요소들이 제거되었다:

• cosh 함수는 제거되었는데, 이는 변수 m이 다음 반복에서 다시 할당되기 때문이며 (3번째 줄 참조)
• arcsin과 clip을 사용하는 문장도 제거되었는데, 성능 저하 없이 생략 가능함을 관찰했기 때문이다
• 빨간색으로 표시된 세 개의 문장은 하나의 sign 함수로 축약될 수 있다

또한 Program LABEL:lst:p2에서는 m과 v가 모두 사용되지만,

• 사실 v는 단지 momentum(m) 업데이트 방식에만 영향을 주며,
• 두 개의 interp 함수에 각각 약 0.9와 1.1이라는 상수를 사용한 것은 단일 interp 함수에 0.99를 사용하는 것과 동등하므로
  → v는 따로 추적할 필요가 없다

또한, bias correction은 방향을 바꾸지 않기 때문에 더 이상 필요하지 않다. 최종 알고리즘은 Algorithm 2에 의사코드(pseudocode)로 제시되어 있다.

 

3.2 분석 (Analysis)

🔁 Sign 업데이트와 정규화 효과

Lion 알고리즘은 sign 연산을 통해 모든 차원에 대해 동일한 크기의 업데이트를 생성하며, 이는 다양한 적응형(adaptive) 옵티마이저들과 본질적으로 다른 방식이다. 직관적으로 볼 때, sign 연산은 업데이트에 노이즈를 추가하게 되며, 이것이 일종의 정규화 효과를 유발하고, 일반화 성능을 향상시키는 데 도움이 된다 (Neelakantan et al., 2017; Foret et al., 2021; Chen et al., 2022 참조).

그 근거로, 부록의 그림 11(오른쪽)에서는 다음과 같은 결과가 제시되어 있다:

• ImageNet에서 Lion으로 학습된 ViT-B/16 모델은
  → AdamW보다 학습 오류(training error)는 더 크지만,
  → 검증 정확도(validation accuracy)는 2% 더 높다 (표 2 참조)

또한, 부록 G의 결과는 Lion이 보다 부드러운(loss surface가 완만한) 영역으로의 수렴을 유도함을 보여주며, 이는 일반적으로 더 나은 일반화 성능으로 이어지는 것으로 알려져 있다.

 

🔄 모멘텀 추적 (Momentum Tracking)

Lion에서 모멘텀을 추적하기 위해 사용하는 기본 지수이동평균(EMA) 계수는 0.99(β₂)이며, 이는 AdamW나 Momentum SGD에서 일반적으로 사용하는 0.9보다 높다. 업데이트를 적용하기 전에는 현재 gradient와 기존 momentum을 0.9(β₁)의 비율로 보간(interpolation)한다. 이러한 EMA 계수와 보간 방식의 조합은 다음의 균형을 가능하게 한다:

• 모멘텀 내에 gradient의 약 10배 더 긴 이력(history)을 유지하면서도,
• 현재 gradient에 더 큰 가중치를 부여하는 업데이트 수행

β₁과 β₂의 필요성에 대해서는 4.6절에서 더 자세히 논의한다.

 

⚙️ 하이퍼파라미터 및 배치 사이즈 선택 (Hyperparameter and Batch Size Choices)

Lion은 AdamW나 Adafactor에 비해 구조가 더 단순하며,

• ε나 factorization 관련 하이퍼파라미터가 필요 없다.

weight decay 항을 생략한다면, Lion의 업데이트는 ±1의 이진(binary) 값으로 구성된 요소별 연산(element-wise)이 된다.
→ 이는 SGD나 적응형 옵티마이저들이 생성하는 업데이트보다 노름(norm)이 더 크다.

이로 인해, Lion은 다음과 같은 세팅이 필요하다:

• 더 작은 학습률(learning rate)
• 그에 상응하는 더 큰 decoupled weight decay
  → 그래야 lr × λ로 나타나는 실질적인 weight decay 강도가 다른 옵티마이저와 유사해진다.

Lion의 튜닝에 대한 자세한 내용은 5절에서 다룬다. 또한, Lion은 batch size가 커질수록 AdamW보다 성능 이점이 더 커지며, 이는 모델 학습을 데이터 병렬화로 확장하는 일반적인 실무 관행과 잘 부합한다 (4.6절 참조).

 

💾 메모리 및 실행 속도 측면의 이점 (Memory and Runtime Benefits)

Lion은 모멘텀만 저장하므로, AdamW와 같은 인기 있는 적응형 옵티마이저보다 메모리 사용량이 적다.
→ 이는 대규모 모델 학습이나 큰 batch size를 사용할 때 특히 유리하다.

예를 들어:

• AdamW는 ViT-B/16 (해상도 224, batch size 4096)을 학습하는 데 최소 16개의 TPU V4 칩이 필요하지만,
• Lion은 동일 조건에서 단 8개만으로 충분하다 (두 경우 모두 bfloat16 모멘텀 사용 시)

또 다른 실용적 장점은 Lion의 단순함으로 인해 실행 속도(steps/sec)가 더 빠르다는 점이다.
→ 작업, 코드베이스, 하드웨어에 따라 AdamW 및 Adafactor 대비 2~15% 속도 향상이 관찰되었다.

 

🔗 기존 옵티마이저와의 관계 (Relation to Existing Optimizers)

sign 연산은 과거 여러 옵티마이저에서도 사용된 바 있다 (Riedmiller and Braun, 1993; Bernstein et al., 2018).

그중 Lion과 가장 유사한 알고리즘은 hand-crafted 방식의 signSGD(Bernstein et al., 2018) 및 그 모멘텀 버전이다.
→ 이들 또한 sign 연산으로 업데이트를 계산하지만,
→ 모멘텀 업데이트 방식은 Lion과 다르다.

signSGD는 분산 학습 환경에서 통신 비용을 줄이는 것에 중점을 두며,
→ ConvNet을 사용한 이미지 분류 성능은 낮은 편이라고 보고되었다.

또한, NAdam(Dozat, 2016)은 업데이트된 1차 모멘텀과 gradient를 결합해 업데이트를 계산하는 반면, Lion은 모멘텀 추적과 그것의 적용을 β₂를 통해 분리(decouple)한다. Lion과 관련된 옵티마이저들의 비교는 4.5절에서 다룬다.

 

4. Lion의 성능 평가

(Evaluation of Lion) 이 절에서는 다양한 벤치마크에서 Lion 옵티마이저의 성능 평가 결과를 제시한다. 우리는 주로 AdamW(또는 메모리가 병목인 경우 Adafactor)와 비교한다.
→ 이들은 대부분의 학습 과제에서 널리 사용되며 사실상의 표준 옵티마이저이기 때문이다.

Momentum SGD는 ResNet에 대해서만 결과를 포함하였으며,
→ 다른 모델에서는 성능이 AdamW보다 낮기 때문이다.

4.5절에서는 hand-crafted 및 자동 탐색 기반의 다른 인기 있는 옵티마이저들도 벤치마크 비교에 포함하였다. 우리는 모든 옵티마이저가 각 과제에 대해 충분히 튜닝되었음을 보장하였다 (튜닝 세부 사항은 5절 참고).

기본적으로 다음과 같은 설정을 사용하였다:

• Learning rate 스케줄: cosine decay
• Warmup 스텝 수: 10,000
• Momentum 저장 형식: bfloat16 (메모리 사용량 감소 목적)

📊 표 2: ImageNet, ImageNet ReaL, ImageNet V2에서의 정확도

• 괄호 안의 수치 (⋅)는 Dai et al. (2021), Dosovitskiy et al. (2021)에서 인용한 값이다.
• 모든 결과는 3회 실행 평균값으로 보고되었다.

 

4.1 이미지 분류 (Image Classification)

우리는 이미지 분류 과제에서 다양한 데이터셋과 모델 구조를 대상으로 실험을 수행하였다 (데이터셋 세부사항은 부록 B 참고).
ImageNet에서의 scratch 학습뿐 아니라, 더 큰 규모의 대표적인 데이터셋인 ImageNet-21K와 JFT(Sun et al., 2017)에서의 사전학습(pre-training)도 수행하였다. 기본 이미지 크기는 224×224이며, 별도로 명시되지 않으면 이 크기를 사용한다.

 

🏁 ImageNet에서 Scratch 학습

기존 연구들(Dosovitskiy et al., 2021; He et al., 2016)을 따라,

• ResNet-50은 90 epoch 동안 batch size 1,024로 학습
• 나머지 모델들은 300 epoch 동안 batch size 4,096으로 학습하였다

표 2에 나타난 바와 같이, Lion은 다양한 모델 구조에서 AdamW를 명확히 상회한다. 특히, 모델 용량이 클수록 성능 향상이 더욱 뚜렷하게 나타나며, 예를 들어 ViT-B/16과 ViT-S/16의 경우 정확도가 각각 +1.96%, +0.58% 증가하였다. 또한 inductive bias가 적을수록 성능 차이가 더 벌어지는 경향이 있으며, 강력한 augmentation을 적용한 경우에도 Lion은 여전히 성능 우위를 보인다.
예: CoAtNet-3에서는 학습 시 강한 정규화(Dai et al., 2021)를 적용했음에도 불구하고, Lion이 AdamW보다 0.42% 더 높은 정확도를 달성하였다.

 

🧠 ImageNet-21K에서 사전학습 (Pre-train)

우리는 ViT-B/16과 ViT-L/16을 ImageNet-21K에서 batch size 4,096, 90 epoch으로 사전학습시켰다. 표 2에 따르면, 훈련 데이터가 10배로 증가했음에도 Lion은 여전히 AdamW보다 뛰어난 성능을 보인다.특히 큰 모델일수록 격차가 더 커지는데,

예를 들어:

• ViT-L/16:
  • ImageNet: +0.52%,
  • ReaL: +0.57%,
  • V2: +0.74%
• ViT-B/16:
  • 각각 +0.33%, +0.23%, +0.25%

🚀 JFT에서 사전학습 (Pre-train on JFT)

한계를 확장하기 위해, 우리는 JFT에서 대규모 실험을 수행하였다. 사전학습 및 파인튜닝 설정은 Dosovitskiy et al. (2021), Zhai et al. (2021)의 실험을 따랐다. 그림 1(왼쪽) 및 그림 4는 JFT-300M에서 사전학습된 세 가지 ViT 모델 (ViT-B/16, ViT-L/16, ViT-H/14)의 성능을 사전학습 연산량별로 비교한 것이다. Lion은 다음과 같은 결과를 달성하였다:

• ViT-L/16이, AdamW로 학습된 ViT-H/14와 ImageNet 및 V2에서 동등한 성능을 내지만,
  → 사전학습 연산량은 1/3 수준
• ImageNet ReaL에서는 5배 더 적은 연산량으로도 동일 성능 달성

또한, Zhai et al. (2021)이 AdamW로 ViT-L/16을 400만 스텝 학습했을 때보다, 우리는 Lion으로 100만 스텝만에 더 나은 성능을 얻었다.

 

🧪 표 3: JFT 사전학습 후 ImageNet 파인튜닝 성능

• 큰 모델 두 개는 JFT-3B,
• 작은 모델들은 JFT-300M에서 사전학습되었음
• ViT-G/14 결과는 Zhai et al. (2021)에서 인용
• ⋆ 주의: fine-tuning 과정에서 overfitting이 확인되어, 최종 결과와 Oracle 결과 모두 보고

표 3에서, Lion으로 학습된 ViT-L/16은 AdamW로 학습된 ViT-H/14와 동일한 성능을 달성하였고,
→ 모델 크기는 2배 작음

더 어려운 벤치마크에서는 이점이 더 커짐:

• ViT-L/16 기준
  • V2: +1.33%
  • A: +6.08%
  • R: +5.54%

JFT-3B로 확장 시,

• Lion으로 학습한 ViT-G/14는
  → Zhai et al. (2021)의 기존 ViT-G/14보다 더 적은 파라미터(1.8배 감소)로도 더 나은 성능을 보였으며,
  → ImageNet 정확도 90.71%를 달성하였다.

📈 그림 4:

JFT-300M 사전학습 후 ImageNet 파인튜닝 성능

• 왼쪽: ImageNet ReaL 정확도
• 오른쪽: ImageNet V2 정확도
  → 자세한 수치는 부록의 표 8 참고

 

🟦 표 4: LiT의 Zero-shot 정확도

• 대상: ImageNet, CIFAR-100, Oxford-IIIT Pet
• 참고로, CLIP(Radford et al., 2021)의 ImageNet zero-shot 정확도는 76.2%임

4.2 비전-언어 대조 학습

(Vision-Language Contrastive Learning) 이 절에서는 비전-언어 대조 학습(Radford et al., 2021)에 초점을 맞춘다.
우리는 zero-shot 이미지 분류 및 이미지-텍스트 검색 벤치마크에서 Lion과 AdamW (또는 Adafactor)를 비교한다.

모든 파라미터를 처음부터 학습하는 대신, 이미지 인코더는 강력한 사전학습 모델로 초기화하는데, 이는 더 효율적이라는 연구(Zhai et al., 2022)를 따른 것이다.

 

🔒 Locked-image Text Tuning (LiT)

우리는 Zhai et al. (2022)의 방식에 따라, 동일한 frozen 사전학습된 ViT를 사용하고 텍스트 인코더만 대조 방식으로 학습하면서 Lion과 AdamW를 비교하였다.

• 학습 데이터: 10억 쌍의 이미지-텍스트 페어
• 배치 크기: 16,384

표 4는 세 가지 모델 크기에서의 zero-shot ImageNet 분류 결과를 보여준다. 모델 이름은 크기를 나타내며, 예를 들어 LiT-B/16-B는 ViT-B/16과 base 크기 텍스트 인코더를 의미한다. Lion은 다음과 같은 일관된 정확도 향상을 보였다:

• LiT-B/32-B: +1.10%
• LiT-B/16-B: +1.13%
• LiT-g/14288-L: +0.66%

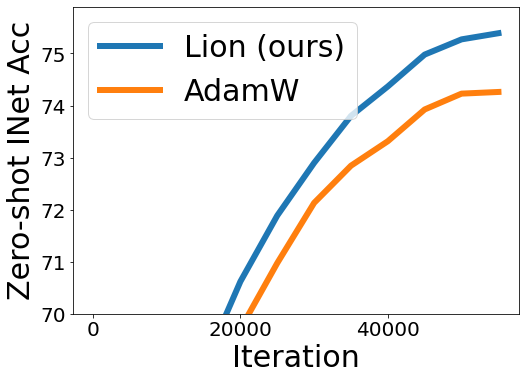
그림 5(왼쪽)에는 LiT-B/16-B의 zero-shot 학습 곡선이 예시로 제시되어 있다. 다른 두 데이터셋에서도 유사한 결과를 얻었다.

 

📊 이미지-텍스트 검색 성능

• MSCOCO(Lin et al., 2014)
• Flickr30K(Plummer et al., 2015)

→ 두 벤치마크의 결과는 부록의 그림 9에 제시되어 있다.

• 평가 지표: Recall@K
  → 쿼리의 정답 라벨이 top-K 결과 내에 포함되었는지 여부를 기준으로 평가

Lion은 두 데이터셋 모두에서 AdamW보다 뛰어난 성능을 보였으며, 특히 Flickr30K에서는 Recall@1에서의 향상 폭이 Recall@10보다 더 큼
→ 이는 보다 정확한 검색 결과를 의미

• Image → Text: +1.70% (Recall@1) vs. +0.60% (Recall@10)
• Text → Image: +2.14% vs. +0.20%

🧠 BASIC

Pham et al. (2021)은 배치 크기, 데이터셋, 모델 크기를 동시에 확장하여, CLIP보다 훨씬 향상된 성능을 달성하였다.

• 이미지 인코더로는 JFT-5B에서 사전학습된 정교한 CoAtNet(Dai et al., 2021)을 사용
• 대조 학습은 66억 쌍의 이미지-텍스트에 대해 배치 크기 65,536으로 수행

우리는 성능 한계를 실험하기 위해 가장 큰 BASIC-L 모델만을 대상으로, 이미지 인코더 사전학습과 대조 학습 모두에 Lion을 적용하였다.

표 1에서 보듯,

• zero-shot ImageNet 분류 정확도는 88.3%로, 기준 모델보다 2.6% 향상되었으며
• 이는 이전 최고 성능(Yu et al., 2022)보다도 2.0% 높은 수치

또한, 다섯 가지 강인성 벤치마크에서도 일관된 성능 향상이 나타났다. CoAtNet-7을 사용하는 BASIC-L의 이미지 인코더를 fine-tuning한 결과,

• ImageNet Top-1 정확도는 91.1%를 달성했고,
• 이는 이전 SOTA보다 0.1% 더 높은 수치이다.

📉 그림 5

• 왼쪽: LiT-B/16-B의 zero-shot ImageNet 정확도 곡선
• 가운데 & 오른쪽:
  • 디퓨전 모델 학습 시, 64×64 및 128×128 이미지 생성에서의 FID 비교
  • guidance 없이 이미지 디코딩 수행

4.3 디퓨전 모델

(Diffusion Model) 최근 들어 디퓨전 모델은 이미지 생성 분야에서 압도적인 성공을 거두고 있다(Ho et al., 2020; Song et al., 2021; Dhariwal and Nichol, 2021; Ho and Salimans, 2022; Saharia et al., 2022). 이러한 막대한 가능성을 고려하여, 우리는 무조건적 이미지 생성(unconditional image synthesis)과 텍스트-조건 이미지 생성(multimodal text-to-image generation)에서 Lion의 성능을 평가하였다.

 

🖼️ ImageNet에서의 이미지 생성

우리는 Dhariwal and Nichol (2021)에서 제안된 개선된 U-Net 아키텍처를 활용하여, ImageNet에서 해상도 64×64, 128×128, 256×256의 이미지 생성을 수행하였다.

• 배치 크기: 2,048
• 학습률: 훈련 내내 고정

이미지 디코딩은 DDPM(Ho et al., 2020)을 사용하여 1,000 스텝 동안 classifier-free guidance 없이 샘플링을 수행하였다.
→ 평가지표로는 표준 FID 점수를 사용

그림 1(오른쪽)과 그림 5(가운데 및 오른쪽)에서 볼 수 있듯, Lion은 더 나은 FID 품질과 더 빠른 수렴 속도를 보여준다.

특히, 이미지 해상도가 높아질수록 과제가 더 어려워짐에 따라
→ Lion과 AdamW의 성능 차이도 더 커지는 경향이 있다.

예를 들어, 256×256 이미지 생성 시,

• Lion은 AdamW의 최종 성능을 44만 스텝이 아닌 약 19만 스텝 만에 달성하여
  → 2.3배의 학습 횟수 절감을 보였다.
• 최종 FID 점수:
  • Lion: 4.1
  • AdamW: 4.7
  • 참고로, ADM(Dhariwal and Nichol, 2021)의 FID는 10.94

✍️ 텍스트-조건 이미지 생성 (Text-to-Image Generation)

우리는 Imagen(Saharia et al., 2022)의 설정을 따라 다음 두 가지 모델을 훈련하였다:

1. 64×64 텍스트-조건 이미지 생성 모델 (base model)
2. 64×64 → 256×256 초해상도(super-resolution) 모델

• 훈련 데이터: 고품질의 내부 이미지-텍스트 데이터셋
• 배치 크기: 2,048
• 학습률: 고정

연산 자원의 제약으로 인해, base U-Net은 원래 20억 파라미터 모델에서 사용된 너비 512 대신 너비 192로 축소되었으며,
→ 600M 초해상도 모델은 원본 Imagen 구조와 동일하다.

훈련 중에는 MSCOCO(Lin et al., 2014) 검증 세트에서 2,000개의 이미지를 샘플링하여 실시간 평가를 수행하였다.

• CLIP score: 이미지-텍스트 정렬 정도 평가
• zero-shot FID-30K: 이미지의 충실도(fidelity) 평가

또한, 이미지-텍스트 정렬을 향상시킨다고 알려진
→ classifier-free guidance (Ho and Salimans, 2022)를 가중치 5.0으로 적용하였다.

그림 7은 학습 곡선을 보여준다.

• base 64×64 모델에서는 성능 향상이 명확하지 않지만,
• 텍스트 조건 초해상도 모델에서는 Lion이 AdamW보다 뛰어난 성능을 보여준다.
  • CLIP 점수는 더 높았고
  • FID는 더 적은 노이즈와 더 일관된 결과를 보였다.

그림 6:

• 왼쪽: Imagen 텍스트-투-이미지 64×64 모델 평가
• 오른쪽: 64×64 → 256×256 디퓨전 모델 평가

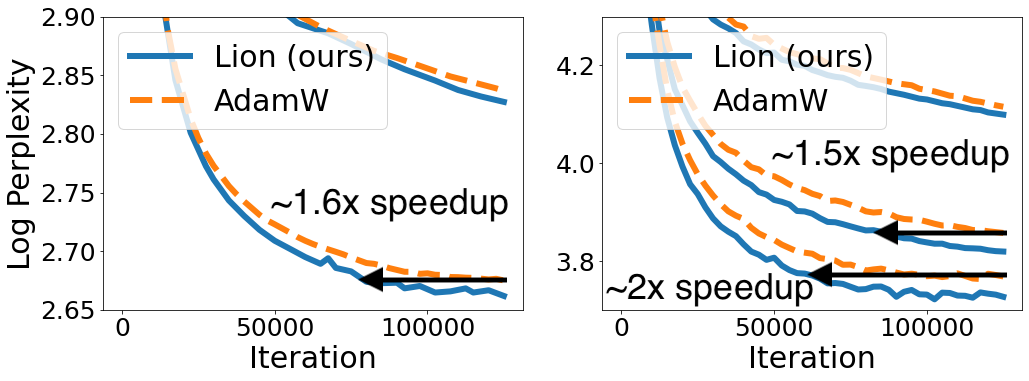
그림 7:

• 왼쪽: Wiki-40B에서의 로그 퍼플렉서티(log perplexity)
• 오른쪽: PG-19에서의 로그 퍼플렉서티
  → 모델이 커질수록 Lion의 속도 향상 효과가 더 커지는 경향을 보임
  → Wiki-40B의 가장 큰 모델은 심각한 overfitting이 관찰되어 생략됨

4.4 언어 모델링 및 파인튜닝

(Language Modeling and Fine-tuning)

이 절에서는 언어 모델링과 파인튜닝(fine-tuning)에 중점을 둔다. 언어 전용 과제에서 우리는 β₁과 β₂를 조정(tuning)하면 AdamW와 Lion 모두에서 성능이 향상된다는 것을 발견했다.
→ 튜닝 관련 내용은 5절을 참고하라.

 

📚 오토리그레시브 언어 모델링 (Autoregressive Language Modeling)

우리는 Wiki-40B(Guo et al., 2020)와 PG-19(Rae et al., 2020)라는 소규모 학술 데이터셋에서 Hua et al. (2022)의 방식에 따라 실험을 수행하였다. 사용한 Transformer 모델은 세 가지 크기로 구성된다:

• Small: 110M 파라미터
• Medium: 336M
• Large: 731M

아키텍처 세부사항은 부록 E 참고.

• 각 모델은 batch당 2¹⁸ 토큰, 총 125K 스텝 동안 학습되었고
• Learning rate 스케줄은 10K warmup 이후 선형 감소
• Context 길이는 Wiki-40B는 512, PG-19는 1,024

그림 7은

• Wiki-40B의 토큰 단위 perplexity,
• PG-19의 단어 단위 perplexity를 나타낸다.

결과적으로, Lion은 AdamW보다 일관되게 더 낮은 validation perplexity를 달성했다.

• Medium 모델 기준 학습 속도:
  • Wiki-40B: 1.6배
  • PG-19: 1.5배
• Large 모델 기준 PG-19에서는 2배의 속도 향상을 기록

🧠 표 5: One-shot 평가 결과

• 세 개의 자연어 생성(NLG) 및 21개의 자연어 이해(NLU) 과제 평균
• GPT-3(Brown et al., 2020), PaLM(Chowdhery et al., 2022)의 결과도 참고용으로 포함
• Lion으로 학습된 LLM은 더 뛰어난 in-context 학습 능력을 보였다
• 전체 과제의 상세 결과는 부록의 표 11 참고

 

📈 대규모 언어 모델 학습

언어 모델과 학습 데이터셋의 규모 확대는 NLP의 혁신을 주도해왔다. 이에 따라 우리는 더 대규모 실험을 수행하였다.

• 학습 데이터셋: GLaM(Du et al., 2022)과 유사하며,
  → 다양한 자연어 사용 사례를 포함한 총 1.6조 토큰으로 구성
• GPT-3 방식을 따라,
  → 1.1B ~ 7.5B 파라미터 규모의 모델 세 개를
  → 300B 토큰, batch size 3M 토큰, context length 1K로 학습

이 모델들은 3개의 NLG 과제와 21개의 NLU 과제에서 평가되었으며 (과제 세부사항은 부록 C 참고), 학습 중 perplexity 차이는 없었지만,
→ Lion은 평균 in-context 학습 능력에서 Adafactor보다 우수했다 (표 5 참고)

• Lion으로 학습한 7.5B 모델은
  • 300B 토큰으로 학습되어,
  • 780B 토큰으로 학습된 PaLM 8B보다도 성능이 우수했음
• Lion의 정확도 향상 (Exact Match 기준):
  • 1.1B 모델: +1.0
  • 2.1B 모델: +0.9
  • 7.5B 모델: +0.6

→ NLG와 NLU 과제 모두에서 Adafactor를 상회

 

🧩 마스크드 언어 모델링 (Masked Language Modeling)

우리는 C4 데이터셋(Raffel et al., 2020)에서 BERT 훈련도 수행하였다. 이 과제는 입력 시퀀스에서 임의로 마스킹된 토큰을 복원하는 것을 요구한다.

• 실험 설정 및 아키텍처는 소규모 오토리그레시브 실험과 동일하게 유지
• Validation perplexity 비교 결과:
  • Small: Lion 4.18 vs. AdamW 4.25
  • Medium: 3.42 vs. 3.54
  • Large: 3.18 vs. 3.25

→ Lion이 모든 크기에서 더 나은 perplexity 달성

→ 학습 곡선은 부록의 그림 11(왼쪽) 참조

 

🔧 표 6: GLUE Dev Set에서의 T5 파인튜닝 성능

• 모델 크기: T5 Base (220M), Large (770M), 11B
• 모든 모델은 batch size 128, 고정 learning rate, 500K 스텝 동안 파인튜닝
• 평가 기준:
  • MRPC, QQP: F1 / Accuracy
  • STS-B: Pearson / Spearman 상관계수
  • 그 외: 각 데이터셋의 기본 metric

결과:

• Lion은 세 모델 크기 모두에서 AdamW보다 우수한 평균 성능을 보였으며,
• 12개의 평가 항목 중 Lion은 각각
  • Base: 10개 승
  • Large: 12개 승
  • 11B: 10개 승

 

🔧 파인튜닝 (Fine-tuning)

우리는 T5 Base (220M), Large (770M), 그리고 가장 큰 11B 모델(Raffel et al., 2020)을 GLUE 벤치마크(Wang et al., 2019a)에서 파인튜닝하였다.

• 모든 모델은 batch size 128, 고정된 학습률로 총 50만 스텝 동안 학습되었다.
• 표 6은 GLUE 개발 세트(dev set)에서의 결과를 보여준다.

평가지표는 다음과 같다:

• MRPC, QQP: F1 점수 / 정확도
• STS-B: Pearson / Spearman 상관계수
• 기타 데이터셋: 각 과제의 기본 평가 지표 사용

평균적으로 볼 때, Lion은 모든 모델 크기에서 AdamW보다 더 나은 성능을 보였다.

• 각각의 12개 평가 항목 중에서 Lion이 이긴 횟수는:
  • T5 Base: 10개
  • T5 Large: 12개
  • T5 11B: 10개

4.5 다른 인기 있는 옵티마이저들과의 비교

(Comparison with Other Popular Optimizers)

우리는 다음의 수작업으로 설계된 대표적인 옵티마이저 4종과:

• RAdam (Liu et al., 2020)
• NAdam (Dozat, 2016)
• AdaBelief (Zhuang et al., 2020)
• AMSGrad (Reddi et al., 2018)

그리고 AutoML을 통해 발견된 옵티마이저 2종:

• PowerSign (Bello et al., 2017)
• AddSign (Bello et al., 2017)

을 사용하여 ViT-S/16 및 ViT-B/16을 ImageNet에서 학습하였다 (데이터 증강은 RandAug 및 Mixup 사용).

 

모든 옵티마이저에 대해 다음 두 가지를 철저히 튜닝하였다:

• 최대 학습률 lr
• Decoupled weight decay 계수 λ
  → (Loshchilov and Hutter, 2019)

그 외 하이퍼파라미터는 모두 Optax 라이브러리의 기본값을 사용하였다.
🔗 https://github.com/deepmind/optax

GitHub - google-deepmind/optax: Optax is a gradient processing and optimization library for JAX.

 

표 7에서 볼 수 있듯, Lion은 여전히 가장 뛰어난 성능을 보여주었다. 베이스라인들 사이에서는 명확한 우위가 없었으며, 다음과 같은 특징이 관찰되었다:

• AMSGrad는 ViT-S/16에서는 가장 좋은 성능,
  → 반대로 ViT-B/16에서는 가장 낮은 성능
• PowerSign과 AddSign은 다른 옵티마이저에 비해 일관되게 낮은 성능을 보였으며,
  → 이는 기존 연구들과 마찬가지로, 자동 탐색된 옵티마이저들이 실제 학습 과제에서 일반화에 어려움을 겪는 경향을 다시 확인한 결과이다.

부록의 그림 10에서는
→ 다섯 개의 적응형 옵티마이저는 매우 유사한 학습 곡선을 보이는 반면,
→ Lion은 독특한 곡선 형태를 보이며 훨씬 빠르게 학습하는 것을 확인할 수 있다.

 

🧪 표 7: 다양한 옵티마이저의 ImageNet 학습 성능

• 모델: ViT-S/16, ViT-B/16
• 데이터 증강: RandAug + Mixup
• Lion이 여전히 가장 우수한 성능,
• 나머지 옵티마이저들은 일관된 우위 없이 혼재된 성능을 보임

4.6 절제 실험 (Ablations)

🔁 모멘텀 추적(Momentum Tracking)

β₁과 β₂의 영향을 분석하기 위해, 우리는 다음과 같은 단순화된 업데이트 규칙과 비교 실험을 수행했다:

m = interp(g, m, β)  
update = sign(m)

이때 두 가지 옵티마이저를 구성하였다:

• Ablation0.9: β = 0.9
• Ablation0.99: β = 0.99

표 7에 나타난 바와 같이,
→ 이 두 절제된(ablated) 옵티마이저는 비교 대상인 5개의 옵티마이저보다도 성능이 낮았으며,
→ 당연히 Lion보다 훨씬 못한 성능을 보였다.

또한, 언어 모델링 과제에 대한 추가 절제 실험(부록의 그림 12 참조)에서도 유사한 결론이 도출되었다.

👉 이러한 결과는 다음을 입증한다:

• 두 개의 선형 보간 함수(interp)를 사용하는 것이 효과적이며,
• 이를 통해 Lion은 gradient의 긴 이력을 기억하면서도,
• 동시에 현재 gradient에 높은 가중치를 부여할 수 있게 된다.

📦 배치 크기의 영향 (Effect of Batch Size)

일부는 sign 연산이 노이즈를 추가하기 때문에, Lion이 방향성을 정확히 결정하려면 큰 배치 크기를 필요로 하는 것 아니냐는 의문을 가질 수 있다. 이러한 의문을 검증하기 위해, 우리는 ViT-B/16 모델을 ImageNet에서 다양한 배치 크기로 학습시켰다.

• 전체 학습 epoch 수는 300으로 고정
• 데이터 증강: RandAug + Mixup 적용

그림 8 (왼쪽)에 따르면:

• AdamW의 최적 배치 크기는 256,
• 반면 Lion의 최적 배치 크기는 4,096

이는 Lion이 더 큰 배치를 선호한다는 것을 보여주지만,
→ 64와 같은 작은 배치 크기에서도 여전히 견고한 성능을 유지함도 확인되었다.

또한, 배치 크기를 32K로 확장하면
→ 총 학습 스텝은 11K로 감소하지만,
→ Lion은 AdamW보다 2.5% 더 높은 정확도(77.9% vs. 75.4%)를 기록하며
→ 대규모 배치 학습 환경에서의 우수한 효과를 보여주었다.

 

📊 그림 8 설명

• 왼쪽: 배치 크기 변화에 따른 절제 실험
  → Lion은 AdamW보다 큰 배치에서 더 높은 성능
• 가운데 / 오른쪽:
  → AdamW와 Lion 각각에 대해 학습률(lr)과 weight decay(λ) 조합을 바꿔가며
  → ViT-B/16을 ImageNet에서 scratch 학습한 성능
  → Lion은 다양한 하이퍼파라미터 설정에 대해 더 강건함

5. 하이퍼파라미터 튜닝 (Hyperparameter Tuning)

공정한 비교를 위해, 우리는 AdamW (또는 Adafactor)와 Lion 모두에 대해 최대 학습률 lr과 decoupled weight decay λ를 로그 스케일로 튜닝하였다.

• AdamW의 기본 설정:
  • β1=0.9, β2=0.999,
  • ϵ=1e^{-8}
• Lion의 기본 설정:
  • 프로그램 탐색 과정에서 발견된 값 사용 → β1=0.9, β2=0.99

단, 4.4절에서 수행한 언어 모델링 실험에서는 다음과 같이 조정하였다:

• AdamW: β1=0.9, β2=0.99
• Lion: β1=0.95, β2=0.98

실험을 통해 우리는 다음을 발견하였다:

• β2​ 값을 낮추면,
  → 과거 gradient 이력의 유지 기간은 짧아지지만,
  → 학습 안정성은 향상된다.

또한, AdamW의 ϵ은 기본값 1e^{-8} 대신
→ 1e^{-6}을 사용하는 것이 실험상 더 안정적이었으며,
→ 이는 RoBERTa(Liu et al., 2019b)에서의 관찰 결과와 유사하다.

 

🔁 Lion에 적절한 학습률과 weight decay 설정

• Lion의 업데이트는 sign 연산에 따라 ±1의 이진 벡터이기 때문에,
  → 다른 옵티마이저보다 노름(norm)이 크다.

→ 따라서 Lion의 적절한 학습률은 AdamW 대비 일반적으로 3~10배 작아야 한다.

• 주의할 점:
  → 초기값, 최대값, 최종값 모두를 동일한 비율로 함께 조정해야 한다.
  → 학습률 스케줄, gradient clipping, update clipping 등 기타 학습 설정은 동일하게 유지
• 실제 적용되는 weight decay는 lr×λ로 계산됨:

update += w * λ  
update *= lr

→ 따라서 Lion에서는 동일한 정규화 효과를 위해 AdamW보다 λ를 3~10배 더 크게 설정해야 한다.

 

🎯 튜닝 난이도 및 하이퍼파라미터 민감도

실제 환경에서 옵티마이저를 채택할 때는, 최대 성능뿐만 아니라,
→ 튜닝의 난이도 및 하이퍼파라미터에 대한 민감도도 중요하다.

그림 8 (가운데 및 오른쪽)에서는
→ ImageNet에서 ViT-B/16을 scratch부터 학습하면서
→ 학습률 lr과 weight decay λ를 함께 변경하여 평가하였다.

히트맵 결과에 따르면,
→ Lion은 AdamW보다 다양한 하이퍼파라미터 설정에 대해 더 강건(robust)함을 보여준다.

 

6. 한계점 (Limitations)

🔍 탐색(Search)의 한계

탐색 공간의 제약을 줄이기 위한 노력을 기울였지만, 여전히 인기 있는 1차 최적화 알고리즘들에 영감을 받은 구조를 따르고 있기 때문에
→ 유사한 알고리즘들에 편향될 수밖에 없다.

또한, 고급 2차 최적화 알고리즘을 구성하는 데 필요한 함수들이 탐색 공간에 포함되어 있지 않다 (Anil et al., 2020; Gupta et al., 2018; Martens and Grosse, 2015 참조).

• 탐색 비용이 여전히 크고,
• 알고리즘 단순화 과정에는 수작업 개입이 필요하다.

미래 연구에서는 다음이 중요할 것이다:

• 탐색 공간의 편향을 더욱 줄여,
  → 보다 새롭고 혁신적인 알고리즘을 발견할 수 있도록 하고,
• 탐색 효율을 개선하는 방향

현재 프로그램 구조는 상당히 단순한 형태인데, 조건문, 반복문, 사용자 정의 함수 등 고급 프로그래밍 구조를 도입했을 때 실용적인 활용 방법을 찾지 못했기 때문이다.
→ 이러한 요소들을 어떻게 통합할 수 있을지 탐색하는 것은 새로운 가능성을 열어줄 수 있는 중요한 방향이다.

 

🦁 Lion의 한계

우리는 Lion을 최대한 다양한 과제에서 평가하려고 했지만,
→ 그 범위는 결국 선택된 실험 과제들로 제한되어 있다.

비전 과제에서는 다음과 같은 특징이 나타난다:

• ResNet 기반 모델에서는
  → Lion, AdamW, momentum SGD 간의 성능 차이가 매우 작다.
  → 이는 CNN이 Transformer보다 최적화가 상대적으로 쉬운 구조이기 때문일 수 있다.
• 강한 데이터 증강(augmentation)을 사용할 경우,
  → Lion의 성능 이점은 줄어든다.

또한 Lion과 AdamW가 유사한 성능을 보이는 과제들도 존재한다:

1. Imagen 텍스트-투-이미지 base 모델
2. 대규모 내부 데이터셋에서 학습된 autoregressive 언어 모델의 perplexity
   • 이는 in-context learning보다 더 신뢰할 수 있는 지표로 여겨질 수 있다
3. C4 데이터셋에서의 마스크드 언어 모델링

이러한 과제들의 공통점은 다음과 같다:

• 데이터셋이 방대하고 품질이 매우 높다
  → 이로 인해 옵티마이저 간의 성능 차이가 상대적으로 줄어든다

또 다른 잠재적 한계는 배치 크기이다.

• 대부분의 경우에서는 병렬화를 위해 배치 크기를 키우는 것이 일반적이지만,
• 배치 크기가 작을 경우 (예: < 64),
  → Lion이 AdamW보다 나은 성능을 보장하지 않는다.

또한, Lion은 여전히 모멘텀을 bfloat16으로 추적해야 하며,
→ 이는 초대형 모델을 훈련할 때 메모리 측면에서 비용이 클 수 있다.

이 문제에 대한 잠재적 해결책은
→ 모멘텀 파라미터를 행렬로 분해(factorize)하여 메모리 사용을 줄이는 것이다.

 

7. 관련 연구 (Related Work)

본 연구는 AutoML 및 메타러닝(meta-learning) 분야에 속하며, 이에는 다음과 같은 하위 영역들이 포함된다:

• Learning to learn
  (Andrychowicz et al., 2016; Ravi and Larochelle, 2017; Wichrowska et al., 2017; Bello et al., 2017; Xiong et al., 2022; Metz et al., 2019, 2022)
• 신경망 아키텍처 탐색(Neural Architecture Search)
  (Real et al., 2019; Zoph and Le, 2017; Pham et al., 2018; Liu et al., 2019a; Chen and Hsieh, 2020; Wang et al., 2021b; So et al., 2019; Chen et al., 2021; Yang et al., 2022; Wang et al., 2021a)
• 하이퍼파라미터 최적화(Hyperparameter Optimization)
  (Li et al., 2017; Jamieson and Talwalkar, 2016; Hutter et al., 2011; Dong et al., 2021)

또한, 진화 알고리즘을 활용해 프로그램을 탐색하는 연구, 즉 유전 프로그래밍(genetic programming)에도 긴 역사가 있다
(Koza, 1994; Brameier et al., 2007; Holland, 1992).

 

우리의 접근 방식은 AutoML-Zero(Real et al., 2020; Peng et al., 2020)와 유사한 기호적(symbolic) 탐색 공간 위에 구축되어 있다. 하지만 기존의 연구들이 고정 차원의 행렬, 벡터, 스칼라를 다루는 장난감 수준의 과제에 초점을 맞췄다면,
→ 우리는 n차원 배열을 다루고 실제 SOTA 과제에 일반화 가능한 프로그램을 목표로 한다.

 

그 외 관련 연구로는 수많은 수작업 옵티마이저들이 있으며 (Kingma and Ba, 2014; Bernstein et al., 2018; Duchi et al., 2011; Shazeer and Stern, 2018; Zhuang et al., 2020; Dozat, 2016; Anil et al., 2020; Liu et al., 2020; Reddi et al., 2018; Gupta et al., 2018; Riedmiller and Braun, 1993; Ma and Yarats, 2019),→ 이들은 3.2절에서 다루었다.

 

8. 결론 (Conclusion)

본 논문은 프로그램 탐색을 통해 최적화 알고리즘을 자동으로 발견하는 방법을 제안하였다. 우리는 다음의 문제들을 해결하기 위한 다양한 기법들을 고안하였다:

• 무한하고 희소한 탐색 공간에서의 탐색 효율성
• 프록시 태스크와 실제 태스크 간의 큰 일반화 격차

이 방법을 통해 우리는 단순하고 효과적인 옵티마이저인 Lion을 발견하였으며, 이 옵티마이저는 메모리 효율성이 높고,다양한 아키텍처, 데이터셋, 과제에 걸쳐 뛰어난 일반화 성능을 보였다.

 

감사의 글 (Acknowledgements)

다음 분들께 감사드립니다 (알파벳 순):
Angel Yu, Boqing Gong, Chen Cheng, Chitwan Saharia, Daiyi Peng, David So, Hanxiao Liu, Hanzhao Lin, Jeff Lund, Jiahui Yu, Jingru Xu, Julian Grady, Junyang Shen, Kevin Regan, Li Sheng, Liu Yang, Martin Wicke, Mingxing Tan, Mohammad Norouzi, Qiqi Yan, Rakesh Shivanna, Rohan Anil, Ruiqi Gao, Steve Li, Vlad Feinberg, Wenbo Zhang, William Chan, Xiao Wang, Xiaohua Zhai, Yaguang Li, Yang Li, Zhuoshu Li, Zihang Dai, Zirui Wang.

그들의 유익한 토론에 감사드리며, Google Brain 팀 전체에게도 풍부한 연구 환경을 제공해주신 것에 깊이 감사드립니다.