On the Importance of Noise Scheduling for Diffusion Models

인공지능

On the Importance of Noise Scheduling for Diffusion Models

JunHan 2024. 11. 27. 17:24

We empirically study the effect of noise scheduling strategies for denoising diffusion generative models. There are three findings: (1) the noise scheduling is crucial for the performance, and the optimal one depends on the task (e.g., image sizes), (2) wh

arxiv.org

초록
우리는 노이즈 스케줄링 전략이 소음 제거 확산 생성 모델에 미치는 영향을 실험적으로 연구한다. 여기에는 세 가지 주요 발견이 있다: (1) 노이즈 스케줄링은 성능에 매우 중요하며, 최적의 스케줄링은 작업에 따라 달라진다 (예: 이미지 크기), (2) 이미지 크기가 커질수록 최적의 노이즈 스케줄링은 더 높은 노이즈 쪽으로 이동한다 (픽셀의 중복성이 증가하기 때문), (3) 입력 데이터를 단순히 상수 b 로 스케일링하는 것은 [1] 노이즈 스케줄링 함수를 고정한 상태에서 (logSNR을 log ⁡ b 만큼 이동시키는 것과 동등) 이미지 크기에 관계없이 좋은 전략이다. 이 간단한 방법은 최근 제안된 순환 인터페이스 네트워크(Recurrent Interface Network, RIN) [10]와 결합했을 때, ImageNet의 고해상도 이미지에 대해 최첨단의 픽셀 기반 확산 모델을 달성할 수 있으며, 단일 스테이지의 종단 간 다양한 고품질 이미지 생성이 가능하다 (해상도 1024 × 1024, 업샘플링이나 캐스케이드 없이).

그림 1: 우리의 단일 스테이지 종단 간 모델(클래스 조건부 ImageNet 이미지로 학습된)로 생성된 랜덤 샘플들로, 고해상도: 512 × 512 (첫 번째 행), 768 × 768 (두 번째 행), 1024 × 1024 (마지막 행)에서의 예시이다. 더 많은 샘플은 그림 6, 7, 8에서 볼 수 있다.

1. 왜 노이즈 스케줄링이 확산 모델에 중요한가?
확산 모델[18, 7, 19, 20, 12, 2]은 데이터를 노이즈화하는 과정을 다음과 같이 정의한다:
𝒙_t = γ(t)𝒙_0 + √(1 − γ(t))ϵ
여기서 𝒙_0는 입력 예시(예: 이미지)이고, ϵ는 등방성 가우시안 분포에서 샘플링한 값이며, t는 0과 1 사이의 연속적인 값이다. 확산 모델의 훈련은 간단하다: 먼저 t ∈ 𝒰(0, 1)에서 t를 샘플링하여 입력 예시 𝒙_0를 𝒙_t로 확산시키고, 소음 제거 네트워크 f(𝒙_t)를 훈련시켜 노이즈 ϵ 또는 깨끗한 데이터 𝒙_0를 예측하도록 한다. t가 균등하게 분포하므로, 노이즈 스케줄 γ(t)는 신경망이 학습하는 노이즈 수준의 분포를 결정한다.

노이즈 스케줄의 중요성은 그림 2의 예시를 통해 증명될 수 있다. 이미지 크기를 증가시키면, 동일한 노이즈 수준(즉, 동일한 γ)에서의 소음 제거 작업이 더 간단해진다. 이는 일반적으로 이미지 크기가 증가함에 따라 데이터 내 정보의 중복성(예: 인접한 픽셀 간의 상관성)이 증가하기 때문이다. 또한, 노이즈가 각각의 픽셀에 독립적으로 추가되기 때문에, 이미지 크기가 증가할수록 원래 신호를 복구하는 것이 더 쉬워진다. 따라서 낮은 해상도에서의 최적 스케줄이 높은 해상도에서도 최적이 아닐 수 있다. 그리고 이에 맞춰 스케줄을 조정하지 않으면 특정 노이즈 수준에 대해 충분히 훈련되지 않을 수 있다. 이러한 유사한 관찰은 동시 연구에서도 확인되었다 [9, 4].

그림 2: 동일한 노이즈 수준(γ = 0.7)에서 노이즈가 추가된 이미지들 (𝒙_t = γ𝒙_0 + √(1 − γ)ϵ). 고해상도 자연 이미지는 일반적으로 (인접한) 픽셀 간 중복도가 더 높아 동일한 수준의 독립적인 노이즈로도 덜 파괴된다는 것을 확인할 수 있다.

2. 노이즈 스케줄링 조정 전략
기존의 노이즈 스케줄링 관련 연구[7, 13, 12, 1, 10]를 바탕으로, 우리는 확산 모델에 대한 두 가지 다른 노이즈 스케줄링 전략을 체계적으로 연구하였다.

2.1 전략 1: 노이즈 스케줄 함수 변경하기
첫 번째 전략은 노이즈 스케줄을 1차원 함수로 매개변수화하는 것이다 [13, 10]. 여기에서는 코사인 또는 시그모이드 함수의 일부를 기반으로 한, 온도 스케일링이 적용된 함수를 소개한다. 원래의 코사인 스케줄은 [13]에서 제안되었으며, 고정된 코사인 곡선 일부로 조정할 수 없는 형태이다. 시그모이드 스케줄은 [10]에서 제안되었다. 이 두 가지 함수 외에도, 우리는 간단한 선형 노이즈 스케줄 함수도 제안한다. 이 함수는 단순히 γ(t) = 1 − t 이다 (이것은 [7]에서 제안된 선형 스케줄과는 다르다). 알고리즘 1에서는 이러한 연속 시간 노이즈 스케줄 함수 γ(t)의 구현 코드를 제시한다.

알고리즘 1: 연속 시간 노이즈 스케줄링 함수 γ(t)

def simple_linear_schedule(t, clip_min=1e-9):
  # 간단히 1-t로 정의된 감마 함수.
  return np.clip(1 - t, clip_min, 1.)

def sigmoid_schedule(t, start=-3, end=3, tau=1.0, clip_min=1e-9):
  # 시그모이드 함수를 기반으로 한 감마 함수.
  v_start = sigmoid(start / tau)
  v_end = sigmoid(end / tau)
  output = sigmoid((t * (end - start) + start) / tau)
  output = (v_end - output) / (v_end - v_start)
  return np.clip(output, clip_min, 1.)

def cosine_schedule(t, start=0, end=1, tau=1, clip_min=1e-9):
  # 코사인 함수를 기반으로 한 감마 함수.
  v_start = math.cos(start * math.pi / 2) ** (2 * tau)
  v_end = math.cos(end * math.pi / 2) ** (2 * tau)
  output = math.cos((t * (end - start) + start) * math.pi / 2) ** (2 * tau)
  output = (v_end - output) / (v_end - v_start)
  return np.clip(output, clip_min, 1.)

그림 3은 하이퍼파라미터 선택에 따른 노이즈 스케줄 함수와 해당 로그 신호 대 잡음 비율(logSNR)을 시각화한 것이다. 코사인과 시그모이드 함수 모두 다양한 노이즈 분포를 매개변수화할 수 있음을 볼 수 있다. 여기서는 노이즈 분포가 더 높은 노이즈 수준에 치우치도록 하이퍼파라미터를 선택했으며, 이러한 설정이 더 유용하다는 것을 발견하였다.

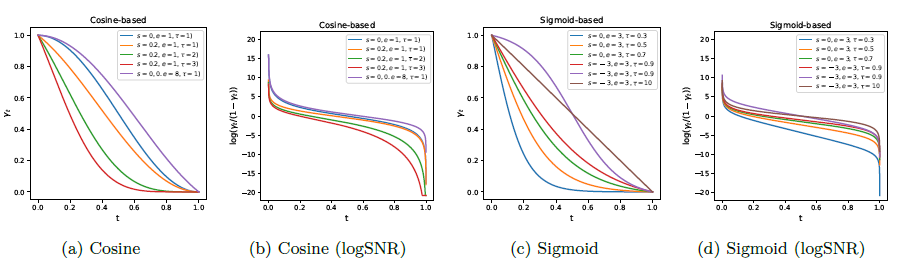
그림 3: 다양한 하이퍼파라미터 선택에 따른 노이즈 스케줄 함수 γ(t)와 해당하는 logSNR. 코사인과 시그모이드 함수의 하이퍼파라미터를 조정하면 다양한 노이즈 스케줄을 얻을 수 있다.

2.2 전략 2: 입력 스케일링 인자 조정
[1]에서 제안된 또 다른 간접적인 노이즈 스케줄링 조정 방법은 입력 𝒙_0를 상수 인자 b로 스케일링하는 것이다. 이로 인해 다음과 같은 노이즈 처리 과정이 발생한다.

𝒙_t = √ γ(t) b 𝒙_0 + √(1 − γ(t)) ϵ

그림 4: 동일한 노이즈 수준(γ = 0.7)에서 노이즈가 추가된 이미지들로, 입력 𝒙_0는 상수 b로 스케일링되었다. 더 작은 스케일링 인자를 사용할수록 동일한 노이즈 수준에서 더 많은 정보가 파괴된다. 노이즈가 추가된 이미지는 분산이 감소함에 따라 더 어두워진다. 스케일링 인자 b를 줄이면 노이즈 수준이 증가하며, 이는 그림 4에서 확인할 수 있다.

b ≠ 1일 때, 입력 𝒙_0가 ϵ와 같은 평균과 분산을 갖더라도 𝒙_t의 분산이 달라질 수 있으며, 이는 성능 감소를 초래할 수 있다 [11]. 이 경우, 분산을 일정하게 유지하기 위해 𝒙_t를 인자 (b^2 - 1)γ(t) + 1의 역수로 스케일링할 수 있다. 그러나 실질적으로는, 𝒙_t를 분산으로 단순히 정규화하여 단위 분산을 갖도록 한 뒤 소음 제거 네트워크 f(⋅)에 입력하는 것이 잘 작동함을 발견하였다. 이러한 분산 정규화 작업은 소음 제거 네트워크의 첫 번째 층으로 볼 수도 있다.

이 입력 스케일링 전략은 위에서 설명한 노이즈 스케줄 함수 γ(t)를 변경하는 것과 유사하지만, 코사인 및 시그모이드 스케줄과 비교했을 때 logSNR에 약간 다른 영향을 미친다. 특히 t가 0에 가까울 때 그 차이가 두드러진다 (그림 5 참조). 실제로 입력 스케일링은 logSNR을 y축을 따라 이동시키면서 그 형태는 변하지 않게 유지한다는 점에서, 위에서 고려한 다른 노이즈 스케줄 함수들과 다르다. 또한, 입력 스케일링을 피하기 위해 γ(t) 함수를 다른 방식으로 매개변수화할 수도 있으며, 이는 동시 연구에서 잘 시연되었다 [9].

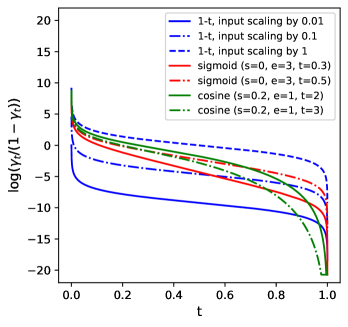
그림 5: 입력 스케일링(간단한 선형 스케줄에서)과 다른 코사인 기반 또는 시그모이드 기반 노이즈 스케줄 함수들 간의 비교. 입력 스케일링은 logSNR을 y축을 따라 이동시키기만 하고 형태를 변경하지 않는 반면, 코사인 및 시그모이드 함수는 t가 1에 가까울 때 더 큰 비중을 두고, t가 작을 때는 영향을 거의 미치지 않는다.

2.3 함께 조합하기: 간단한 복합 노이즈 스케줄링 전략
여기서는 단일 노이즈 스케줄 함수, 예를 들어 γ(t) = 1 − t 를 사용하고 입력을 상수 b로 스케일링하여 두 가지 전략을 결합하는 방법을 제안한다. 훈련 및 추론 전략은 다음과 같다.

훈련 전략

알고리즘 2는 이 결합된 노이즈 스케줄링 전략을 확산 모델 훈련에 통합하는 방법을 보여준다. 주요 변경사항은 파란색으로 강조되어 있다.

알고리즘 2: 결합된 노이즈 스케줄링 전략을 사용하는 확산 모델 훈련

def train_loss(x, gamma=lambda t: 1-t, scale=1, normalize=True):
  """훈련 예시 x에 대한 확산 손실을 반환한다."""
  bsz, h, w, c = x.shape
  # 데이터에 노이즈 추가.
  t = np.random.uniform(0, 1, size=[bsz, 1, 1, 1])
  eps = np.random.normal(0, 1, size=[bsz, h, w, c])
  x_t = np.sqrt(gamma(t)) * scale * x + np.sqrt(1 - gamma(t)) * eps
  # 노이즈 제거 및 손실 계산.
  x_t = x_t / x_t.std(axis=(1, 2, 3), keepdims=True) if normalize else x_t
  eps_pred = neural_net(x_t, t)
  loss = (eps_pred - eps) ** 2
  return loss.mean()

추론/샘플링 전략

훈련 중 분산 정규화를 사용했다면 샘플링 중에도 동일하게 사용해야 한다(즉, 정규화 작업은 소음 제거 네트워크의 첫 번째 층으로 볼 수 있다). 우리는 연속적인 시간 단계 t ∈ [0, 1] 을 사용하므로, 추론 스케줄은 훈련 스케줄과 동일할 필요는 없다. 추론 중에는 0과 1 사이의 시간을 주어진 단계 수로 균일하게 이산화(discretization)하고, 그 후 추론 시점의 노이즈 수준을 결정하기 위해 원하는 γ(t) 함수를 선택할 수 있다. 실제로는 표준 코사인 스케줄이 샘플링에 잘 작동하는 것으로 나타났다.

알고리즘 3: 확산 샘플링 알고리즘

def generate(steps, gamma=lambda t: 1-t, scale=1, normalize=True):
  x_t = normal(mean=0, std=1)
  for step in range(steps):
    # 현재와 다음 상태의 시간을 얻는다.
    t_now = 1 - step / steps
    t_next = max(1 - (step + 1) / steps, 0)
    # eps 예측 및 t_next에서 x로 이동.
    x_t = x_t / x_t.std(axis=(1, 2, 3), keepdims=True) if normalize else x_t
    eps_pred = neural_net(x_t, t_now)
    x_t = ddim_or_ddpm_step(x_t, eps_pred, t_now, t_next)
  return x_t

3.1 설정

우리는 주로 클래스 조건부 ImageNet [15] 이미지 생성을 대상으로 실험을 수행하며, 일반적인 평가 방법을 따릅니다. 평가 지표로 FID [5]와 Inception Score [16]를 사용하였으며, 이는 DDPM의 1000 스텝을 통해 생성된 50K 샘플에 대해 계산됩니다.

모델 사양은 [10]을 따르되, 계산 비용을 절약하기 위해 더 작은 모델과 짧은 전체 훈련 스텝을 사용했습니다 (256 이상의 해상도를 제외하고). 그 결과 일반적으로 성능이 저하되었지만, 노이즈 스케줄링의 개선 덕분에 낮은 해상도(64×64 및 128×128)에서는 비슷한 성능을, 높은 해상도(256×256 이상)에서는 훨씬 더 나은 결과를 달성할 수 있었습니다.

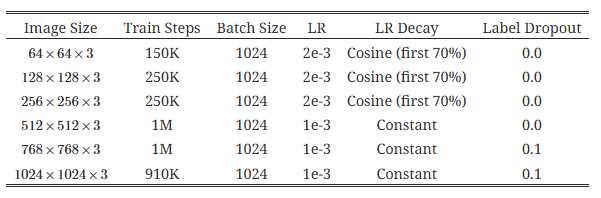
하이퍼파라미터로는, LAMB [21] 옵티마이저를 사용하고, β_1 = 0.9, β_2 = 0.999 이며, 가중치 감소(weight decay)는 0.01, 셀프 컨디셔닝 비율은 0.9, EMA 감쇠율은 0.9999를 사용했습니다. 주요 하이퍼파라미터는 표 1과 2에 요약되어 있습니다.

표 1: 모델 하이퍼파라미터

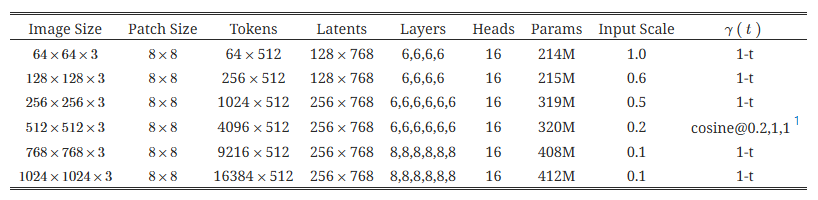
표 2: 훈련 하이퍼파라미터

3.2 전략 1의 효과 (노이즈 스케줄 함수)

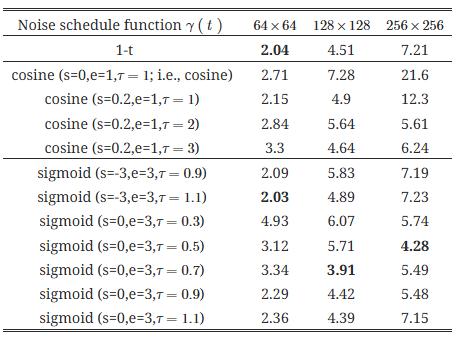
먼저 입력 스케일링을 1로 고정하고, 코사인, 시그모이드, 선형 함수 기반의 노이즈 스케줄의 효과를 평가했습니다. 표 3에서 볼 수 있듯이, 각기 다른 이미지 해상도는 최적의 성능을 얻기 위해 서로 다른 노이즈 스케줄 함수를 필요로 하며, 여러 하이퍼파라미터가 관여하기 때문에 최적의 스케줄을 찾기가 어렵습니다.

표 3: 입력 스케일링을 1로 고정한 상태에서 서로 다른 노이즈 스케줄 함수에 대한 FID (그림 3에서 시각화된 함수 참조). FID는 낮을수록 좋습니다. 해상도에 따라 최적의 스케줄 함수가 상당히 다르며, 찾거나 조정하는 것이 어렵습니다.

3.3 전략 2의 효과 (입력 스케일링)

표 4: 입력 스케일링 인자가 서로 다른 경우의 FID (노이즈 스케줄 함수는 코사인(s=0.2, e=1, τ=1) 또는 1-t로 고정). FID는 낮을수록 좋습니다.

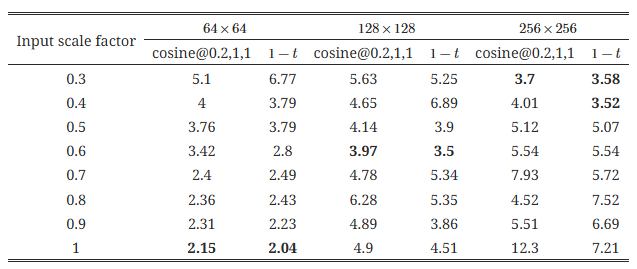
여기서는 노이즈 스케줄 함수를 고정한 상태에서 입력 스케일링 인자를 조정하였습니다. 결과는 표 4에 나와 있습니다. 우리는 다음과 같은 결론을 얻을 수 있었습니다:

이미지 해상도가 증가함에 따라 최적의 입력 스케일링 인자는 작아집니다.
입력 스케일링을 고정한 채로 노이즈 스케줄 함수만 변경한 경우의 최적 결과(표 3)와 비교할 때, 입력 스케일링을 조정하는 것이 더 나은 성능을 보이며 (256×256의 경우 FID가 4.28에서 3.52로 감소), 단일 스케일링 인자만 조정하면 되기 때문에 최적의 값 찾기가 더 쉽습니다. 마지막으로, 1-t 가 코사인(s=0.2, e=1, τ=1)보다 약간 더 나은 노이즈 스케줄로 보입니다.

3.4 간단한 복합 전략과 RIN [10]을 결합하여 최첨단 단일 단계 고해상도 이미지 생성 구현

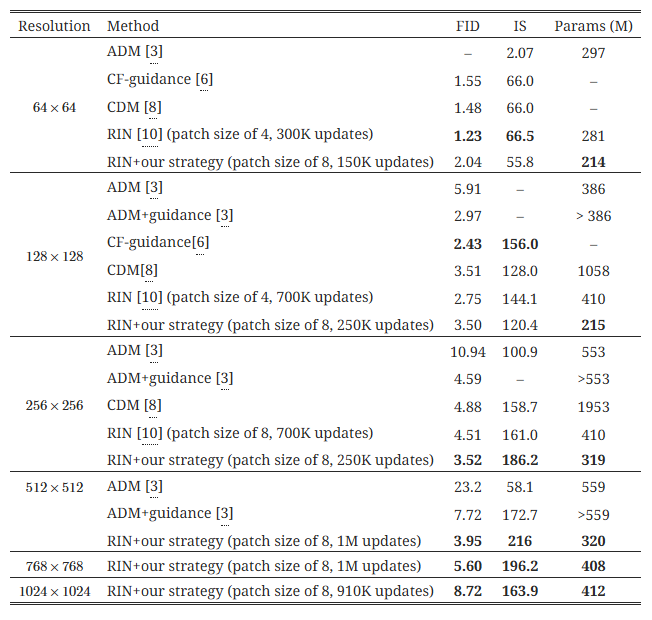
표 5는 간단한 복합 노이즈 스케줄링 전략과 RIN [10]을 결합함으로써, 순수 픽셀 기반의 최첨단 고해상도 이미지 생성이 가능해졌음을 보여줍니다. 우리는 "픽셀"을 학습된 잠재 코드로 대체하는 잠재 확산 모델(latent diffusion model) [14]을 사용하지 않았으며, 이는 우리의 스케줄링 기술이 픽셀 기반 확산 모델에서만 테스트되었기 때문입니다. 하지만 이러한 기법들은 서로 독립적이기 때문에 결합할 가능성도 있습니다. 최첨단 GAN [17]은 비슷하거나 더 나은 성능을 여러 단계의 생성 및 분류기-가이던스(classifier-guidance) [3]를 사용해 달성할 수 있지만, 우리는 이를 정량적 평가에 사용하지 않았습니다.

표 5: ImageNet에서 최첨단 클래스 조건부 픽셀 기반 이미지 생성 모델 비교. FID는 낮을수록, IS는 높을수록 좋습니다. 우리의 결과(RIN 기반)는 캐스케이드/업샘플링이나 가이던스를 사용하지 않습니다.

3.5 생성된 샘플 시각화

해상도 512×512 이미지에 대해서는 레이블 드롭아웃을 사용하지 않았지만, 샘플링 중 클래스-프리 가이던스(classifier-free guidance) [6]가 생성된 샘플의 충실도를 향상시킴을 발견했습니다. 따라서 모든 시각화 샘플은 가이던스 가중치 3으로 생성했습니다. 그림 6, 7, 8은 우리가 훈련한 모델에서 생성된 이미지 샘플을 보여줍니다. 주어진 클래스에 조건부로 생성된 무작위 샘플들이며, 따로 선택되지 않은 샘플들입니다. 전체적으로 보면, 다양한 해상도에서 전반적인 구조가 잘 유지되지만, 작은 스케일에서 객체의 세부적인 부분은 다소 불완전할 수 있습니다. 모델 또는 데이터셋의 크기를 확장하거나(예: 단순 클래스 레이블 대신 더 세부적인 텍스트 설명 사용), 하이퍼파라미터 조정을 통해 이러한 부분을 개선할 수 있을 것으로 생각됩니다(고해상도에 대해서는 충분히 조정하지 않았습니다).

4. 결론

본 연구에서는 확산 모델을 위한 노이즈 스케줄링 전략을 실험적으로 연구하고, 그 중요성을 보여주었습니다. 노이즈 스케줄링은 이미지 생성뿐만 아니라 범용적 분할 [1] 같은 다른 작업에서도 중요한 역할을 합니다. 입력 스케일링 인자를 조정하는 간단한 전략 [1]이 다양한 이미지 해상도에서 잘 작동합니다. 최근 제안된 RIN 아키텍처 [10]와 결합하면, 우리의 노이즈 스케줄링 전략은 고해상도 이미지의 단일 단계 생성을 가능하게 합니다. 실무자들에게는, 새로운 작업이나 데이터셋을 위한 확산 모델을 훈련할 때 적절한 노이즈 스케줄링 방식을 선택하는 것이 중요하다는 점을 시사합니다.

그림 6: 우리의 단일 단계 종단 간 모델에 의해 생성된 512×512 해상도의 무작위 샘플들 (클래스 조건부 ImageNet 이미지로 훈련된 모델). 클래스들은 딸기(949), 오렌지(950), 마코앵무(88), 호랑이(292), 판다(388), 나무 개구리(31), 카트(573), 금붕어(1), 페키니즈(154), 수달(360), 테디 베어(850), 북극 늑대(270), 산호초(973), 상자 거북(37), 우주 왕복선(812), 장수거북(33), 견인차(864), 트랙터(866), 트레일러 트럭(867), 펨브로크 웰시 코기(263), 에스프레소 메이커(550), 스쿨 버스(779), 커피 머그잔(504), 개 썰매(537), 홍학(130).

그림 7: 우리의 단일 단계 종단 간 모델에 의해 생성된 768×768 해상도의 무작위 샘플들 (클래스 조건부 ImageNet 이미지로 훈련된 모델). 클래스들은 딸기(949), 오렌지(950), 마코앵무(88), 호랑이(292), 판다(388), 치즈버거(933), 허스키(250), 유황앵무(89), 화산(980), 사자(291), 골든 리트리버(207), 호숫가(975), 레드 판다(387), 아이스크림(928), 로리킷(90), 북극 여우(279), 고속 열차(466), 던지네스 크랩(118), 풍선(417), 절벽(972).

그림 8: 우리의 단일 단계 종단 간 모델에 의해 생성된 1024×1024 해상도의 무작위 샘플들 (클래스 조건부 ImageNet 이미지로 훈련된 모델). 클래스들은 딸기(949), 오렌지(950), 마코앵무(88), 호랑이(292), 판다(388), 치즈버거(933), 나무 개구리(31), 우주 왕복선(812), 장수거북(33), 견인차(864), 트랙터(866), 트레일러 트럭(867), 사자(291), 골든 리트리버(207), 에스프레소 메이커(550), 스쿨 버스(779), 아이스크림(928), 로리킷(90), 고속 열차(466), 풍선(417).

감사의 말: 우리는 David Fleet과 Allan Jabri에게 유익한 논의에 대해 감사드립니다.

2301.10972v4.pdf

3.84MB