https://arxiv.org/abs/1312.6114
Auto-Encoding Variational Bayes
How can we perform efficient inference and learning in directed probabilistic models, in the presence of continuous latent variables with intractable posterior distributions, and large datasets? We introduce a stochastic variational inference and learning
arxiv.org
초록
연속적인 잠재 변수와 처리하기 어려운 사후 분포를 가진 방향성 확률 모델에서, 대규모 데이터셋을 처리하면서 효율적인 추론과 학습을 어떻게 수행할 수 있을까요? 우리는 대규모 데이터셋에 적용할 수 있고, 일부 온건한 미분 가능성 조건 하에서 처리하기 어려운 경우에서도 동작하는 확률적 변분 추론 및 학습 알고리즘을 소개합니다. 우리의 기여는 두 가지로 나뉩니다. 첫째, 변분 하한을 재매개화(reparameterization)하면 표준 확률적 경사 하강법을 사용하여 간단히 최적화할 수 있는 하한 추정치를 얻을 수 있음을 보입니다. 둘째, 독립적이고 동일한 분포(i.i.d.)를 가진 데이터셋에서 데이터 포인트별로 연속적인 잠재 변수를 가진 경우, 제안된 하한 추정치를 사용하여 다루기 어려운 사후 분포에 근사 추론 모델(인식 모델이라고도 함)을 맞춤으로써 사후 추론의 효율성을 특히 높일 수 있음을 보입니다. 이론적 장점은 실험 결과에서도 반영됩니다.
1. 서론
연속적인 잠재 변수 및/또는 파라미터가 처리하기 어려운 사후 분포를 가진 방향성 확률 모델에서, 효율적인 근사 추론과 학습을 어떻게 수행할 수 있을까요? 변분 베이지안(VB) 접근법은 처리하기 어려운 사후 분포에 대한 근사를 최적화하는 것을 포함합니다. 그러나 일반적인 경우, 흔히 사용되는 평균장(mean-field) 접근법은 근사된 사후 분포에 대한 기대값의 해석적 해결을 요구하며, 이는 역시 처리하기 어렵습니다. 우리는 변분 하한을 재매개화(reparameterization)하여 하한의 단순한 미분 가능하고 편향되지 않은 추정치를 제공할 수 있음을 보입니다. 이 SGVB(Stochastic Gradient Variational Bayes) 추정치는 연속적인 잠재 변수 및/또는 파라미터를 가진 거의 모든 모델에서 효율적인 근사 사후 추론에 사용할 수 있으며, 표준 확률적 경사 상승 기법을 사용해 간단히 최적화할 수 있습니다. 독립적이고 동일한 분포(i.i.d.)의 데이터셋과 데이터 포인트별로 연속적인 잠재 변수를 가진 경우에 대해, 우리는 Auto-Encoding VB(AEVB) 알고리즘을 제안합니다. AEVB 알고리즘에서는 SGVB 추정치를 사용해 인식 모델을 최적화함으로써 추론과 학습을 특히 효율적으로 수행할 수 있습니다. 이를 통해 단순한 조상 샘플링(ancestral sampling)을 사용하여 매우 효율적인 근사 사후 추론을 수행할 수 있게 되며, 이에 따라 비싼 반복적 추론 방식(예: MCMC)이 필요 없이 모델 파라미터를 효율적으로 학습할 수 있습니다. 학습된 근사 사후 추론 모델은 인식, 노이즈 제거, 표현 및 시각화 등의 다양한 작업에도 사용할 수 있습니다. 인식 모델에 신경망을 사용할 경우, 우리는 변분 오토인코더(variational auto-encoder)에 도달하게 됩니다.
2. 방법
이 섹션에서 제시하는 전략은 연속적인 잠재 변수를 가진 다양한 방향성 그래프 모델에 대한 하한 추정치(확률적 목적 함수)를 도출하는 데 사용할 수 있습니다. 우리는 여기서 독립적이고 동일한 분포(i.i.d.)의 데이터셋에서 데이터 포인트별로 잠재 변수를 가지며, (글로벌) 파라미터에 대해 최대 가능도(ML) 또는 최대 사후 확률(MAP) 추론을 수행하고, 잠재 변수에 대해 변분 추론을 수행하려는 일반적인 경우에 한정하겠습니다. 예를 들어, 이 시나리오를 글로벌 파라미터에 대해서도 변분 추론을 수행하는 경우로 확장하는 것은 간단하며, 해당 알고리즘은 부록에 포함되어 있지만, 그 경우에 대한 실험은 향후 연구로 남겨둡니다. 우리의 방법은 온라인, 비정상(non-stationary) 환경, 예를 들어 스트리밍 데이터에도 적용할 수 있지만, 여기서는 단순화를 위해 고정된 데이터셋을 가정합니다.


-----------------------------------------------------------------------------------------------------------------------------------------------------------------
- 관찰 데이터 (왼쪽 빨간 점들): 이것은 우리가 직접 볼 수 있는 데이터입니다. 예를 들어, 설문조사 응답이나 측정된 값들이 될 수 있습니다.
- 잠재 변수 (중앙 상단 파란 원): 이는 직접 관찰할 수 없지만 데이터에 영향을 미치는 숨겨진 요인입니다. 우리의 분석 방법은 이를 추정하려고 합니다.
- 분석 모델 (중앙 녹색 사각형): 이것은 우리가 사용하는 통계적 방법이나 알고리즘입니다. 관찰 데이터와 잠재 변수를 입력으로 받아 처리합니다.
- 분석 결과 (오른쪽 주황색 삼각형): 이는 모델이 생성한 출력입니다. 여기에는 전체적인 패턴, 예측, 또는 인사이트가 포함될 수 있습니다.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------
2.1 문제 시나리오

매우 중요한 점은, 우리는 일반적으로 자주 사용하는 주변 또는 사후 확률에 대한 단순화된 가정을 하지 않는다는 것입니다. 반대로, 우리는 다음과 같은 경우에서도 효율적으로 작동하는 일반적인 알고리즘에 관심이 있습니다:

우리는 위의 시나리오에서 세 가지 관련된 문제에 관심을 가지고 있으며, 이를 해결하기 위한 솔루션을 제안합니다:
- 매개변수 θ에 대한 효율적인 근사 최대 가능도(ML) 또는 최대 사후 확률(MAP) 추정. 매개변수 자체가 분석의 대상이 될 수 있습니다. 예를 들어, 어떤 자연 과정을 분석하고 있을 때 유용할 수 있습니다. 또한 이 매개변수들은 숨겨진 랜덤 프로세스를 모방하고 실제 데이터와 유사한 인공 데이터를 생성할 수 있게 해줍니다.
- 주어진 관측 값 x에 대해 선택된 매개변수 θ로 잠재 변수 z의 효율적인 근사 사후 추론. 이는 코딩 또는 데이터 표현 작업에 유용합니다.
- 변수 x의 효율적인 근사 주변 추론. 이를 통해 x에 대한 사전 확률이 필요한 모든 종류의 추론 작업을 수행할 수 있습니다. 컴퓨터 비전에서 흔한 응용 예로는 이미지 노이즈 제거, 인페인팅(inpainting) 및 초해상도(super-resolution) 등이 있습니다.

-----------------------------------------------------------------------------------------------------------------------------------------------------------------
가우시안 분포를 항상 가정한다.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------
2.2 변분 경계(Variational Bound)

-----------------------------------------------------------------------------------------------------------------------------------------------------------------
몬테카를로 그래디언 추정기는 왜 높은 분산을 가지지? 그리고 이는 왜Auto-Encoding Variational Bayes에 어울리지 않지?
- 몬테카를로 그래디언트 추정기의 높은 분산: a. 샘플링 기반: 몬테카를로 방법은 무작위 샘플링에 기반합니다. 이는 추정값이 실제 값 주변에서 변동할 수 있음을 의미합니다. b. 제한된 샘플 수: 실용적인 이유로 사용하는 샘플의 수가 제한적이어서, 추정의 정확도가 떨어질 수 있습니다. c. 복잡한 분포: 추정하려는 분포가 복잡할수록 정확한 추정이 어려워지고, 이는 분산을 증가시킵니다. d. 차원의 저주: 고차원 공간에서는 샘플링의 효율성이 떨어져 분산이 더 커질 수 있습니다.
- AEVB에 적합하지 않은 이유: a. 학습의 불안정성: 높은 분산은 학습 과정을 불안정하게 만들어 모델의 수렴을 방해할 수 있습니다. b. 계산 비용: 분산을 줄이기 위해 더 많은 샘플이 필요하면, 계산 비용이 크게 증가합니다. c. 그래디언트 소실 문제: 높은 분산으로 인해 일부 중요한 그래디언트 정보가 소실될 수 있습니다. d. 최적화의 어려움: 높은 분산은 최적화 알고리즘이 올바른 방향을 찾는 것을 어렵게 만듭니다. e. 재매개변수화 트릭의 효과성: AEVB에서는 재매개변수화 트릭(reparameterization trick)을 사용하여 이러한 문제를 효과적으로 해결할 수 있습니다. 이 방법은 몬테카를로 추정보다 낮은 분산을 가집니다.




-----------------------------------------------------------------------------------------------------------------------------------------------------------------
2.3 SGVB 추정기와 AEVB 알고리즘





-----------------------------------------------------------------------------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------------------------------------------------------------------------
2.4 재매개화 기법(Reparameterization Trick)



3 예시: 변분 오토인코더(Variational Auto-Encoder)


4 관련 연구
우리의 지식에 따르면, Wake-Sleep 알고리즘 [HDFN95]은 동일한 일반적인 연속 잠재 변수 모델에 적용할 수 있는 유일한 온라인 학습 방법입니다. 우리의 방법과 마찬가지로, Wake-Sleep 알고리즘은 실제 사후 분포를 근사하는 인식 모델을 사용합니다. 그러나 Wake-Sleep 알고리즘의 단점은 두 가지 목적 함수를 동시에 최적화해야 한다는 점이며, 이 두 함수는 함께 주변 우도(marginal likelihood)의 최적화(또는 그 하한)에 해당하지 않는다는 것입니다. Wake-Sleep 알고리즘의 장점은 이산 잠재 변수를 포함한 모델에도 적용할 수 있다는 점입니다. Wake-Sleep 알고리즘은 데이터 포인트당 AEVB와 동일한 계산 복잡도를 가집니다.
최근 확률적 변분 추론(Stochastic Variational Inference) [HBWP13]이 점점 더 많은 관심을 받고 있습니다. 최근 [BJP12]에서는 섹션 2.1에서 논의한 순진한 그래디언트 추정기의 높은 분산을 줄이기 위해 제어 변량 스킴을 도입하였으며, 이를 사후 분포의 지수형 가족 근사에 적용했습니다. [RGB13]에서는 원래의 그래디언트 추정기의 분산을 줄이기 위한 일반적인 방법, 즉 제어 변량 스킴이 소개되었습니다. [SK13]에서는 이 논문에서 사용된 것과 유사한 재매개화를 사용하여 지수형 가족 근사 분포의 자연 파라미터를 학습하는 확률적 변분 추론 알고리즘의 효율적인 버전을 구현했습니다.
AEVB 알고리즘은 방향성 확률 모델(변분 목적을 통해 학습된)과 오토인코더 간의 연결을 드러냅니다. 선형 오토인코더와 특정 종류의 생성 선형-가우시안 모델 간의 연결은 오래전부터 알려져 있었습니다. [Row98]에서는 주성분 분석(PCA)이 사전 p(z)=N(0,I)와 조건부 분포 p(x∣z)=N(x;Wz,ϵI)를 가지는 선형-가우시안 모델의 특수한 경우(특히 ϵ\epsilon이 무한소로 작은 경우)의 최대 가능도(ML) 해와 일치한다는 것을 보였습니다.
오토인코더에 관한 최근 관련 연구 [VLL+10]에서는 규제되지 않은(unregularized) 오토인코더의 학습 기준이 입력 X와 잠재 표현 Z 간의 상호 정보의 하한을 최대화하는 것과 일치한다는 것을 보였습니다(인포맥스 원리 [Lin89] 참조). 상호 정보를 최대화하는 것은 조건부 엔트로피를 최대화하는 것과 동등하며, 이는 오토인코더 모델 하에서 데이터의 기대 로그 가능도, 즉 음의 재구성 오류에 의해 하한이 설정됩니다 [VLL+10]. 그러나 이 재구성 기준만으로는 유용한 표현을 학습하기에 충분하지 않다는 것이 잘 알려져 있습니다 [BCV13]. 오토인코더가 유용한 표현을 학습하도록 하는 규제 기법들이 제안되었으며, 이는 노이즈 제거, 수축, 희소 오토인코더 변형을 포함합니다 [BCV13]. SGVB 목표는 변분 하한(예: 식 (10))에 의해 지시되는 정규화 항을 포함하며, 유용한 표현을 학습하는 데 필요한 일반적인 정규화 하이퍼파라미터를 필요로 하지 않습니다. 이와 관련된 것으로는 예측 희소 분해(PSD) [KRL08]와 같은 인코더-디코더 구조가 있으며, 여기서 우리는 약간의 영감을 얻었습니다. 또한 최근 소개된 생성 확률 네트워크(Generative Stochastic Networks) [BTL13]도 관련이 있는데, 여기서는 노이즈가 있는 오토인코더가 마르코프 체인의 전이 연산자를 학습하여 데이터 분포에서 샘플을 생성합니다. [SL10]에서는 Deep Boltzmann Machines의 효율적인 학습을 위해 인식 모델을 사용했습니다. 이러한 방법들은 비정규화된 모델(즉, 볼츠만 머신과 같은 방향성 없는 모델) 또는 희소 코딩 모델에 초점을 맞추고 있는 반면, 우리는 일반적인 방향성 확률 모델의 학습을 위한 알고리즘을 제안하고 있습니다.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------
- 연구의 주요 내용:
- 규제되지 않은 오토인코더의 학습 기준이 입력 X와 잠재 표현 Z 사이의 상호 정보(mutual information)의 하한을 최대화하는 것과 일치한다는 것을 보였습니다.
- 이는 오토인코더가 단순히 입력을 재구성하는 것이 아니라, 입력의 정보를 최대한 보존하는 잠재 표현을 학습한다는 것을 의미합니다.
- 상호 정보 (Mutual Information):
- 두 변수 간의 상호 의존성을 측정하는 정보이론의 개념입니다.
- I(X;Z) = H(X) - H(X|Z) = H(Z) - H(Z|X) 여기서 H는 엔트로피를 나타냅니다.
- 인포맥스 원리와의 연관성:
- 인포맥스 원리는 신경망이 입력과 출력 사이의 상호 정보를 최대화하는 방향으로 학습한다고 주장합니다.
- 이 연구 결과는 오토인코더가 인포맥스 원리를 따르고 있음을 보여줍니다.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------
최근 제안된 DARN 방법 [GMW13]도 오토인코딩 구조를 사용하여 방향성 확률 모델을 학습하지만, 이 방법은 이진 잠재 변수에 적용됩니다. 더욱 최근에는 [RMW14]에서 우리가 이 논문에서 설명한 재매개화 기법을 사용하여 오토인코더, 방향성 확률 모델 및 확률적 변분 추론 간의 연결을 강조했습니다. 그들의 연구는 우리의 연구와 독립적으로 개발되었으며 AEVB에 대한 추가적인 관점을 제공합니다.
5 실험
우리는 MNIST와 Frey Face 데이터셋의 이미지를 생성하는 모델을 학습하고, 변분 하한 및 추정된 주변 우도를 기준으로 학습 알고리즘을 비교했습니다. 3장에서 사용한 생성 모델(인코더)과 변분 근사(디코더)를 사용했으며, 여기서 설명한 인코더와 디코더는 동일한 수의 은닉 유닛을 가지고 있습니다. Frey Face 데이터가 연속적이기 때문에, 우리는 가우시안 출력을 가진 디코더를 사용했습니다. 이 디코더는 인코더와 동일하지만, 평균은 디코더 출력에서 시그모이드 활성화 함수를 사용하여 (0, 1) 범위로 제한되었습니다. 여기서 은닉 유닛은 인코더와 디코더의 신경망의 은닉층을 의미합니다.
파라미터는 확률적 경사 상승법을 사용하여 업데이트되었으며, 그래디언트는 하한 추정치를 미분하여 계산되었습니다(알고리즘 1 참조). 여기에 사전 p(θ)=N(0,I)에 해당하는 작은 가중치 감소 항이 추가되었습니다. 이 목표의 최적화는 근사 최대 사후 확률(MAP) 추정과 동일하며, 우도 그래디언트는 하한의 그래디언트로 근사되었습니다.
우리는 AEVB의 성능을 Wake-Sleep 알고리즘 [HDFN95]과 비교했습니다. Wake-Sleep 알고리즘과 변분 오토인코더 모두에서 동일한 인코더(인식 모델이라고도 함)를 사용했습니다. 모든 파라미터, 즉 변분 파라미터와 생성 파라미터는 N(0,0.01)에서 무작위로 샘플링하여 초기화되었으며, MAP 기준을 사용해 확률적으로 공동 최적화되었습니다. 학습 초기 몇 번의 반복에서 성능을 기준으로 Adagrad [DHS10]로 스텝 사이즈를 조정했으며, Adagrad 글로벌 스텝 사이즈 파라미터는 0.01, 0.02, 0.1 중에서 선택되었습니다. 데이터 포인트당 샘플 L=1개를 사용한 크기 M=100의 미니배치가 사용되었습니다.
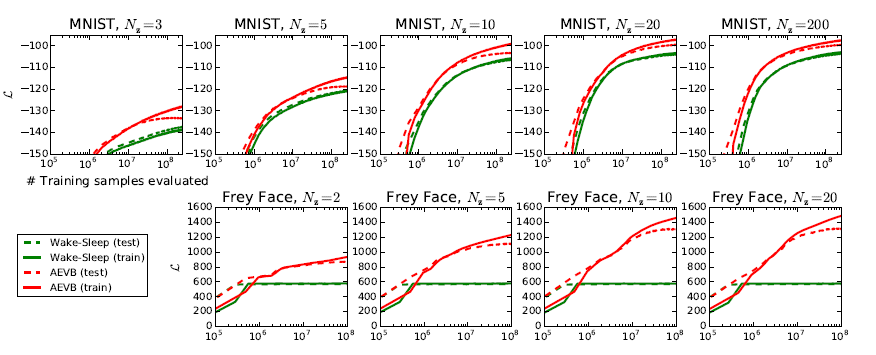
그림 2: 잠재 공간의 차원(Nz)이 다른 경우에 대해, 하한을 최적화하는 측면에서 AEVB 방법과 Wake-Sleep 알고리즘을 비교한 결과입니다. 우리의 방법은 모든 실험에서 훨씬 더 빠르게 수렴했고, 더 나은 해를 도출했습니다. 흥미롭게도, 더 많은 잠재 변수를 사용하는 것이 과적합을 초래하지 않았습니다. 이는 하한의 정규화 효과로 설명됩니다. 수직 축: 데이터 포인트당 추정된 평균 변분 하한. 추정치의 분산은 작아서(< 1) 생략되었습니다. 수평 축: 평가된 학습 포인트 수. 인텔 제온 CPU에서 약 40 GFLOPS의 성능으로 백만 개의 학습 샘플을 처리하는 데 약 20-40분이 소요되었습니다.
우도 하한(Likelihood Lower Bound)
우리는 MNIST 데이터셋의 경우 500개의 은닉 유닛을, Frey Face 데이터셋의 경우 200개의 은닉 유닛을 가진 생성 모델(디코더)과 이에 대응하는 인코더(즉, 인식 모델)를 학습했습니다. Frey Face 데이터셋은 상당히 작은 데이터셋이기 때문에 과적합을 방지하기 위해 은닉 유닛의 수를 줄였습니다. 선택한 은닉 유닛 수는 오토인코더에 관한 이전 문헌을 기반으로 하였으며, 다양한 알고리즘의 상대적 성능은 이러한 선택에 대해 크게 민감하지 않았습니다. 그림 2는 하한을 비교한 결과를 보여줍니다. 흥미롭게도, 불필요한 잠재 변수가 과적합을 초래하지 않았으며, 이는 변분 하한의 정규화 특성으로 설명됩니다.
주변 우도(Marginal Likelihood)
아주 저차원의 잠재 공간에서는 MCMC 추정기를 사용하여 학습된 생성 모델의 주변 우도를 추정할 수 있습니다. 주변 우도 추정기에 대한 추가 정보는 부록에서 확인할 수 있습니다. 인코더와 디코더로는 다시 신경망을 사용했으며, 이번에는 100개의 은닉 유닛과 3개의 잠재 변수를 사용했습니다. 잠재 공간의 차원이 높아지면 추정이 신뢰할 수 없게 됩니다. 이번에도 MNIST 데이터셋을 사용했습니다. AEVB와 Wake-Sleep 방법은 하이브리드 몬테카를로(HMC) [DKPR87] 샘플러와 함께 몬테카를로 EM(MCEM)과 비교되었습니다. 세 가지 알고리즘의 수렴 속도를 소규모 및 대규모 학습 세트 크기에 대해 비교했습니다. 결과는 그림 3에 나와 있습니다.
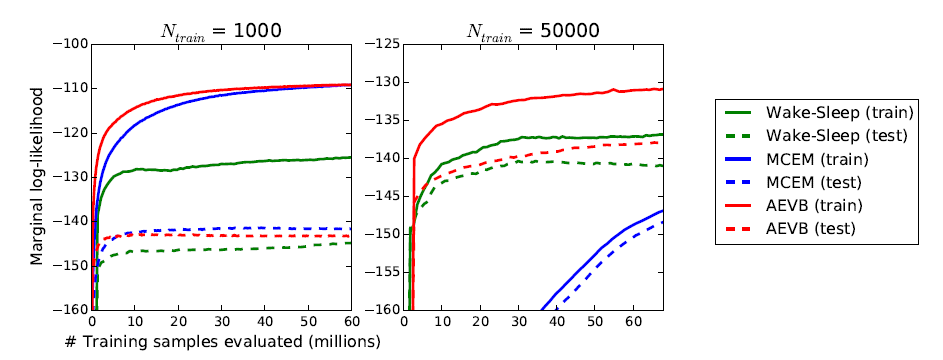
그림 3: AEVB와 Wake-Sleep 알고리즘, 몬테카를로 EM을 서로 다른 학습 포인트 수에 대해 추정된 주변 우도 기준으로 비교한 결과입니다. 몬테카를로 EM은 온라인 알고리즘이 아니며, (AEVB 및 Wake-Sleep 방법과 달리) 전체 MNIST 데이터셋에 효율적으로 적용될 수 없습니다.
고차원 데이터의 시각화
만약 저차원 잠재 공간(예: 2차원)을 선택하면, 학습된 인코더(인식 모델)를 사용하여 고차원 데이터를 저차원 매니폴드로 투영할 수 있습니다. MNIST와 Frey Face 데이터셋에 대한 2차원 잠재 매니폴드의 시각화는 부록 A에서 확인할 수 있습니다.
6 결론
우리는 연속 잠재 변수를 효율적으로 근사 추론하기 위한 새로운 변분 하한 추정기인 확률적 경사 VB(SGVB)를 소개했습니다. 제안된 추정기는 표준 확률적 경사 방법을 사용해 간단히 미분하고 최적화할 수 있습니다. i.i.d. 데이터셋과 데이터 포인트별 연속 잠재 변수를 가진 경우에 대해, 우리는 SGVB 추정기를 사용하여 근사 추론 모델을 학습하는 효율적인 추론 및 학습 알고리즘인 Auto-Encoding VB(AEVB)를 도입했습니다. 이론적 장점은 실험 결과에서 반영되었습니다.
7 미래 작업
SGVB 추정기와 AEVB 알고리즘은 연속 잠재 변수를 사용하는 거의 모든 추론 및 학습 문제에 적용할 수 있으므로, 향후 연구 방향은 매우 많습니다: (i) 인코더와 디코더로 심층 신경망(예: 합성곱 신경망)을 사용하여 계층적 생성 아키텍처 학습, AEVB와 함께 공동 학습; (ii) 시계열 모델(즉, 동적 베이지안 네트워크); (iii) SGVB를 글로벌 파라미터에 적용; (iv) 잠재 변수를 포함한 지도 학습 모델, 복잡한 노이즈 분포 학습에 유용함.
'인공지능' 카테고리의 다른 글
| Going Deeper with Convolutions (InceptionNet, 1x1 convolution, GoogleNet) (2) | 2024.08.12 |
|---|---|
| Beam Search Strategies for Neural Machine Translation (3) | 2024.08.11 |
| Attention Is All You Need (1) | 2024.08.09 |
| Feature Pyramid Networks for Object Detection (2) | 2024.08.08 |
| U-Net: Convolutional Networks for Biomedical Image Segmentation (1) | 2024.08.07 |



