LinkedIn Google Research 페이지: Quantum computers offer many promising applications dependent on greatly… | 댓글 13
Quantum computers offer many promising applications dependent on greatly improved performance. Read how we’ve combined quantum error correction with our latest… | 댓글 13
www.linkedin.com
https://research.google/blog/making-quantum-error-correction-work/
Making quantum error correction work
Willow: beating the threshold Operating “below the threshold” has been a goal for error corrected quantum computing since its inception in the 1990s. However, after almost 30 years of advancement in device fabrication, calibration, and qubit design, qu
research.google
양자 오류 수정의 현실화
2024년 12월 9일
마이클 뉴먼(Michael Newman)과 케빈 사칭어(Kevin Satzinger), 연구 과학자, Google Research, Google Quantum AI 팀
오늘 우리는 Willow를 소개합니다. Willow는 오류 수정된 큐비트가 규모가 커질수록 기하급수적으로 성능이 향상되는 최초의 양자 프로세서입니다.
양자 컴퓨터는 화학, 신약 개발, 최적화, 암호화 등 다양한 분야에서 유망한 응용 가능성을 제공합니다. 이러한 응용 대부분은 수십억, 심지어는 수조 개의 연산을 신뢰성 있게 수행해야 합니다. 이는 현재 웹 브라우저가 처리하는 작업에 비하면 많지 않은 양일지도 모릅니다. 그러나 양자 정보는 매우 섬세하며, 최첨단 양자 장치조차도 천 번의 연산 중 하나 이상에서 실패를 경험할 가능성이 높습니다. 양자 컴퓨터가 잠재력을 발휘하려면 성능이 극적으로 개선되어야 합니다.
오늘 Nature에 게재된 “Quantum error correction below the surface code threshold” 논문에서는 양자 컴퓨터 성능에 있어 질적인 변화를 보고합니다. 이 변화는 양자 오류 수정과 최신 초전도 양자 프로세서인 Willow를 결합하여 이루어졌습니다. Willow는 오류 수정된 큐비트가 규모가 커질수록 기하급수적으로 더 나아지는 첫 번째 프로세서입니다. 우리가 인코딩된 큐비트를 3x3에서 5x5, 7x7 크기의 물리적 큐비트 격자로 확장할 때마다 인코딩된 오류율이 두 배로 줄어드는 결과를 보였습니다. 이는 거의 30년 동안 양자 컴퓨팅의 목표였던 양자 오류 수정이 약속한 기하급수적인 오류 억제를 입증하며, 대규모 양자 응용 프로그램의 가능성을 여는 핵심 요소입니다.
규모가 커질수록 나아지는 오류 수정 큐비트
양자 컴퓨터를 더 신뢰성 있게 만들기 위해 큐비트 그룹을 활용해 오류를 수정할 수 있습니다. 표면 코드(surface code) 양자 컴퓨팅에서는 각 그룹이 큐비트로 이루어진 d×d 정사각 격자를 형성하며, 이를 표면 코드라고 부르고 단일 인코딩 또는 "논리적" 큐비트를 나타냅니다. 표면 코드 격자가 클수록 더 많은 오류를 감지하고 수정할 수 있습니다. 이론적으로는 격자가 커질수록 논리적 큐비트가 더욱 보호되어 논리적 성능이 개선됩니다.
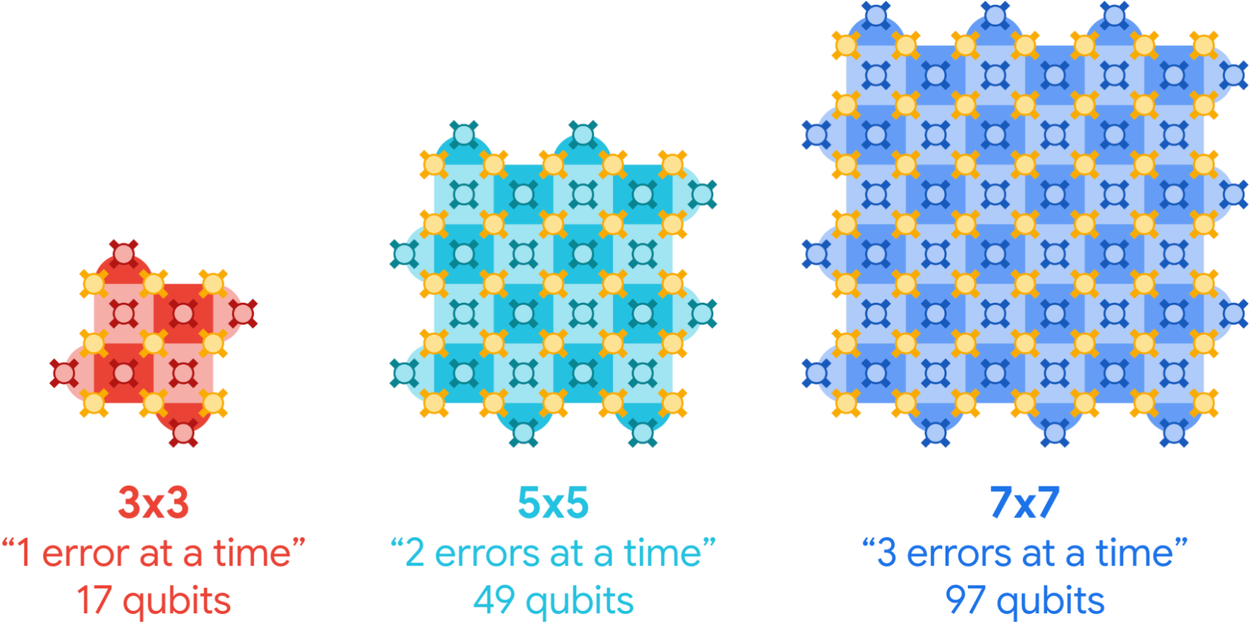
표면 코드 논리적 큐비트는 크기가 커질수록 더 많은 오류를 수정할 수 있습니다. 인코딩된 양자 상태는 데이터 큐비트(황금색) 배열에 저장됩니다. 측정 큐비트(빨강, 청록, 파랑)는 이웃한 데이터 큐비트에서 오류를 점검합니다.
그러나 여기에는 미묘한 점이 있습니다. 격자를 키우는 것이 추가 오류의 가능성도 높입니다. 만약 물리적 큐비트의 오류율이 너무 높다면, 이러한 추가 오류가 오류 수정을 압도하여 격자를 키우는 것이 오히려 성능을 저하시킵니다. 반대로 물리적 큐비트의 오류율이 충분히 낮다면 오류 수정이 이러한 추가 오류를 상쇄하며, 추가된 큐비트 수에 따라 인코딩된 오류율이 기하급수적으로 감소하게 됩니다.
이 두 가지 상황을 나누는 임계 오류율을 **임계값(threshold)**이라고 합니다. 임계값 아래에서는 양자 오류 수정이 해로운 상태에서 유용한 상태로 전환됩니다.

논리적 큐비트의 하루: 시간은 왼쪽에서 오른쪽으로 진행됩니다. 데이터 큐비트(황금색)를 초기화하고 오류를 강조하는 반복적인 패리티 검사를 수행합니다(빨강, 보라, 파랑, 초록). 마지막으로 데이터 큐비트를 측정하고 측정 데이터를 디코딩하여 오류가 수정된 논리적 측정값을 도출합니다.
Willow: 임계값을 넘어서다
오류 수정된 양자 컴퓨팅에서 "임계값 아래에서 동작하는 것"은 1990년대 초창기부터 목표로 삼아온 과제였습니다. 그러나 장치 제작, 보정, 큐비트 설계의 거의 30년간의 발전에도 불구하고 양자 컴퓨터는 여전히 이 중요한 이정표를 넘지 못했습니다. 이 상황은 최신 105큐비트 초전도 프로세서 Willow의 등장으로 달라졌습니다.
Willow는 양자 하드웨어에서의 중요한 도약을 의미합니다. 이전 아키텍처인 Sycamore의 조정 가능성을 유지하면서도 평균 큐비트 수명(T1)을 약 20μs에서 68μs ± 13μs로 개선했습니다. Willow의 큐비트와 동작은 양자 오류 수정을 염두에 두고 최적화되었으며, 최첨단 기계 학습 및 그래프 기반 알고리즘을 포함한 오류 수정 소프트웨어와 함께 실행됩니다.
Willow를 통해 우리는 표면 코드 크기를 증가시킴에 따라 기하급수적인 오류 억제를 처음으로 시연했습니다. 격자 크기를 3x3에서 5x5, 그리고 7x7로 확장할 때마다 인코딩된 오류율이 2.14배씩 감소하는 결과를 얻었습니다. 이는 최상의 물리적 큐비트 수명보다 두 배 이상 긴 수명을 가진 논리적 큐비트를 구현한 것으로, 오류 수정된 큐비트가 물리적 구성 요소의 한계를 넘어설 수 있음을 보여줍니다.
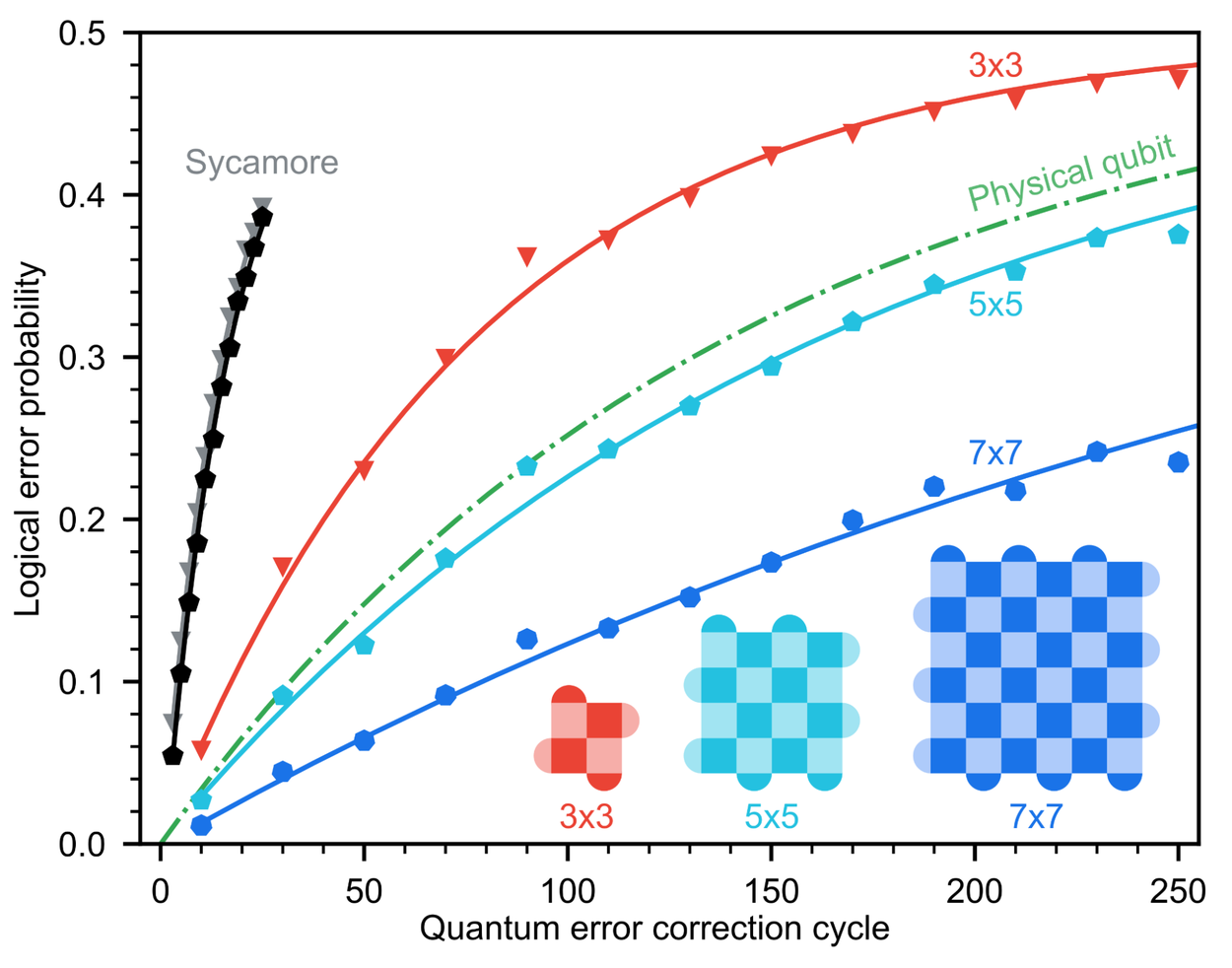
성능 스케일링: Willow의 논리적 큐비트
표면 코드 크기와 논리적 큐비트 성능 스케일링을 시각화한 결과입니다. 3x3(빨강), 5x5(청록), 7x7(파랑)으로 확장함에 따라 논리적 오류 확률이 크게 감소합니다. Willow의 7x7 논리적 큐비트는 최상의 물리적 큐비트(녹색)보다 두 배 오래 지속되며, Sycamore에서의 이전 표면 코드(회색, 검정)보다 20배 더 오래 지속됩니다.
미래를 내다보며
임계값을 넘어서면 장치의 작은 개선이 양자 오류 수정에 의해 기하급수적으로 증폭됩니다. 예를 들어, Willow의 동작 충실도가 Sycamore의 약 두 배 정도 더 우수하지만, 인코딩된 오류율은 약 20배 더 우수합니다. 이러한 급속한 개선을 기대하며, 미래의 오류 수정된 양자 컴퓨터와 관련된 다음과 같은 질문을 고민해볼 수 있습니다.
완벽에 가까운 인코딩 큐비트를 만들 수 있을까?
양자 오류 수정이 지금은 잘 작동하는 것처럼 보이지만, 오늘날의 1/1,000 오류율과 내일 필요한 1/1조 오류율 사이에는 큰 차이가 있습니다. 양자 컴퓨터 구축을 방해할 수 있는 새로운 물리적 한계가 있을까요?
이 질문에 답하기 위해 우리는 반복 코드(repetition code)를 설계합니다. 반복 코드는 모든 (지역적) 양자 오류를 방어하는 표면 코드와는 달리, 비트플립(bitflip) 오류에만 초점을 맞추지만 이를 훨씬 효율적으로 수행합니다. 반복 코드를 사용해 다른 오류 유형을 무시하는 실험을 수행하면, 표면 코드와 유사한 오류 수정 원칙을 적용하면서도 더 낮은 인코딩 오류율을 달성할 수 있습니다. 반복 코드는 우리가 궁극적으로 필요로 하는 완벽에 가까운 오류율로 오류 수정을 계속 작동시킬 수 있는지를 미리 탐색하는 역할을 합니다.
Willow에서 반복 코드를 실행하면 약 100억 사이클 동안 오류 없이 오류 수정을 수행할 수 있었습니다. 비록 비트플립 오류만 보호하더라도, 이 수준의 제어를 달성하는 것은 매우 고무적인 일입니다. 그러나 한계점도 존재합니다. 코드 크기를 늘려 인코딩 오류율을 더 낮추려고 해도 더 이상 줄어들지 않는 지점에 도달합니다. 이 현상의 원인은 현재 조사 중이며, 우리는 이를 해결할 수 있다고 확신합니다. 이는 과거 Sycamore에서 고에너지 방사선 문제를 해결했던 방식과 유사합니다.

반복 코드 성능 스케일링
반복 코드 크기에 따른 성능 스케일링을 보여줍니다. Sycamore와 비교하여 10,000배 개선을 달성했지만, 논리적 오류율이 사이클당 약 10^ 근처에서 멈추는 오류 바닥(error floor)을 관찰했습니다.
오류 수정된 양자 컴퓨터의 속도를 높일 수 있을까?
지금 이 블로그를 읽고 있는 기기가 기가헤르츠(GHz) 주파수를 가진 장치라면, 오류 수정된 양자 컴퓨터는 사실 꽤 느립니다. 가장 빠른 큐비트 기술 중 하나인 초전도 양자 컴퓨터조차도 측정 시간이 약 1마이크로초입니다. 반면, 고전적인 연산의 하위 나노초(nanosecond) 시간 범위는 양자 컴퓨터보다 천 배 이상 빠릅니다.
양자 오류 수정된 연산은 더 느릴 수 있는데, 이는 우리가 오류를 식별하기 위해 측정값을 해석해야 하기 때문입니다. 이 과정은 **양자 오류 디코더(quantum error decoder)**라는 고전 소프트웨어를 통해 이루어지며, 양자 컴퓨터가 생성하는 속도로 측정 정보를 처리해야 합니다.
초전도 큐비트 기술로는 처음으로, 장치와 함께 실시간으로 측정 정보를 디코딩할 수 있는 능력을 시연했습니다. 이는 매우 고무적인 소식이지만, 약간의 제약이 있습니다. 디코딩이 장치와 동기화되더라도 특정 오류 수정 연산에서는 디코더가 성능을 저하시킬 수 있습니다. Willow 장치에서 디코더의 지연 시간이 50~100마이크로초로 측정되었으며, 격자 크기가 커질수록 이 지연 시간이 증가할 것으로 예상됩니다. 이 지연은 오류 수정된 연산의 속도에 심각한 영향을 미칠 수 있으며, 양자 컴퓨터가 과학적 발견을 위한 실질적인 도구가 되려면 이를 개선해야 합니다.
다음 단계는?
오류 수정 기술로 원칙적으로는 완벽에 가까운 양자 컴퓨팅을 실현하기 위해 시스템을 확장할 수 있게 되었습니다. 그러나 현실적으로는 쉽지 않습니다. 대규모, 결함 허용(fault-tolerant) 양자 컴퓨터를 구축하려면 여전히 갈 길이 멉니다.
https://storage.googleapis.com/gweb-research2023-media/media/QuantumHW5-OperationsHero.mp4
점점 더 나은 프로세서에서 논리적 큐비트를 실행하며, 물리적 큐비트를 2배로 늘리고 크기를 점진적으로 키워나갑니다. 빨간색과 파란색 사각형은 인근 오류를 나타내는 패리티 검사입니다. 프로세서는 각각 약 50, 10^3, 10^6, 10^12 사이클을 안정적으로 실행할 수 있습니다.
현재 물리적 오류율에서, 상대적으로 낮은 인코딩 오류율(10^-6)을 실현하려면 표면 코드 격자(grid)당 천 개 이상의 물리적 큐비트가 필요할 수 있습니다. 또한, 이러한 모든 성과는 105큐비트 프로세서에서 이루어졌습니다. 그렇다면 1,000큐비트 프로세서에서도 같은 성능을 달성할 수 있을까요? 백만 큐비트 프로세서는 어떨까요? 앞으로 직면한 엔지니어링 과제는 막대합니다.
한편으로, 발전 속도는 놀라울 정도로 빠르며, 양자 오류 수정이 제공하는 개선은 기하급수적입니다. 작년 이후 인코딩된 성능이 20배 향상되었습니다. 대규모 양자 알고리즘을 실행하려면 얼마나 더 많은 20배 단계가 필요할까요? 아마도 생각보다 적을 수도 있습니다.
협력을 강화하고 발전을 가속화하기 위해, 우리는 연구자, 엔지니어, 개발자들이 이 여정에 동참하도록 초대합니다. 이를 위해 오픈 소스 소프트웨어와 교육 자료, 그리고 양자 오류 수정에 특화된 새로운 무료 Coursera 과정을 제공합니다.
태그:
- 알고리즘 및 이론
- 하드웨어 및 아키텍처
- 양자
'소식' 카테고리의 다른 글
| Veo 2 (1) | 2024.12.18 |
|---|---|
| 엘론 머스크는 OpenAI의 영리화를 원했다 (1) | 2024.12.18 |
| Meet Willow, our state-of-the-art quantum chip (2) | 2024.12.11 |
| 오노마AI, AI와 인간 협업으로 첫 웹툰 연재 시작 (3) | 2024.12.11 |
| 라마 3.3 출시 (1) | 2024.12.11 |

