https://arxiv.org/abs/2410.01201
Were RNNs All We Needed?
The introduction of Transformers in 2017 reshaped the landscape of deep learning. Originally proposed for sequence modelling, Transformers have since achieved widespread success across various domains. However, the scalability limitations of Transformers -
arxiv.org
초록
2017년 Transformer의 등장은 딥러닝의 전반적인 지형을 크게 바꾸어 놓았습니다. 원래는 시퀀스 모델링을 위해 고안되었지만, 이후 다양한 분야에서 폭넓은 성공을 거두었죠. 하지만 Transformer의 확장성, 특히 시퀀스 길이에 대한 제한으로 인해, 훈련 시 병렬화가 가능하면서도 유사한 성능을 내고 더욱 효율적으로 확장할 수 있는 새로운 순환 구조에 대한 관심이 다시금 부상하고 있습니다.
이 연구에서 우리는 Transformer가 등장하기 전, 무려 20년 동안 시퀀스 모델링 분야를 이끌었던 순환신경망(RNN)에 대한 역사적 관점을 재조명합니다. 구체적으로, 1997년에 발표된 LSTM과 2014년에 발표된 GRU를 살펴보며, 이 모델들을 단순화함으로써 (1) 전통적인 버전보다 더 적은 매개변수를 사용하고, (2) 훈련 과정에서 완전히 병렬화가 가능하며, (3) 다양한 과제에서 Transformer를 포함한 최신 모델과 견줄 만한 놀라운 성능을 보이는 미니멀 버전(‘minLSTM’과 ‘minGRU’)을 도출할 수 있음을 보입니다.
1 서론
1990년대부터는 Elman(1990)의 순환신경망(RNN) 계보에 속하는 Long Short-Term Memory(LSTM; Hochreiter & Schmidhuber, 1997)나 이후 제안된 Gated Recurrent Units(GRUs; Cho et al., 2014) 등이 기계 번역이나 텍스트 생성과 같은 시퀀스 모델링 작업에서 표준적인 방법으로 자리 잡아 왔습니다. 하지만 순차적으로 계산을 수행하는 특성으로 인해 병렬화가 어려워, 긴 시퀀스를 다루는 과정에서 계산 효율이 떨어지고 학습 시간이 너무 오래 걸린다는 문제가 있었습니다. 이는 실제 응용 사례에서도 흔히 직면하는 도전 과제이기도 합니다.
2017년 Vaswani 외(2017)가 제안한 Transformer는 자기어텐션(self-attention)을 통해 병렬적인 학습 메커니즘을 제공함으로써 딥러닝에 혁신을 몰고 왔습니다. 이는 시퀀스 모델링 분야에서 즉각적인 성공을 거두었을 뿐 아니라, 대형 언어 모델의 발전을 이끌었고 컴퓨터 비전(Dosovitskiy et al., 2021), 강화학습(Chen et al., 2021), 생물정보학(Jumper et al., 2021) 등 여러 영역으로 빠르게 확장되었습니다. 하지만 자기어텐션은 토큰 간 상호작용을 효율적으로 학습하게 하는 대신, 연산 복잡도가 이차적으로 증가하여 긴 시퀀스를 다루기에는 비용이 매우 커질 수 있습니다. 특히 자원이 제한된 환경에서는 그 부담이 더욱 크게 다가옵니다. 이러한 문제를 해결하기 위해, 희소화(Kitaev et al., 2019), 저계수 근사(Wang et al., 2020), 타일링(tiling; Dao et al., 2022) 등 Transformer의 효율성을 향상하려는 다양한 방법이 연구되었습니다.
최근 Transformer가 지니는 확장성 한계가 다시금 주목받으면서, 이 문제를 해결할 수 있는 대안으로 병렬화 가능하고 확장성도 뛰어난 새로운 유형의 순환 모델에 대한 관심이 높아지고 있습니다. 이 분야에서는 상태공간 모델(Gu et al., 2021), 선형화된 어텐션(Peng et al., 2023), 그리고 더 최근에는 선형 순환신경망(Orvieto et al., 2023) 등 유망한 방법들이 등장했습니다. 특히 최신 순환 모델들은 입력 의존적인 전이(input-dependent transition) 구조를 사용하며, Transformer 못지않은 성능을 입증하고 있습니다. 이들은 대형 언어 모델에 대한 확장 가능성을 보여줄 뿐 아니라, 이미지(Zhu et al., 2024a)와 그래프 기반 데이터(Wang et al., 2024a)와 같은 다른 분야로도 확장되고 있습니다.
본 연구에서는 Transformer가 부상하기 전, 무려 20년간 시퀀스 모델링 분야를 지배했던 RNN을 역사적인 맥락에서 재조명하려 합니다. 구체적으로, 입력 의존적인 순환 모델의 초기 사례인 LSTM(1997)과 GRU(2014)에 주목합니다. 그리고 이들의 게이트에서 과거 상태에 대한 의존성을 제거하면, 훈련 과정에서 병렬화를 달성할 수 있음을 보입니다. 더 나아가 이러한 단순화를 극단까지 밀어붙여 minLSTM과 minGRU라는 최소 형태를 도출할 수 있는데, 이는 (1) 기존 구조보다 적은 매개변수를 사용하고, (2) 훈련 시 완벽한 병렬화를 지원하며, (3) 단순함에도 불구하고 다양한 작업에서 놀라울 만큼 강력한 성능을 보임으로써, 최근 커뮤니티에서 강조되어 온 복잡한 구조와 알고리즘으로의 확장 경향에 도전장을 내밀고 있습니다. 부록에서는 minGRU와 minLSTM을 몇 줄의 PyTorch 코드로 구현한 예시를 제시하여, 이 모델들이 얼마나 가볍고 초심자나 실무자, 연구자들에게 쉽게 적용 가능한지 보여 드립니다.
2 배경
이 장에서는 전통적인 순환신경망(RNN)에 대해 살펴봅니다. RNN은 시계열 단계마다 은닉 상태(hidden state)를 유지하여 시간적 의존성을 포착하는 시퀀스 모델입니다. 이러한 특성 때문에, 시계열 예측이나 자연어 처리처럼 이전 단계의 맥락이 현재 예측에 중요한 영향을 미치는 작업에 특히 잘 맞습니다. 그러나 Vanilla RNN(Elman, 1990)은 기울기 소실(vanishing gradients)과 폭발(exploding gradients) 문제로 인해 장기 의존성(long-term dependency)을 학습하는 데 한계가 있습니다.
2.1 LSTM
이러한 문제를 해결하기 위해, Hochreiter & Schmidhuber(1997)는 Long Short-Term Memory(LSTM) 네트워크를 제안했습니다. LSTM은 기울기 소실 문제를 완화하도록 특별히 설계된, 매우 성공적인 형태의 RNN으로서 모델이 장기 의존성을 효과적으로 학습할 수 있게 해 줍니다. LSTM은 다음과 같이 계산됩니다:
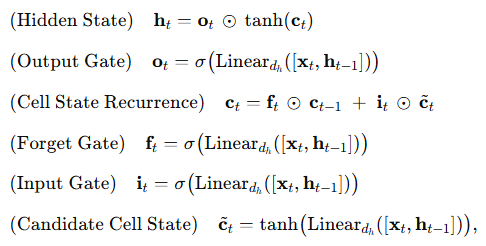

2.2 GRU
LSTM을 간소화한 방법으로, Cho 외(2014)는 Gated Recurrent Unit(GRU)을 제안했습니다. GRU는 LSTM의 세 개 게이트와 두 개 상태(은닉 상태와 셀 상태) 대신, 두 개의 게이트와 하나의 상태(은닉 상태)만을 사용합니다. 이런 단순화로 인해 GRU는 학습과 추론 속도가 더 빠르면서도 여러 작업에서 경쟁력 있는 성능을 발휘할 수 있습니다. GRU는 다음과 같이 계산됩니다:
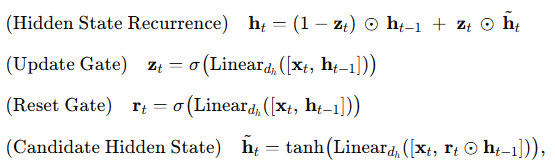

2.3 병렬 스캔(Parallel Scan)
이러한 제약으로 인해, 2017년에 Transformer가 제안되면서 기존의 LSTM과 GRU를 대체하는 시퀀스 모델링 분야의 사실상 표준 기법으로 자리 잡게 되었고, 이로써 분야 전반에 혁신이 일어났습니다. Transformer는 학습 과정에서 병렬화를 활용함으로써 전통적인 순환 모델이 안고 있던 순차적 병목(sequential bottleneck)을 해소했습니다. 그러나 동시에 시퀀스 길이에 대해 연산 복잡도가 이차적으로 증가하므로, 자원이 제한된 환경에서는 매우 긴 문맥을 처리하기가 어려운 문제가 새롭게 부각되었습니다.
이 문제를 해결하기 위해, 최근에는 Transformer에 대안을 제시하는 새로운 유형의 순환 기반 시퀀스 모델들이 다시금 주목받고 있습니다. 이들 모델은 병렬 학습이 가능하면서도 기존 RNN(LSTM, GRU 등)이 겪던 시간 역전파(BPTT) 문제를 피할 수 있고, Transformer에 필적하는 성능을 달성합니다. 특히 여러 혁신적인 모델 아키텍처들은 병렬 학습 효율을 높이기 위해 병렬 프리픽스 스캔 알고리즘(Parallel Prefix Scan; Blelloch, 1990)에 의존하고 있습니다.

3 방법론
흥미롭게도 GRU의 은닉 상태와 LSTM의 셀 상태에서 일어나는 재귀(recurrence)는 벡터 기반 표현과 닮아 있습니다. 이번 장에서는 다양한 게이트가 과거 상태에 의존하는 부분을 제거함으로써, GRU와 LSTM을 병렬 스캔(Parallel Scan)을 통해 학습할 수 있음을 보이고자 합니다. 더 나아가, tanh\tanh 등 출력 범위를 제한하는 요소를 제거해 이들 RNN을 한층 더 단순화합니다. 이러한 단계를 결합하면, 병렬 학습이 가능한 최소 형태의 GRU와 LSTM(이를 minGRUs와 minLSTMs라고 칭함)을 정의할 수 있습니다.
3.1 최소형 GRU: minGRU
3.1.1 단계 1: 게이트에서 이전 상태 의존성 제거하기
우선 GRU의 은닉 상태가 다음과 같이 업데이트되는 재귀 방식을 다시 살펴봅시다:

이는 앞서 설명한 병렬 스캔의 벡터 형태

와 닮아 있습니다. 여기서

로 매핑할 수 있죠. 하지만

와

는 각각





물론 이전 상태 의존성이 없다는 점에 대한 이론적 우려(Merrill et al., 2024)도 있지만, xLSTM(Beck et al., 2024)이나 Mamba(Gu & Dao, 2024)와 같이 이러한 의존성을 제거한 모델이 효과적이라는 실증적 근거도 상당합니다. 즉, 과거 상태를 명시적으로 참조하지 않더라도, 여러 계층을 쌓는 방식으로 장기 의존성을 학습할 수 있다는 것입니다. 실제로 xLSTM 논문을 보면, 은닉 상태 의존성을 완전히 없앤 완전 병렬화 버전(xLSTM[1:0])이 이전 상태 의존성을 유지한 버전(xLSTM[7:1])과 비슷하거나, 어떤 경우에는 더 나은 성능을 보이기도 했습니다.
3.1.2 단계 2: 후보 상태 범위 제한 없애기

3.1.3 minGRU
앞서 설명한 두 가지 단순화 단계를 결합하면, GRU의 최소 형태(minGRU)가 탄생합니다.


게다가 간소화된 GRU는 병렬 프리픽스 스캔 알고리즘을 사용해 병렬 학습할 수 있어, 시간 역전파(BPTT)가 더 이상 필요하지 않습니다. 자세한 의사코드와 간단한 PyTorch 구현은 부록에 제시되어 있습니다.
3.2 최소형 LSTM: minLSTM
3.2.1 단계 1: 게이트에서 이전 상태 의존성 제거하기
먼저, LSTM의 셀 상태가 다음과 같이 업데이트되는 재귀 과정을 다시 살펴봅시다:

이는 GRU의 은닉 상태 재귀와 유사하게, 다음 벡터 형태의 병렬 스캔 공식


3.2.2 단계 2: 후보 상태의 범위 제한 없애기

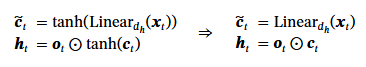
3.2.3 단계 3: 출력 스케일 단순화하기


시퀀스 모델링 작업(예: 텍스트 생성)에서는 최적화 대상(또는 타깃)이 시간에 따라 크기가 달라지지 않는(time-independent) 경우가 많습니다. LSTM의 셀 상태 업데이트 식



3.2.4 minLSTM
위의 세 단계를 결합하면, 최소 형태의 LSTM(minLSTM)을 얻을 수 있습니다:



게다가 단순화된 LSTM은 병렬 프리픽스 스캔 알고리즘을 통해 병렬로 학습할 수 있어, 더 이상 시간 역전파(BPTT)가 필요하지 않습니다. 자세한 의사코드와 간단한 PyTorch 구현은 부록에 실려 있습니다.
4 RNN으로 충분했을까?
이 장에서는 최소 형태의 LSTM(minLSTM)과 GRU(minGRU) 모델을, 전통적인 LSTM·GRU 및 현대적인 시퀀스 모델들과 비교합니다. 자세한 실험 환경 정보와 함께 의사코드 및 PyTorch 구현 코드는 부록에 수록되어 있습니다.
4.1 최소형 LSTM과 GRU의 효율성
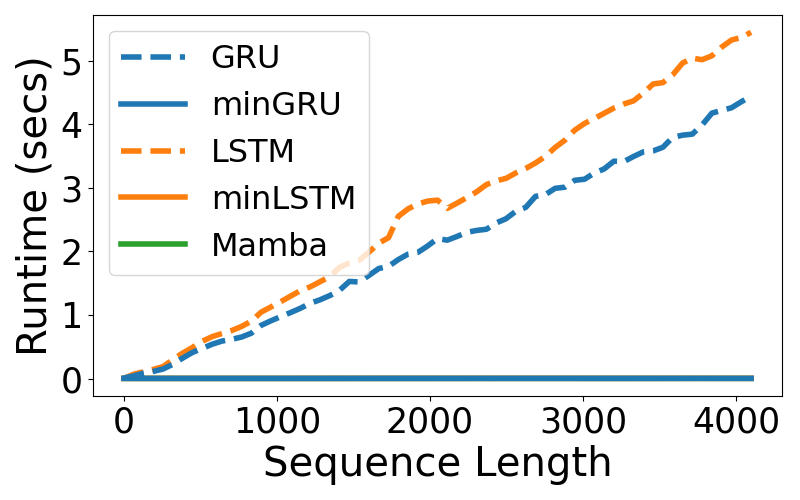


그림 1: T4 GPU에서 배치 크기 64로 학습 시 걸리는 런타임(왼쪽), 속도 향상률(중간), 메모리 사용량(오른쪽)을 보여줍니다. 왼쪽 그래프에서 minGRU, minLSTM, Mamba의 곡선은 서로 거의 겹칩니다. 이는 이들 모델이 학습 시점에서 대체로 동일한 런타임을 보인다는 의미입니다.
전통적인 순환 모델은 테스트 시점에는 일반적으로 순차적으로 계산을 진행하기 때문에 추론 자체는 비교적 효율적입니다. 하지만 전통 RNN의 가장 큰 병목 지점은 학습 시점으로, 시간 역전파(BPTT)로 인해 시퀀스 길이에 선형적으로 비례하는 학습 시간이 필요합니다. 이러한 비효율성은 RNN 기반 모델들이 결국 도태되는 한 원인이 되었습니다.
본 절에서는 전통 RNN(LSTM, GRU), 간소화된 RNN(minLSTM, minGRU)^3, 그리고 최근 주목받는 순환 모델인 Mamba(공식 구현 사용)의 학습 자원 요구량을 비교합니다.

이 실험에서는 시퀀스 길이를 달리하면서도 배치 크기는 64로 고정하였습니다. 순전파(forward pass)부터 손실(loss) 계산, 그리고 역전파(backpropagation)로 기울기를 구하는 데 소요되는 전체 런타임과 메모리 사용량을 측정했습니다. 모든 모델은 공정하고 직접적인 비교를 위해 동일한 레이어 수로 테스트했습니다.
런타임
하드웨어와 구현 방식에 따라 추론 속도는 달라질 수 있다는 점을 유의해야 합니다. 예를 들어, PyTorch 내부에 내장된 RNN은 GPU에 최적화된 저수준 구현이 이루어져 있습니다. 보다 공정한 비교를 위해, 본 실험에서는 minGRU·minLSTM·GRU·LSTM 모두를 PyTorch의 일반 연산으로 구현했습니다.
런타임 측면(그림 1 왼쪽)에서 보면, 간소화된 LSTM과 GRU(minLSTM, minGRU), 그리고 Mamba는 비슷한 수행 시간을 보입니다. 100회를 반복 측정했을 때, 시퀀스 길이가 512일 때 minLSTM, minGRU, Mamba의 런타임은 각각 2.97ms, 2.72ms, 2.71ms였고, 시퀀스 길이가 4096인 경우에는 각각 3.41ms, 3.25ms, 3.15ms로 나타났습니다. 반면 전통적인 RNN(LSTM, GRU)은 시퀀스 길이에 대해 선형적으로 런타임이 증가했습니다. 예컨대 시퀀스 길이가 512일 때 minGRU와 minLSTM은 T4 GPU 기준 GRU와 LSTM보다 각각 175배, 235배 더 빠른 학습 시간을 보였고(그림 1 중간), 시퀀스 길이가 4096으로 늘어나면 그 격차는 1324배, 1361배까지 벌어졌습니다. 즉, minGRU로 하루 만에 끝날 학습을 전통 GRU로 진행할 경우 3년 이상 걸릴 수도 있다는 뜻입니다.
메모리
병렬 스캔(Parallel Scan) 알고리즘을 사용해 출력을 병렬로 효율적으로 계산할 수 있지만, 그만큼 큰 연산 그래프가 생성되므로 전통적 RNN에 비해 더 많은 메모리를 필요로 합니다(그림 1 오른쪽). 실제로 minGRU와 minLSTM은 기존 GRU와 LSTM에 비해 각각 약 88% 더 많은 메모리를 사용하며, Mamba는 minGRU에 비해 약 56% 더 많은 메모리를 사용합니다. 하지만 RNN 학습에서 실제 병목은 대개 런타임이라는 점에서, 실무 환경에서는 이 메모리 사용량 증가가 상대적으로 덜 치명적일 수 있습니다.

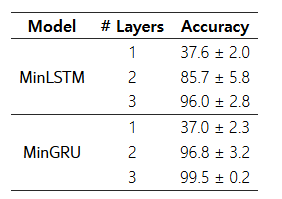
표 1: Mamba 논문(Gu & Dao, 2024)에 나온 Selective Copying Task에서 레이어 수를 달리하며 측정한 결과.

표 1은 Mamba 논문에서 제시된 Selective Copying Task에 대해 레이어 수를 변화시키면서 성능을 비교한 결과입니다. 레이어가 2개 이상이 되면 성능이 급격히 향상되는 것을 보면, 시간 종속성이 생기는 효과가 즉각적으로 드러나는 것을 확인할 수 있습니다.
학습 안정성
레이어가 늘어날수록 정확도의 분산이 줄어들어 학습이 좀 더 안정적이 된다는 점도 함께 관찰됩니다(표 1). 또한 minLSTM과 minGRU가 모두 Selective Copying Task를 풀어내긴 했지만, 실제로는 minGRU가 더 안정적인 경향을 보였고 분산도 더 낮았습니다. minLSTM은 이전 정보를 “버리는”(forget) 비율과 새 정보를 “추가하는”(input) 비율을 따로 제어(망각 게이트와 입력 게이트)하기 때문에 학습 과정에서 두 집합의 파라미터가 다른 방향으로 튜닝되면서 최적의 비율을 찾기 다소 까다로울 수 있습니다. 반면 minGRU는 한 집합의 파라미터(업데이트 게이트)만으로 이전 정보와 신규 정보를 조절하므로, 학습 과정에서 더 간단하고 안정적으로 동작합니다.
4.2 최소형 RNN의 놀라운 성능
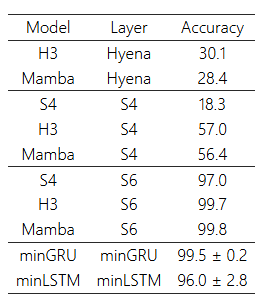
표 2: 선택적 복사(Selective Copy) 과제 성능. minLSTM, minGRU, 그리고 Mamba의 S6(Gu & Dao, 2024)는 이 과제를 성공적으로 해결했습니다. 그 외 모델(S4, H3, Hyena)은 최대한 잘해도 이 과제를 부분적으로만 해결할 수 있었습니다.
이번 장에서는 1990년대 말~2010년대 초반에 제안된 전통 모델인 LSTM(1997)과 GRU(2014)를 극도로 단순화한 버전(minLSTM, minGRU)과, 최근 제안된 여러 현대적 시퀀스 모델들을 비교한 결과를 살펴봅니다. 본 연구의 주요 목표는 특정 과제에서 최고 성능을 달성하는 것이 아니라, 전통적 구조를 단순화해도 최신 시퀀스 모델과 맞먹는 경쟁력 있는 결과를 낼 수 있음을 보이는 데 있습니다.
선택적 복사(Selective Copy)
먼저, Mamba 논문(Gu & Dao, 2024)에서 소개된 선택적 복사(Selective Copy) 과제를 살펴봅시다. 이 과제는 S4(Gu et al., 2021), Hyena(Poli et al., 2023) 등 기존 최첨단(state-of-the-art) 모델들에 비해 Mamba의 상태공간 모델(S6)이 얼마나 성능이 향상되었는지를 보여주는 핵심 지표로 사용된 바 있습니다. 이 과제에서는 모델이 불필요한 토큰은 거르고, 필요한 토큰만 기억해야 하는 콘텐츠 기반 추론(content-aware reasoning)이 요구됩니다.
표 2에서 S4, H3(Fu et al., 2023), Hyena, Mamba(S6)와 더불어 병렬 학습이 가능한 간소화된 LSTM·GRU(minLSTM, minGRU)를 비교했습니다. 참고로 이들 모델의 결과값은 Mamba 논문에 제시된 수치를 그대로 인용했습니다. 그중 오직 Mamba의 S6 모델만이 완벽에 가까운 성능으로 과제를 해결하고 있습니다.
그러나 minLSTM과 minGRU도 이 선택적 복사 과제를 무난히 해결해 S6와 비슷한 성능을 달성했으며, 다른 최신 기법(S4, H3, Hyena)들을 웃도는 결과를 보였습니다. 이는 콘텐츠 인식적 게이트(Content-aware gating) 메커니즘을 사용하는, 전통 LSTM과 GRU 계열 모델의 효용성을 재조명해 주는 증거라 할 수 있습니다.

표 3: D4RL(Fu et al., 2020) 데이터셋의 강화학습 실험 결과. Decision Transformer(Chen et al., 2021) 방식에 따라 전문가 기준 보상을 정규화하여(값이 높을수록 좋음), 다섯 가지 시드에 대한 평균을 보고합니다. 간소화된 LSTM·GRU(minLSTM, minGRU)는 Decision S4(David et al., 2023)를 뛰어넘고, Decision Transformer, Aaren(Feng et al., 2024), Mamba(Ota, 2024)와 비슷한 수준의 성능을 냅니다.
강화학습
다음으로는 D4RL 벤치마크(Fu et al., 2020)에 포함된 MuJoCo 로코모션 과제들을 살펴봅니다. HalfCheetah, Hopper, Walker 세 가지 환경 각각에 대해, 데이터 품질이 서로 다른 Medium(M), Medium-Replay(M-R), Medium-Expert(M-E) 세 개의 데이터셋을 활용했습니다.
표 3에서 minLSTM과 minGRU를, 기존의 여러 Decision Transformer 파생 모델들과 비교했습니다. 여기에는 원본 Decision Transformer(DT; Chen et al., 2021), Decision S4(DS4; David et al., 2023), Decision Mamba(Ota, 2024), (Decision) Aaren(Feng et al., 2024) 등이 포함됩니다. 이들의 결과값은 Decision Mamba 및 Aaren 논문에서 인용했습니다.
실험 결과, minLSTM과 minGRU는 Decision S4보다 좋은 성능을 보였고, Decision Transformer, Aaren, Mamba와 견줄 만한 성능을 냈습니다. Decision S4는 순환 구조임에도 입력 의존적(input-aware)인 전이(transition)를 사용하지 않기 때문에, 성능이 떨어지는 것으로 보입니다. 9개(3×3) 데이터셋 전체의 평균 성능을 보면, minLSTM과 minGRU는 Decision Mamba와 매우 근소한 차이를 보이며, 그 외 모델들에 대해서는 우수한 성적을 거두었습니다.

그림 2: Shakespeare 데이터셋의 언어 모델링 결과. 10여 년 이상 된 RNN 계열 모델(LSTM, GRU)의 최소형 버전도 Mamba와 Transformer에 견줄 만한 성능을 보이고 있습니다. Transformer는 유사 성능을 내기 위해 약 2.5배 더 많은 학습 단계를 거쳤고, 최종적으로는 과적합(overfitting)이 일어났습니다.
언어 모델링
마지막으로는 언어 모델링 과제를 살펴봅니다. Shakespeare 원문을 문자 단위(character-level)로 처리하는 GPT 모델을 nanoGPT(Karpathy, 2022) 프레임워크를 사용해 학습했습니다. 그림 2는 minLSTM, minGRU, Mamba, Transformer를 비교한 결과(크로스 엔트로피 손실 곡선)를 나타냅니다.
결과적으로 minGRU, minLSTM, Mamba, Transformer는 각각 1.548, 1.555, 1.575, 1.547의 유사한 테스트 손실값을 달성했습니다. Mamba는 다른 모델들보다 성능이 다소 낮았지만, 특히 초기 단계에서 빠르게 학습을 진행하여 400 스텝에서 베스트 성능에 도달했습니다. 반면 minGRU와 minLSTM은 각각 575 스텝, 625 스텝까지 학습해야 최고 성능에 도달했습니다. Transformer는 이와 비슷한 성능을 내기 위해 2000 스텝(minGRU 대비 약 2.5배)을 소비했으며, 이는 학습 속도는 물론 자원 소모 측면에서 상당한 부담을 안깁니다(시퀀스 길이에 대해 이차적 복잡도를 가지기 때문).
5. 관련 연구
이 장에서는 확장성 측면에서 Transformer보다 더 우수하면서도, 경험적으로는 Transformer에 견줄 만한 강력한 성능을 보이는 최근의 효율적인 순환 시퀀스 모델들을 간략히 살펴봅니다. 효율적인 순환 모델의 부활과 관련해 보다 종합적인 논의를 원하신다면, 최근 서베이(Tiezzi et al., 2024)를 참고하길 권합니다. 전반적으로, 이러한 모델들은 크게 세 방향에서 발전하고 있습니다.
(딥) 상태공간 모델(SSM)
연속시간 선형 시스템(continuous-time linear systems)을 기반으로, Gu et al.(2021)은 S4라는 상태공간 모델을 제안했습니다. S4는 추론 시에는 RNN처럼 펼쳐서(unroll) 사용할 수 있고, 훈련 시에는 합성곱 신경망과 유사한 방식으로 학습할 수 있습니다. S4의 성공 이후, 이 분야는 비약적으로 발전하며(Gu et al., 2022; Gupta et al., 2022; Hasani et al., 2023; Smith et al., 2023) 자연어 처리(Mehta et al., 2023)나 오디오 분석(Goel et al., 2022) 등 다양한 영역에 적용되어 왔습니다.
최근에는 Mamba가 SSM 분야에서 중요한 도약을 이룬 사례로 부상했는데, 기존 모델들과 달리 입력에 따라 전이 행렬(transition matrix)이 달라지는 S6라는 상태공간 모델을 제안해 큰 주목을 받았습니다. 이전 모델들은 입력에 독립적인 전이 행렬을 사용했다는 점과 대조적이죠. Mamba 및 다른 상태공간 모델들의 성공 덕분에, 이에 대한 서베이 논문도 다수 발간되었습니다(Wang et al., 2024b; Patro & Agneeswaran, 2024; Qu et al., 2024).
어텐션의 순환 버전
또 다른 대표적 연구 흐름은 선형 어텐션(linear attention; Katharopoulos et al., 2020)에 관한 것입니다. 예컨대 Sun et al.(2023)과 Qin et al.(2023)은 입력에 독립적인 게이트(감쇠 계수, decay factor)를 사용하는 선형 어텐션 모델을 제안했습니다. 반면 Katsch(2023)와 Yang et al.(2024)은 입력에 의존적인 게이트를 사용하는 선형 어텐션 변형 모델을 선보였습니다. 최근에는 Feng et al.(2024)가 소프트맥스(softmax) 어텐션 역시 RNN의 한 형태로 해석할 수 있음을 보이고, 이를 바탕으로 한 순환 모델을 제안하기도 했습니다.
병렬화 가능한 RNN
본 연구는 RNN을 병렬화하는 여러 선행 연구들과 밀접한 관련이 있습니다. 예컨대, Bradbury et al.(2017)은 고전적인 게이트 기반 RNN을 변형하여 효율을 위해 합성곱 레이어를 도입하고, 이를 시간축 방향으로 적용하는 방식을 제안했습니다. Martin & Cundy(2018)은 선형 의존성을 갖는 RNN은 병렬 스캔(Parallel Scan)을 통해 효율적으로 학습할 수 있음을 시연했습니다. 이를 기반으로 저자들은 GILR이라는 게이트 기반 선형 RNN을 제안했는데, 이 모델의 출력은 기존 RNN(LSTM 등)의 이전 상태 의존성을 대체할 수 있어 병렬 학습이 가능해집니다. 흥미롭게도, minGRU는 활성화 함수를 제거한 버전의 GILR와 동일합니다.
최근 Orvieto et al.(2023)은 복소수 대각(linear) 재귀와 지수형 파라미터화를 사용하는 선형 게이트 RNN을 제안해, 상태공간 모델과 견줄 만한 성능을 달성했습니다. Qin et al.(2024b)는 HGRN을 발표했는데, 이 모델에서 토큰 믹서(token mixer)인 HGRU는 복소수(극좌표) 재귀, 망각 게이트의 하한(lower bound), 출력 게이트 등을 갖춘 선형 게이트 RNN 구조를 채택합니다. 이후 HGRN2(Qin et al., 2024a)는 상태 확장을 도입하여 HGRN을 개선했습니다. Beck et al.(2024)는 지수 게이팅(exponential gating)과 정규화(normalizer) 상태를 결합해 LSTM을 확장하는 xLSTM을 제안했으며, 여기에는 병렬화가 가능한 mLSTM과 순차적 계산만 가능한 sLSTM이 존재합니다. mLSTM은 은닉 상태 의존성을 제거해 병렬화를 가능케 하고, 행렬 메모리 셀(matrix memory cell)과 쿼리 벡터를 사용해 메모리에서 정보를 검색하는 구조를 사용합니다. Zhu et al.(2024b)는 HGRN에서 얻은 통찰을 토대로 GRU를 재조명하여, 병렬화가 가능하고 행렬 곱셈을 제거하며 3진(ternary) 가중치 양자화를 활용한 토큰 믹서를 제안했습니다.
6. 결론
본 연구에서는 전통적인 RNN, 특히 Transformer 모델이 부상하기 전 무려 20년에 걸쳐 시퀀스 모델링 분야를 지배해 온 LSTM(1997)과 GRU(2014)에 주목했습니다. 게이트가 이전 은닉 상태에 의존하던 부분을 제거하면 전통적 RNN을 병렬로 학습할 수 있음을 보였고, 나아가 이러한 구조를 극단까지 단순화한 minLSTM과 minGRU를 제안했습니다. 이 모델들은 (1) 기존 버전에 비해 필요한 매개변수 수가 적고, (2) 학습 시 완전히 병렬화가 가능하며, (3) 다양한 과제에서 놀라울 만큼 경쟁력 있는 성능을 보여, 간소함에도 불구하고 최신 모델에 필적하는 모습을 보였습니다. 부록에는 몇 줄의 PyTorch 코드만으로도 쉽게 구현할 수 있는 예시를 실어 두어, 초심자나 실무자, 연구자가 이 모델을 가볍게 활용할 수 있도록 했습니다. 본 논문이 시퀀스 모델링의 흐름을 다시금 되짚는 계기가 되길 바라며, 복잡한 최신 구조만이 아니라 LSTM과 GRU 같은 단순하면서도 강력한 기반 모델을 재평가해 보는 움직임이 확산되길 기대합니다. 정말로 “RNN만으로 충분했던 것이 아닐까?”라는 질문을 던지고자 합니다.
한계점(Limitations)
Mamba나 xLSTM 등의 최신 모델은 80GB 메모리가 탑재된 최신 A100 GPU에서 실험되었습니다. 반면 본 연구에서는 16GB 메모리(다른 모델 실험 환경의 약 20% 수준)만 지원되는 구형 GPU(P100, T4, Quadro 5000)에서 실험을 진행했습니다. 이런 하드웨어 제약으로 인해 대규모 실험을 수행하기 어려웠으며, 일부 과제에서는 미니배치 크기를 절반으로 줄이고 그래디언트 누적(gradient accumulation)을 사용해 학습 속도가 크게 느려지기도 했습니다.
그럼에도 이러한 제약 속에서 얻은 결론들은 대규모 설정에도 충분히 일반화될 가능성이 높다고 생각합니다. 전통 RNN의 최소형 모델들이 최근 순환 모델들과 기본적인 아이디어(예: 입력 의존 게이팅)에서 유사점을 공유하기 때문에, 더 큰 데이터셋과 충분한 계산 자원이 주어진다면 비슷한 성능 향상을 기대할 수 있을 것입니다.
부록 A 기본 버전(바닐라 버전) 구현 세부사항
본 부록에서는 minGRU와 minLSTM의 의사코드(pseudocode)와 이에 대응하는 PyTorch 코드를 제시합니다. 대부분의 순환 시퀀스 모델과 마찬가지로, 반복 곱셈이 다수 이루어지기 때문에 특히 학습 과정에서 수치적 불안정성(numerical instability)이 자주 발생합니다. 이를 개선하기 위해, 우리는 로그 스페이스 구현(부록 B 참조)을 사용하여 수치적 안정성을 높였습니다.
A.1 기본 버전(바닐라 버전) 의사코드
A.1.1 minGRU: 최소형 GRU
알고리즘 1: 순차(Sequential) 모드 – 최소형 GRU(minGRU)
입력: x_t, h_{t-1}
출력: h_t
z_t ← σ(Linear_{d_h}(x_t))
h̃_t ← Linear_{d_h}(x_t)
h_t ← (1 - z_t) ⊙ h_{t-1} + z_t ⊙ h̃_t알고리즘 2: 병렬(Parallel) 모드 – 최소형 GRU(minGRU)
입력: x_{1:t}, h_0
출력: h_{1:t}
z_{1:t} ← σ(Linear_{d_h}(x_{1:t}))
h̃_{1:t} ← Linear_{d_h}(x_{1:t})
h_{1:t} ← ParallelScan((1 - z_{1:t}), [h_0, z_{1:t} ⊙ h̃_{1:t}])
A.1.2 minLSTM: 최소형 LSTM
알고리즘 3: 순차(Sequential) 모드 – 길이 독립 스케일링(length independence scaling)을 적용한 최소형 LSTM(minLSTM)
입력: x_t, h_{t-1}
출력: h_t
f_t ← σ(Linear_{d_h}(x_t))
i_t ← σ(Linear_{d_h}(x_t))
f_t', i_t' ← f_t / (f_t + i_t), i_t / (f_t + i_t)
h̃_t ← Linear_{d_h}(x_t)
h_t ← f_t' ⊙ h_{t-1} + i_t' ⊙ h̃_t
알고리즘 4: 병렬(Parallel) 모드 – 길이 독립 스케일링(length independence scaling)을 적용한 최소형 LSTM(minLSTM)
입력: x_{1:t}, h_0
출력: h_{1:t}
f_{1:t} ← σ(Linear_{d_h}(x_{1:t}))
i_{1:t} ← σ(Linear_{d_h}(x_{1:t}))
f_{1:t}', i_{1:t}' ← f_{1:t} / (f_{1:t} + i_{1:t}), i_{1:t} / (f_{1:t} + i_{1:t})
h̃_{1:t} ← Linear_{d_h}(x_{1:t})
h_{1:t} ← ParallelScan(f_{1:t}', [h_0, i_{1:t}' ⊙ h̃_{1:t}])
A.2 PyTorch 코드: 기본(바닐라) 버전
아래는 minGRU와 minLSTM을 PyTorch로 구현한 간단한 예시입니다. 순차(Sequential) 모드와 병렬(Parallel) 모드 각각에 대한 코드를 보여 줍니다.
A.2.1 minGRU: 최소형 GRU
Listing 1: 순차(Sequential) 모드 – 최소형 GRU(minGRU)
1 def forward(self, x_t, h_prev):
2 # x_t: (batch_size, 1, input_size)
3 # h_prev: (batch_size, 1, hidden_size)
4
5 z_t = torch.sigmoid(self.linear_z(x_t))
6 h_tilde = self.linear_h(x_t)
7 h_t = (1 - z_t) * h_prev + z_t * h_tilde
8 return h_t

Listing 2: 병렬(Parallel) 모드 – 최소형 GRU(minGRU)
1 def forward(self, x, h_0):
2 # x: (batch_size, seq_len, input_size)
3 # h_0: (batch_size, 1, hidden_size)
4
5 z = torch.sigmoid(self.linear_z(x))
6 h_tilde = self.linear_h(x)
7 h = parallel_scan((1 - z),
8 torch.cat([h_0, z * h_tilde], dim=1))
9 return h

A.2.2 minLSTM: 최소형 LSTM
Listing 3: 순차(Sequential) 모드 – 길이 독립 스케일링이 적용된 최소형 LSTM(minLSTM)
1 def forward(self, x_t, h_prev):
2 # x_t: (batch_size, 1, input_size)
3 # h_prev: (batch_size, 1, hidden_size)
4
5 f_t = torch.sigmoid(self.linear_f(x_t))
6 i_t = torch.sigmoid(self.linear_i(x_t))
7 tilde_h_t = self.linear_h(x_t)
8 f_prime_t = f_t / (f_t + i_t)
9 i_prime_t = i_t / (f_t + i_t)
10 h_t = f_prime_t * h_prev + i_prime_t * tilde_h_t
11 return h_t
Listing 4: 병렬(Parallel) 모드 – 길이 독립 스케일링이 적용된 최소형 LSTM(minLSTM)
1 def forward(self, x, h_0):
2 # x: (batch_size, seq_len, input_size)
3 # h_0: (batch_size, 1, hidden_size)
4
5 f = torch.sigmoid(self.linear_f(x))
6 i = torch.sigmoid(self.linear_i(x))
7 tilde_h = self.linear_h(x)
8 f_prime = f / (f + i)
9 i_prime = i / (f + i)
10 h = parallel_scan(f_prime,
11 torch.cat([h_0, i_prime * tilde_h], dim=1))
12 return h
위의 코드들은 모두 “바닐라” 버전이며, 실제 훈련 시에는 숫자 오버플로나 언더플로 등의 수치적 불안정성을 줄이기 위해 로그 스페이스 구현(부록 B 참고)을 사용하는 것이 좋습니다.
부록 B 로그 스페이스(Log-Space) 버전 구현 세부사항 (추가적인 수치적 안정성)
이 부록에서는 수치적 안정성을 높이기 위해 minLSTM과 minGRU를 로그 스페이스(Log-Space)에서 구현하는 방법을 다룹니다. 학습 시에는 시간 역전파(BPTT)를 피하기 위해 병렬 모드를 사용하여 학습 속도를 크게 높일 수 있으며, 추론 시에는 순차 모드를 사용합니다.

Listing 5: 로그 스페이스를 이용한 병렬 스캔
1 def parallel_scan_log(log_coeffs, log_values):
2 # log_coeffs: (batch_size, seq_len, input_size)
3 # log_values: (batch_size, seq_len + 1, input_size)
4 a_star = F.pad(torch.cumsum(log_coeffs, dim=1), (0, 0, 1, 0))
5 log_h0_plus_b_star = torch.logcumsumexp(
6 log_values - a_star, dim=1)
7 log_h = a_star + log_h0_plus_b_star
8 return torch.exp(log_h)[:, 1:]

이렇게 로그 스페이스에서 계산하면, 반복적으로 곱셈이 발생하거나 매우 작은/큰 값이 누적될 때 흔히 발생하는 오버플로·언더플로 문제를 완화할 수 있습니다.
B.2 로그 스페이스(Log-Space) 버전 의사코드
추가적인 수치적 안정성을 확보하기 위해, minGRU와 minLSTM을 로그 스페이스로 다시 작성할 수 있습니다.



알고리즘 5: 순차 모드 – 로그 스페이스로 학습 가능한 최소형 GRU(minGRU)
입력: x_t, h_{t-1}
출력: h_t
z_t ← σ(Linear_{d_h}(x_t))
h̃_t ← g(Linear_{d_h}(x_t))
h_t ← (1 - z_t) ⊙ h_{t-1} + z_t ⊙ h̃_t
알고리즘 6: 병렬 모드 – 로그 스페이스로 학습하는 최소형 GRU(minGRU)
입력: x_{1:t}, h_0
출력: h_{1:t}
linear_z ← Linear_{d_h}
log_z_{1:t} ← -Softplus(linear_z(-x_{1:t}))
log_coeffs ← -Softplus(linear_z(x_{1:t}))
log_h_0 ← log(h_0)
log_h̃_{1:t} ← log_g(Linear_{d_h}(x_{1:t}))
h_{1:t} ← ParallelScanLog(
log_coeffs,
[ log_h_0, log_z_{1:t} + log_h̃_{1:t} ]
)

B.2.2 minLSTM: 최소형 LSTM



알고리즘 7: 순차(Sequential) 모드 – 길이 독립 스케일링을 적용한 최소형 LSTM(minLSTM)의 로그 스페이스 학습
입력: x_t, h_{t-1}
출력: h_t
f_t ← σ(Linear_{d_h}(x_t))
i_t ← σ(Linear_{d_h}(x_t))
f_t', i_t' ← f_t / (f_t + i_t), i_t / (f_t + i_t)
h̃_t ← g(Linear_{d_h}(x_t))
h_t ← f_t' ⊙ h_{t-1} + i_t' ⊙ h̃_t
알고리즘 8: 병렬(Parallel) 모드 – 로그 스페이스로 학습하는 길이 독립 스케일링 버전 최소형 LSTM(minLSTM)
입력: x_{1:t}, h_0
출력: h_{1:t}
diff ← Softplus(-Linear_{d_h}(x_{1:t}))
- Softplus(-Linear_{d_h}(x_{1:t}))
log_f'_{1:t} ← -Softplus(diff)
log_i'_{1:t} ← -Softplus(-diff)
log_h_0 ← log(h_0)
log_h̃_{1:t} ← log_g(Linear_{d_h}(x_{1:t}))
h_{1:t} ← ParallelScanLog(
log_f'_{1:t},
[
log_h_0,
log_i'_{1:t} + log_h̃_{1:t}
]
)

B.3 PyTorch 코드: 로그 스페이스(Log-Space) 버전
Listing 6:연속 함수 g를 통해

가 양수 값을 갖도록 보장
1 def g(x):
2 return torch.where(x >= 0, x + 0.5, torch.sigmoid(x))
3 def log_g(x):
4 return torch.where(x >= 0, (F.relu(x) + 0.5).log(),
5 -F.softplus(-x))
B.3.1 minGRU: 최소형 GRU
Listing 7: 순차(Sequential) 모드 – 로그 스페이스로 학습하는 최소형 GRU(minGRU)
1 def forward(self, x_t, h_prev):
2 # x_t: (batch_size, 1, input_size)
3 # h_prev: (batch_size, 1, hidden_size)
4
5 z = torch.sigmoid(self.linear_z(x_t))
6 h_tilde = g(self.linear_h(x_t))
7 h_t = (1 - z) * h_prev + z * h_tilde
8 return h_t

Listing 8: 병렬(Parallel) 모드 – 로그 스페이스로 학습하는 최소형 GRU(minGRU)
1 def forward(self, x, h_0):
2 # x: (batch_size, seq_len, input_size)
3 # h_0: (batch_size, 1, hidden_size)
4
5 k = self.linear_z(x)
6 log_z = -F.softplus(-k)
7 log_coeffs = -F.softplus(k)
8 log_h_0 = log_g(h_0)
9 log_tilde_h = log_g(self.linear_h(x))
10 h = parallel_scan_log(
11 log_coeffs,
12 torch.cat([log_h_0, log_z + log_tilde_h], dim=1)
13 )
14 return h

B.3.2 minLSTM: 최소형 LSTM
Listing 9: 순차(Sequential) 모드 – 로그 스페이스로 길이 독립 스케일링을 적용한 최소형 LSTM(minLSTM)
1 def forward(self, x_t, h_prev):
2 # x_t: (batch_size, 1, input_size)
3 # h_prev: (batch_size, 1, hidden_size)
4
5 f_t = torch.sigmoid(self.linear_f(x_t))
6 i_t = torch.sigmoid(self.linear_i(x_t))
7 tilde_h_t = g(self.linear_h(x_t))
8 f_prime_t = f_t / (f_t + i_t)
9 i_prime_t = i_t / (f_t + i_t)
10 h_t = f_prime_t * h_prev + i_prime_t * tilde_h_t
11 return h_t
Listing 10: 병렬(Parallel) 모드 – 로그 스페이스로 길이 독립 스케일링을 적용한 최소형 LSTM(minLSTM)
1 def forward(self, x, h_0):
2 # x: (batch_size, seq_len, input_size)
3 # h_0: (batch_size, 1, hidden_size)
4
5 diff = F.softplus(-self.linear_f(x)) \
6 - F.softplus(-self.linear_i(x))
7 log_f = -F.softplus(diff)
8 log_i = -F.softplus(-diff)
9 log_h_0 = torch.log(h_0)
10 log_tilde_h = log_g(self.linear_h(x))
11 h = parallel_scan_log(
12 log_f,
13 torch.cat([log_h_0, log_i + log_tilde_h], dim=1)
14 )
15 return h

이와 같은 로그 스페이스 구현을 통해, 긴 시퀀스에서도 오버플로·언더플로를 크게 줄이면서 안정적으로 학습할 수 있습니다. 특히 병렬(Parallel) 모드는 BPTT를 피하므로, 매우 긴 시퀀스를 다룰 때 학습 속도 면에서 큰 이점을 얻을 수 있습니다.
아래와 같이 구현되지 않을까 싶음.
import torch
import torch.nn as nn
import torch.nn.functional as F
# --------------------------------------------------
# 병렬 학습을 위한 간단한 Parallel Scan 예시 (Vanilla 버전)
# --------------------------------------------------
def parallel_scan(a, b):
"""
a: (batch_size, seq_len, hidden_size) -- 곱할 계수(1 - z 등)
b: (batch_size, seq_len+1, hidden_size) -- 더할 항(h0, z*h_tilde 등)
반환: (batch_size, seq_len, hidden_size)
간단히 앞에서부터 순차적으로 누적하는 과정을, PyTorch 연산을 통해
병렬화할 수 있다는 개념적 예시입니다.
"""
# 실제 병렬 알고리즘 구현은 여기서 더 복잡할 수 있음
h = []
# h0를 초기값으로 지정
h_prev = b[:, 0] # (batch_size, hidden_size)
seq_len = a.shape[1]
for t in range(seq_len):
h_t = a[:, t] * h_prev + b[:, t+1]
h.append(h_t.unsqueeze(1)) # shape 맞추기
h_prev = h_t
return torch.cat(h, dim=1)
# --------------------------------------------------
# 병렬 학습을 위한 간단한 Parallel Scan 예시 (Log-space 버전)
# --------------------------------------------------
def parallel_scan_log(log_coeffs, log_values):
"""
log_coeffs: log(a_{1:t})
log_values: log(b_{0:t})
여기서는 예시로, 누적합 대신 간단한 형태만 보여줍니다.
실제로는 B.1 부록에 나온 것처럼 logcumsumexp 등을 활용해야 합니다.
"""
# 아주 단순화된 예시. 실제 구현과 다를 수 있습니다!
batch_size, seq_len, hidden_size = log_coeffs.shape
h = []
# h0를 초기값으로
log_h_prev = log_values[:, 0] # (batch_size, hidden_size)
for t in range(seq_len):
# log_h_t = log( a_t * h_{t-1} + b_t )
# = log( exp(log(a_t) + log(h_{t-1})) + exp(log(b_t)) )
# 실제는 log-sum-exp로 해야 함
# 여기선 예시로 그냥 덧셈으로 대체
# !!!!! 실제 환경에서는 오버플로/언더플로 위험이 큼 !!!!!
log_h_t = torch.logaddexp(
log_coeffs[:, t] + log_h_prev,
log_values[:, t+1]
)
h.append(log_h_t.unsqueeze(1))
log_h_prev = log_h_t
return torch.cat(h, dim=1).exp() # exp()를 통해 최종 h 반환
# --------------------------------------------------
# g, log_g 함수 (양수 보장을 위해 사용)
# --------------------------------------------------
def g(x):
"""
x >= 0 일 때는 x+0.5,
x < 0 일 때는 sigmoid(x).
"""
return torch.where(x >= 0, x + 0.5, torch.sigmoid(x))
def log_g(x):
"""
g(x)를 log 스페이스에서 처리하기 위한 함수.
x >= 0 이면 log(x+0.5),
x < 0 이면 -softplus(-x) [= log(sigmoid(x))]
"""
return torch.where(
x >= 0,
(F.relu(x) + 0.5).log(),
-F.softplus(-x)
)
# --------------------------------------------------
# 1. minGRU 클래스 구현
# --------------------------------------------------
class MinGRU_Sequential(nn.Module):
"""
순차(Sequential) 버전 minGRU
"""
def __init__(self, input_size, hidden_size):
super().__init__()
self.linear_z = nn.Linear(input_size, hidden_size)
self.linear_h = nn.Linear(input_size, hidden_size)
def forward(self, x_t, h_prev):
# x_t: (batch_size, 1, input_size)
# h_prev: (batch_size, 1, hidden_size)
z = torch.sigmoid(self.linear_z(x_t))
h_tilde = self.linear_h(x_t)
h_t = (1 - z) * h_prev + z * h_tilde
return h_t
class MinGRU_Parallel(nn.Module):
"""
병렬(Parallel) 버전 minGRU (Vanilla 버전)
"""
def __init__(self, input_size, hidden_size):
super().__init__()
self.linear_z = nn.Linear(input_size, hidden_size)
self.linear_h = nn.Linear(input_size, hidden_size)
def forward(self, x, h_0):
# x: (batch_size, seq_len, input_size)
# h_0: (batch_size, 1, hidden_size)
z = torch.sigmoid(self.linear_z(x)) # (B, T, H)
h_tilde = self.linear_h(x) # (B, T, H)
# parallel_scan의 입력 맞추기
# coeff = (1 - z)
# b = cat([h0, z*h_tilde], dim=1)
coeff = (1 - z)
b = torch.cat([h_0, z * h_tilde], dim=1) # b.shape: (B, T+1, H)
return parallel_scan(coeff, b)
class MinGRU_ParallelLog(nn.Module):
"""
병렬(Parallel) 버전 minGRU (Log-space 버전)
"""
def __init__(self, input_size, hidden_size):
super().__init__()
self.linear_z = nn.Linear(input_size, hidden_size)
self.linear_h = nn.Linear(input_size, hidden_size)
def forward(self, x, h_0):
# x: (batch_size, seq_len, input_size)
# h_0: (batch_size, 1, hidden_size)
k = self.linear_z(x) # (B, T, H)
log_z = -F.softplus(-k) # log(sigmoid(k))
log_coeffs = -F.softplus(k) # log(1 - sigmoid(k))
# h_0를 log_g로 변환
log_h_0 = log_g(h_0) # (B, 1, H)
# x -> h_tilde -> log_g
log_tilde_h = log_g(self.linear_h(x)) # (B, T, H)
# parallel_scan_log 사용
# b에 해당: log(z) + log(h_tilde)
# a에 해당: log(1 - z) = log_coeffs
# cat([log_h0, log_z + log_tilde_h], dim=1)
return parallel_scan_log(
log_coeffs,
torch.cat([log_h_0, log_z + log_tilde_h], dim=1)
)
# --------------------------------------------------
# 2. minLSTM 클래스 구현
# --------------------------------------------------
class MinLSTM_Sequential(nn.Module):
"""
순차(Sequential) 버전 minLSTM (길이 독립 스케일링 포함)
"""
def __init__(self, input_size, hidden_size):
super().__init__()
self.linear_f = nn.Linear(input_size, hidden_size)
self.linear_i = nn.Linear(input_size, hidden_size)
self.linear_h = nn.Linear(input_size, hidden_size)
def forward(self, x_t, h_prev):
# x_t: (batch_size, 1, input_size)
# h_prev: (batch_size, 1, hidden_size)
f_t = torch.sigmoid(self.linear_f(x_t))
i_t = torch.sigmoid(self.linear_i(x_t))
tilde_h_t = self.linear_h(x_t)
# f', i'로 정규화
f_prime_t = f_t / (f_t + i_t + 1e-12)
i_prime_t = i_t / (f_t + i_t + 1e-12)
h_t = f_prime_t * h_prev + i_prime_t * tilde_h_t
return h_t
class MinLSTM_Parallel(nn.Module):
"""
병렬(Parallel) 버전 minLSTM (Vanilla 버전, 길이 독립 스케일링)
"""
def __init__(self, input_size, hidden_size):
super().__init__()
self.linear_f = nn.Linear(input_size, hidden_size)
self.linear_i = nn.Linear(input_size, hidden_size)
self.linear_h = nn.Linear(input_size, hidden_size)
def forward(self, x, h_0):
# x: (batch_size, seq_len, input_size)
# h_0: (batch_size, 1, hidden_size)
f = torch.sigmoid(self.linear_f(x)) # (B, T, H)
i = torch.sigmoid(self.linear_i(x)) # (B, T, H)
tilde_h = self.linear_h(x) # (B, T, H)
# 길이 독립 스케일링: f' + i' = 1
f_prime = f / (f + i + 1e-12)
i_prime = i / (f + i + 1e-12)
# 병렬 스캔
# coeff = f'
# b = cat([h0, i'*tilde_h], dim=1)
coeff = f_prime
b = torch.cat([h_0, i_prime * tilde_h], dim=1)
return parallel_scan(coeff, b)
class MinLSTM_ParallelLog(nn.Module):
"""
병렬(Parallel) 버전 minLSTM (Log-space 버전, 길이 독립 스케일링)
"""
def __init__(self, input_size, hidden_size):
super().__init__()
self.linear_f = nn.Linear(input_size, hidden_size)
self.linear_i = nn.Linear(input_size, hidden_size)
self.linear_h = nn.Linear(input_size, hidden_size)
def forward(self, x, h_0):
# x: (batch_size, seq_len, input_size)
# h_0: (batch_size, 1, hidden_size)
# diff = log(f') - log(i')를 유도하기 위한 간단한 예시
# 실제론 softplus(-self.linear_f(x)) 등으로 log(sigmoid())를 구해,
# 그 차이를 이용해 f', i'를 구해야 함. (부록 B.2.2 참고)
diff = F.softplus(-self.linear_f(x)) - F.softplus(-self.linear_i(x))
# log_f' = -softplus(diff)
log_f_prime = -F.softplus(diff)
# log_i' = -softplus(-diff)
log_i_prime = -F.softplus(-diff)
log_h_0 = torch.log(h_0 + 1e-12)
log_tilde_h = log_g(self.linear_h(x)) # tilde h에 대한 log
# parallel_scan_log
# a = log_f_prime
# b = log_i_prime + log_tilde_h
return parallel_scan_log(
log_f_prime,
torch.cat([log_h_0, log_i_prime + log_tilde_h], dim=1)
)
# --------------------------------------------------
# 예시 사용
# --------------------------------------------------
if __name__ == "__main__":
# 간단 테스트
batch_size = 2
seq_len = 5
input_size = 3
hidden_size = 4
# 임의 데이터
x_seq = torch.randn(batch_size, seq_len, input_size)
h0 = torch.randn(batch_size, 1, hidden_size)
# minGRU (병렬 버전) 테스트
model_gru_parallel = MinGRU_Parallel(input_size, hidden_size)
out_gru = model_gru_parallel(x_seq, h0)
print("[minGRU Parallel] out shape:", out_gru.shape) # (B, T, H)
# minLSTM (병렬 버전) 테스트
model_lstm_parallel = MinLSTM_Parallel(input_size, hidden_size)
out_lstm = model_lstm_parallel(x_seq, h0)
print("[minLSTM Parallel] out shape:", out_lstm.shape) # (B, T, H)
C.1 데이터셋
Selective Copying
이 과제에서는 모델이 시퀀스 내의 데이터 토큰을 추출하고, 그 외 노이즈 토큰을 무시하도록 학습합니다. Gu & Dao(2024)를 따르며, 어휘(vocabulary) 크기는 16, 시퀀스 길이는 4096입니다. 각 시퀀스에는 무작위 위치에 16개의 데이터 토큰이 들어 있고, 나머지는 노이즈로 채워집니다.
Chomsky Hierarchy
이 과제에서는 Deletang et al.(2023)의 Chomsky 계층(Chomsky Hierarchy) 벤치마크를 사용합니다. 이는 서로 다른 형식 언어(formal language) 작업을 포함하여, 촘스키 계층의 여러 레벨을 아우르는 과제들로 구성됩니다. 또한 Beck et al.(2024)에서 추가로 제안된 Majority, Majority Count 작업도 함께 포함합니다. 모델은 길이가 최대 40인 시퀀스에 대해 학습하며, 일반화(generalization) 능력을 평가하기 위해 길이가 40~256 범위인 시퀀스가 주어졌을 때의 성능을 살펴봅니다.
Long Range Arena
Long Range Arena 벤치마크에서는 시퀀스 길이가 1024부터 4000까지인 세 가지 시퀀스 모델링 과제를 다룹니다. 이는 장기(long-range) 의존성을 평가하기에 적합하도록 설계되었습니다.
- Retrieval: ACL Anthology Network(Radev et al., 2009)에 기반한 과제입니다. 정수 토큰 시퀀스로 표현된 두 개의 인용(citation)이 동일한지 여부를 분류해야 하며, 시퀀스 길이는 4000이고 클래스는 2개입니다.
- ListOps: ListOps(Nangia & Bowman, 2018)의 확장 버전입니다. 전위 표기(prefix notation)의 중첩된 수식(nested mathematical expression)을 계산하여 결과를 도출하는 과제이며, 시퀀스 길이는 2048, 클래스는 10개입니다.
- G-Image: CIFAR-10(Krizhevsky, 2009)에 기반하여, 32×32 크기의 이미지를 그레이스케일로 변환한 뒤 해당 이미지의 클래스를 예측하는 과제입니다. 시퀀스 길이는 1024이고 클래스는 10개입니다.
강화학습
이 설정에서는 D4RL(Fu et al., 2020) 벤치마크에 속한 MuJoCo 연속 제어 과제를 사용합니다. HalfCheetah, Hopper, Walker 세 가지 환경을 대상으로 하며, 보상 함수가 조밀(dense)하게 주어집니다. 각 환경마다 데이터 품질이 서로 다른 세 가지 데이터셋을 사용합니다.
- Medium (M): 전문가 정책(expert policy) 점수의 약 1/3 수준으로 학습된 정책이 100만 스텝을 샘플링한 데이터셋
- Medium-Replay (M-R): Medium 수준 정책을 학습하는 과정에서 생성된 리플레이 버퍼(replay buffer)를 수집한 데이터셋
- Medium-Expert (M-E): Medium 수준 정책이 100만 스텝, 전문가 정책이 100만 스텝을 수행해 합쳐진 총 200만 스텝 데이터셋
Fu et al.(2020)의 설정에 따라, 전문가 정책을 100점으로 정규화하여 점수를 보고합니다.
언어 모델링
이 설정에서는 Shakespeare 데이터셋을 사용합니다. 윌리엄 셰익스피어(William Shakespeare)의 작품에서 추출된 텍스트 자료로 구성되며, 학습용 텍스트는 약 1,003,854개 토큰, 테스트용 텍스트는 약 111,540개 토큰으로 이루어져 있습니다.
C.2 아키텍처(Architecture)
본 연구의 주된 목표는 minLSTM, minGRU처럼 간소화된 RNN 구조가 최신 시퀀스 모델과 견줄 만한 성능을 낼 수 있음을 보이는 것입니다. 이를 위해, 우리는 잔차 연결(residual connection), 정규화(normalization), RNN의 확장된 은닉 상태를 위한 다운프로젝션(downprojection) 레이어 등 일반적으로 쓰이는 최소한의 구성만을 사용했습니다. 언어 모델링이나 Long Range Arena처럼 복잡한 과제에는 (합성곱 레이어와 MLP 같은) 표준 구성요소를 추가로 활용했습니다.^4
- Selective Copying: 추가 구성요소 없음.
- Chomsky Hierarchy: Conv4→minRNN. 즉, 커널 크기가 4인 합성곱 레이어를 시간축 방향으로 적용한 뒤 최소형 RNN을 사용.
- Long Range Arena: Conv4→minRNN→
- Language Modelling: Conv4→minRNN
- Reinforcement Learning: minRNN→

C.3 하이퍼파라미터 및 일반적 실험 세부사항
- Selective Copying
- Gu & Dao(2024)의 설정을 따릅니다.
- 총 40만 스텝 학습, 배치 크기 64, 입력 차원 64.
- GPU 메모리 제한으로, 배치 크기 32인 두 미니배치를 그래디언트 누적 후 한 번의 업데이트를 수행(Gradient Accumulation)했으며, 기울기는 1.0으로 클리핑.
- 옵티마이저는 Adam, 학습률 10^-4, 얼리 스토핑(early stopping) 사용.
- 모델은 3레이어, 드롭아웃 0.1. minLSTM과 minGRU는 확장 팩터(expansion factor) 6을 사용.
- 베이스라인 결과는 Mamba 논문에서 인용.
- Long Range Arena
- Beck et al.(2024)의 설정을 참고했습니다.
- Retrieval: 레이어(블록) 6개, 임베딩 차원 128, 배치 크기 64로 학습.
- ListOps: 레이어(블록) 8개, 임베딩 차원 128, 배치 크기 32로 학습.
- G-Image: 레이어(블록) 6개, 임베딩 차원 512, 배치 크기 64로 학습.
- 전부 25만 스텝 동안 학습, 옵티마이저는 AdamW(학습률 0.001, weight decay 0.05), 전체 스텝의 10%를 선형 웜업(linear warm-up) 후 코사인 감소(cosine annealing).
- Chomsky Hierarchy
- Beck et al.(2024)의 설정을 따라 2블록 구성 모델을 사용.
- 50만 스텝 동안 학습, 배치 크기 256, 옵티마이저는 AdamW(학습률 3×10^-4, weight decay 0.01).
- Language Modelling
- 옵티마이저는 AdamW(학습률 1×10&-3).
- 레이어는 3개, 드롭아웃 0.2, 임베딩 차원 384, 총 5천 스텝을 배치 크기 64로 학습. 25스텝마다 성능 평가.
- 기울기는 0.25로 클리핑.
- Transformer의 헤드는 6개. Mamba는 SSM 확장 팩터 16, 블록 확장 팩터 2 사용. minLSTM, minGRU는 Mamba를 따라 확장 팩터 2 사용.
- Reinforcement Learning
- Ota(2024)의 하이퍼파라미터 설정을 따릅니다.
- Hopper(Medium)와 Hopper(Medium-Replay)는 임베딩 차원 256, 나머지 환경들은 임베딩 차원 128 사용.
- Hopper(Medium), Hopper(Medium-Replay), Walker(Medium)는 학습률 , 그 외는 10^-3.
- 옵티마이저는 AdamW(weight decay 1×10−41 \times 10^{-4}), 1만 스텝 선형 웜업.
- 모델은 3레이어, 드롭아웃 0.1. 10만 스텝을 배치 크기 64로 학습.
- 베이스라인 결과는 Mamba와 Aaren 논문에서 인용했습니다.
D.1 Chomsky Hierarchy & Long Range Arena
본 절에서는 Chomsky Hierarchy(Deletang et al., 2023)와 Long Range Arena(Tay et al., 2021) 벤치마크 실험을 진행합니다. 이 두 벤치마크는 시퀀스 모델의 일반화(generalization) 능력과 장기(long-range) 의존성 처리 능력을 평가하기 위해 널리 활용되며, 현대 시퀀스 모델링 과제에 매우 중요한 요소들을 다루고 있습니다.
우리는 Minimal RNNs(minLSTM, minGRU 등)과 완전 병렬화가 가능한 다른 모델들—예: RWKV, Mamba, xLSTM[1:0](병렬화된 mLSTM 모듈 사용)—을 비교했습니다. Beck et al.(2024)의 설정을 따라, Chomsky Hierarchy 과제 중에서 모델이 최소 30% 이상의 정확도를 달성(부분적으로나마 해결 가능함을 의미)한 작업들에 집중했습니다. 하이퍼파라미터는 xLSTM 논문과 동일하게 설정하였고, 결과 신뢰도를 높이기 위해 3개 시드(Seed)에 대해 평균을 냈습니다. 베이스라인 결과(정확도, 높을수록 좋음)는 xLSTM 논문의 그림 4(Chomsky Hierarchy)와 표 6(Long Range Arena)에서 인용했습니다.
표 4와 확장판인 표 5에서 확인할 수 있듯, Minimal RNN들은 이 두 벤치마크 전 과제에서 최첨단(SoTA) 모델(Mamba, xLSTM 등)에 견줄 만한, 매우 경쟁력 있는 성능을 보여주었습니다. 특히 Retention, Hyena, RWKV, Llama와 같은 다른 모델들을 능가하는 결과를 얻어, 간소화된 전통 RNN 모델의 잠재력을 다시금 입증했습니다.
D.2 추론(Inference) 런타임 비교
본 실험에서는 GRU, LSTM, minGRU, minLSTM, 그리고 Mamba(공식 구현 사용)의 추론 속도를 비교했습니다. 이때 사용한 하드웨어 및 구현 방식에 따라 결과가 달라질 수 있음을 유의해야 합니다.
실험 설정
- 배치 크기(batch size): 8, 16, 32, 64
- 시퀀스 길이(sequence length): 최대 2048까지
- 각 조건에서 50회 반복 실행하여 평균 추론 속도 측정
- 추론 전 맥락(context) 토큰도 고려하여 시간 측정
결과 분석
그림 3에 나타난 결과에 따르면, 맥락 토큰을 순차적으로 처리해야 하는 GRU와 LSTM은 병렬 처리가 가능한 minGRU, minLSTM, Mamba보다 추론 시간이 훨씬 깁니다.
- minLSTM, minGRU vs. Mamba
- 배치 크기 8, 16, 32, 64 각각에 대해 측정했을 때, minGRU는 Mamba보다 각각 6.6%, 4.1%, 4.9%, 2.9% 더 빨랐습니다.
- minLSTM는 같은 배치 크기에서 Mamba보다 각각 3.6%, 2.9%, 0%, 1.3% 더 느리거나 비슷한 수준을 보였습니다.
따라서 minLSTM과 minGRU는 LSTM과 GRU를 단순화한 구조이므로, 이론적으로나 실제 실험에서나 추론 시 더 빠른 동작을 기대할 수 있습니다. 그림 4에서 보이듯, 시퀀스 길이와 배치 크기가 변하더라도 minGRU와 minLSTM은 GRU, LSTM보다 훨씬 효율적인 추론 속도를 보여 주는데, 배치 크기가 64일 때 minGRU는 GRU보다 19.6% 빠르고, minLSTM은 LSTM보다 41.5%나 빠른 성능을 보였습니다.
D.3 아키텍처 소거(Ablation) 실험
본 연구의 주요 목표는 minLSTM과 minGRU 같은 간소화된 RNN 구조가 현대의 최첨단(SoTA) 시퀀스 모델과 견줄 만한 성능을 낼 수 있음을 입증하는 것입니다. 이를 위해, 우리는 잔차 연결(residual connection), 정규화(normalization), RNN에서 확장된 은닉 상태를 위한 다운프로젝션(downprojection) 레이어 등 기본적인 설계 방식만을 적용한 최소주의(minimalistic) 아키텍처를 채택했습니다. 또한, 언어 모델링이나 Long Range Arena처럼 복잡한 과제에서는 합성곱 레이어와 MLP를 추가로 도입했습니다.
이러한 아키텍처 선택이 모델 성능에 미치는 영향을 더 구체적으로 파악하기 위해, Long Range Arena의 ListOps 데이터셋을 대상으로 추가 구성요소에 대한 소거(ablation) 실험을 수행했습니다. 표 6은 3개 시드(Seed)에 대한 평균 결과를 제시하고 있으며, minLSTM 모델에 여러 레이어를 추가했을 때 성능이 어떻게 달라지는지를 보여 줍니다. ListOps의 경우, 합성곱 레이어(Conv)와 MLP를 도입했을 때 성능이 향상되는 경향을 확인할 수 있었습니다.
D.4 초기화(Initialization) 분석
이번 실험에서는 모델 성능에 미치는 초기화 방식의 영향을 살펴봅니다. 작업 유형에 따라, 모델이 시간을 두고 정보를 계속 유지하도록 유도하는 것이 유리할 수 있습니다. 이를 달성하는 한 가지 방법은 minLSTM의 망각 게이트(forget gate) 바이어스를 높이는 것으로, 학습 초기부터 정보 유지 성향을 강화하는 효과가 있습니다. 이처럼 망각 게이트 바이어스를 증가시키면, LSTM의 망각 게이트 f_는 f_t에 가까워집니다. 그림 5에 나타나 있듯, 망각 게이트 바이어스를 높인 minLSTM은 학습 효율이 개선되어, 더 빠른 수렴 속도와 안정적인 학습 과정을 보여 줍니다.

표 4: Chomsky Hierarchy와 Long Range Arena 벤치마크 결과. 여기서 우리는 완전 병렬화가 가능한 모델인 RWKV, Mamba, xLSTM[1:0](mLSTM 모듈 사용) 등과 minLSTM을 비교했습니다. (정확도: 높을수록 좋음) 베이스라인 결과는 xLSTM 논문의 그림 4(Chomsky Hierarchy)와 표 6(Long Range Arena)에서 인용했습니다. 결과적으로, minLSTM은 Mamba, xLSTM 등 최신 모델과 견줄 만한 성능을 보였으며, 해당 벤치마크의 모든 작업에서 경쟁력 있는 성과를 달성했습니다.
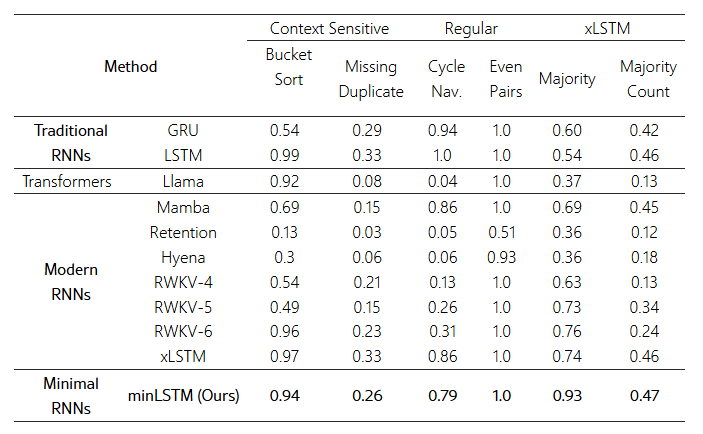
표 5: Chomsky Hierarchy 벤치마크에 대한 확장 결과. (정확도: 높을수록 좋음) 베이스라인 결과는 xLSTM 논문의 그림 4에서 가져왔습니다. RWKV, Mamba, xLSTM[1:0](mLSTM 모듈 사용) 등 완전 병렬화 모델과 minLSTM을 비교한 결과, minLSTM은 Mamba, xLSTM 등 최신 모델과 견줄 만한 성능을 거두었을 뿐 아니라, Retention, Hyena, RWKV, Llama 등 다른 모델들보다도 우수한 성능을 보였습니다.
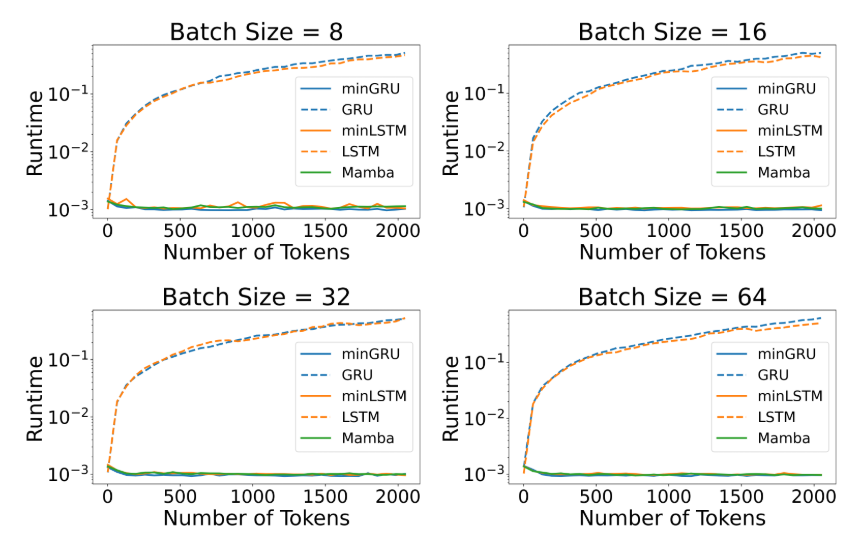
그림 3: 맥락(context) 토큰을 고려한 추론 런타임 비교: 병렬화 가능한 RNN(minLSTM, minGRU, Mamba) vs. 전통적 RNN(LSTM, GRU). 시퀀스 모델이 처리해야 하는 맥락 토큰이 늘어날수록, 순차 계산 방식의 LSTM과 GRU는 병렬화가 가능한 minLSTM, minGRU, Mamba보다 훨씬 느린 추론 시간을 보입니다.

그림 4: 추론 런타임 비교: 최소형 RNN(minLSTM, minGRU) vs. 전통 RNN(LSTM, GRU). LSTM과 GRU를 간소화한 minLSTM과 minGRU는 대체로 더 빠른 추론 시간을 나타내는데, 특히 배치 크기가 클수록 그 차이가 크게 드러납니다.
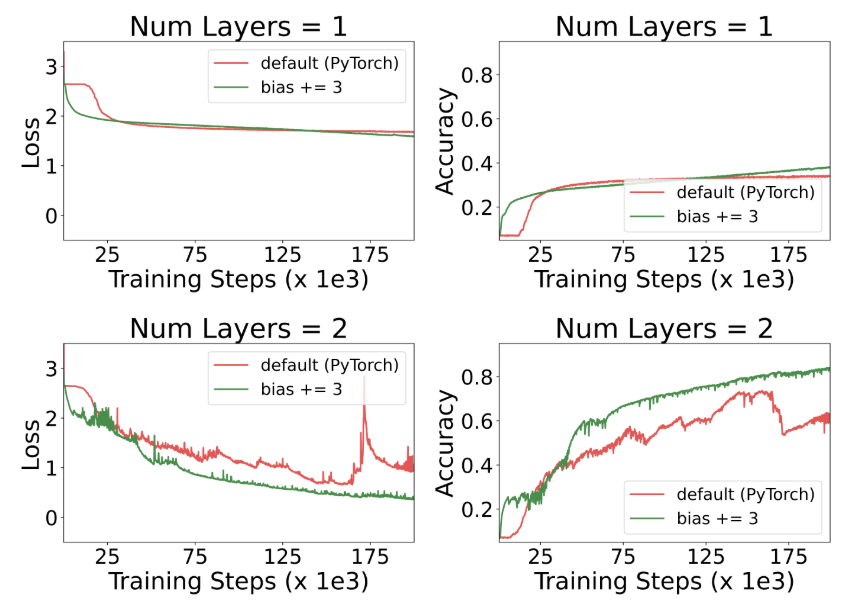
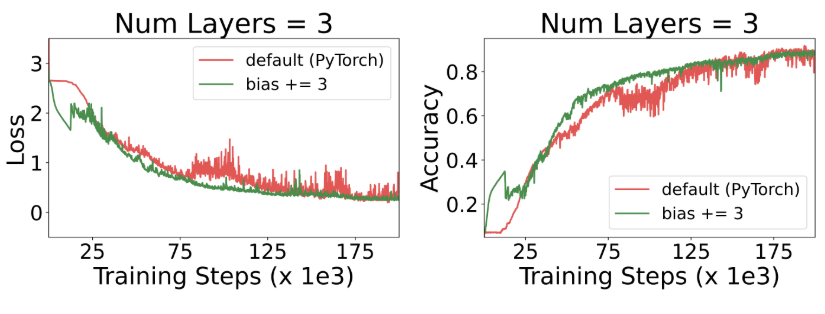
그림 5: 망각 게이트 바이어스 초기화가 학습 효율에 미치는 영향. 망각 게이트 바이어스를 높인 minLSTM은 초반부터 정보가 사라지는 것을 방지하여 학습 속도를 높이고, 전반적으로 더 안정적인 학습 과정을 보여 줍니다.

표 6: Long Range Arena의 ListOps 과제에서 아키텍처 소거(Ablation) 실험. (정확도: 높을수록 좋음, 3개 시드 평균) 언어 모델링과 Long Range Arena처럼 복잡한 과제에서는 합성곱 레이어(Conv)와 MLP를 추가로 도입했을 때 성능이 향상되는 경향을 확인할 수 있었습니다.
Parallel Scan
minLSTM과 minGRU를 포함하여, 최근 제안된 여러 시퀀스 모델들은 모두 병렬 스캔(Parallel Scan) 알고리즘을 사용해 학습 가능한 함수 계열의 일종으로 볼 수 있습니다. 즉,

본 연구에서는 minLSTM과 minGRU를 순수 PyTorch로 구현했습니다. 하지만 병렬 스캔을 활용하는 여러 모델들은 재귀 구조가 유사하기 때문에, 한 모델에서 적용한 트레이닝 속도 향상 기법(예: 청킹(chunking))을 다른 모델(예: minGRU, minLSTM)에도 그대로 응용할 수 있습니다.
매개변수 초기화(Parameter Initializations)
최근 제안된 순환 시퀀스 모델을 시간에 따라 펼쳐서(unroll) 계산하면, 출력이나 기울기가 소실·폭발하는 현상이 자주 관찰됩니다(Wang et al., 2024b). 이는 출력 스케일이 시간 의존적(time-dependent)이기 때문인데, 이 때문에 여러 상태공간 모델(Gu et al., 2020, 2022; Orvieto et al., 2023)에서는 모델 안정성을 위해 특정 분포에 따라 매개변수를 초기화하도록 권장합니다.
반면 minLSTM과 minGRU는 기본 PyTorch 초기화만으로도 이미 충분히 안정적으로 학습되는 모습을 보였습니다. 이는 상태공간 모델(SSM)과 달리, minLSTM과 minGRU의 출력 스케일이 시간에 대해 독립적(time-independent)이라 잠재적 불안정 요소를 피할 수 있기 때문입니다.