https://arxiv.org/abs/1607.06450
Layer Normalization
Training state-of-the-art, deep neural networks is computationally expensive. One way to reduce the training time is to normalize the activities of the neurons. A recently introduced technique called batch normalization uses the distribution of the summed
arxiv.org
초록
최신의 심층 신경망을 훈련시키는 것은 계산 비용이 많이 듭니다. 훈련 시간을 단축하는 한 가지 방법은 뉴런의 활동을 정규화하는 것입니다. 최근에 도입된 기법인 배치 정규화(batch normalization)는 훈련 사례의 미니 배치에서 뉴런에 들어오는 입력의 총합 분포를 이용하여 평균과 분산을 계산하고, 이를 각 훈련 사례에서 해당 뉴런에 대한 총합 입력을 정규화하는 데 사용합니다. 이 방법은 피드포워드 신경망의 훈련 시간을 크게 단축시킵니다. 그러나 배치 정규화의 효과는 미니 배치 크기에 의존하며, 이를 순환 신경망(recurrent neural networks, RNN)에 적용하는 방법은 명확하지 않습니다. 본 논문에서는 배치 정규화를 레이어 정규화(layer normalization)로 전환하여, 단일 훈련 사례에서 한 계층 내의 모든 뉴런에 대한 총합 입력으로부터 정규화에 필요한 평균과 분산을 계산합니다. 배치 정규화와 마찬가지로, 정규화 후 비선형 활성화 함수가 적용되기 전에 각 뉴런에 대해 적응형 바이어스와 게인을 부여합니다. 다만, 배치 정규화와 달리 레이어 정규화는 훈련 시와 테스트 시에 동일한 계산을 수행합니다. 또한, 각 시간 단계마다 정규화 통계를 별도로 계산함으로써 순환 신경망에 간단하게 적용할 수 있습니다. 레이어 정규화는 순환 신경망의 은닉 상태 동역학을 안정화하는 데 매우 효과적이며, 실험 결과 기존 기법에 비해 훈련 시간을 크게 단축할 수 있음을 보여줍니다.
1. 서론
확률적 경사 하강법(Stochastic Gradient Descent)의 여러 변형으로 훈련된 심층 신경망은 컴퓨터 비전 [Krizhevsky et al., 2012] 및 음성 처리 [Hinton et al., 2012]와 같은 다양한 감독 학습 과제에서 기존 방법들을 상당히 능가하는 성능을 보였습니다. 그러나 최신 심층 신경망은 종종 수일간의 훈련을 필요로 합니다. 학습 속도를 높이기 위해 서로 다른 머신에서 훈련 사례의 하위 집합에 대해 기울기를 계산하거나, 신경망 자체를 여러 머신에 분산시키는 방법이 가능하지만 [Dean et al., 2012], 이는 많은 통신과 복잡한 소프트웨어를 요구하며, 병렬화 정도가 증가할수록 수익이 급격히 감소하는 경향이 있습니다. 또 다른 접근법은 신경망의 순전파 과정에서 수행되는 계산을 수정하여 학습을 용이하게 만드는 것입니다. 최근 배치 정규화 [Ioffe and Szegedy, 2015]가 심층 신경망에 추가적인 정규화 단계를 포함시킴으로써 훈련 시간을 단축하는 방법으로 제안되었습니다. 이 정규화 기법은 훈련 데이터 전체에서 각 총합 입력을 해당 평균과 표준 편차를 사용해 표준화합니다. 배치 정규화를 적용한 피드포워드 신경망은 단순한 SGD를 사용하더라도 더 빠르게 수렴합니다. 훈련 시간 단축 외에도, 배치 통계로 인한 확률적 특성이 훈련 과정에서 정규화 효과를 제공합니다.
비록 단순하지만, 배치 정규화는 총합 입력 통계의 이동 평균을 필요로 합니다. 고정 깊이의 피드포워드 신경망에서는 각 은닉층마다 통계를 별도로 저장하는 것이 간단합니다. 그러나 순환 신경망(RNN)의 순환 뉴런에 대한 총합 입력은 시퀀스 길이에 따라 달라지기 때문에, RNN에 배치 정규화를 적용하려면 시간 단계마다 서로 다른 통계가 필요한 것으로 보입니다. 게다가, 배치 정규화는 온라인 학습 과제나 미니 배치 크기가 작아야 하는 매우 큰 분산 모델에는 적용하기 어렵습니다.
본 논문은 다양한 신경망 모델의 훈련 속도를 개선하기 위한 간단한 정규화 기법인 레이어 정규화를 소개합니다. 배치 정규화와 달리, 제안하는 방법은 은닉층 내의 뉴런에 대한 총합 입력으로부터 직접 정규화 통계를 추정하여, 정규화가 훈련 사례 간에 새로운 종속성을 도입하지 않도록 합니다. 우리는 레이어 정규화가 RNN에 효과적으로 작동하며, 여러 기존 RNN 모델의 훈련 시간과 일반화 성능을 모두 개선함을 보입니다.
2. 배경
피드포워드 신경망은 입력 패턴 𝕩를 출력 벡터 y로 매핑하는 비선형 함수입니다. 심층 피드포워드 신경망의 l번째 은닉층을 고려하고, 해당 층의 뉴런들에 대한 합산 입력을 나타내는 벡터를 aₗ 라고 합시다. 합산 입력은 가중치 행렬 Wₗ 과 하위 계층에서 전달받은 입력 hₗ 을 이용한 선형 변환을 통해 계산되며, 다음과 같이 주어집니다:
aᵢₗ = (wᵢₗ)ᵀ hₗ
hᵢₗ₊₁ = f(aᵢₗ + bᵢₗ) (1)
여기서 f(⋅)는 원소별로 적용되는 비선형 함수이며, wᵢₗ은 i번째 은닉 유닛에 들어오는 가중치 벡터, bᵢₗ은 스칼라 바이어스 파라미터입니다. 신경망의 파라미터는 역전파를 통해 계산된 기울기를 사용한 기울기 기반 최적화 알고리즘으로 학습됩니다.
딥러닝의 도전 과제 중 하나는 한 층의 가중치에 대한 기울기가 이전 층의 뉴런 출력에 크게 의존한다는 점입니다. 특히, 이전 층의 출력들이 높은 상관관계로 변화할 경우 그 의존성이 더욱 두드러집니다. 이러한 바람직하지 않은 “공변량 이동(covariate shift)”을 줄이기 위해 배치 정규화 [Ioffe and Szegedy, 2015]가 제안되었습니다. 이 기법은 훈련 사례 전체에 걸쳐 각 은닉 유닛의 합산 입력을 정규화합니다. 구체적으로, l번째 층의 i번째 합산 입력에 대해 배치 정규화 기법은 데이터 분포 하에서의 분산에 따라 합산 입력을 재조정합니다.
āᵢₗ = (gᵢₗ / σᵢₗ) (aᵢₗ − μᵢₗ)
μᵢₗ = 𝔼₍𝕩∼P(𝕩)₎[aᵢₗ]
σᵢₗ = 𝔼₍𝕩∼P(𝕩)₎[(aᵢₗ − μᵢₗ)²] (2)
여기서 āᵢₗ는 l번째 층의 i번째 은닉 유닛에 대해 정규화된 합산 입력이며, gᵢₗ은 비선형 활성화 함수가 적용되기 전에 정규화된 활성화를 스케일링하는 게인 파라미터입니다. 이때 기대값은 전체 훈련 데이터 분포에 대해 계산됨을 주의해야 합니다. 식 (2)의 기대값을 정확하게 계산하기 위해서는 현재의 가중치 집합을 사용하여 전체 훈련 데이터를 순전파해야 하므로, 이는 일반적으로 실용적이지 않습니다. 대신 μ와 σ는 현재 미니 배치로부터 얻은 경험적 샘플들을 사용하여 추정됩니다. 이로 인해 미니 배치의 크기에 제약이 생기며, 순환 신경망에 적용하기 어렵게 됩니다.
3. 레이어 정규화
이제 배치 정규화의 단점을 극복하기 위해 고안된 레이어 정규화 방법을 살펴보겠습니다.
한 층의 출력이 변화하면, 특히 출력이 크게 달라질 수 있는 ReLU 유닛의 경우, 다음 층의 합산 입력에도 높은 상관 관계를 가지는 변화가 발생하게 됩니다. 이는 각 층 내에서 합산 입력의 평균과 분산을 고정함으로써 “공변량 이동(covariate shift)” 문제를 줄일 수 있음을 시사합니다. 따라서, 동일한 층의 모든 은닉 유닛에 대해 레이어 정규화 통계를 다음과 같이 계산합니다:
μₗ = (1/H) ∑₍ᵢ₌₁₎ᴴ aᵢₗ
σₗ = (1/H) ∑₍ᵢ₌₁₎ᴴ (aᵢₗ − μₗ)² (3)
여기서 H는 한 층에 있는 은닉 유닛의 수를 의미합니다.
식 (2)와 식 (3)의 차이는, 레이어 정규화에서는 동일한 층 내의 모든 은닉 유닛이 동일한 정규화 항(μ와 σ)을 공유하지만, 서로 다른 훈련 사례들은 각기 다른 정규화 항을 가진다는 점입니다. 배치 정규화와 달리, 레이어 정규화는 미니 배치 크기에 어떠한 제약도 두지 않으며, 배치 크기가 1인 순수 온라인 환경에서도 사용할 수 있습니다.
3.1 레이어 정규화된 순환 신경망
최근의 시퀀스 투 시퀀스 모델 [Sutskever et al., 2014]은 자연어 처리에서 순차 예측 문제를 해결하기 위해 소형 순환 신경망(RNN)을 활용합니다. NLP 작업에서는 훈련 사례마다 문장 길이가 다를 수 있는데, 이는 모든 시간 단계에서 동일한 가중치가 사용되는 RNN에서는 쉽게 다룰 수 있습니다. 그러나 배치 정규화를 RNN에 명백한 방식으로 적용하면, 시퀀스의 각 시간 단계마다 별도의 통계를 계산하고 저장해야 하므로, 테스트 시퀀스가 훈련 시퀀스보다 길 경우 문제가 발생할 수 있습니다. 레이어 정규화는 현재 시간 단계의 한 층에 대한 합산 입력만을 고려하기 때문에 이러한 문제가 없으며, 모든 시간 단계에서 공유되는 단일 게인 및 바이어스 파라미터 집합만을 사용합니다.
일반적인 RNN에서는 순환 층의 합산 입력이 현재 입력 𝕩ₜ와 이전 은닉 상태 벡터 hₜ₋₁로부터 아래와 같이 계산됩니다:
aₜ = Wₕʰ · hₜ₋₁ + Wₓʰ · 𝕩ₜ.
레이어 정규화된 순환 층은 식 (3)과 유사한 추가 정규화 항을 사용하여 활성화를 재중심화 및 재스케일링합니다:
hₜ = f[ (g/σₜ) ⊙ (aₜ − μₜ) + b ]
μₜ = (1/H) ∑₍ᵢ₌₁₎ᴴ aᵢₜ
σₜ = (1/H) ∑₍ᵢ₌₁₎ᴴ (aᵢₜ − μₜ)² (4)
여기서 Wₕʰ는 순환 은닉층 간의 가중치, Wₓʰ는 하위 계층에서 은닉층으로 전달되는 가중치를 나타냅니다.
⊙는 두 벡터 간의 원소별 곱셈을 의미하며, b와 g는 hₜ와 동일한 차원의 바이어스와 게인 파라미터로 정의됩니다.
일반적인 RNN에서는 순환 유닛에 대한 합산 입력의 평균 크기가 매 시간 단계마다 증가하거나 감소하는 경향이 있어, 기울기가 폭발하거나 소실되는 문제가 발생합니다. 반면, 레이어 정규화된 RNN은 모든 합산 입력의 스케일을 재조정하더라도 불변성을 유지하는 정규화 항 덕분에 은닉층 간의 동역학이 훨씬 안정적으로 유지됩니다.
4. 관련 연구
배치 정규화는 이전에 순환 신경망에 확장되어 적용된 바 있습니다 [Laurent et al., 2015, Amodei et al., 2015, Cooijmans et al., 2016]. 이전 연구 [Cooijmans et al., 2016]에서는 각 시간 단계마다 독립적인 정규화 통계를 유지하는 것이 순환 배치 정규화의 최상의 성능을 달성하는 방법임을 제시합니다. 저자들은 순환 배치 정규화 층에서 게인 파라미터를 0.1로 초기화하는 것이 모델의 최종 성능에 상당한 차이를 만든다는 것을 보여줍니다. 우리의 연구는 또한 weight normalization [Salimans and Kingma, 2016]과 관련이 있습니다. weight normalization에서는 분산 대신에 들어오는 가중치의 L2 노름을 사용하여 뉴런의 합산 입력을 정규화합니다. 예상 통계를 이용하여 weight normalization이나 batch normalization을 적용하는 것은 원래의 피드포워드 신경망을 다른 방식으로 파라미터화하는 것과 동일합니다. ReLU 네트워크에서의 재파라미터화는 Path-normalized SGD [Neyshabur et al., 2015]에서 연구되었습니다. 그러나, 우리가 제안하는 레이어 정규화 방법은 원래의 신경망을 재파라미터화한 것이 아닙니다. 따라서 레이어 정규화된 모델은 다른 방법들과는 다른 불변성 특성을 가지며, 이는 다음 섹션에서 다룰 예정입니다.
게인 파라미터(일명 γ 파라미터)는 정규화된 활성화값의 크기를 조정하기 위해 학습되는 매개변수입니다.
정규화 과정에서는 각 뉴런의 출력값을 평균 0, 분산 1로 조정하지만, 이렇게 하면 모델이 원래의 표현력을 잃을 수 있습니다. 그래서 게인 파라미터를 곱해줌으로써 네트워크가 필요한 범위와 스케일로 다시 조정할 수 있게 해줍니다.
5. 분석
본 섹션에서는 다양한 정규화 방식의 불변성(invariance) 특성을 조사합니다.
5.1 가중치 및 데이터 변환에 대한 불변성
제안된 레이어 정규화는 배치 정규화 및 weight normalization과 관련이 있습니다. 비록 정규화 스칼라(μ와 σ)를 계산하는 방식은 다르지만, 이들 방법은 뉴런의 합산 입력 aᵢ를 μ와 σ라는 두 스칼라를 통해 정규화한다는 점에서 공통점을 가집니다. 또한, 정규화 후 각 뉴런에 대해 적응형 바이어스 b와 게인 g를 학습합니다.
hᵢ = f( (gᵢ / σᵢ) (aᵢ − μᵢ) + bᵢ ) (5)
참고로, 레이어 정규화와 배치 정규화에서는 μ와 σ가 각각 식 (2)와 식 (3)에 따라 계산됩니다. 반면, weight normalization에서는 μ가 0이고, σ = ‖w‖₂입니다.
아래 표 1은 세 가지 정규화 방법에 대한 불변성 결과를 요약한 것입니다.
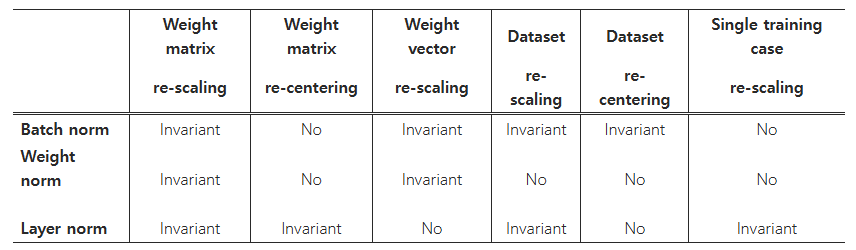
표 1: 정규화 방법에 따른 불변성 속성
가중치 재스케일링 및 재중심화:
우선, 배치 정규화와 weight normalization에서는 한 뉴런에 들어오는 가중치 wᵢ의 임의의 재스케일링이 그 뉴런의 정규화된 합산 입력에 아무런 영향을 미치지 않음을 관찰할 수 있습니다. 구체적으로, 배치 정규화와 weight normalization 하에서 가중치 벡터가 δ로 스케일링되면, 두 스칼라인 μ와 σ 역시 δ로 스케일링되어 정규화된 합산 입력은 스케일링 전후에 동일하게 유지됩니다. 즉, 이 두 정규화 방식은 가중치의 재스케일링에 대해 불변입니다.
반면, 레이어 정규화는 개별 가중치 벡터의 재스케일링에는 불변이 아닙니다. 대신, 레이어 정규화는 전체 가중치 행렬의 스케일링과, 가중치 행렬 내 모든 들어오는 가중치에 대한 이동(shift)에 대해 불변입니다.
예를 들어, 두 모델 파라미터 집합 θ와 θ′가 존재하고, 이들의 가중치 행렬 W와 W′가 스케일링 계수 δ에 의해 다르며, W′의 모든 들어오는 가중치가 상수 벡터 𝜸에 의해 이동된 경우, 즉
W′ = δW + 1𝜸ᵀ
라고 할 때, 레이어 정규화 하에서는 두 모델이 사실상 동일한 출력을 계산합니다:
h′ = f( (g / σ′) ⊙ (W′x − μ′) + b )
= f( (g / σ′) ⊙ ((δW + 1𝜸ᵀ)x − μ′) + b )
= f( (g / σ) ⊙ (Wx − μ) + b )
= h (6)
여기서 ⊙는 원소별 곱셈을 의미합니다.
또한, 만약 정규화가 가중치 이전의 입력에만 적용된다면, 모델은 가중치의 재스케일링 및 재중심화에 대해 불변하지 않게 됩니다.
데이터 재스케일링 및 재중심화:
모든 정규화 기법은 데이터셋의 재스케일링에 대해 불변임을, 뉴런의 합산 입력이 이러한 변화 하에서도 일정하게 유지됨을 통해 확인할 수 있습니다.
더욱이, 레이어 정규화는 각 훈련 사례에 대해 재스케일링이 이루어져도 불변입니다. 이는 식 (3)에서의 정규화 스칼라인 μ와 σ가 현재 입력 데이터에만 의존하기 때문입니다.
예를 들어, 𝕩를 δ로 재스케일링하여 얻은 새로운 데이터 포인트 𝕩′가 있다고 하면,
hᵢ′ = f( (gᵢ / σᵢ′) (wᵢᵀ 𝕩′ − μ′) + bᵢ )
= f( (gᵢδ / σ) (δwᵢᵀ 𝕩 − δμ) + bᵢ )
= hᵢ (7)
즉, 개별 데이터 포인트의 재스케일링은 레이어 정규화 하에서 모델의 예측을 변경하지 않습니다.
레이어 정규화에서 가중치 행렬의 재중심화와 유사하게, 배치 정규화 또한 데이터셋의 재중심화에 대해 불변임을 보일 수 있습니다.

- Layer Normalization의 불변성:
예를 들어 보겠습니다. 어떤 레이어의 입력값이 [2, 4, 6]이라고 해보죠.
# 원래 입력
inputs = [2, 4, 6]
mean = (2 + 4 + 6) / 3 = 4
std = sqrt(((2-4)² + (4-4)² + (6-4)²) / 3) = 1.63
normalized = [(2-4)/1.63, (4-4)/1.63, (6-4)/1.63]
= [-1.22, 0, 1.22]
# 입력을 2배로 스케일링
scaled_inputs = [4, 8, 12]
new_mean = (4 + 8 + 12) / 3 = 8
new_std = sqrt(((4-8)² + (8-8)² + (12-8)²) / 3) = 3.26
new_normalized = [(4-8)/3.26, (8-8)/3.26, (12-8)/3.26]
= [-1.22, 0, 1.22] # 결과가 같음!이처럼 입력 전체를 스케일링해도 정규화 후의 값은 동일하게 됩니다.
- Batch Normalization의 불변성:
배치 정규화에서 가중치를 스케일링하는 경우를 보겠습니다:
# 원래 계산
weight = 2
inputs = [1, 2, 3]
outputs = [2*1, 2*2, 2*3] = [2, 4, 6]
mean = 4
std = 1.63
normalized = [-1.22, 0, 1.22]
# 가중치를 2배로 스케일링
new_weight = 4
new_outputs = [4*1, 4*2, 4*3] = [4, 8, 12]
new_mean = 8
new_std = 3.26
new_normalized = [-1.22, 0, 1.22] # 결과가 같음!- Weight Normalization의 불변성:
가중치 정규화에서는 가중치 벡터의 크기로 나누기 때문에 스케일링에 불변합니다:
# 원래 가중치
w = [3, 4] # L2 norm = 5
normalized_w = [3/5, 4/5]
# 가중치를 2배로 스케일링
w_scaled = [6, 8] # L2 norm = 10
normalized_w_scaled = [6/10, 8/10] = [3/5, 4/5] # 결과가 같음!
불변하지 않는 경우의 예:
# Weight Normalization에서 데이터 스케일링
w = [3, 4] # normalized = [0.6, 0.8]
x = [1, 1]
output = 0.6*1 + 0.8*1 = 1.4
# 데이터를 2배로 스케일링
x_scaled = [2, 2]
new_output = 0.6*2 + 0.8*2 = 2.8 # ≠ 1.4이렇게 각 정규화 방법은 특정 변환에 대해서는 출력이 변하지 않고(불변), 다른 변환에 대해서는 출력이 변하게 됩니다. 이러한 성질은 각 정규화 방법의 수학적 정의에서 자연스럽게 도출되며, 이는 각 방법의 장단점이 되기도 합니다.
5.2 학습 중 파라미터 공간의 기하학
모델의 예측이 파라미터의 재중심화 및 재스케일링에 대해 불변임을 조사했습니다. 그러나 모델들이 동일한 근본 함수를 표현함에도 불구하고, 서로 다른 파라미터화 방식에서는 학습의 동작 방식이 매우 달라질 수 있습니다. 본 섹션에서는 파라미터 공간의 기하학과 다양체(manifold)를 통해 학습 동작을 분석하며, 정규화 스칼라 σ가 암묵적으로 학습률을 감소시켜 학습을 보다 안정적으로 만드는 효과를 보인다는 점을 보여줍니다.
5.2.1 리만 계량
통계 모델의 학습 가능한 파라미터들은 모델의 가능한 모든 입력–출력 관계를 포함하는 부드러운 다양체를 형성합니다. 출력이 확률 분포인 모델의 경우, 이 다양체 상의 두 점 간의 거리를 측정하는 자연스러운 방법은 두 모델 출력 분포 간의 Kullback-Leibler 발산(KL divergence)입니다. KL 발산을 측도로 삼으면, 파라미터 공간은 리만 다양체가 됩니다.

5.2.2 정규화된 일반화 선형 모델의 기하학
본 분석은 일반화 선형 모델(GLM)에 초점을 맞춥니다. 아래의 분석 결과는 Fisher 정보 행렬에 대해 블록 대각선 근사를 사용하는 심층 신경망—각 블록이 단일 뉴런의 파라미터에 해당하는—을 이해하는 데에도 쉽게 적용될 수 있습니다.



가중치 벡터의 크기 증가에 따른 암묵적인 학습률 감소
표준 GLM과 비교할 때, 가중치 벡터 w_i 방향에 대한 F_ij 블록은 게인 파라미터와 정규화 스칼라 σ_i에 의해 스케일 조정됩니다. 만약 w_i의 노름이 두 배로 커지더라도 모델의 출력은 동일하게 유지된다면, Fisher 정보 행렬은 달라지게 됩니다. 이는 역시 두 배가 되어 w_i 방향의 곡률이 1/2로 변화하기 때문입니다. 따라서 정규화된 모델에서 동일한 파라미터 업데이트가 이루어질 때, 가중치 벡터의 노름이 효과적으로 해당 가중치에 대한 학습률을 조절하게 됩니다. 학습 중 노름이 큰 가중치 벡터의 방향을 변경하는 것이 더 어려워지므로, 정규화 기법은 가중치 벡터에 대해 암묵적인 "조기 종료(early stopping)" 효과를 제공하며, 학습이 수렴하도록 안정화하는 데 기여합니다.
들어오는 가중치의 크기 학습
정규화된 모델에서는 들어오는 가중치의 크기가 게인 파라미터에 의해 명시적으로 파라미터화됩니다. 우리는 정규화된 GLM에서 게인 파라미터를 업데이트하는 경우와 원래 파라미터화 하에서 동등한 가중치의 크기를 업데이트하는 경우에 모델 출력이 어떻게 변화하는지 비교합니다. Fˉ 내에서 게인 파라미터 방향은 들어오는 가중치의 크기에 대한 기하학적 구조를 포착합니다. 표준 GLM에서 들어오는 가중치의 크기에 따른 리만 계량은 입력의 노름에 의해 스케일 조정되는 반면, 배치 정규화와 레이어 정규화 모델에서 게인 파라미터의 학습은 오직 예측 오차의 크기에만 의존함을 보입니다. 따라서 정규화된 모델에서 들어오는 가중치의 크기를 학습하는 것은 표준 모델보다 입력 및 그 파라미터의 스케일 변화에 대해 더 강인합니다. (자세한 도출 과정은 부록을 참조하십시오.)
간단하게 말하면, 이 섹션은 정규화가 모델의 파라미터 공간에서 어떻게 작용하는지를 보여줍니다.
- 파라미터 공간의 “거리”
모델의 파라미터를 조금 바꿨을 때 출력이 얼마나 달라지는지를 측정하는 한 가지 방법이 KL 발산을 이용한 리만 계량입니다. 쉽게 말하면, 파라미터가 조금 변할 때 모델의 예측이 얼마나 민감하게 반응하는지를 ‘거리’로 나타낸다고 볼 수 있습니다. - 정규화가 학습률에 미치는 영향
정규화(예: 레이어 정규화)는 뉴런에 들어오는 합산 입력을 평균과 분산을 이용해 조정합니다. 이때 사용되는 스칼라(σ)가 커지면, 실제로 파라미터 업데이트(즉, 가중치 조정)의 효과가 작아집니다. 즉, 큰 가중치를 가진 뉴런은 정규화 덕분에 학습 과정에서 천천히 변화하게 되고, 이는 마치 학습률이 줄어든 것과 같은 효과를 줍니다. - 학습의 안정성 향상
이렇게 정규화가 암묵적으로 학습률을 조절하면서, 가중치의 방향과 크기를 안정적으로 학습할 수 있게 만듭니다. 가중치가 너무 크게 변하거나 너무 빠르게 업데이트되지 않도록 ‘자기 조절’ 효과를 만들어, 학습이 수렴하는 데 도움을 줍니다.
결국, 정규화는 파라미터 공간의 기하학적 특성을 변화시켜, 모델이 더 안정적으로 학습되고, 큰 변화 없이 점진적으로 개선될 수 있도록 돕는다는 것을 이 섹션에서 수식으로 증명하고 있습니다.
6. 실험 결과
본 연구에서는 주로 순환 신경망(RNN)에 초점을 맞춰, 총 6개의 과제(이미지-문장 순위 매기기, 질문-응답, 문맥 언어 모델링, 생성 모델링, 필기체 시퀀스 생성, MNIST 분류)에 대해 레이어 정규화를 적용한 실험을 수행했습니다. 별도의 언급이 없는 한, 실험에서 레이어 정규화의 기본 초기화는 적응형 게인을 1로, 바이어스는 0으로 설정합니다.
6.1 이미지와 언어의 Order Embeddings

(a) Recall@1

(b) Recall@5

(c) Recall@10
그림 1: 레이어 정규화 유무에 따른 order-embeddings를 사용한 Recall@K 곡선

표 2: 캡션 및 이미지 검색에 대한 5개의 테스트 분할에서의 평균 결과. R@K는 Recall@K (값이 클수록 좋음), Mean r는 평균 순위 (값이 작을수록 좋음)를 의미합니다. "Sym"은 대칭 baseline을, "OE"는 order-embeddings를 나타냅니다.
이 실험에서는 Vendrov et al. [2016]에서 제안한 이미지와 문장을 위한 공동 임베딩 공간 학습 모델인 order-embeddings 모델에 레이어 정규화를 적용했습니다. 우리는 Vendrov et al. [2016]의 실험 프로토콜을 그대로 따르고, 공개된 코드를 수정하여 레이어 정규화를 반영하였습니다¹ (https://github.com/ivendrov/order-embedding). 이 코드는 Theano [Team et al., 2016]를 활용합니다. Microsoft COCO 데이터셋 [Lin et al., 2014]의 이미지와 문장은 공통 벡터 공간으로 임베딩되며, 문장은 GRU [Cho et al., 2014]를 사용해 인코딩하고, 미리 학습된 VGG ConvNet [Simonyan and Zisserman, 2015] (10-crop) 출력으로 이미지를 인코딩합니다. order-embeddings 모델은 이미지와 문장을 2단계의 부분 순서로 표현하며, Kiros et al. [2014]에서 사용된 코사인 유사도 대신 비대칭 유사도 함수를 사용합니다.
우리는 두 가지 모델을 훈련시켰습니다. 하나는 baseline order-embedding 모델이고, 다른 하나는 GRU에 레이어 정규화를 적용한 모델입니다. 매 300 반복마다, 별도의 검증 집합에서 Recall@K (R@K) 값을 계산하고, R@K가 개선될 때마다 모델을 저장합니다. 최상의 성능을 보인 모델들은 1000개의 이미지와 5000개의 캡션을 포함한 5개의 별도 테스트 집합에서 평가되며, 그 평균 결과를 보고합니다. 두 모델 모두 동일한 초기 하이퍼파라미터를 사용하는 Adam [Kingma and Ba, 2014]을 사용하며, Vendrov et al. [2016]에서 사용된 동일한 아키텍처 선택으로 훈련됩니다. GRU에 레이어 정규화를 적용하는 방법에 대한 자세한 설명은 부록을 참고하십시오.
그림 1은 레이어 정규화 적용 여부에 따른 모델의 검증 곡선을 보여줍니다. 여기서는 이미지 검색 작업에 대해 R@1, R@5, R@10 값을 플로팅하였습니다. 레이어 정규화를 적용한 경우 모든 평가 지표에서 반복당 속도가 빨라지며, baseline 모델이 최상의 검증 모델에 도달하는 데 걸리는 시간의 60%만 소요함을 확인할 수 있습니다. 또한, 표 2의 테스트 결과에서 볼 수 있듯이, 레이어 정규화를 적용하면 원래 모델에 비해 일반화 성능이 향상됨을 알 수 있습니다. 우리가 보고한 결과는 RNN 임베딩 모델 분야에서 최첨단 성능을 보여주며, Wang et al. [2016]의 구조 보존 모델만이 이 작업에서 더 나은 결과를 보고했지만, 그들은 다른 조건(5개 테스트 집합의 평균 대신 1개의 테스트 집합)에서 평가했으므로 직접 비교하기는 어렵습니다.
6.2 기계에게 읽고 이해하도록 가르치기

그림 2: Attentive reader 모델의 검증 곡선. BN 결과는 [Cooijmans et al., 2016]에서 가져옴.
최근 제안된 순환 배치 정규화 [Cooijmans et al., 2016]와 레이어 정규화를 비교하기 위해, 우리는 Hermann et al. [2015]가 소개한 CNN 코퍼스를 대상으로 단방향(attentive) reader 모델을 훈련시켰습니다. 이 작업은 질문-응답 과제로, 지문에 대한 설명이 주어지고 빈칸을 채워서 답을 만들어내야 합니다. 데이터는 열등한 해결책을 방지하기 위해 익명화되어, 엔티티들이 무작위 토큰으로 치환되고 훈련과 평가 동안 일관되게 순환됩니다.
우리는 [Cooijmans et al., 2016]의 실험 프로토콜을 따르며, 그들의 공개 코드를 수정하여 레이어 정규화를 반영하였습니다² (https://github.com/cooijmanstim/Attentive_reader/tree/bn). 이 코드는 Theano [Team et al., 2016]를 사용합니다. 또한, Hermann et al. [2015]의 원래 실험과 달리, 각 지문이 4문장으로 제한된 전처리 데이터셋을 사용하였습니다.
[Cooijmans et al., 2016]에서는 순환 배치 정규화의 두 가지 변형이 사용되었습니다. 하나는 BN이 LSTM에만 적용되는 경우이고, 다른 하나는 모델 전체에 BN이 적용되는 경우입니다. 본 실험에서는 LSTM 내에만 레이어 정규화를 적용하였습니다.
실험 결과는 그림 2에 나타나 있으며, 레이어 정규화를 적용한 모델이 baseline 및 BN 변형 모두보다 훈련 속도가 빠르고, 더 나은 검증 성능으로 수렴함을 확인할 수 있습니다. [Cooijmans et al., 2016]에서는 BN의 스케일 파라미터를 신중하게 선택해야 하며, 그들의 실험에서는 이를 0.1로 설정했습니다. 반면, 우리는 레이어 정규화에 대해 1.0과 0.1 두 가지 초기 스케일로 실험한 결과, 1.0으로 초기화한 모델이 훨씬 좋은 성능을 보였습니다. 이는 레이어 정규화가 순환 BN과 달리 초기 스케일에 민감하지 않음을 보여줍니다.³
³ [Cooijmans et al., 2016]과 마찬가지로, 본 실험에서는 검증 집합에 대한 결과만을 산출하였습니다.
6.3 Skip-thought 벡터

(a) SICK(𝑟)

(b) SICK(MSE)

(c) MR

(d) CR

(e) SUBJ

(f) MPQA
그림 3: 훈련 반복 횟수에 따른 다운스트림 작업에서 레이어 정규화 적용 유무에 따른 skip-thought 벡터의 성능. 원래의 선은 [Kiros et al., 2015]에서 보고된 결과이며, 에러 막대가 있는 그래프는 10-겹 교차 검증을 사용한 결과입니다. (컬러로 볼 때 가장 잘 보입니다.)
Skip-thoughts [Kiros et al., 2015]는 무감독 방식으로 분산 문장 표현을 학습하기 위한 skip-gram 모델 [Mikolov et al., 2013]의 일반화된 버전입니다. 연속된 텍스트가 주어지면, 한 문장은 인코더 RNN에 의해 인코딩되고, 디코더 RNN들이 주변 문장을 예측하는 데 사용됩니다. Kiros et al. [2015]는 이 모델이 미세 조정 없이도 여러 작업에서 좋은 성능을 보이는 일반적인 문장 표현을 생성할 수 있음을 보여주었으나, 의미 있는 결과를 얻기 위해서는 수일간의 훈련이 필요할 정도로 훈련 시간이 많이 소요됩니다.

표 3: Skip-thoughts 결과. 첫 두 평가 열은 각각 Pearson 상관계수와 Spearman 상관계수를 나타내며, 세 번째 열은 평균 제곱 오차(MSE)를, 나머지 열은 분류 정확도를 나타냅니다. (MSE를 제외한 모든 평가는 값이 클수록 좋습니다.) 우리 모델은 100만 반복(iterations) 동안 훈련되었으며, (†) 표시는 약 1개월(약 170만 반복) 동안 훈련된 모델을 의미합니다.
본 실험에서는 레이어 정규화가 훈련 속도를 얼마나 향상시킬 수 있는지를 조사합니다. 우리는 Kiros et al. [2015]의 공개 코드를 사용하여⁴ (https://github.com/ryankiros/skip-thoughts), BookCorpus 데이터셋 [Zhu et al., 2015]에서 레이어 정규화가 적용된 모델과 적용되지 않은 모델, 두 가지를 훈련시켰습니다. 이 실험은 Theano [Team et al., 2016]를 사용하여 수행되었으며, Kiros et al. [2015]에서 사용한 실험 설정에 따라 동일한 하이퍼파라미터로 2400차원의 문장 인코더를 훈련시켰습니다. 사용된 상태의 크기를 고려할 때, 레이어 정규화가 적용된 경우 반복 당 업데이트 속도가 느려질 수 있을 것으로 예상되지만, CNMeM⁵ (https://github.com/NVIDIA/cnmem)을 사용하면 두 모델 간에 유의미한 차이가 없음을 확인했습니다. 두 모델 모두 50,000 반복마다 체크포인트를 저장하며, 의미 유사도 평가(SICK) [Marelli et al., 2014], 영화 리뷰 감성 분석(MR) [Pang and Lee, 2005], 고객 제품 리뷰(CR) [Hu and Liu, 2004], 주관성/객관성 분류(SUBJ) [Pang and Lee, 2004], 의견 극성 분류(MPQA) [Wiebe et al., 2005]의 다섯 가지 작업에서 성능을 평가하였습니다. 각 체크포인트에서 두 모델의 성능을 모든 작업에 대해 플롯하여 레이어 정규화가 성능 향상 속도를 개선하는지 확인했습니다.
실험 결과는 그림 3에 잘 나타나 있습니다. 그림과 표 3에서 확인할 수 있듯이, 레이어 정규화를 적용하면 baseline에 비해 훈련 속도가 빨라지고, 100만 반복 후의 최종 결과도 개선됩니다. 또한, 레이어 정규화를 적용한 모델을 총 1개월 동안 추가로 훈련시킨 결과, 한 작업을 제외한 모든 작업에서 추가적인 성능 향상이 나타났습니다. 원래 보고된 결과와 우리의 결과 간의 성능 차이는, 공개 코드가 디코더의 각 시간 단계에서 조건화를 수행하지 않는 반면, 원래 모델은 이를 수행한다는 점에서 기인할 가능성이 있음을 주목합니다.
6.4 이진화된 MNIST를 DRAW로 모델링하기

그림 4: 레이어 정규화 적용 유무에 따른 DRAW 모델의 테스트 음의 로그 우도.
또한, 우리는 MNIST 데이터셋을 대상으로 생성 모델링 실험을 진행했습니다. Deep Recurrent Attention Writer (DRAW) [Gregor et al., 2015]는 MNIST 숫자의 분포를 모델링하는 데 있어서 최첨단 성능을 달성한 바 있습니다. 이 모델은 차별화된 주의(attention) 메커니즘과 순환 신경망을 사용하여 이미지의 일부를 순차적으로 생성합니다. 본 실험에서는 64번의 glimpse와 256개의 LSTM 은닉 유닛을 사용하는 DRAW 모델에 레이어 정규화가 미치는 영향을 평가합니다. 모델은 Adam [Kingma and Ba, 2014] 옵티마이저의 기본 설정과 미니 배치 크기 128로 훈련됩니다. 이전 이진화 MNIST 관련 연구들은 데이터셋 생성을 위해 다양한 훈련 프로토콜을 사용했으나, 본 실험에서는 Larochelle과 Murray [2011]의 고정 이진화 방식을 사용하였습니다. 데이터셋은 50,000개의 훈련 이미지, 10,000개의 검증 이미지, 10,000개의 테스트 이미지로 나누어져 있습니다.
그림 4는 첫 100 에포크 동안의 테스트 변분 경계를 보여줍니다. 이를 통해 레이어 정규화를 적용한 DRAW 모델이 baseline 모델에 비해 거의 두 배 빠르게 수렴하는 속도 향상 효과를 확인할 수 있습니다. 200 에포크 후, baseline 모델은 테스트 데이터에서 82.36 nats의 변분 로그 우도에 수렴한 반면, 레이어 정규화 모델은 82.09 nats를 달성하였습니다.
6.5 손글씨 시퀀스 생성

그림 5: 레이어 정규화 적용 유무에 따른 손글씨 시퀀스 생성 모델의 음의 로그 우도. 해당 모델은 미니 배치 크기 8과 시퀀스 길이 500으로 훈련되었습니다.
이전 실험들은 주로 길이가 10에서 40 사이인 NLP 작업의 RNN을 대상으로 진행되었습니다. 보다 긴 시퀀스에서 레이어 정규화의 효과를 보여주기 위해, 우리는 IAM Online Handwriting Database [Liwicki and Bunke, 2005]를 사용하여 손글씨 생성 작업을 수행했습니다. IAM-OnDB는 221명의 서로 다른 필체 작가로부터 수집된 손글씨 줄(line)로 구성되어 있습니다. 주어진 입력 문자 문자열에 대해, 목표는 화이트보드에 기록된 해당 손글씨 줄의 x, y 펜 좌표 시퀀스를 예측하는 것입니다. 전체적으로 12,179개의 손글씨 줄 시퀀스가 있으며, 입력 문자열은 보통 25자 이상이고 평균 손글씨 줄의 길이는 약 700입니다.
우리는 Graves [2013]의 섹션 (5.2)에서 사용된 것과 동일한 모델 아키텍처를 사용했습니다. 이 모델은 400개의 LSTM 셀을 가진 세 개의 은닉층으로 구성되며, 출력 층에서는 20개의 이변량 가우시안 혼합 성분을 생성하고, 입력층의 크기는 3입니다. 문자 시퀀스는 원-핫 벡터로 인코딩되었으므로, 윈도우 벡터의 크기는 57입니다. 윈도우 파라미터를 위해 10개의 가우시안 함수 혼합을 사용하였으며, 이는 크기 30의 파라미터 벡터를 요구합니다. 전체 가중치의 수는 약 370만 개에 달합니다. 모델은 미니 배치 크기 8과 Adam [Kingma and Ba, 2014] 옵티마이저를 사용하여 훈련됩니다.
작은 미니 배치 크기와 매우 긴 시퀀스의 조합은 매우 안정적인 은닉 동역학이 매우 중요함을 의미합니다. 그림 5는 레이어 정규화를 적용한 모델이 baseline 모델과 유사한 로그 우도에 수렴하면서도 훨씬 빠르게 수렴함을 보여줍니다.
6.6 Permutation invariant MNIST
RNN뿐 아니라 피드포워드 네트워크에서도 레이어 정규화를 조사하였습니다. 본 연구에서는 잘 알려진 permutation invariant MNIST 분류 문제에서 레이어 정규화가 배치 정규화와 어떻게 비교되는지를 보여줍니다. 이전 분석에서, 레이어 정규화는 내부 은닉층에 대해 입력 재스케일링에 불변하도록 동작하는데, 이는 바람직한 특성입니다. 다만, 예측 신뢰도가 logit의 스케일에 의해 결정되는 logit 출력에서는 이러한 불변성이 필요하지 않으므로, 마지막 softmax 층을 제외한 완전 연결 은닉층에만 레이어 정규화를 적용합니다.
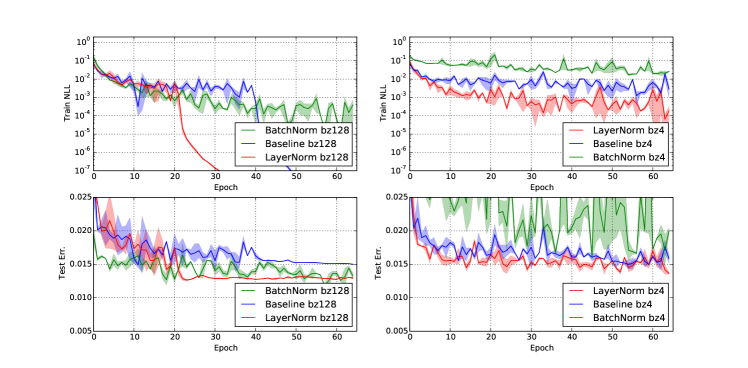
그림 6: 레이어 정규화와 배치 정규화를 적용한 permutation invariant MNIST 784-1000-1000-10 모델의 음의 로그 우도 및 테스트 오류. (왼쪽) 모델은 배치 크기 128로 훈련되었고, (오른쪽) 모델은 배치 크기 4로 훈련되었습니다.
모든 모델은 55,000개의 훈련 데이터를 사용하고 Adam [Kingma and Ba, 2014] 옵티마이저로 훈련되었습니다. 배치 크기가 작은 경우, 배치 정규화의 분산 항은 불편 추정량을 사용하여 계산됩니다. 그림 6의 실험 결과는 레이어 정규화가 배치 크기에 대해 강건하며, 모든 층에 적용된 배치 정규화에 비해 훨씬 빠른 훈련 수렴 속도를 보인다는 점을 강조합니다.
6.7 합성곱 신경망
우리는 또한 합성곱 신경망(Convolutional Neural Networks)을 대상으로 실험을 진행했습니다. 초기 실험에서, 레이어 정규화는 정규화가 적용되지 않은 baseline 모델에 비해 속도 향상을 제공하는 것으로 관찰되었으나, 배치 정규화가 다른 방법들보다 더 뛰어난 성능을 보였습니다. 완전 연결층에서는 한 층의 모든 은닉 유닛들이 최종 예측에 유사한 기여를 하는 경향이 있어, 한 층의 합산 입력을 재중심화하고 재스케일링하는 것이 잘 작동합니다. 그러나 합성곱 신경망에서는 이러한 유사한 기여 가정이 더 이상 성립하지 않습니다. 이미지 경계 근처에 위치한 많은 은닉 유닛들은 거의 활성화되지 않아, 동일한 층 내 다른 은닉 유닛들과 매우 다른 통계적 특성을 보입니다. 이에 따라, 합성곱 신경망에서 레이어 정규화를 효과적으로 활용하기 위해서는 추가 연구가 필요하다고 생각합니다.
7 결론
본 논문에서는 신경망 훈련 속도를 향상시키기 위해 레이어 정규화를 도입하였습니다. 우리는 레이어 정규화와 배치 정규화, 그리고 weight normalization의 불변성 특성을 비교하는 이론적 분석을 제시하였으며, 레이어 정규화가 각 훈련 사례별 특징의 이동과 스케일 변화에 대해 불변임을 보였습니다.
또한, 실험적으로 순환 신경망은 특히 긴 시퀀스와 작은 미니 배치에서 제안한 방법으로부터 가장 큰 혜택을 받는다는 것을 확인하였습니다.
이 논문에서 제시된 이론과 실험 결과를 보면, layer normalization이 입력의 스케일과 중심을 안정화시켜 학습 속도를 높이고, 특히 긴 시퀀스나 작은 미니 배치 상황에서 매우 효과적임을 알 수 있습니다. Transformer와 GPT 계열 모델에서는 각 레이어의 출력이 안정적이어야 하며, 배치 크기에 민감하지 않은 정규화 방식이 필요하기 때문에 layer norm을 사용합니다. 이로 인해 모델이 더 빠르게 수렴하고, 학습이 안정적으로 이루어질 수 있습니다.
'인공지능' 카테고리의 다른 글
| Large Language Diffusion Models (2) | 2025.02.18 |
|---|---|
| DeepSeek-V3 Technical Report (2) | 2025.02.14 |
| DeepSeek-R1: Incentivizing Reasoning Capability in LLMs via Reinforcement Learning (2) | 2025.02.12 |
| Instance Normalization: The Missing Ingredient for Fast Stylization (3) | 2025.01.30 |
| Group Normalization (2) | 2025.01.24 |



