Intuitive understanding of 1D, 2D, and 3D convolutions in convolutional neural networks [closed]

https://stackoverflow.com/questions/42883547/intuitive-understanding-of-1d-2d-and-3d-convolutions-in-convolutional-neural-n

 

conv에 대해서 햇갈리는 사람이 꽤 있을 것이다. 그런점에서 이 글이 괜찮은것 같아서 가져왔다.

 

C3D에서 가져온 그림을 활용해서 설명하고 싶습니다.

한마디로 요약하자면, 합성곱의 방향성과 출력 형태(output shape) 가 매우 중요합니다!

↑↑↑↑↑ 1D 합성곱 - 기본 형태 ↑↑↑↑↑

• 단일 방향(시간 축)으로만 합성곱을 계산합니다.
• 입력: [W], 필터: [k], 출력: [W]
• 예시)
  입력 = [1, 1, 1, 1, 1]
  필터 = [0.25, 0.5, 0.25]
  출력 = [1, 1, 1, 1, 1]
• 출력 형태는 1차원 배열입니다.
• 예: 그래프 스무딩(graph smoothing)에 사용 가능

tf.nn.conv1d 코드 예시 (Toy Example)

import tensorflow as tf
import numpy as np

sess = tf.Session()

ones_1d = np.ones(5)
weight_1d = np.ones(3)
strides_1d = 1

in_1d = tf.constant(ones_1d, dtype=tf.float32)
filter_1d = tf.constant(weight_1d, dtype=tf.float32)

in_width = int(in_1d.shape[0])
filter_width = int(filter_1d.shape[0])

input_1d   = tf.reshape(in_1d, [1, in_width, 1])
kernel_1d  = tf.reshape(filter_1d, [filter_width, 1, 1])
output_1d  = tf.squeeze(tf.nn.conv1d(input_1d, kernel_1d, strides_1d, padding='SAME'))

print(sess.run(output_1d))

↑↑↑↑↑ 2D 합성곱 - 기본 형태 ↑↑↑↑↑

• 두 방향(x, y)으로 합성곱을 계산
• 출력 형태는 2차원 행렬(Matrix)
• 입력 = [W, H], 필터 = [k, k], 출력 = [W, H]
• 예시: Sobel 엣지 필터

tf.nn.conv2d 코드 예시 (Toy Example)

ones_2d = np.ones((5,5))
weight_2d = np.ones((3,3))
strides_2d = [1, 1, 1, 1]

in_2d = tf.constant(ones_2d, dtype=tf.float32)
filter_2d = tf.constant(weight_2d, dtype=tf.float32)

in_width = int(in_2d.shape[0])
in_height = int(in_2d.shape[1])

filter_width = int(filter_2d.shape[0])
filter_height = int(filter_2d.shape[1])

input_2d   = tf.reshape(in_2d, [1, in_height, in_width, 1])
kernel_2d  = tf.reshape(filter_2d, [filter_height, filter_width, 1, 1])

output_2d  = tf.squeeze(tf.nn.conv2d(input_2d, kernel_2d, strides=strides_2d, padding='SAME'))

print(sess.run(output_2d))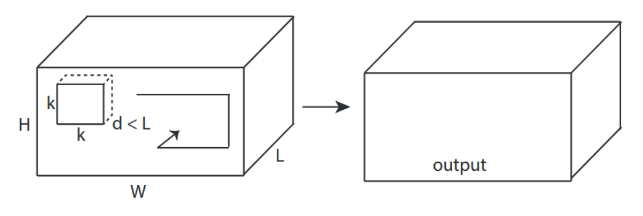

↑↑↑↑↑ 3D 합성곱 - 기본 형태 ↑↑↑↑↑

• 세 방향(x, y, z)으로 합성곱 계산
• 출력 형태는 3차원 볼륨(Volume)
• 입력 = [W, H, L], 필터 = [k, k, d], 출력 = [W, H, M]
• 이때 중요한 조건: d < L
  → 필터 깊이(d)가 입력 깊이(L)보다 작아야 출력 볼륨이 생성됨
• 예시: C3D (3D ConvNet for video)

tf.nn.conv3d – 3D 합성곱 예제 (Toy Example)

ones_3d = np.ones((5,5,5))
weight_3d = np.ones((3,3,3))
strides_3d = [1, 1, 1, 1, 1]

in_3d = tf.constant(ones_3d, dtype=tf.float32)
filter_3d = tf.constant(weight_3d, dtype=tf.float32)

in_width = int(in_3d.shape[0])
in_height = int(in_3d.shape[1])
in_depth = int(in_3d.shape[2])

filter_width = int(filter_3d.shape[0])
filter_height = int(filter_3d.shape[1])
filter_depth = int(filter_3d.shape[2])

input_3d   = tf.reshape(in_3d, [1, in_depth, in_height, in_width, 1])
kernel_3d  = tf.reshape(filter_3d, [filter_depth, filter_height, filter_width, 1, 1])

output_3d  = tf.squeeze(tf.nn.conv3d(input_3d, kernel_3d, strides=strides_3d, padding='SAME'))
print(sess.run(output_3d))

↑↑↑↑↑ 2D 합성곱 + 3D 입력 - LeNet, VGG 등에서 사용되는 구조 ↑↑↑↑↑

• 입력이 3D일지라도 (예: 224×224×3, 112×112×32),
  출력은 3D 볼륨이 아닌 2D 행렬 형태입니다.
• 그 이유는 필터의 깊이(L)가 입력 채널 수와 일치해야 하며,
  실제 연산은 x, y 방향 (2D) 으로만 수행되기 때문입니다.
• 입력: [W, H, L], 필터: [k, k, L], 출력: [W, H]
• 여러 개의 필터(N)를 사용하면, 출력은 2D 결과들을 스택한 형태, 즉
  3D = (2D × N) 형태가 됩니다.

conv2d – LeNet, VGG 구조에서 1개의 필터 사용하는 예제

in_channels = 32  # 예: RGB = 3, 그 이후 32, 64, 128 등
ones_3d = np.ones((5, 5, in_channels))
weight_3d = np.ones((3, 3, in_channels))
strides_2d = [1, 1, 1, 1]

in_3d = tf.constant(ones_3d, dtype=tf.float32)
filter_3d = tf.constant(weight_3d, dtype=tf.float32)

input_3d  = tf.reshape(in_3d, [1, 5, 5, in_channels])
kernel_3d = tf.reshape(filter_3d, [3, 3, in_channels, 1])

output_2d = tf.squeeze(tf.nn.conv2d(input_3d, kernel_3d, strides=strides_2d, padding='SAME'))
print(sess.run(output_2d))

conv2d – LeNet, VGG 구조에서 여러 개의 필터(N) 사용하는 예제

in_channels = 32
out_channels = 64
ones_3d = np.ones((5, 5, in_channels))
weight_4d = np.ones((3, 3, in_channels, out_channels))
strides_2d = [1, 1, 1, 1]

in_3d = tf.constant(ones_3d, dtype=tf.float32)
filter_4d = tf.constant(weight_4d, dtype=tf.float32)

input_3d  = tf.reshape(in_3d, [1, 5, 5, in_channels])
kernel_4d = tf.reshape(filter_4d, [3, 3, in_channels, out_channels])

output_3d = tf.nn.conv2d(input_3d, kernel_4d, strides=strides_2d, padding='SAME')
print(sess.run(output_3d))

출력은 2D × N 형태로 스택된 3D 텐서입니다.
(N은 필터 개수)

 

↑↑↑↑↑ 보너스: 1×1 합성곱 (GoogLeNet 등에서 사용) ↑↑↑↑↑

• 1×1 합성곱은 sobel 같은 전통적 2D 필터처럼 생각하면 혼동될 수 있습니다.
• CNN에서의 1×1 합성곱은 깊이 방향(depth-wise) 연산입니다.
• 입력: [W, H, L], 필터: [1, 1, L], 출력: [W, H]
• 여러 개의 필터를 사용할 경우, 출력은 2D × N = 3D 형태입니다.

1×1 conv 예제 (tf.nn.conv2d 사용)

in_channels = 32
out_channels = 64
ones_3d = np.ones((1, 1, in_channels))
weight_4d = np.ones((1, 1, in_channels, out_channels))
strides_2d = [1, 1, 1, 1]

in_3d = tf.constant(ones_3d, dtype=tf.float32)
filter_4d = tf.constant(weight_4d, dtype=tf.float32)

input_3d  = tf.reshape(in_3d, [1, 1, 1, in_channels])
kernel_4d = tf.reshape(filter_4d, [1, 1, in_channels, out_channels])

output_3d = tf.nn.conv2d(input_3d, kernel_4d, strides=strides_2d, padding='SAME')
print(sess.run(output_3d))

 

📽 애니메이션: 3D 입력에 대한 2D 합성곱 (2D Conv with 3D-inputs)

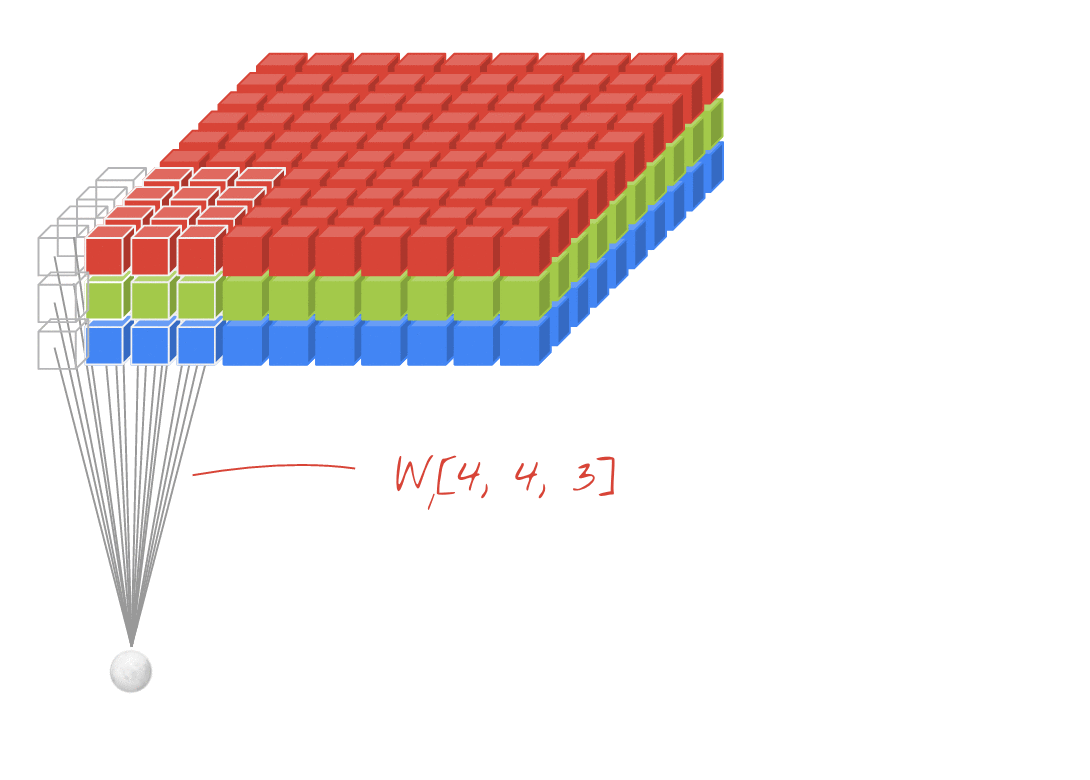
• 원본 링크: LINK
• 작성자: Martin Görner
• Twitter: @martin_gorner
• Google+: plus.google.com/+MartinGorne

New community features for Google Chat and an update on Currents

🎁 보너스: 2D 입력에 대한 1D 합성곱

↑↑↑↑↑ 1D 입력에 대한 1D 합성곱 ↑↑↑↑↑

↑↑↑↑↑ 2D 입력에 대한 1D 합성곱 ↑↑↑↑↑

• 입력이 2D (예: 20×14)일지라도, 출력은 2D가 아니라 1D 행렬입니다.
• 그 이유는 필터의 높이 L이 입력의 높이 L과 같아야 하며, 연산은 x 방향(1D) 으로만 수행되기 때문입니다.
• 입력: [W, L], 필터: [k, L], 출력: [W]
• 출력 형태: 1D 벡터

💡 여러 개의 필터(N)를 사용한다면?
→ 출력은 1D × N = 2D 형태로 스택됩니다.

 

🎁 보너스: C3D 구조를 위한 3D 합성곱 예제

in_channels = 32  # 예: RGB=3 또는 32, 64, 128 등
out_channels = 64
ones_4d = np.ones((5,5,5,in_channels))  # 입력: (W, H, D, in_channels)
weight_5d = np.ones((3,3,3,in_channels,out_channels))  # 필터: (k, k, k, in_channels, out_channels)
strides_3d = [1, 1, 1, 1, 1]

in_4d = tf.constant(ones_4d, dtype=tf.float32)
filter_5d = tf.constant(weight_5d, dtype=tf.float32)

input_4d  = tf.reshape(in_4d, [1, 5, 5, 5, in_channels])
kernel_5d = tf.reshape(filter_5d, [3, 3, 3, in_channels, out_channels])

output_4d = tf.nn.conv3d(input_4d, kernel_5d, strides=strides_3d, padding='SAME')
print(sess.run(output_4d))

sess.close()

📥 TensorFlow에서의 입력과 출력

 

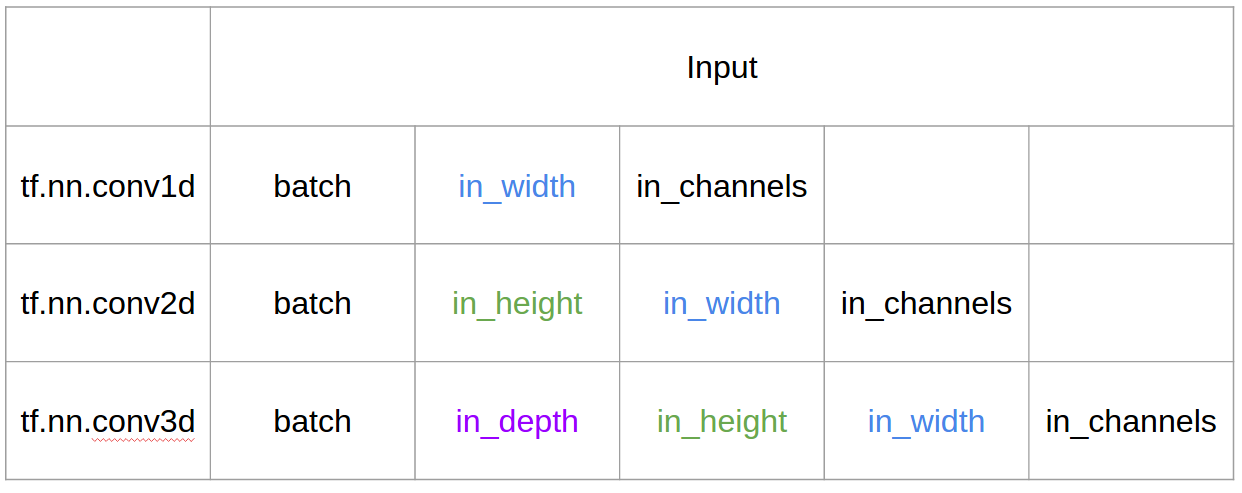
🧾 요약 (Summary)

 

---

 

@runhani님의 답변에 이어, 설명을 좀 더 명확히 하고자 몇 가지 내용을 추가하고 예제도 TF1과 TF2 기준으로 함께 소개해 보겠습니다.

 

이번에 추가로 강조하고 싶은 핵심 내용은 다음과 같습니다:

• 적용 사례(application) 강조
• tf.Variable 사용법
• 1D/2D/3D 합성곱에서 입력, 커널, 출력 구조에 대한 더 명확한 설명
• stride(보폭), padding(패딩)의 영향

✅ 1D 합성곱 (1D Convolution)

다음은 TensorFlow 1.x 및 TensorFlow 2.x에서 1D 합성곱을 구현하는 예제입니다.

📐 데이터 형태 (Shape)

• 입력 벡터 (1D): [배치 크기, 너비, 입력 채널 수] 예: (1, 5, 1)
• 커널 (필터): [커널 너비, 입력 채널 수, 출력 채널 수] 예: (5, 1, 4)
• 출력: [배치 크기, 너비, 출력 채널 수] 예: (1, 5, 4)

🧪 TF1 예제

import tensorflow as tf
import numpy as np

# 입력 플레이스홀더 선언
inp = tf.placeholder(shape=[None, 5, 1], dtype=tf.float32)

# 커널 가중치 변수 선언
kernel = tf.Variable(tf.initializers.glorot_uniform()([5, 1, 4]), dtype=tf.float32)

# 1D 합성곱 연산
out = tf.nn.conv1d(inp, kernel, stride=1, padding='SAME')

# 세션 실행
with tf.Session() as sess:
  tf.global_variables_initializer().run()
  print(sess.run(out, feed_dict={
    inp: np.array([
      [[0],[1],[2],[3],[4]],
      [[5],[4],[3],[2],[1]]
    ])
  }))

🧪 TF2 예제

import tensorflow as tf
import numpy as np

# 입력 데이터
inp = np.array([
  [[0],[1],[2],[3],[4]],
  [[5],[4],[3],[2],[1]]
]).astype(np.float32)

# 커널 변수 정의
kernel = tf.Variable(tf.initializers.glorot_uniform()([5, 1, 4]), dtype=tf.float32)

# 1D 합성곱
out = tf.nn.conv1d(inp, kernel, stride=1, padding='SAME')
print(out)

🔍 참고 사항

• TensorFlow 2에서는 Session이나 variable_initializer() 같은 절차가 필요 없기 때문에 훨씬 간단하게 구현할 수 있습니다.
• 위의 예제는 실전에서 커널의 출력 채널 수(out_channels)를 다르게 설정하여 다양한 특성 맵을 학습하는 데 응용할 수 있습니다.
• stride, padding 설정에 따라 출력의 크기와 특성도 달라지니 실험적으로 확인해보는 것도 좋습니다.

필요하다면 2D 또는 3D 버전도 이어서 설명해 드릴 수 있습니다.

 

📌 실제 상황에서는 어떻게 보일까요?

이번엔 신호 스무딩(signal smoothing) 예제를 통해 이 연산이 실제로 무엇을 하는지 살펴보겠습니다.

• 왼쪽에는 원본 신호,
• 오른쪽에는 출력 채널이 3개인 1D 합성곱 결과가 표시되어 있습니다.

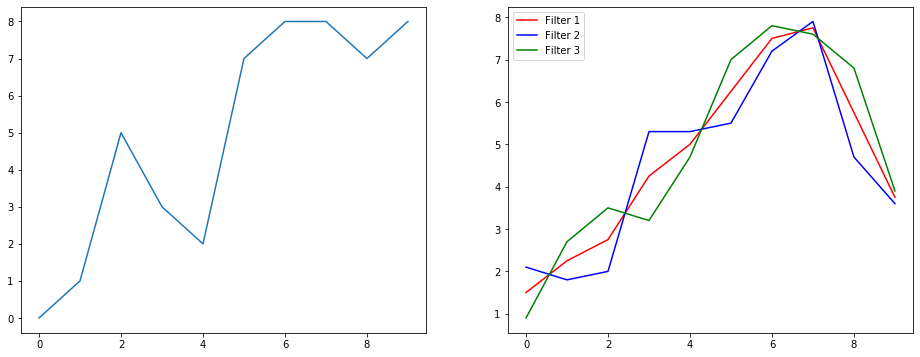
💡 여러 채널이 의미하는 것은?

여러 채널은 입력에 대해 다양한 특성(feature)을 추출한 표현을 의미합니다.
이 예제에서는 세 개의 서로 다른 필터를 사용하여, 입력 신호로부터 세 가지 표현을 만들어냅니다.

• 첫 번째 채널: 모든 위치에 동일한 가중치를 적용한 스무딩 필터
• 두 번째 채널: 중앙에 더 큰 가중치를 주고, 양 끝은 덜 반영하는 필터
• 세 번째 채널: 두 번째와 반대로 양 끝에 더 큰 가중치를 주는 필터

이처럼, 각 필터는 서로 다른 방식으로 입력을 처리하며, 결과적으로 서로 다른 효과를 만들어냅니다.

 

🧠 딥러닝에서 1D 합성곱의 활용

1D Convolution은 특히 문장 분류(sentence classification) 과 같은 자연어 처리(NLP) 문제에서 성공적으로 활용되어 왔습니다. 예를 들어, 각 단어를 임베딩한 후, 1D 합성곱을 통해 문장 내 중요한 n-gram 패턴을 포착할 수 있습니다. 필요하다면 자연어 처리에서 1D Conv 사용 사례를 더 구체적으로 소개해 드릴 수도 있어요.

 

🧱 2D 합성곱 (2D Convolution)

이제 2D 합성곱으로 넘어가 봅시다. 딥러닝을 해본 사람이라면 2D Convolution을 한 번도 본 적 없다는 건... 거의 불가능하겠죠.

2D 합성곱은 이미지 분류, 객체 탐지 같은 CNN(Convolutional Neural Network) 에서 핵심적으로 사용되며, 이미지를 포함한 NLP 문제(예: 이미지 캡션 생성)에도 쓰입니다.

 

🔍 예제: 필터 3종 적용

아래와 같은 3×3 커널(필터)을 사용할 것입니다:

1. 에지(Edge) 감지 필터
2. 블러(Blur) 필터
3. 샤프닝(Sharpen) 필터

입력 및 출력 형태

• 이미지 (흑백): [배치 크기, 높이, 너비, 채널 수] → 예: (1, 340, 371, 1)
• 커널 (필터): [높이, 너비, 입력 채널 수, 출력 채널 수] → 예: (3, 3, 1, 3)
• 출력 (특성 맵): [배치 크기, 높이, 너비, 출력 채널 수] → 예: (1, 340, 371, 3)

🧪 TF1 예제

import tensorflow as tf
import numpy as np
from PIL import Image

# 흑백 이미지 불러오기
im = np.array(Image.open(<some image>).convert('L'))  # /255.0 생략 가능

# 3개의 필터 정의: 에지, 블러, 샤프닝
kernel_init = np.array([
  [[[-1, 1.0/9, 0]], [[-1, 1.0/9, -1]], [[-1, 1.0/9, 0]]],
  [[[-1, 1.0/9, -1]], [[8, 1.0/9, 5]], [[-1, 1.0/9, -1]]],
  [[[-1, 1.0/9, 0]], [[-1, 1.0/9, -1]], [[-1, 1.0/9, 0]]]
])

image_height, image_width = im.shape

inp = tf.placeholder(shape=[None, image_height, image_width, 1], dtype=tf.float32)
kernel = tf.Variable(kernel_init, dtype=tf.float32)

out = tf.nn.conv2d(inp, kernel, strides=[1, 1, 1, 1], padding='SAME')

with tf.Session() as sess:
  tf.global_variables_initializer().run()
  res = sess.run(out, feed_dict={inp: np.expand_dims(np.expand_dims(im, 0), -1)})

🧪 TF2 예제

import tensorflow as tf
import numpy as np
from PIL import Image

im = np.array(Image.open(<some image>).convert('L'))  # /255.0 생략 가능
x = np.expand_dims(np.expand_dims(im, 0), -1)

kernel_init = np.array([
  [[[-1, 1.0/9, 0]], [[-1, 1.0/9, -1]], [[-1, 1.0/9, 0]]],
  [[[-1, 1.0/9, -1]], [[8, 1.0/9, 5]], [[-1, 1.0/9, -1]]],
  [[[-1, 1.0/9, 0]], [[-1, 1.0/9, -1]], [[-1, 1.0/9, 0]]]
])

kernel = tf.Variable(kernel_init, dtype=tf.float32)
out = tf.nn.conv2d(x, kernel, strides=[1, 1, 1, 1], padding='SAME')

 

📸 실제 출력은 어떤 모습일까?

위 코드를 실행하면 다음과 같은 결과를 확인할 수 있습니다:

• 첫 번째 이미지: 원본
• 그 이후 시계 방향으로: 필터 1번, 2번, 3번을 각각 적용한 출력

💡 여러 채널은 무엇을 의미할까?

2D 합성곱에서는 "여러 채널" 개념이 직관적으로 이해됩니다.
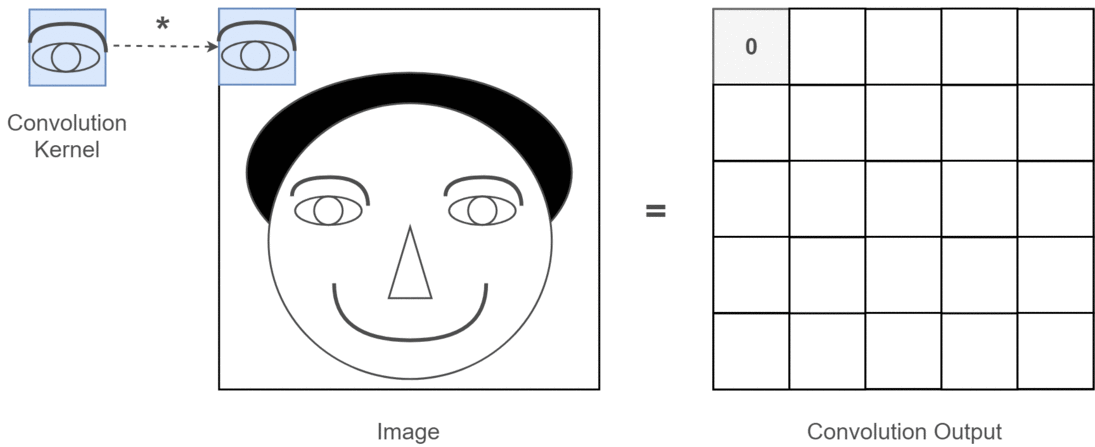
예를 들어, 얼굴 인식(Face Recognition)을 생각해봅시다.

• 각 필터는 눈, 코, 입 등 얼굴의 특정 특징을 감지하는 역할을 한다고 할 수 있습니다.
• 그러면 출력 특성 맵(feature map)은 각 특징이 이미지에 존재하는지를 이진적으로 표현할 수 있습니다.

이러한 특성은 얼굴 인식 모델에 매우 중요한 정보가 되며,
딥러닝 모델이 학습 과정에서 직접 이러한 필터를 자동으로 학습하게 됩니다.

 

 

📚 2D 합성곱의 딥러닝 활용 사례

• CNN(Convolutional Neural Networks) 에서는 거의 모든 컴퓨터 비전 과제에서
  2D 합성곱 연산이 사용됩니다.
  • 이미지 분류 (Image Classification)
  • 객체 탐지 (Object Detection)
  • 동영상 분류 (Video Classification)
  • 이미지 생성 및 보정 (e.g., GAN, Super Resolution)

🧊 3D 합성곱 (3D Convolution)

차원이 증가할수록 시각적으로 표현하기는 점점 어려워지지만, 1D와 2D 합성곱을 잘 이해했다면 3D 합성곱도 쉽게 일반화할 수 있습니다.

 

📐 데이터 형태

• 3D 입력 데이터 (예: LIDAR):
  [배치 크기, 높이, 너비, 깊이, 입력 채널 수]
  예: (1, 200, 200, 200, 1)
• 커널 (필터):
  [높이, 너비, 깊이, 입력 채널 수, 출력 채널 수]
  예: (5, 5, 5, 1, 3)
• 출력:
  [배치 크기, 높이, 너비, 깊이, 출력 채널 수]
  예: (1, 200, 200, 200, 3)

🧪 TF1 예제

import tensorflow as tf
import numpy as np

tf.reset_default_graph()

inp = tf.placeholder(shape=[None, 200, 200, 200, 1], dtype=tf.float32)
kernel = tf.Variable(tf.initializers.glorot_uniform()([5, 5, 5, 1, 3]), dtype=tf.float32)

out = tf.nn.conv3d(inp, kernel, strides=[1, 1, 1, 1, 1], padding='SAME')

with tf.Session() as sess:
    tf.global_variables_initializer().run()
    res = sess.run(out, feed_dict={inp: np.random.normal(size=(1, 200, 200, 200, 1))})

 

🧪 TF2 예제

import tensorflow as tf
import numpy as np

x = np.random.normal(size=(1, 200, 200, 200, 1))
kernel = tf.Variable(tf.initializers.glorot_uniform()([5, 5, 5, 1, 3]), dtype=tf.float32)

out = tf.nn.conv3d(x, kernel, strides=[1, 1, 1, 1, 1], padding='SAME')

 

🧠 딥러닝에서 3D 합성곱의 활용

3D 합성곱은 주로 3차원 데이터를 다루는 머신러닝/딥러닝 분야에서 사용됩니다. 대표적으로는 LIDAR (Light Detection and Ranging) 와 같은 3차원 센서 데이터를 처리할 때 많이 활용됩니다.

 

🧩 추가 개념: Stride와 Padding

이제 거의 다 왔습니다! 자, stride(스트라이드) 와 padding(패딩) 이 무엇인지 이해해 봅시다.

 

🦶 스트라이드(stride)의 의미

스트라이드는 말 그대로 "몇 칸씩 건너뛸 것인가"를 의미합니다. 복도를 큰 보폭(stride)으로 걷는다면 더 빨리 도착할 수 있지만,
그만큼 주변을 덜 관찰하게 됩니다.

• 2D 합성곱에서 stride는 [배치, 높이, 너비, 채널] 순서입니다. 일반적으로 배치와 채널 방향 스트라이드는 1로 고정합니다.
  → 결국 설정할 건 높이, 너비 방향의 stride 두 개뿐입니다.
• 3D 합성곱에서는 [배치, 높이, 너비, 깊이, 채널] 순서입니다. 마찬가지로, 높이/너비/깊이 방향의 stride만 신경 쓰면 됩니다.

🧱 패딩(padding)의 의미

stride가 1이더라도, 합성곱 연산 과정에서 출력 크기가 줄어드는 현상은 피할 수 없습니다.
예를 들어, 너비가 4인 입력에 커널을 적용하면 출력은 너비 3이 됩니다.
→ 이처럼 차원이 점점 줄어드는 현상은 깊은 네트워크에서는 원치 않는 경우가 많습니다.

이를 해결하는 방식이 바로 패딩입니다.

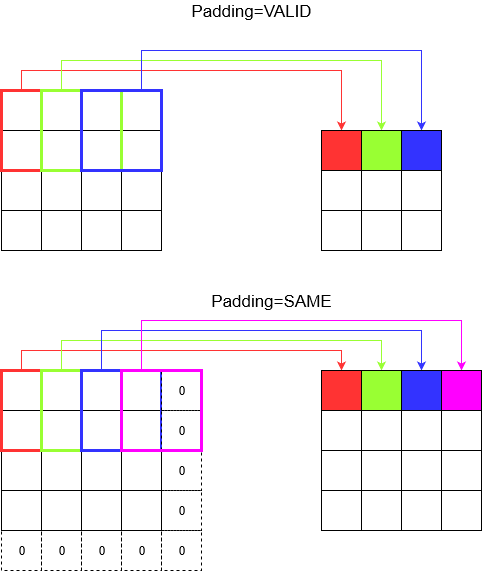
• SAME: 출력 크기를 입력과 같게 유지함
• VALID: 패딩 없이 필터가 실제 데이터 위에서만 연산되므로 출력 크기 감소

💬 마지막 정리

혹시 궁금할 수도 있습니다.
"방금까지 자동으로 줄어드는 차원에 대해 설명하더니, 이제 stride로 다시 조절한다고?"
→ 맞습니다. 스트라이드는 출력 크기를 어떻게, 언제, 얼마나 줄일지 직접 제어할 수 있는 도구입니다.
즉, 차원 축소를 통제할 수 있다는 점에서 매우 강력합니다.