PlatoNeRF: 3D Reconstruction in Plato's Cave via Single-View Two-Bounce Lidar
PlatoNeRF: 3D Reconstruction in Plato's Cave via Single-View Two-Bounce Lidar
platonerf.github.io
요약
단일 뷰에서 3D 재구성은 단안 단서의 모호성과 가려진 영역에 대한 정보 부족으로 인해 어려운 과제입니다. 뉴럴 방사 필드(NeRF)는 뷰 합성 및 3D 재구성에 널리 사용되지만, 일반적으로 다중 뷰 이미지를 필요로 합니다. 단일 뷰 3D 재구성을 위한 기존의 NeRF 방법들은 가려진 영역의 뷰를 상상하기 위해 데이터 사전 지식을 사용하거나, RGB 카메라로 관찰되는 그림자를 이용하는데, 이는 주변 조명과 낮은 반사율 배경에서 감지하기 어렵습니다. 우리는 이러한 한계를 극복하기 위해 단일-광자 에벌랜치 다이오드로 캡처한 시간 비행 데이터를 사용할 것을 제안합니다. 우리의 방법은 NeRF로 이중 반사 광 경로를 모델링하고, 라이다 일시적 데이터를 감독 데이터로 사용합니다. NeRF와 라이다로 측정된 이중 반사 광의 장점을 활용하여, 데이터 사전 지식 없이 또는 제어된 주변 조명이나 장면 반사율에 의존하지 않고도 가시 및 가려진 기하학을 재구성할 수 있음을 보여줍니다. 추가로, 센서의 공간 및 시간 해상도에 대한 실용적 제약 조건 하에서 개선된 일반화를 보여줍니다. 단일-광자 라이다가 휴대폰, 태블릿 및 헤드셋과 같은 소비자 기기에서 보편화됨에 따라 우리의 방법이 유망한 방향이라고 믿습니다.

그림 1. PlatoNeRF. 단일 광자 라이다로 캡처한 투바운스 신호를 사용하여 단일 뷰에서 장면 형상을 복구하는 방법인 PlatoNeRF를 제안합니다. (a) 레이저가 장면 지점을 비추면 모든 방향으로 빛을 확산 반사합니다. 반사된 빛은 장면의 나머지 부분을 비추고 그림자를 드리웁니다. 라이다 센서로 돌아오는 빛은 보이는 장면에 대한 정보를 제공하고, 그림자는 가려진 장면에 대한 정보를 제공합니다. (b) 라이다 센서가 3D ToF(Time-of-Flight) 이미지를 캡처합니다. (c) 레이저의 위치를 스캔하여 이러한 여러 이미지를 집계함으로써 볼류메트릭 렌더링으로 전체 3D 장면 지오메트리를 재구성할 수 있습니다.
1. 소개
단일 뷰에서 3D 장면 기하학을 복원하는 것은 자율 주행 차량(AV)에서 확장 현실(XR)에 이르는 많은 응용 분야에 필수적입니다. XR에서 가상의 공과 캐치볼을 하는 상황을 생각해보십시오. 만약 공이 떨어져서 소파 뒤에서 튕긴다면, 그 공은 가려진 기하학에 따라 물리적으로 현실적인 방식으로 튕겨 나와야 합니다. XR 사용자에게 장면의 완전하고 최신 상태의 스캔을 유지하는 것은 번거롭고, 로봇 공학 및 AV와 같은 다른 많은 응용 분야에서는 실현 불가능합니다. 따라서 단일 또는 소수의 뷰에서 기하학을 복원하는 방법이 필요하며, 우리는 단일 뷰의 문제를 다룹니다.
뉴럴 방사 필드(NeRF)는 장면 기하학을 표현하는 데 인기 있지만, 단일 뷰 3D 재구성은 여전히 도전적이고 미해결 문제로 남아 있습니다. 단일 뷰 3D 재구성을 위한 기존 NeRF 방법들은 데이터 사전 지식에 의존하거나 시각적 단서, 예를 들어 그림자를 사용하여 단일 뷰에서 가려진 기하학을 추론합니다. 확산, 생성적 적대 신경망 및 트랜스포머와 같은 접근 방식은 관찰과 대규모 훈련 데이터 간의 상관관계를 활용하기 위해 데이터 사전 지식에 의존합니다. 결과적으로 이러한 방법은 통계적으로 가능성 있는 내용을 상상할 수 있지만, 물리적으로 정확하지 않을 수 있습니다. 다른 방법들은 NeRF를 훈련할 때 그림자를 사용하여 가려진 기하학을 추론하지만, 이러한 방법들은 주변 조명이나 낮은 반사율 배경에서 그림자를 감지하기 어려운 경우에 어려움을 겪습니다. 또한, 이러한 방법들은 일반적으로 절대 깊이보다는 상대 깊이를 예측하며, 이는 많은 응용 분야에서 중요합니다.
이러한 한계를 극복하면서도 물리적으로 정확한 재구성을 가능하게 하기 위해, 우리는 라이다로 측정된 이중 반사 빛을 사용하는 것을 제안합니다. 단일-광자 에벌랜치 다이오드(SPAD)로 구현된 단일-광자 라이다 시스템은 정확한 단일 뷰 3D 재구성을 위한 기회를 제공합니다. 라이다 시스템은 일반적으로 장면으로 빛을 방출하고 센서로 돌아오는 빛의 비행 시간을 측정합니다. 이 빛은 장면에서 여러 번 반사되며, 우리는 각 반사를 "반사"라고 부릅니다. 기존의 라이다 시스템은 장면에서 센서로 돌아오는 첫 번째 반사 빛만을 이용하여 정확한 절대 깊이를 제공하지만, 최근 연구는 이중 반사 비행 시간, 즉 빛이 장면에서 두 번 반사되어 센서로 돌아오는 시간을 이용하여 가려진 물체를 재구성할 수 있음을 보여주었습니다. 그러나 기존 방법의 한계는 소비자 기기에서 발견되는 라이다의 낮은 공간 및 시간 해상도에 대한 일반화입니다.
우리의 방법인 PlatoNeRF는 이중 반사 라이다와 NeRF의 한계를 모두 해결합니다. PlatoNeRF의 목표는 단일-광자 라이다의 이중 반사 빛의 비행 시간 측정을 사용하여 단일 뷰에서 가시 및 가려진 기하학을 재구성하는 것입니다. Henley et al.의 연구와 같이, 우리는 장면의 개별 지점을 펄스 레이저로 조명합니다. 빛은 조명된 지점에서 장면의 나머지 부분으로 반사된 후 센서로 반사됩니다. 이 빛, 즉 이중 반사 빛은 장면 깊이와 레이저에 의해 생성된 그림자의 존재에 대한 정보를 포함하고 있습니다. 우리의 실험 설정은 섹션 3.1에서 자세히 설명됩니다. 여러 조명 지점의 비행 시간 측정을 사용하여, 우리는 NeRF를 훈련시켜 이중 반사 빛의 비행 시간을 모델링합니다. 이중 반사 빛의 존재 여부는 그림자를 나타내어 가려진 기하학을 추론할 수 있게 하며, 그 비행 시간은 깊이를 나타냅니다. 우리의 방법은 기존의 단일 뷰 NeRF 또는 라이다 방법보다 더 높은 정확도로 3D 기하학을 재구성할 수 있습니다. 또한, 라이다를 사용함으로써 우리의 방법은 주변 조명이 밝고 장면 반사율이 낮은 상황에서도 작동할 수 있습니다. 우리는 또한 우리의 방법이 기존 라이다 방법보다 낮은 공간 및 시간 해상도에 더 잘 일반화됨을 보여줍니다.
요약하자면, 우리의 기여는 다음과 같습니다:
- 이중 반사 라이다 NeRF 모델: 우리는 이중 반사 빛 경로를 모델링하고 라이다 일시적 데이터를 사용하여 NeRF를 감독하는 방법을 제안합니다.
- 단일 뷰 3D 재구성: 우리의 방법이 장면의 세부 사항을 상상하지 않고 단일 뷰에서 장면을 정확하게 재구성할 수 있음을 입증합니다.
- 분석: 우리의 방법이 주변 조명, 장면 반사율 및 공간 및 시간 해상도에 대한 견고성을 연구합니다. 우리는 단일-광자 라이다로 캡처한 시뮬레이션된 장면의 데이터 세트를 준비합니다. 우리는 이 데이터를 사용하여 우리의 방법과 기존 방법을 평가합니다. 이러한 데이터를 시뮬레이션하는 것은 도메인 전문 지식이 필요합니다. 단일-광자 라이다를 사용한 머신 러닝에 대한 진입 장벽을 낮추고 이 방향에서의 향후 연구를 촉진하기 위해, 우리는 이 데이터 세트와 코드 및 모델 체크포인트를 프로젝트 페이지에 공개했습니다: PlatoNeRF.
연구 범위: 우리의 연구는 램버시안 장면의 재구성에 중점을 두며, 비램버시안 장면은 향후 연구로 남겨둡니다. 또한, 우리는 빛이 여러 표면에 반사되는 실내 장면에 집중합니다. 우리는 플래시 조명이 아닌 레이저 스캐닝을 가정합니다.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------
NeRF (Neural Radiance Fields)
NeRF(뉴럴 방사 필드)는 3D 장면을 표현하기 위해 사용되는 딥러닝 모델입니다. NeRF는 특정 장면에 대한 다수의 2D 이미지 데이터를 사용하여 3D 장면을 재구성합니다. 이 모델은 특정 지점에서 방사되는 빛의 양과 방향을 예측하는 방사 필드를 학습합니다.
NeRF의 주요 아이디어는 다음과 같습니다:
- 신경 네트워크 활용: NeRF는 신경 네트워크를 사용하여 입력 이미지에서 각 지점의 색상과 밀도를 예측합니다. 이 네트워크는 다양한 각도에서 찍은 2D 이미지들을 입력으로 받아들입니다.
- 방사 필드 학습: 신경 네트워크는 주어진 3D 공간에서 방사 필드를 학습합니다. 이는 공간의 각 점에서 특정 방향으로 방출되는 빛의 양과 색상을 나타내며, 이를 통해 3D 장면을 복원할 수 있습니다.
- 볼륨 렌더링: NeRF는 방사 필드를 사용하여 볼륨 렌더링을 수행합니다. 이는 3D 장면을 통과하는 광선을 따라 각 지점의 방사 데이터를 통합하여 최종 이미지를 생성하는 과정입니다.
- 다중 뷰 합성: NeRF는 여러 뷰의 이미지를 입력으로 사용하여 3D 공간을 완전히 재구성할 수 있습니다. 이는 다중 뷰 데이터의 방사 필드를 조합하여 임의의 새로운 뷰를 생성할 수 있게 합니다.
단일-광자 라이다의 이중 반사
단일-광자 라이다(Single-Photon Lidar)는 매우 민감한 광 검출기인 단일-광자 에벌랜치 다이오드(SPAD)를 사용하여 빛의 비행 시간을 측정하는 라이다 시스템입니다. 이 시스템은 매우 낮은 광량에서도 작동할 수 있으며, 고해상도 깊이 정보를 제공합니다.
이중 반사(Two-Bounce) 개념은 다음과 같습니다:
- 이중 반사 빛 경로: 전통적인 라이다 시스템은 장면에서 직접 반사된 첫 번째 반사 빛만을 사용하여 깊이를 측정합니다. 그러나 이중 반사 라이다는 빛이 두 번 반사된 후 센서에 도달하는 시간을 측정합니다. 이는 첫 번째 반사에서 가려진 물체의 정보를 제공할 수 있습니다.
- 깊이 정보 확장: 이중 반사 시간을 측정함으로써, 라이다 시스템은 단일 뷰에서 직접 볼 수 없는 가려진 영역의 깊이 정보를 추론할 수 있습니다. 이는 물리적으로 정확한 3D 재구성을 가능하게 합니다.
- 응용 예: 이중 반사 라이다는 주변 조명이 밝거나 반사율이 낮은 배경에서도 작동할 수 있어, 그림자에 의존하는 기존 방법보다 더 견고합니다.
이중 반사와 이중 슬릿 실험의 차이
이중 반사(Two-Bounce) 라이다와 이중 슬릿(Double-Slit) 실험은 서로 다른 물리적 현상을 다루고 있습니다.
- 이중 슬릿 실험: 이 실험은 파동-입자 이중성(Wave-Particle Duality)과 양자 물리학의 기본 원리를 보여줍니다. 빛이나 전자와 같은 입자가 두 개의 좁은 슬릿을 통과할 때, 파동 간섭 패턴이 형성되는 현상을 관찰합니다. 이 실험은 양자 상태의 중첩과 관측의 역할에 대한 중요한 통찰을 제공합니다.
- 이중 반사 라이다: 이는 빛이 장면에서 두 번 반사되어 센서에 도달하는 시간을 측정하여 가려진 기하학 정보를 복원하는 기술입니다. 이중 슬릿 실험과는 달리, 이중 반사 라이다는 주로 깊이 측정과 3D 재구성에 사용됩니다.
따라서, 단일-광자 라이다의 이중 반사는 이중 슬릿 실험의 연장선상에 있는 개념이 아니라, 3D 재구성을 위한 깊이 측정 기술 중 하나입니다.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------
2. 관련 연구
단일 뷰 재구성
단일 뷰 재구성은 제약 조건이 부족하여 잘못된 문제로 간주됩니다. 이를 해결하기 위해 데이터 기반 방법들은 학습된 2D 또는 3D 사전 지식을 사용하여 보이지 않는 영역을 상상합니다. 최근에는 생성에서의 확산 모델의 성공에 영감을 받아, 사전 학습된 2D 텍스트-이미지 모델에서 3D 대응을 추출하는 여러 방법이 연구되고 있습니다. 다른 방법들은 입력 뷰에 조건화된 다중 뷰 일관성 출력을 생성하기 위해 3D 사전 지식을 학습합니다. 이러한 방법들은 현실적인 이미지를 생성할 수 있지만, 기하학적 단서 없이 가려진 영역의 물리적으로 정확한 재구성을 보장할 수는 없습니다. 이는 우리의 연구 초점입니다.
그림자를 통한 신경 형태 추론
그림자를 통한 형태 추론(SfS)은 그림자가 투사하는 방식에 기반하여 가려진 기하학을 물리적으로 정확하게 추론하는 방법입니다. 전통적인 방법들은 그림자도, 공간 조각, 확률적 방법을 사용하여 SfS를 추론합니다. 최근 몇 년간, NeRF는 SfS를 학습하는 효과적인 표현으로 입증되었습니다. 이러한 방법들은 볼륨 렌더링을 활용하여 그림자가 있는 픽셀이 그림자 지점과 광원 사이의 기하학에서 비롯된다는 관찰을 기반으로 물체나 장면을 재구성합니다. 그러나 이러한 방법들은 주변 조명이나 낮은 반사율 배경으로 인해 그림자가 보이지 않게 되면 성능이 저하됩니다. 반면, 우리의 방법은 여전히 그림자에 의존하여 가려진 영역을 재구성하지만, RGB 센서가 아닌 라이다를 사용하기 때문에 이러한 영향에 더 견고합니다.
단일-광자 라이다를 사용한 3D 재구성
단일-광자 라이다는 시간 상관된 광도 측정을 기록하며 3D 재구성에 널리 사용됩니다. 우리의 연구에서는 가장 일반적인 단일-광자 에벌랜치 다이오드(SPAD)를 고려합니다. SPAD 기반 방법은 주로 장면을 능동적으로 조명하고 센서에 도달하는 광자의 수를 시간에 따라 기록하여 장면 기하학을 추론합니다. 가시광선 또는 비가시광선(예: 근적외선)의 파장을 방출하고 감지할 수 있습니다. 장면에서 각 광 반사는 장면의 기하학에 대한 정보를 제공합니다. 첫 번째 반사 빛은 장면의 깊이를 인코딩하며, 세 번째 반사 빛은 센서의 시야 밖에 있는 물체의 기하학에 대한 부분 정보를 인코딩합니다. NeRF는 라이다/ToF에서 첫 번째 및 세 번째 반사 빛을 활용하는 데 사용되었습니다. 우리는 최근 가려진 물체의 기하학을 인코딩하는 것으로 나타난 이중 반사 비행 시간에 중점을 둡니다. Henley et al.은 먼저 이중 반사 수신으로부터 장면 깊이를 추정하고, 그 다음으로 이중 반사 수신의 존재 여부로부터 추론된 그림자를 기반으로 가려진 기하학을 추정하는 두 단계 접근 방식을 제안했습니다. 이 연구에 영감을 받아, 우리는 NeRF를 사용하여 두 속성을 모두 재구성하는 단일 통합 파이프라인을 제안합니다. 우리의 연구는 다음과 같은 세 가지 주요 이점을 제공합니다: (1) 가시 및 숨겨진 기하학을 위한 통합 접근법, (2) 더 부드러운 장면 재구성, (3) 소비자 기기의 주요 제한 사항인 더 낮은 공간(예: 32×32) 및 시간 해상도 체제에 대한 더 나은 일반화.
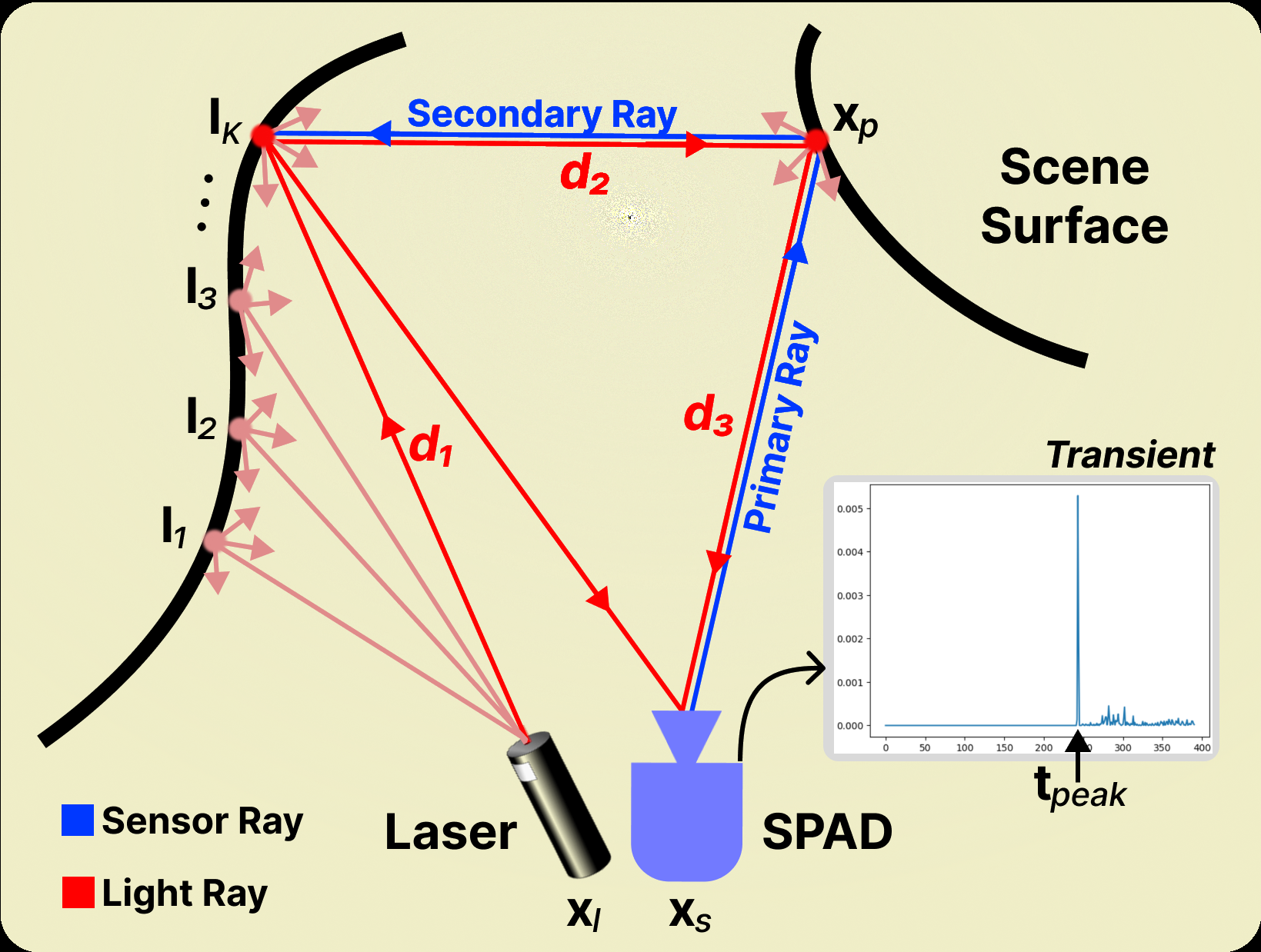
Figure 2

3. 단일 뷰 이중 반사 라이다를 사용한 NeRF
이 섹션에서는 NeRF를 사용하여 이중 반사 일시적 측정값으로부터 3D 기하학을 추출하는 방법을 설명합니다.
- 3.1 섹션에서는 실험 설정, 이미지 형성 모델 및 이중 반사 일시적 현상을 설명합니다.
- 3.2 섹션에서는 이중 반사 일시적 현상을 이용하여 NeRF를 훈련하는 방법을 설명합니다.
- 3.3 섹션에서는 우리의 방법과 결과를 재현할 수 있는 구현 세부 사항을 제공합니다.
3.1. 기호 및 문제 정의
실험 설정:

단일 반사 vs. 이중 반사 빛
SPAD 센서는 장면과 상호작용한 빛을 측정하여 장면의 속성을 추론할 수 있습니다. 이 문제에서 우리는 단일 반사 빛과 이중 반사 빛으로부터 3D 장면 기하학을 추론하는 것에 관심이 있습니다. 여기서 "반사"는 장면 표면에서 빛이 반사되는 횟수를 나타냅니다.

일시적 측정

그림자 측정

문제 정의
결과적으로 생성된 일시적 측정값에는 단일 반사 신호, 이중 반사 신호 및 그림자에 대한 정보가 포함됩니다. 단일 반사 및 이중 반사 신호는 센서에 보이는 물체에 대한 정보를 제공하며, 그림자는 장면의 가려진 부분에 대한 정보를 제공합니다. 이러한 측정값을 사용하여, 우리는 장면의 가시 및 가려진 부분의 3D 기하학을 재구성할 것입니다.
여기서 주의할 점은 비록 우리가 N개의 측정을 캡처하지만, 측정은 모두 동일한 뷰에서 레이저만 스캔하여 캡처된다는 것입니다.
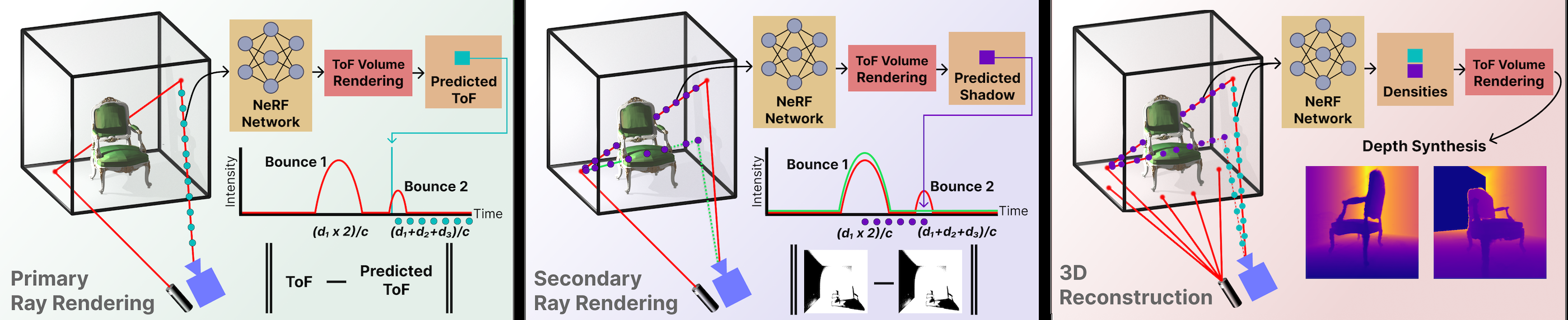
그림 3. 방법. PlatoNeRF는 NeRF로 모델링된 단일 뷰 투바운스 라이더 비행 시간으로부터 3D 장면 지오메트리를 학습합니다. 이 방법은 세 단계로 구성됩니다. (a) 먼저 카메라에서 장면으로 1차 광선을 렌더링합니다(3.2.1절). (b) 둘째, 가상 광선(광선이 장면에 처음 닿는 지점)으로 산란되어 이동하는 광선을 모델링합니다(3.2.2절). 두 단계 모두 단일 광자 라이더로 측정한 과도 현상을 통해 감독합니다. (c) 셋째, 2바운스 비행 시간을 재구성하면 3D 재구성이 가능하다는 것을 발견했습니다(3.2.3절).
3.2 이중 반사 볼륨 라이다 렌더링

3.2.1 1차 광선 렌더링

3.2.2 2차 광선 렌더링

3.2.3 일시적 측정 합성

그림자 손실

결합 손실 함수

3.3 구현 세부 사항
데이터 전처리
우리의 방법은 각 픽셀에 대해 다섯 가지 입력이 필요합니다:

비행 시간 계산

훈련

구현

-----------------------------------------------------------------------------------------------------------------------------------------------------------------
3.2.1 1차 광선 렌더링의 깊이 계산식 상세 전개




3.2.2 2차 광선 렌더링의 상세 전개




3.2.3 일시적 측정 합성의 상세 전개





결론
이러한 식과 과정을 통해 NeRF 모델은 단일 뷰에서 정확한 3D 기하학을 재구성할 수 있으며, 이를 통해 가시 및 가려진 영역의 깊이 정보를 동시에 얻을 수 있습니다.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------
4. 실험
우리는 여러 장면에 걸쳐 3D 재구성 작업에 대해 우리의 방법을 검증합니다. 먼저, 단일-광자 라이다를 위한 학습 기반 방법의 미래 작업을 가속화하기 위해 제공하는 시뮬레이션 데이터셋을 소개합니다. 그런 다음, 공간 및 시간 해상도, 주변 조명, 낮은 반사율 배경, 비평면 배경 및 조명 포인트 수에 대한 결과, 비교 및 소거 실험을 공유합니다.

그림 4. 정성적 깊이 결과: 저희는 기차 및 새로운 테스트 뷰 모두에서 예측 깊이에 대한 정성적 결과를 제공하며, 네 가지 장면에서 저희 방법, BF Lidar [7], S3-NeRF [44]를 기준 실측과 비교합니다. 각 방법은 표시된 하나의 열차 뷰에서 학습되어 전체 장면을 재구성합니다.
4.1 데이터셋
우리는 네 개의 시뮬레이션 데이터셋과 실제 데이터셋에서 우리의 방법을 검증합니다. 각 데이터셋은 아래에 설명되어 있습니다.
시뮬레이션 데이터셋: 우리는 네 개의 장면(의자, 토끼, 용, 의자 뒤에 가려진 토끼)을 포함하는 방의 데이터셋을 생성합니다. 이는 그림 4에 나타나 있습니다. 각 장면은 Pediredla et al.이 만든 Mitsuba의 시간 비행 확장을 사용하여 캡처됩니다. 각 장면에 대해, 우리는 왼쪽과 오른쪽 벽에 해당하는 장면의 왼쪽 및 오른쪽 부분에서 N=16개의 포인트를 조명하기 위해 휴리스틱하게 선택합니다. 각 조명 포인트에서 일시적 이미지를 기록합니다. 우리의 장면은 128 ps (3.84 cm)의 시간 해상도를 가진 512×512 SPAD를 사용하여 측정됩니다. 각 조명 포인트에 대해 0.05 μs (15 m)의 강도를 측정하여 픽셀당 391개의 타이밍 빈을 얻습니다. 또한, 우리는 훈련 뷰와 장면 주위의 120개의 테스트 뷰에서 평가를 위한 대응되는 실제 깊이 이미지를 렌더링합니다. 일시적 데이터, 깊이, 모든 센서 및 조명 매개변수는 공개될 예정입니다.

그림 5. 실제 결과. (a) 캡처된 장면(별은 조명 지점), (b) BF 라이더 결과, (c) PlatoNeRF 결과. 우리의 방법은 아티팩트/홀이 훨씬 적으면서도 BF 라이다와 유사한 결과를 산출합니다.
실제 데이터셋
우리는 시뮬레이션 외부에서 우리의 방법을 검증하기 위해 Henley et al. [7]이 캡처한 단일-광자 라이다 데이터를 사용합니다. 이 데이터셋은 그림 5에 나타난 단순한 실내 장면을 포함하고 있으며, 마네킹과 상자가 포함되어 있습니다. 이 장면은 200×200 픽셀 센서로 캡처되었으며, 계측 응답 함수는 128 ps(반치폭)입니다. 이 장면은 16개의 레이저 점으로 조명되었으며, 각 레이저 점에 대해 픽셀당 일시적 데이터가 캡처되었습니다.

표 1. 깊이 평가. PlatoNeRF를 라이더 및 RGB 기반 단일 뷰 3D 재구성 방법인 BF 라이더 [7] 및 S3-NeRF [44]와 각각 비교합니다. 기차 뷰와 120개의 새로운 테스트 뷰 모두에 대해 깊이 메트릭이 보고됩니다(L1의 경우 m 단위, PSNR의 경우 dB 단위).
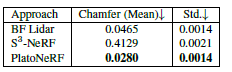
표 2. 포인트 클라우드 평가. 각 방법으로 생성된 포인트 클라우드 사이의 모따기 거리를 계산합니다. 메트릭은 시뮬레이션된 네 가지 장면 모두에 대해 평균을 구하고 표준편차를 보고합니다.
4.2 결과
비교 기준
우리는 우리의 방법을 두 가지 방법과 비교합니다. 하나는 학습 없이 단일 뷰 3D 재구성을 위해 이중 반사 라이다를 사용하는 방법이고, 다른 하나는 그림자를 측정한 RGB 카메라를 사용하여 NeRF를 훈련시키는 방법입니다. 현재까지 우리가 알기로는, 우리는 처음으로 이중 반사 라이다를 NeRF와 모델링하였으므로 이 작업에 대한 직접적인 비교는 없습니다.
- Bounce-Flash Lidar:
- 우리의 연구는 Bounce-Flash (BF) Lidar [7]에서 영감을 받았습니다. 이 방법은 기하학적 제약 조건과 그림자 조각화를 사용하여 단일 뷰에서 가시 깊이와 가려진 기하학을 추정하기 위해 이중 반사 라이다를 분석적으로 모델링합니다.
- BF Lidar의 출력은 가시 기하학을 위한 하나의 점 구름(PC)과 가려진 기하학을 위한 하나의 점 구름입니다. 우리는 비교를 위해 이 두 점 구름을 결합합니다.
- S3-NeRF [44]:
- S3-NeRF는 그림자를 사용하여 신경 장면 표현을 학습하는 최신 방법입니다. 다양한 조명 하에서 캡처된 단일 뷰 RGB 이미지를 사용하여 그림자와 음영 정보를 활용하여 신경 SDF 모델을 훈련시킵니다.
- 물체가 위치할 것으로 예상되는 원점에 구를 초기화하고, 알려진 카메라와 조명 위치를 사용하여 장면의 양방향 반사 분포 함수를 모델링합니다.
- S3-NeRF는 그림자를 드리우는 물체와 모든 배경 장면 기하학을 모두 재구성하여 적절한 비교 대상이 됩니다.
평가 기준
우리는 과거 연구에서와 같이 [14, 19, 44] 3D 재구성을 평가하기 위해 L1 깊이 오차를 사용합니다. 추가로, 재구성된 깊이 이미지에 대해 PSNR(피크 신호 대 잡음비)을 보고합니다. BF Lidar는 점 구름(PC)을 재구성하므로, Chamfer 거리 측정도 포함합니다. 깊이 측정을 위해 BF Lidar 점 구름을 깊이로 변환하려면 각 점의 크기를 증가시키고 깊이를 테스트 뷰로 투사하여 각 광선에 따라 가장 작은 깊이 값을 취합니다. 이는 깊이를 렌더링하기 전에 메쉬로 변환하는 것보다 더 나은 결과를 생성하는 것으로 나타났습니다.
시뮬레이션 결과
우리의 방법과 기준 방법들에 대한 훈련 및 120개의 테스트 뷰에 대한 깊이 측정값은 표 1에, Chamfer 거리는 표 2에 보고되었습니다. 우리의 방법은 두 가지 평가 기준 모두에서 BF Lidar와 S3-NeRF를 일관되게 능가하는 것으로 나타났습니다. 정성적인 결과는 그림 4에 나타나 있습니다. 우리의 방법은 장면의 가시 및 가려진 부분을 재구성하여 정확한 규모와 절대 깊이를 제공합니다. 암시적 표현을 사용하여 BF Lidar보다 훨씬 부드러운 결과를 달성합니다. 그러나 우리의 방법은 vanilla NeRF를 사용하기 때문에 일부 결과에서 작은 떠다니는 객체가 보일 수 있습니다. 반면, S3-NeRF는 SDF 표현을 사용하여 떠다니는 객체를 줄이지만, 과도하게 부드러운 결과를 초래합니다. 예를 들어, 용의 머리가 과도하게 부드럽게 표현되었습니다.
결과 분석
물체 바로 뒤에 있는 영역의 조명 포인트에 대해 이중 반사 신호가 없더라도, PlatoNeRF와 S3-NeRF는 이 영역에서 보간을 수행합니다. 반면, BF Lidar는 학습 기반이 아니므로 이 영역에서 이중 반사 신호의 부족으로 인해 구멍이 생깁니다. 우리는 이 영역을 깊이 측정에 포함하지 않습니다. 또한 PlatoNeRF는 카메라 시야각을 넘어 장면의 카메라에 가까운 부분까지 정확하게 외삽합니다. 마지막으로, S3-NeRF와 같은 RGB 기반 그림자 형태 추출 방법은 상대적 깊이를 생성하므로, S3-NeRF의 비투사 깊이 맵에 대해 반복적인 최근접 점(Iterative Closest Point) 방법을 실행해 보았지만, S3-NeRF의 지표를 개선하지 못했습니다. 원래 연구와 마찬가지로, 우리는 단일 반사로 렌더링된 RGB 이미지로 S3-NeRF를 훈련시키는데, 이는 다중 반사로 렌더링된 이미지로 훈련할 때 수렴하지 않음을 발견했기 때문입니다.
실제 세계 결과
그림 5에 실제 세계 결과를 보여주고 BF Lidar와 비교합니다. PlatoNeRF 방법은 경쟁력 있는 성능을 달성합니다. BF Lidar는 특히 가장자리와 마네킹의 반사 영역 근처에서 많은 인공물과 구멍을 생성하는 반면, PlatoNeRF는 반사 표면을 모델링하지 않음에도 불구하고 훨씬 적은 인공물과 구멍을 생성합니다. 일반적으로, PlatoNeRF는 더 부드러운 깊이를 생성하지만, 작은 떠다니는 물체가 눈에 띄며, 특히 가까운 바닥 영역에서 미래 작업의 대상이 될 수 있습니다.
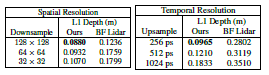
표 3. 라이다 센서의 절제. 소비자용 디바이스의 라이다는 연구용 라이다보다 공간 및 시간 해상도가 낮습니다. 이러한 센서 매개변수가 방법과 BF 라이다에 미치는 영향을 제거한 결과, 암시적 표현의 보간으로 인해 방법이 훨씬 더 일반화될 수 있음을 확인했습니다.

표 4. 씬 프로퍼티에 대한 제거. 그림자를 활용하는 RGB 메서드는 그림자의 가시성에 영향을 주는 씬 속성, 특히 주변광과 배경 알베도에 민감하다는 것을 관찰했습니다. 이러한 속성을 변화시키면서 S3-NeRF를 사용한 방법을 제거했으며, S3-NeRF는 비교적 견고하지만 라이더 센서를 사용하기 때문에 PlatoNeRF가 훨씬 더 강력하다는 점에 주목했습니다.
4.3 소거 실험 (Ablations)
우리는 다음 항목들이 우리의 방법에 어떻게 영향을 미치는지 이해하기 위해 소거 실험을 수행했습니다:
- 공간 및 시간 해상도 감소
- 주변 조명
- 배경 반사율
- 비평면 표면
- 조명 포인트 수
- 그림자 마스크 임계값
1번은 BF Lidar와 비교하여 우리의 방법이 관련 라이다 작업보다 더 나은 이점을 제공함을 강조합니다. 2번과 3번은 그림자 측정 시 RGB를 사용할 때의 근본적인 이점을 강조하기 위해 S3-NeRF와 비교됩니다. 마지막으로, 4번, 5번, 6번은 PlatoNeRF에 대해서만 수행됩니다. 모든 소거 실험은 의자 장면에서 수행되었습니다.
4.3.1 공간 및 시간 해상도
소비자 기기의 라이다는 연구용 라이다에 비해 공간 및 시간 해상도가 낮습니다. 우리는 PlatoNeRF가 BF Lidar에 비해 낮은 해상도 환경에서도 더 나은 일반화 성능을 제공하는 이점을 강조합니다. 이는 우리의 암시적 표현 방식 덕분입니다. 정량적 및 정성적 결과는 각각 표 3과 그림 6 (1-2번째 행)에 나타나 있습니다.

그림 6. 절제. 공간 및 시간 해상도가 PlatoNeRF에 미치는 영향을 연구한 결과, 두 가지 모두 크게 저하되었음에도 불구하고 장면이 잘 재구성되는 것을 확인했습니다. 시간적 해상도에 따라 깊이는 시각적으로 비슷하지만, 오류 맵은 의자의 변위가 증가하는 것을 나타냅니다. 마지막 행은 평면이 아닌 벽, 주변광, 조명 포인트 수가 적은 경우의 결과를 보여줍니다.
세부 해석
1. 공간 및 시간 해상도 감소
- 비교 대상: BF Lidar와 비교하여 우리의 방법인 PlatoNeRF의 장점을 평가합니다.
- 결과: PlatoNeRF는 낮은 해상도 환경에서도 더 나은 성능을 보입니다. 이는 암시적 표현 방식 덕분에 가능한 것으로, BF Lidar에 비해 더 부드럽고 정확한 3D 재구성을 제공합니다.
- 정량적 결과: 표 3에서 확인할 수 있습니다.
- 정성적 결과: 그림 6의 1-2번째 행에서 확인할 수 있습니다.
2. 주변 조명
- 비교 대상: S3-NeRF와 비교하여 라이다 사용의 이점을 평가합니다.
- 결과: 라이다는 주변 조명의 영향을 덜 받기 때문에, PlatoNeRF는 더 정확한 그림자 및 깊이 정보를 제공합니다.
3. 배경 반사율
- 비교 대상: S3-NeRF와 비교하여 라이다 사용의 이점을 평가합니다.
- 결과: 라이다는 배경 반사율이 낮은 경우에도 정확한 측정을 제공하므로, PlatoNeRF는 더 일관된 결과를 제공합니다.
4. 비평면 표면
- 비교 대상: PlatoNeRF 단독 실험.
- 결과: PlatoNeRF는 비평면 표면에서도 높은 정확도를 유지합니다.
5. 조명 포인트 수
- 비교 대상: PlatoNeRF 단독 실험.
- 결과: 조명 포인트 수가 증가할수록 재구성의 정확도가 향상됩니다.
6. 그림자 마스크 임계값
- 비교 대상: PlatoNeRF 단독 실험.
- 결과: 그림자 마스크 임계값을 조정하여 재구성의 정확도와 부드러움을 최적화할 수 있습니다.
공간 해상도
공간 해상도를 연구하기 위해, 시야각은 동일하게 유지하면서 픽셀 수를 4배, 8배, 16배로 다운샘플링했습니다. 결과적으로 공간 해상도는 각각 128×128, 64×64, 32×32가 되었습니다. 우리는 BF Lidar의 정확도가 PlatoNeRF보다 더 크게 저하된다는 것을 발견했습니다. 이는 BF Lidar에는 누락된 픽셀을 보간할 메커니즘이 없기 때문입니다. 심지어 32×32 해상도에서도, PlatoNeRF는 장면을 정확하게 재구성하지만 약간 더 많은 인공물이 발생합니다. 자세한 내용은 부록에서 확인할 수 있습니다.
시간 해상도
일시적 데이터의 빈 크기를 128 ps에서 256 ps, 512 ps, 1024 ps로 증가시키면서 각 빈 내의 강도를 통합하여 일시적 데이터의 빈 수를 줄였습니다. 이는 깊이 정보의 정밀도를 감소시킵니다. 우리는 BF Lidar의 깊이 오차가 PlatoNeRF보다 더 많이 감소한다는 것을 발견했습니다. BF Lidar가 예측한 표면은 픽셀당 깊이의 모호성 때문에 거칠고 불규칙해집니다(부록 참조). 반면, PlatoNeRF는 빈 크기가 증가함에 따라 예측된 깊이가 덜 정확해지지만, 부드러운 기하학과 인접한 픽셀 간의 일관성을 유지합니다.
4.3.2 주변 조명 및 낮은 반사율 배경
개요
실제 환경에서는 높은 주변 조명이나 낮은 장면 반사율이 있을 수 있습니다. 이는 RGB 이미지에서 그림자를 감지하는 것을 어렵게 만듭니다. 반면, PlatoNeRF와 같은 라이다 기반 방법은 근본적으로 낮은 신호 대 잡음 비율(SNR)과 신호 대 배경 비율(SBR) 시나리오에서 더 견고합니다. 주변 조명과 낮은 반사율은 RGB와 라이다 기반 접근 방식 모두에 영향을 미치지만, 라이다 기반 접근 방식은 시간 및 파장 게이팅을 통해 영향을 완화할 수 있습니다.
시간 게이팅(Time Gating)
- 주변 소음은 시간에 따라 균일하게 분포합니다.
- 시간 게이팅은 펄스 신호가 포함된 타이밍 빈만 고려하여 주변 소음을 억제합니다.
파장 게이팅(Wavelength Gating)
- 파장 게이팅은 SPAD 센서가 측정하지 않는 파장의 주변 소음을 억제합니다.
- 반면, RGB 센서는 가시 파장에 대한 광대역 감도를 가집니다.
이 게이팅 원리에 대한 자세한 설명은 부록에 제공됩니다. 이러한 소거 실험에 대한 정량적 결과는 표 4에 보고됩니다.
주변 조명
주변 조명이 증가하면 SBR 또는 SNR 항목의 배경과 소음이 증가합니다. 우리는 PlatoNeRF가 장면의 주변 조명을 처리할 수 있음을 실험적으로 검증했으며, S3-NeRF의 깊이 오차는 증가합니다. 이 실험을 위해, 두 방법을 훈련시키기 위해 추가된 영역 조명으로 장면을 렌더링합니다. 영역 조명의 강도는 RGB와 라이다 렌더링 모두에서 동일합니다. 실내에서는 포화 또는 누적 왜곡(pileup distortion) 효과가 중요하지 않으므로 모델링하지 않았습니다. 주변 조명 하에서 PlatoNeRF의 재구성은 그림 6 (3번째 행)에, S3-NeRF의 결과는 부록에 나타나 있습니다.
반사율
반사율을 줄이면 SNR 및 SBR 항목에서 신호가 감소합니다. 그러나 RGB 센서와 달리, 반사율은 라이다에 미치는 영향이 적습니다. PlatoNeRF와 S3-NeRF에 대한 영향을 보여주기 위해 모든 배경 표면의 반사율을 줄였습니다. 그림자가 육안으로는 여전히 식별 가능하지만(부록 참조), 낮은 반사율은 S3-NeRF의 깊이 오차를 증가시키는 반면, PlatoNeRF에는 영향을 미치지 않습니다. S3-NeRF는 훈련 뷰에서 정확한 깊이를 생성하지만, 그림자가 약해지면서 가려진 영역의 기하학이 누락됩니다.
4.3.3 기타 소거 실험
마지막으로 우리는 PlatoNeRF에서 (a) 비평면 배경 기하학, (b) 조명 지점 수, (c) 그림자 마스크 임계값이 미치는 영향을 연구했습니다. 각 항목에 대한 추가 결과는 부록에 제공됩니다. (a)와 (b)에 대한 정성적 결과는 그림 6 (3번째 행)에 나타나 있습니다.
(a) 비평면 배경 기하학
비평면 장면에는 곡선형 배경 벽이 포함되어 있습니다. 테스트 뷰 전반에서 PlatoNeRF의 깊이 L1 오차는 7.75 cm이고, PSNR은 27.25 dB로 이전 실험과 유사한 결과를 보였습니다.
(b) 조명 지점 수
조명 지점 수를 16개에서 8개로 줄인 경우, 테스트 뷰 전반에서 L1 오차는 9.12 cm, PSNR은 26.33 dB로, 16개 뷰를 모두 사용한 경우보다 약간 떨어졌습니다.
(c) 그림자 마스크 임계값
그림자 마스크 임계값을 0에서 1 사이로 조정한 결과, L1 오차는 6.88 cm에서 70 cm 사이로 변동하여, 그림자 마스크 임계값의 중요성을 강조했습니다.
이러한 실험을 통해 PlatoNeRF의 성능이 다양한 조건 하에서 어떻게 변화하는지를 파악할 수 있었습니다.
5. 결론
우리는 NeRF를 사용하여 라이다 측정을 재구성하는 방법을 제시합니다. 이 방법은 단일 뷰에서 물리적으로 정확한 3D 기하학을 학습할 수 있게 합니다. 우리는 펄스 레이저로 장면을 조명하고, 이중 반사 비행 시간을 기록합니다. 이 데이터를 사용하여 NeRF를 감독하며, NeRF는 이중 반사 빛의 광 경로를 학습하도록 훈련됩니다. 우리의 방법은 단일 뷰 3D 재구성에서 관련 연구를 능가하며, 완전히 가려진 물체가 있는 장면을 재구성하고, 어느 뷰에서도 메트릭 깊이를 학습합니다. 마지막으로, 우리는 다양한 센서 매개변수와 장면 속성에 대한 일반화를 입증합니다.
한계
우리의 방법에는 몇 가지 한계가 있습니다. 첫째, 우리는 램버시안 반사만을 모델링합니다. 둘째, 우리의 방법은 기본적으로 vanilla NeRF 위에 구축되어 있어 가끔 떠다니는 물체(floaters)가 발생할 수 있습니다. 그러나 우리의 방법은 NeRF의 변형에 구애받지 않으며, 미래에는 다른 변형에도 통합될 수 있습니다.
향후 연구
이 연구는 라이다가 보편화됨에 따라 유망한 방향이라고 생각합니다. PlatoNeRF가 가능하게 하는 향후 연구 방향에는 텍스처 기하학을 복원하기 위해 RGB와 라이다를 신경 렌더링과 통합하는 것, 단일 뷰 3D 재구성에 자주 사용되는 데이터 사전 지식을 사용하는 것, 비행 시간에서 모호성을 일으키는 반사 특성을 처리하는 것, 그리고 두 번 이상의 빛 반사를 모델링하는 것이 포함됩니다.
감사의 글
우리는 Akshat Dave에게 논문 피드백과 비행 시간 이미징에 대한 통찰을 제공해 주셔서 감사드리며, Wenqi Yang에게 S3-NeRF에 대한 지도에 감사드립니다.
입력: 위치 정보 (input_pts, 3차원), 시점 정보 (input_views, 3차원)
위치 정보 경로
┌───────────────────────────────────────────────────────────────┐
│ Linear(input_ch, W) │
│ │ │
│ ReLU │
│ │ │
│ (1부터 D-1까지 반복) │
│ │ │
│ if i in skips: │
│ Concatenate(input_pts, h) │
│ Linear(W + input_ch, W) │
│ else: │
│ Linear(W, W) │
│ │ │
│ ReLU │
└───────────────────────────────────────────────────────────────┘
시점 정보 경로 (use_viewdirs=True인 경우)
┌───────────────────────────────────────────────────────────────┐
│ Linear(W, W) (feature_linear) │
│ │ │
│ ReLU │
│ │ │
│ Concatenate(feature, input_views) │
│ Linear(input_ch_views + W, W//2) │
│ │ │
│ ReLU │
│ │ │
│ (1개의 추가 레이어로 확장 가능) │
│ │ │
│ if rgb_linear is not None: │
│ Linear(W//2, 3) or Linear(W//2, 1) (RGB 값 예측) │
│ Concatenate(rgb, alpha) │
│ else: │
│ RGB 값을 랜덤하게 초기화 │
└───────────────────────────────────────────────────────────────┘
출력
┌───────────────────────────────────────────────────────────────┐
│ Linear(W, output_ch) (use_viewdirs=False인 경우) │
│ (알파와 RGB 값 포함) │
└───────────────────────────────────────────────────────────────┘
출력: 위치의 색상 (RGB) 및 밀도 (alpha)'인공지능' 카테고리의 다른 글
| Relightable Gaussian Codec Avatars (1) | 2024.06.23 |
|---|---|
| Nymeria: A Massive Collection of Multimodal Egocentric Daily Motion in the Wild (2) | 2024.06.22 |
| Direct Preference Optimization: Your Language Model is Secretly a Reward Model (1) | 2024.06.22 |
| Nemotron-4 340B Technical Report (3) | 2024.06.20 |
| Mixture-of-Agents Enhances Large Language ModelCapabilities (1) | 2024.06.19 |



