Deep Residual Learning for Image Recognition

https://arxiv.org/abs/1512.03385

Deep Residual Learning for Image Recognition

 

요약:

더 깊은 신경망은 훈련하기가 더 어렵습니다. 우리는 이전에 사용된 것보다 훨씬 더 깊은 네트워크의 훈련을 용이하게 하기 위해 잔차 학습(residual learning) 프레임워크를 제시합니다. 우리는 층(layer)을 독립적인 함수로 학습하는 대신, 층 입력에 대한 잔차 함수를 학습하도록 명시적으로 재구성합니다. 이러한 잔차 네트워크가 최적화하기 더 쉽고 깊이가 증가함에 따라 정확도가 향상된다는 종합적인 실험적 증거를 제시합니다. ImageNet 데이터셋에서 우리는 VGG 네트워크보다 8배 깊지만 복잡도는 더 낮은 최대 152층의 잔차 네트워크를 평가했습니다. 이러한 잔차 네트워크 앙상블은 ImageNet 테스트 셋에서 3.57%의 오류율을 기록했으며, 이는 ILSVRC 2015 분류 과제에서 1위를 차지한 결과입니다. 또한 CIFAR-10 데이터셋에서 100층과 1000층에 대한 분석을 제시합니다.

 

표현의 깊이는 많은 시각적 인식 작업에서 매우 중요합니다. 순전히 우리가 사용한 매우 깊은 표현 덕분에 COCO 객체 탐지 데이터셋에서 28%의 상대적 성능 향상을 달성했습니다. 깊은 잔차 네트워크는 우리가 ILSVRC 및 COCO 2015 대회에 제출한 모델의 기반이 되었으며, 이 대회에서 ImageNet 탐지, ImageNet 위치 확인, COCO 탐지 및 COCO 분할 작업에서 1위를 차지했습니다.

 

Figure 1: CIFAR-10 데이터셋에서 20층과 56층의 "평범한" 네트워크에 대한 훈련 오류(왼쪽)와 테스트 오류(오른쪽)를 나타냅니다. 더 깊은 네트워크는 더 높은 훈련 오류를 가지며, 결과적으로 테스트 오류도 높아집니다. ImageNet에서 유사한 현상은 그림 4에 나타나 있습니다.

1. 서론

딥 컨볼루션 신경망(Convolutional Neural Networks, CNN)은 이미지 분류 분야에서 일련의 돌파구를 가져왔습니다. 딥 네트워크는 자연스럽게 저/중/고수준의 특징과 분류기를 종단간 멀티레이어 방식으로 통합하며, 이러한 특징의 '수준'은 쌓이는 층(깊이)의 수에 의해 강화될 수 있습니다. 최근의 증거들은 네트워크의 깊이가 매우 중요하다는 것을 보여주었으며, 이미지넷(ImageNet) 데이터셋에서 도출된 최상의 결과들은 모두 매우 깊은 모델을 사용하고 있습니다. 이 모델들은 깊이가 16층에서 30층까지에 이릅니다. 또한, 많은 다른 비시각적 인식 작업에서도 깊은 모델로부터 큰 혜택을 받았습니다.

이러한 깊이의 중요성에 의해, "더 나은 네트워크를 학습하는 것이 단순히 층을 더 쌓는 것만큼 쉬운가?"라는 질문이 제기됩니다. 이 질문에 답하는 데 있어 큰 장애물은 잘 알려진 기울기 소실 및 폭발 문제입니다. 이러한 문제는 학습 초기에 네트워크의 수렴을 방해하지만, 정규화된 초기화 방법과 중간 정규화 층을 사용함으로써 이 문제가 크게 해결되었습니다. 이로 인해 수십 층을 가진 네트워크가 확률적 경사 하강법(SGD)과 역전파 알고리즘을 통해 수렴을 시작할 수 있게 되었습니다.

 

그러나 더 깊은 네트워크가 수렴하기 시작할 때, '성능 저하 문제'가 노출되었습니다. 네트워크 깊이가 증가함에 따라 정확도가 포화되었다가(이는 예상할 수 있음) 급격히 떨어지는 현상이 발생합니다. 놀랍게도 이러한 성능 저하는 과적합 때문이 아니며, 적절한 깊이를 가진 모델에 층을 더 추가하면 훈련 오류가 더 높아집니다. 이러한 현상은 다른 연구들에서도 보고되었고, 우리의 실험에 의해 철저히 검증되었습니다. 그림 1은 이러한 전형적인 예시를 보여줍니다.

 

훈련 정확도의 저하 현상은 모든 시스템이 동일하게 최적화되기 쉽지 않다는 것을 나타냅니다. 더 얕은 아키텍처와 그에 더 많은 층을 추가한 더 깊은 아키텍처를 생각해 봅시다. 이 더 깊은 모델에는 구조적으로 해결책이 존재합니다. 추가된 층들은 항등 매핑(identity mapping)을 수행하고, 나머지 층들은 학습된 얕은 모델에서 복사해 오면 됩니다. 이 구성된 해결책의 존재는 더 깊은 모델이 더 얕은 모델보다 훈련 오류가 더 높아지지 않아야 함을 시사합니다. 그러나 실험 결과, 우리가 현재 사용하는 솔버(solvers)는 이 구성된 해결책만큼 좋거나 더 나은 해를 찾지 못하거나, 이를 찾는 데 실현 가능한 시간이 걸립니다.

 

이 논문에서 우리는 잔차 학습(residual learning) 프레임워크를 도입함으로써 이러한 성능 저하 문제를 해결합니다. 몇 개의 층이 직접 원하는 기본 매핑을 학습하는 대신, 우리는 이 층들이 잔차 매핑을 학습하도록 명시적으로 설정합니다. 공식적으로, 원하는 기본 매핑을 H(x)라고 할 때, 우리는 쌓인 비선형 층들이 다른 매핑인 F(x) := H(x) - x를 학습하도록 합니다. 이때 원래의 매핑은 F(x) + x로 재구성됩니다. 우리는 잔차 매핑을 최적화하는 것이 원래의, 참조되지 않은 매핑을 최적화하는 것보다 더 쉽다고 가정합니다. 극단적인 경우, 항등 매핑이 최적일 경우, 잔차를 0으로 만드는 것이 비선형 층의 스택을 통해 항등 매핑을 맞추는 것보다 더 쉬울 것이라고 추측합니다.

 

Figure 2: 잔차 학습의 빌딩 블록.

 

F(x) + x의 공식은 "단축 연결(shortcut connections)"을 사용한 피드포워드 신경망으로 구현될 수 있습니다(Fig. 2). 단축 연결은 하나 이상의 층을 건너뛰는 연결을 의미합니다. 우리의 경우, 단축 연결은 단순히 항등 매핑(identity mapping)을 수행하며, 그 출력은 쌓인 층의 출력에 더해집니다(Fig. 2). 항등 단축 연결은 추가적인 파라미터나 계산 복잡도를 증가시키지 않습니다. 전체 네트워크는 여전히 확률적 경사 하강법(SGD)과 역전파를 통해 종단 간 학습이 가능하며, 일반적인 라이브러리(Caffe 등)를 사용해 솔버를 수정하지 않고도 쉽게 구현할 수 있습니다.

 

우리는 ImageNet 데이터셋에서 성능 저하 문제를 보여주고, 우리의 방법을 평가하기 위한 종합적인 실험을 제시합니다. 실험 결과는 다음과 같습니다:

1. 우리의 매우 깊은 잔차 네트워크는 최적화하기 쉽지만, 단순히 층을 쌓은 "평범한" 네트워크는 깊이가 증가할수록 더 높은 훈련 오류를 보입니다.
2. 우리의 깊은 잔차 네트워크는 깊이가 크게 증가함에 따라 정확도 향상을 쉽게 누리며, 이전 네트워크보다 훨씬 뛰어난 결과를 산출합니다.

유사한 현상은 CIFAR-10 데이터셋에서도 나타나, 최적화의 어려움과 우리 방법의 효과가 특정 데이터셋에 국한되지 않음을 시사합니다. 우리는 이 데이터셋에서 100층이 넘는 모델을 성공적으로 훈련시켰으며, 1000층이 넘는 모델도 탐구했습니다.

 

ImageNet 분류 데이터셋에서 우리는 매우 깊은 잔차 네트워크를 통해 뛰어난 결과를 얻었습니다. 우리의 152층 잔차 네트워크는 ImageNet에서 발표된 가장 깊은 네트워크로, 여전히 VGG 네트워크보다 복잡도가 낮습니다. 우리의 앙상블은 ImageNet 테스트 셋에서 3.57%의 top-5 오류율을 기록하며 ILSVRC 2015 분류 대회에서 1위를 차지했습니다. 이러한 매우 깊은 표현은 다른 인식 작업에서도 우수한 일반화 성능을 보였으며, ImageNet 탐지, ImageNet 위치 확인, COCO 탐지, COCO 분할 작업에서도 1위를 차지하게 했습니다. 이는 잔차 학습 원리가 일반적임을 강력하게 증명하며, 우리는 이 원리가 다른 비전 및 비비전 문제에도 적용될 수 있을 것이라 기대합니다.

 

2. 관련 연구

잔차 표현(Residual Representations): 이미지 인식에서, VLAD[18]는 사전에 대한 잔차 벡터로 인코딩하는 표현 방식이며, Fisher Vector[30]는 VLAD의 확률적 버전으로 공식화될 수 있습니다[18]. 두 방식 모두 이미지 검색과 분류에서 강력한 얕은 표현 방식입니다[4, 48]. 벡터 양자화(Vector Quantization)에서, 잔차 벡터를 인코딩하는 것이 원래 벡터를 인코딩하는 것보다 더 효과적임이 입증되었습니다[17].

 

저수준 비전 및 컴퓨터 그래픽스에서는 편미분 방정식(PDE)을 해결하기 위해 널리 사용되는 다중격자(Multigrid) 방법[3]이 시스템을 다중 스케일에서 하위 문제로 재구성합니다. 각 하위 문제는 더 거친 스케일과 더 세밀한 스케일 간의 잔차 솔루션을 책임집니다. 다중격자의 대안으로는 계층적 기저 사전조건화(hierarchical basis preconditioning)[45, 46]가 있으며, 이는 두 스케일 간의 잔차 벡터를 나타내는 변수를 사용합니다. 이러한 솔버들은 잔차의 성격을 인식하지 못하는 표준 솔버들보다 훨씬 빠르게 수렴함이 입증되었습니다[3, 45, 46]. 이러한 방법들은 좋은 재구성 또는 사전조건화가 최적화를 단순화할 수 있음을 시사합니다.

 

단축 연결(Shortcut Connections): 단축 연결을 이끄는 실천 및 이론은 오랜 기간 동안 연구되어 왔습니다[2, 34, 49]. 초기 다층 퍼셉트론(MLP)을 훈련하는 방법 중 하나는 네트워크 입력과 출력을 연결하는 선형 층을 추가하는 것이었습니다[34, 49]. 또한 [44, 24]에서는 몇몇 중간 층이 소실/폭발하는 기울기 문제를 해결하기 위해 보조 분류기에 직접 연결되었습니다. [39, 38, 31, 47]의 논문들은 단축 연결을 통해 층 반응, 기울기, 역전파 오류를 중심으로 조정하는 방법을 제안했습니다. [44]에서는 "인셉션" 층이 단축 브랜치와 더 깊은 몇 개의 브랜치로 구성되었습니다.

 

우리의 연구와 동시에 "하이웨이 네트워크(highway networks)"[42, 43]는 게이팅 함수(gating functions)[15]를 가진 단축 연결을 제안했습니다. 이 게이트는 데이터에 의존하며 파라미터를 갖는 반면, 우리의 항등 단축 연결은 파라미터가 없습니다. 하이웨이 네트워크에서 게이팅 단축이 "닫히면"(0에 가까워질 때) 이 네트워크의 층들은 비잔차 함수(non-residual functions)를 나타냅니다. 반대로, 우리의 공식화는 항상 잔차 함수를 학습하며, 우리의 항등 단축 연결은 결코 닫히지 않고 모든 정보가 항상 전달되며 추가적인 잔차 함수를 학습해야 합니다. 또한, 하이웨이 네트워크는 매우 깊은 네트워크(예: 100층 이상)에서 정확도 향상을 보여주지 못했습니다.

3. 깊은 잔차 학습

3.1 잔차 학습

H(x)를 몇 개의 쌓인 층(필수적으로 전체 네트워크가 아님)에서 맞춰야 할 기본 매핑이라고 가정합시다. 여기서 x는 이러한 층의 첫 번째 입력을 나타냅니다. 여러 비선형 층이 복잡한 함수를 점근적으로 근사할 수 있다는 가정을 한다면, 동일하게 잔차 함수, 즉 H(x) - x를 근사할 수 있다고 가정할 수 있습니다(입력과 출력의 차원이 동일하다고 가정). 따라서 쌓인 층들이 H(x)를 근사하도록 기대하는 대신, 우리는 이 층들이 잔차 함수 F(x) := H(x) - x를 명시적으로 근사하도록 합니다. 그러면 원래의 함수는 F(x) + x로 변환됩니다. 두 형태 모두 원하는 함수를 점근적으로 근사할 수 있지만(가정에 따르면), 학습의 용이성은 다를 수 있습니다.

 

이러한 재구성은 성능 저하 문제와 관련된 직관에 반하는 현상(Fig. 1, 왼쪽)에서 동기를 얻었습니다. 서론에서 논의한 것처럼, 추가된 층들이 항등 매핑으로 구성될 수 있다면, 더 깊은 모델의 훈련 오류는 얕은 모델보다 더 크지 않아야 합니다. 그러나 성능 저하 문제는 솔버들이 여러 비선형 층을 통해 항등 매핑을 근사하는 데 어려움을 겪을 수 있음을 시사합니다. 잔차 학습의 재구성을 통해, 항등 매핑이 최적이라면 솔버는 여러 비선형 층의 가중치를 0으로 만들어 항등 매핑에 가까워질 수 있습니다.

 

실제 상황에서는 항등 매핑이 최적일 가능성은 낮지만, 우리의 재구성이 문제를 사전조건화(precondition)하는 데 도움이 될 수 있습니다. 만약 최적 함수가 0 매핑보다 항등 매핑에 더 가깝다면, 솔버가 항등 매핑을 기준으로 하는 작은 변화(perturbations)를 찾는 것이 새로운 함수를 학습하는 것보다 더 쉬울 것입니다. 우리는 실험(Fig. 7)을 통해 학습된 잔차 함수들이 일반적으로 작은 반응을 보인다는 것을 보여주며, 이는 항등 매핑이 합리적인 사전조건화를 제공함을 시사합니다.

 

3.2. 단축 연결을 통한 항등 매핑

우리는 잔차 학습을 여러 쌓인 층에 적용합니다. 하나의 빌딩 블록은 Fig. 2에 표시되어 있습니다. 공식적으로, 이 논문에서 우리는 다음과 같이 정의된 빌딩 블록을 고려합니다:

여기서 x와 y는 고려 중인 층들의 입력과 출력 벡터입니다. 함수 F(x;{W_i​})는 학습해야 하는 잔차 매핑을 나타냅니다. Fig. 2에 예시된 두 개의 층으로 구성된 경우, F=W_2​σ(W_1​x)이며, 여기서 σ는 ReLU 활성화 함수이고, 편의를 위해 편향(biases)은 생략되었습니다. F+x 연산은 단축 연결과 요소별 덧셈을 통해 수행됩니다. 우리는 덧셈 후 두 번째 비선형성(즉, σ(y))을 적용합니다(이 부분은 Fig. 2를 참조).

 

이 방정식에서의 단축 연결은 추가적인 파라미터나 계산 복잡도를 도입하지 않습니다. 이는 실용적으로 매력적일 뿐만 아니라 평범한 네트워크와 잔차 네트워크를 비교할 때도 중요합니다. 우리는 동일한 파라미터 수, 깊이, 너비, 계산 비용(요소별 덧셈은 무시할 수 있을 만큼 작음)을 가지는 평범한/잔차 네트워크를 공정하게 비교할 수 있습니다.

 

방정식 (1)에서 x와 F의 차원이 동일해야 합니다. 만약 차원이 일치하지 않는 경우(예: 입력/출력 채널이 변경될 때), 단축 연결을 통해 차원을 맞추기 위해 선형 사영 W_s를 수행할 수 있습니다:

 

 

또한, 방정식 (1)에서 W_s​를 정사각 행렬로 사용할 수도 있습니다. 그러나 실험을 통해 항등 매핑이 성능 저하 문제를 해결하기에 충분하며 경제적이라는 것을 보여주었으므로, 차원을 맞출 때만 W_s​를 사용합니다.

 

잔차 함수 F의 형식은 유연합니다. 이 논문의 실험에서는 두 개 또는 세 개의 층으로 구성된 함수 F를 사용했으며(Fig. 5), 더 많은 층도 가능합니다. 하지만 F가 단일 층만 가지고 있을 경우, 방정식 (1)은 선형 층과 유사해집니다: y = W_1 x + x, 여기서 우리는 특별한 이점을 관찰하지 못했습니다.

 

또한, 위의 표기법은 간단히 하기 위해 완전 연결 층에 대해 설명되었지만, 이는 합성곱 층에도 적용할 수 있습니다. 함수 F(x; {W_i})는 여러 합성곱 층을 나타낼 수 있으며, 요소별 덧셈은 두 개의 특징 맵(feature maps)에 대해 채널별로 수행됩니다

 

3.3. 네트워크 아키텍처

우리는 다양한 평범한/잔차 네트워크를 테스트했으며, 일관된 현상을 관찰했습니다. 논의를 위한 예시를 제공하기 위해, ImageNet에서 두 가지 모델을 설명합니다.

 

평범한 네트워크(Plain Network): 우리의 평범한 네트워크 기준선(Fig. 3, 가운데)은 주로 VGG 네트워크[41](Fig. 3, 왼쪽)의 철학에서 영감을 받았습니다. 합성곱 층은 주로 3x3 필터를 가지고 있으며, 두 가지 간단한 설계 규칙을 따릅니다: (i) 동일한 출력 피처 맵 크기에서는 층들이 동일한 수의 필터를 가지며, (ii) 피처 맵 크기가 절반으로 줄어들 경우, 계산 시간 복잡도를 층당 유지하기 위해 필터 수가 두 배가 됩니다. 우리는 다운샘플링을 스트라이드 2를 가진 합성곱 층으로 직접 수행합니다. 네트워크는 글로벌 평균 풀링층과 소프트맥스(softmax)를 가진 1000-유형 완전 연결층으로 끝납니다. 총 가중치가 있는 층의 수는 Fig. 3(가운데)에서 34개입니다.

 

주목할 점은 우리의 모델이 VGG 네트워크[41](Fig. 3, 왼쪽)보다 필터 수가 적고 복잡도가 낮다는 것입니다. 우리의 34층 기준선 모델은 36억 FLOPs(곱셈-덧셈 연산)를 가지며, 이는 VGG-19의 18%에 불과한 196억 FLOPs입니다.

 

Figure 3: ImageNet을 위한 예시 네트워크 아키텍처. 왼쪽: 참고용 VGG-19 모델(196억 FLOPs). 가운데: 34개의 파라미터 층을 가진 평범한 네트워크(36억 FLOPs). 오른쪽: 34개의 파라미터 층을 가진 잔차 네트워크(36억 FLOPs). 점선으로 표시된 단축 연결은 차원을 증가시킵니다. 표 1은 더 많은 세부 사항과 다른 변형들을 보여줍니다.

 

잔차 네트워크(Residual Network)

위에서 설명한 평범한 네트워크를 기반으로, 우리는 단축 연결을 삽입하여(Fig. 3, 오른쪽) 네트워크를 잔차 버전으로 변환합니다. 항등 단축 연결(Eqn.(1))은 입력과 출력의 차원이 동일할 때(실선 단축 연결, Fig. 3) 직접 사용할 수 있습니다. 차원이 증가할 때(점선 단축 연결, Fig. 3), 두 가지 옵션을 고려합니다: (A) 단축 연결은 여전히 항등 매핑을 수행하며, 차원을 증가시키기 위해 추가적인 0이 채워집니다. 이 옵션은 추가적인 파라미터를 도입하지 않습니다. (B) 차원을 맞추기 위해 Eqn.(2)의 사영 단축 연결이 사용됩니다(1x1 합성곱으로 수행). 두 가지 옵션 모두 단축 연결이 두 가지 크기의 피처 맵을 가로지르는 경우, 스트라이드 2를 사용하여 수행됩니다.

3.4. 구현

우리는 ImageNet에 대한 구현을 [21, 41]의 방식에 따라 진행합니다. 이미지는 [256; 480] 범위에서 짧은 변을 무작위로 샘플링하여 크기 조정(scale augmentation)됩니다[41]. 224x224 크기의 크롭(crop)이 이미지 또는 그 수평 뒤집기에서 무작위로 샘플링되며, 픽셀별 평균이 차감됩니다[21]. [21]에서 사용된 표준 색상 증강도 적용됩니다. 우리는 각 합성곱 후와 활성화 이전에 배치 정규화(BN)[16]를 사용하며, 이는 [16]을 따릅니다. 가중치는 [13]의 방식으로 초기화되며, 모든 평범한/잔차 네트워크는 처음부터 학습됩니다. 우리는 미니 배치 크기 256으로 SGD를 사용합니다. 학습률은 0.1에서 시작하여 오류가 정체되면 10배 감소하며, 모델은 최대 60만 회의 반복 동안 학습됩니다. 가중치 감쇠(weight decay)는 0.0001, 모멘텀(momentum)은 0.9로 설정됩니다. 우리는 [16]의 방식에 따라 드롭아웃(dropout)[14]을 사용하지 않습니다.

 

테스트에서는 비교 연구를 위해 표준 10-crop 테스트 방식을 사용합니다[21]. 최고의 결과를 위해, [41, 13]과 같이 완전 합성곱 형태를 채택하고, 여러 크기에서 점수를 평균화합니다(이미지는 짧은 변이 224, 256, 384, 480, 640이 되도록 크기 조정됩니다).

 

4. 실험

4.1. ImageNet 분류

우리는 ImageNet 2012 분류 데이터셋[36]에서 우리의 방법을 평가합니다. 이 데이터셋은 1000개의 클래스로 구성되어 있습니다. 모델은 128만 개의 학습 이미지로 훈련되며, 5만 개의 검증 이미지에서 평가됩니다. 최종 결과는 10만 개의 테스트 이미지에서 테스트 서버에 의해 보고됩니다. 우리는 top-1과 top-5 오류율을 모두 평가합니다.

 

평범한 네트워크(Plain Networks): 먼저 18층과 34층 평범한 네트워크를 평가합니다. 34층 평범한 네트워크는 Fig. 3(가운데)에 나와 있습니다. 18층 평범한 네트워크도 유사한 형태를 가지고 있습니다. 자세한 아키텍처는 표 1을 참조하십시오.

표 2의 결과는 더 깊은 34층 평범한 네트워크가 얕은 18층 평범한 네트워크보다 검증 오류가 더 높다는 것을 보여줍니다. 그 이유를 밝히기 위해, Fig. 4(왼쪽)에서는 훈련 절차 동안의 훈련 및 검증 오류를 비교했습니다. 우리는 성능 저하 문제를 관찰했는데, 34층 평범한 네트워크는 훈련 내내 더 높은 훈련 오류를 보였습니다. 이는 18층 네트워크의 해 공간이 34층 네트워크의 해 공간의 부분 집합임에도 불구하고 발생한 현상입니다.

 

이러한 최적화 어려움이 기울기 소실 문제에 기인하지 않았다고 주장합니다. 이 평범한 네트워크는 배치 정규화(BN)[16]를 사용하여 훈련되었으며, 이는 전방 전파된 신호가 0이 아닌 분산을 가지도록 보장합니다. 또한 역방향으로 전파되는 기울기들도 BN을 통해 적절한 크기를 유지함을 확인했습니다. 따라서 전방 신호나 역방향 신호가 소실되지는 않습니다. 실제로 34층 평범한 네트워크는 여전히 경쟁력 있는 정확도를 달성할 수 있었습니다(표 3 참조). 이는 솔버가 어느 정도 작동하고 있음을 시사합니다. 우리는 깊은 평범한 네트워크가 지수적으로 낮은 수렴 속도를 가질 수 있다고 추측하며, 이로 인해 훈련 오류가 감소하는 데 어려움이 생길 수 있습니다. 이러한 최적화 어려움의 원인은 향후 연구될 예정입니다.

 

표 1. ImageNet을 위한 아키텍처

ImageNet 아키텍처가 표로 제공됩니다. 빌딩 블록은 괄호 안에 표시되어 있으며(Fig. 5 참조), 쌓인 블록의 수가 명시됩니다. 다운샘플링은 conv3 1, conv4 1, conv5 1에서 스트라이드 2를 사용하여 수행됩니다.

 

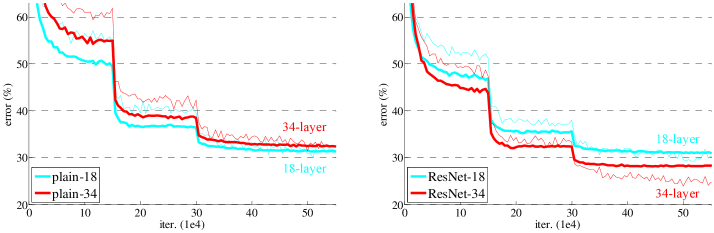
그림 4. ImageNet에서의 훈련

얇은 곡선은 훈련 오류를, 굵은 곡선은 중심 크롭(validation data의 일부)에 대한 검증 오류를 나타냅니다. 왼쪽은 18층과 34층 평범한 네트워크, 오른쪽은 18층과 34층 잔차 네트워크(ResNet)를 보여줍니다. 이 그래프에서 잔차 네트워크는 평범한 네트워크와 비교하여 추가적인 파라미터가 없습니다.

 

표 2. ImageNet 검증 데이터에서 top-1 오류(%, 10-crop 테스트)

여기서 ResNet은 평범한 네트워크와 비교하여 추가적인 파라미터가 없습니다. 훈련 절차는 Fig. 4에 나타나 있습니다.

잔차 네트워크(Residual Networks)

다음으로, 우리는 18층과 34층 잔차 네트워크(ResNets)를 평가합니다. 기본 아키텍처는 위에서 설명한 평범한 네트워크와 동일하지만, 각 3x3 필터 쌍에 단축 연결이 추가되었습니다(Fig. 3, 오른쪽 참조). 첫 번째 비교에서는(Table 2 및 Fig. 4 오른쪽), 모든 단축 연결에 대해 항등 매핑을 사용하고, 차원을 늘리기 위해 제로 패딩을 사용했습니다(옵션 A). 따라서 이들은 평범한 네트워크와 비교했을 때 추가적인 파라미터가 없습니다.

우리는 표 2와 Fig. 4에서 세 가지 주요 관찰을 할 수 있습니다.

1. 첫째, 잔차 학습에서는 상황이 역전됩니다. 34층 ResNet이 18층 ResNet보다 성능이 더 좋습니다(2.8% 차이). 더욱 중요한 점은, 34층 ResNet이 훈련 오류가 현저히 낮으며, 검증 데이터에 대해서도 일반화가 잘 이루어집니다. 이는 이 설정에서 성능 저하 문제가 잘 해결되었고, 깊이를 증가시킴으로써 정확도를 향상시킬 수 있었음을 나타냅니다.
2. 둘째, 평범한 네트워크와 비교했을 때, 34층 ResNet은 top-1 오류를 3.5% 줄였습니다(Table 2). 이는 훈련 오류의 성공적인 감소에서 기인합니다(Fig. 4 오른쪽 vs. 왼쪽). 이 비교는 매우 깊은 시스템에서 잔차 학습의 효과를 입증합니다.
3. 마지막으로, 18층 평범한/잔차 네트워크는 유사한 정확도를 보였지만(Table 2), 18층 ResNet은 더 빠르게 수렴했습니다(Fig. 4 오른쪽 vs. 왼쪽). 네트워크가 "너무 깊지 않으면"(여기서는 18층), 현재의 SGD 솔버는 평범한 네트워크에서도 좋은 해결책을 찾을 수 있습니다. 이 경우, ResNet은 초기 단계에서 더 빠른 수렴을 제공함으로써 최적화를 용이하게 합니다.

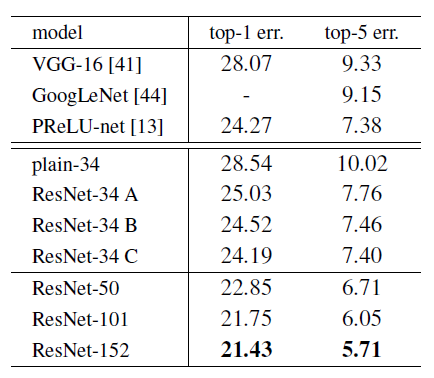
표 3: ImageNet 검증 데이터에서의 오류율 (%, 10-crop 테스트)

• VGG-16은 우리의 테스트를 기반으로 하였으며, ResNet-50/101/152는 차원을 늘릴 때만 사영(projections)을 사용하는 옵션 B를 사용했습니다.

표 4: ImageNet 검증 데이터셋에서의 단일 모델 결과에 대한 오류율 (%)

• 단, †로 표시된 항목은 테스트 셋에서 보고된 결과입니다.

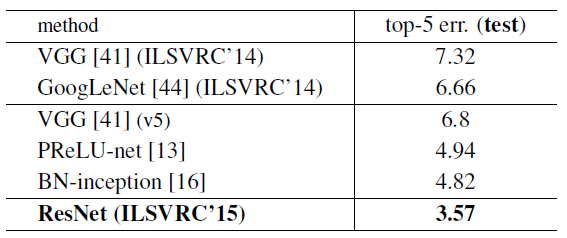
표 5: 앙상블에 대한 오류율 (%)

• top-5 오류율은 ImageNet 테스트 셋에서 나온 결과이며, 테스트 서버에 의해 보고되었습니다.

항등 vs. 사영 단축 연결

우리는 파라미터가 없는 항등 단축 연결이 훈련에 도움이 된다는 것을 보여주었습니다. 다음으로, 사영 단축 연결(Equation (2))을 조사합니다. 표 3에서는 세 가지 옵션을 비교합니다:

• (A) 차원을 늘릴 때 제로 패딩 단축 연결을 사용하고, 모든 단축 연결은 파라미터가 없습니다(표 2와 Fig. 4 오른쪽과 동일).
• (B) 차원을 늘릴 때 사영 단축 연결을 사용하고, 다른 단축 연결은 항등입니다.
• (C) 모든 단축 연결이 사영입니다.

표 3에 따르면, 세 옵션 모두 평범한 네트워크보다 훨씬 더 좋은 성능을 보였습니다. B는 A보다 약간 더 나은 성능을 보였습니다. 이는 A에서 제로 패딩된 차원들이 실제로는 잔차 학습을 하지 않기 때문이라고 주장합니다. C는 B보다 약간 더 나은 성능을 보였으며, 이는 열세 개의 사영 단축 연결이 도입한 추가적인 파라미터 때문이라고 생각됩니다. 그러나 A/B/C 간의 작은 성능 차이는 사영 단축 연결이 성능 저하 문제를 해결하는 데 필수적이지 않음을 시사합니다. 따라서 우리는 메모리/시간 복잡도와 모델 크기를 줄이기 위해 나머지 논문에서 옵션 C를 사용하지 않습니다. 항등 단축 연결은 아래에 소개된 병목 아키텍처의 복잡성을 증가시키지 않기 때문에 특히 중요합니다.

 

그림 5: 더 깊은 잔차 함수

왼쪽: ResNet-34를 위한 빌딩 블록(56x56 피처 맵)입니다. Fig. 3과 동일한 방식입니다.
오른쪽: ResNet-50/101/152를 위한 "병목" 빌딩 블록입니다.

 

더 깊은 병목 아키텍처 (Deeper Bottleneck Architectures)

이제 ImageNet을 위한 더 깊은 네트워크에 대해 설명합니다. 우리가 허용할 수 있는 훈련 시간에 대한 우려 때문에, 빌딩 블록을 병목(bottleneck) 설계로 수정합니다.
주석: 더 깊은 비병목 ResNet(예: Fig. 5 왼쪽)은 깊이를 증가시킴으로써 정확도를 향상시킬 수 있지만(CIFAR-10에서 보여준 바와 같이), 병목 ResNet만큼 경제적이지 않습니다. 따라서 병목 설계의 사용은 주로 실용적인 이유 때문입니다. 평범한 네트워크에서 나타나는 성능 저하 문제는 병목 설계에서도 관찰됩니다.

 

각 잔차 함수 F에 대해, 우리는 2층 대신 3층의 스택을 사용합니다(Fig. 5). 이 3층은 1x1, 3x3, 1x1 합성곱 층으로 구성되며, 1x1 층은 차원을 축소하고 다시 복원하는 역할을 하여 3x3 층이 입력 및 출력 차원이 작은 병목 역할을 하게 합니다. Fig. 5는 이 예시를 보여주며, 두 설계는 유사한 시간 복잡도를 가지고 있습니다.

 

파라미터가 없는 항등 단축 연결은 병목 아키텍처에서 특히 중요합니다. 만약 Fig. 5(오른쪽)의 항등 단축 연결이 사영 단축 연결로 대체된다면, 단축 연결이 고차원 입력과 출력에 연결되기 때문에 시간 복잡도와 모델 크기가 두 배가 될 수 있습니다. 따라서 항등 단축 연결은 병목 설계를 위한 더 효율적인 모델을 제공합니다.

• 50층 ResNet: 우리는 34층 네트워크의 각 2층 블록을 3층 병목 블록으로 교체하여 50층 ResNet을 만듭니다(표 1). 이 모델은 차원을 늘릴 때 옵션 B를 사용하며, 총 38억 FLOPs를 가집니다.
• 101층 및 152층 ResNet: 더 많은 3층 블록을 사용하여 101층 및 152층 ResNet을 구성합니다(표 1). 놀랍게도, 깊이가 크게 증가했음에도 불구하고 152층 ResNet(113억 FLOPs)은 여전히 VGG-16/19 네트워크(153억/196억 FLOPs)보다 복잡도가 낮습니다.

50층, 101층, 152층 ResNet은 34층 ResNet보다 상당히 더 높은 정확도를 보여줍니다(표 3 및 5). 우리는 성능 저하 문제를 관찰하지 않았으며, 깊이 증가로 인한 상당한 정확도 향상을 누리고 있습니다. 이러한 깊이의 이점은 모든 평가 지표에서 확인되었습니다(표 3 및 5).

 

그림 6: CIFAR-10에서의 훈련

• 점선은 훈련 오류를, 굵은 선은 테스트 오류를 나타냅니다.
• 왼쪽: 평범한 네트워크. Plain-110의 오류율은 60% 이상이며 표시되지 않았습니다.
• 가운데: ResNet.
• 오른쪽: 110층과 1202층의 ResNet.

최신 기법과의 비교

표 5에서 우리는 이전의 최고 단일 모델 결과들과 비교합니다. 우리의 기본 34층 ResNet은 매우 경쟁력 있는 정확도를 달성했습니다. 152층 ResNet은 단일 모델 기준으로 top-5 검증 오류율이 4.49%로, 이 단일 모델 결과는 이전의 모든 앙상블 결과를 능가합니다(표 5 참조). 우리는 서로 다른 깊이의 여섯 가지 모델을 결합하여 앙상블을 구성했으며(제출 당시 152층 모델 두 개 포함), 이를 통해 테스트 셋에서 top-5 오류율 3.57%를 기록했습니다(표 5). 이 결과는 ILSVRC 2015에서 1위를 차지했습니다.

4.2 CIFAR-10 및 분석

우리는 CIFAR-10 데이터셋[20]에 대해 더 많은 연구를 수행했습니다. 이 데이터셋은 10개의 클래스로 구성된 5만 개의 학습 이미지와 1만 개의 테스트 이미지로 이루어져 있습니다. 우리는 학습 셋에서 훈련하고 테스트 셋에서 평가된 실험을 제시합니다. 우리의 초점은 매우 깊은 네트워크의 동작을 분석하는 것이며, 최신 성과를 달성하는 데 있지 않기 때문에, 의도적으로 간단한 아키텍처를 사용했습니다.

 

평범한/잔차 아키텍처는 Fig. 3(가운데/오른쪽)의 형태를 따릅니다. 네트워크 입력은 32x32 이미지로, 픽셀별 평균을 차감한 후 입력됩니다. 첫 번째 층은 3x3 합성곱입니다. 이후, 피처 맵 크기 {32, 16, 8}에 대해 각각 3x3 합성곱을 가진 6n층의 스택을 사용하며, 각 피처 맵 크기마다 2n층을 사용합니다. 필터 수는 각각 {16, 32, 64}입니다. 서브샘플링은 스트라이드 2를 가진 합성곱에 의해 수행됩니다. 네트워크는 글로벌 평균 풀링층, 10-유형 완전 연결층, 그리고 소프트맥스 층으로 끝납니다. 총 6n+2개의 가중치 층이 쌓여 있습니다. 다음 표는 아키텍처를 요약합니다.

단축 연결이 사용될 때, 이들은 3x3 층의 쌍에 연결됩니다(총 3n개의 단축 연결). 이 데이터셋에서는 모든 경우에 항등 단축 연결(옵션 A)을 사용하므로, 우리의 잔차 모델은 평범한 네트워크와 정확히 동일한 깊이, 너비, 파라미터 수를 가집니다.

 

표 6: CIFAR-10 테스트 셋에서의 분류 오류

모든 방법은 데이터 증강을 사용했습니다. ResNet-110의 경우, 5번 실행한 결과를 제시하며, [43]과 동일하게 "최고 성능(평균 ± 표준 편차)"를 표시했습니다.

 

우리는 가중치 감쇠(weight decay) 0.0001과 모멘텀(momentum) 0.9를 사용하며, [13]의 가중치 초기화 방식과 BN(batch normalization)[16]을 적용하지만 드롭아웃(dropout)은 사용하지 않습니다. 이 모델들은 두 개의 GPU에서 미니 배치 크기 128로 훈련됩니다. 학습률은 0.1에서 시작하고, 32k 및 48k 반복에서 10배씩 감소시키며, 64k 반복에서 훈련을 종료합니다. 이 훈련 스케줄은 45k/5k의 훈련/검증 셋으로 나눈 결과에 따라 결정되었습니다. 우리는 훈련 시 [24]의 간단한 데이터 증강 방식을 따릅니다: 각 면에 4픽셀씩 패딩하고, 패딩된 이미지 또는 그 수평 뒤집기에서 32x32 크롭을 무작위로 샘플링합니다. 테스트 시에는 원본 32x32 이미지의 단일 뷰만 평가합니다.

 

우리는 n={3,5,7,9}을 비교하여 20, 32, 44, 56층 네트워크를 구성합니다. Fig. 6(왼쪽)은 평범한 네트워크의 동작을 보여줍니다. 깊이가 증가함에 따라 평범한 네트워크는 더 높은 훈련 오류를 보이며 최적화의 어려움을 겪습니다. 이 현상은 ImageNet(Fig. 4, 왼쪽)과 MNIST에서도 나타난 바 있으며[42], 이는 이러한 최적화 어려움이 근본적인 문제임을 시사합니다.

 

Fig. 6(가운데)는 잔차 네트워크(ResNets)의 동작을 보여줍니다. ImageNet 사례와 유사하게(Fig. 4, 오른쪽), 우리의 ResNet은 최적화 문제를 극복하고, 깊이가 증가할수록 정확도가 향상되는 것을 보여줍니다.

 

우리는 n=18을 탐구하여 110층 ResNet을 구성했습니다. 이 경우, 초기 학습률 0.1이 수렴을 시작하기에는 약간 크다는 것을 발견했습니다. 초기 학습률 0.1로는 몇 에포크 후에 수렴을 시작하지만(오류율 < 90%), 여전히 유사한 정확도에 도달합니다. 따라서 우리는 학습 초기에 학습률을 0.01로 설정하여 훈련 오류가 80% 이하로 떨어질 때까지(약 400회 반복) 워밍업을 한 후, 다시 0.1로 학습률을 올리고 훈련을 계속했습니다. 이후의 학습 스케줄은 이전과 동일하게 유지했습니다. 이 110층 네트워크는 잘 수렴하였으며(Fig. 6, 가운데), FitNet[35]이나 Highway[42]와 같은 다른 깊고 얇은 네트워크보다 더 적은 파라미터를 가지면서도(표 6), 최첨단 성과 중 하나(6.43%, 표 6)에 포함되었습니다.

 

그림 7: CIFAR-10에서 층 반응의 표준 편차

그림 7은 CIFAR-10에서 층 반응의 표준 편차를 나타냅니다. 반응은 각 3x3 층의 출력이며, 이는 배치 정규화(BN) 이후 비선형 함수(ReLU/덧셈) 이전의 값입니다.

• 위쪽 그림: 층들이 원래 순서대로 표시됩니다.
• 아래쪽 그림: 반응이 내림차순으로 정렬되어 있습니다.

층 반응 분석

그림 7은 층 반응의 표준 편차(std)를 보여줍니다. 이 반응은 각 3x3 층의 출력으로, BN 이후 다른 비선형 함수(ReLU/덧셈) 이전의 값입니다. ResNet의 경우, 이 분석은 잔차 함수의 반응 강도를 보여줍니다. 그림 7에서 ResNet은 평범한 네트워크보다 일반적으로 더 작은 반응을 보입니다. 이러한 결과는 잔차 함수가 일반적으로 비잔차 함수보다 0에 더 가까울 수 있다는 우리의 기본 가설(Sec. 3.1)을 뒷받침합니다. 또한, 그림 7에서 ResNet-20, 56, 110을 비교한 결과로 볼 때, 더 깊은 ResNet은 반응 크기가 더 작아지는 경향이 있습니다. 더 많은 층이 있을 때, ResNet의 각 개별 층은 신호를 덜 수정하는 경향이 있습니다.

1000층 이상의 모델 탐구

우리는 1000층 이상의 매우 깊은 모델을 탐구했습니다. n=200으로 설정하여 1202층 네트워크를 만들었으며, 이는 위에서 설명한 방식으로 훈련되었습니다. 우리의 방법은 최적화의 어려움을 보이지 않았으며, 이 1202층 네트워크는 훈련 오류가 0.1% 미만(Fig. 6, 오른쪽)을 달성할 수 있었습니다. 테스트 오류 또한 비교적 양호하게 유지되었습니다(7.93%, 표 6).

 

그러나 이러한 매우 깊은 모델에는 여전히 해결되지 않은 문제가 있습니다. 이 1202층 네트워크의 테스트 결과는 110층 네트워크보다 더 나빴으며, 두 네트워크 모두 훈련 오류는 유사했습니다. 우리는 이것이 과적합 때문이라고 주장합니다. 1202층 네트워크는 이 작은 데이터셋에 비해 불필요하게 큰 크기(19.4M 파라미터)를 가지고 있을 수 있습니다. 이 데이터셋에서 최상의 결과를 얻기 위해서는 maxout[10]이나 dropout[14]과 같은 강력한 정규화를 적용해야 합니다([10, 25, 24, 35]). 이 논문에서는 maxout/dropout을 사용하지 않고, 깊고 얇은 아키텍처를 설계하여 단순히 정규화를 적용했으며, 최적화의 어려움에 중점을 두었습니다. 하지만 강력한 정규화와 결합하면 결과가 개선될 수 있으며, 이는 향후 연구에서 다룰 것입니다.

 

4.3 PASCAL 및 MS COCO에서의 객체 탐지

• 표 7: PASCAL VOC 2007/2012 테스트 셋에서 기본 Faster R-CNN을 사용한 객체 탐지의 mAP(평균 정확도) (%). 더 나은 결과는 표 11과 12를 참조하십시오.

• 표 8: COCO 검증 셋에서 기본 Faster R-CNN을 사용한 객체 탐지의 mAP(%). 더 나은 결과는 표 9를 참조하십시오.

우리의 방법은 다른 인식 작업에서도 좋은 일반화 성능을 보였습니다. 표 7과 8은 PASCAL VOC 2007 및 2012 [5], 그리고 COCO [26] 데이터셋에서의 객체 탐지 기본 결과를 보여줍니다. 우리는 Faster R-CNN [32]을 탐지 방법으로 채택했습니다. 여기서 우리는 VGG-16 [41]을 ResNet-101로 대체했을 때의 성능 향상에 주목합니다. 두 모델을 사용한 탐지 구현 방식(부록 참조)은 동일하므로, 성능 향상은 더 나은 네트워크 덕분에 이루어진 것입니다. 특히, 어려운 COCO 데이터셋에서 COCO의 표준 지표(mAP@[.5, .95])에서 6.0%의 증가를 얻었는데, 이는 상대적으로 28%의 성능 향상에 해당합니다. 이 성과는 전적으로 학습된 표현 덕분입니다.

 

깊은 잔차 네트워크를 기반으로, 우리는 ILSVRC & COCO 2015 대회의 여러 트랙에서 1위를 차지했습니다: ImageNet 탐지, ImageNet 위치 확인, COCO 탐지, 그리고 COCO 세분화. 자세한 내용은 부록에 있습니다.

 

부록 A: 객체 탐지 기본 모델

이 섹션에서는 Faster R-CNN [32] 시스템을 기반으로 한 우리의 객체 탐지 방법을 소개합니다. 모델은 ImageNet 분류 모델로 초기화된 후 객체 탐지 데이터로 미세 조정됩니다. 우리는 ILSVRC & COCO 2015 탐지 대회에서 ResNet-50/101을 실험했습니다.

 

VGG-16 [32]과 달리, 우리의 ResNet에는 숨겨진 완전 연결(fc) 층이 없습니다. 이를 해결하기 위해 "Conv 특징 맵 위의 네트워크(Networks on Conv feature maps, NoC)"[33] 아이디어를 채택했습니다. 우리는 이미지에 대해 16픽셀 이하의 스트라이드를 가지는 층들(conv1, conv2_x, conv3_x, conv4_x, 총 91개의 conv 층들)을 사용해 전체 이미지에서 공유되는 합성곱 특징 맵을 계산합니다(ResNet-101의 예시, 표 1 참조). 이 층들은 VGG-16의 13개 합성곱 층과 유사하게 동작하며, ResNet과 VGG-16 모두 동일한 총 스트라이드(16픽셀)를 가지는 conv 특징 맵을 사용합니다. 이 층들은 영역 제안 네트워크(RPN)와 Fast R-CNN 탐지 네트워크[7]에서 공유됩니다. RoI 풀링[7]은 conv5_1 이전에 수행되며, 이후 conv5_x 이상의 모든 층이 각 영역에 대해 적용되어 VGG-16의 fc 층 역할을 합니다. 최종 분류 층은 분류 및 박스 회귀층[7]으로 대체됩니다.

 

BN(Batch Normalization) 층 사용에 있어, 사전 학습 후 우리는 ImageNet 학습 셋에서 각 층의 BN 통계(평균 및 분산)를 계산합니다. 그런 다음, 객체 탐지에 대해 미세 조정하는 동안 BN 층을 고정시킵니다. 이로 인해 BN 층은 일정한 오프셋과 스케일을 가지는 선형 활성화 함수로 작동하며, BN 통계는 미세 조정 과정에서 업데이트되지 않습니다. 우리는 Faster R-CNN 훈련 시 메모리 소비를 줄이기 위해 주로 BN 층을 고정시켰습니다.

PASCAL VOC

[7, 32]의 방식에 따라, PASCAL VOC 2007 테스트 셋을 위해 우리는 VOC 2007의 5k trainval 이미지와 VOC 2012의 16k trainval 이미지를 사용해 훈련했습니다("07+12"). PASCAL VOC 2012 테스트 셋을 위해서는 VOC 2007의 10k trainval+test 이미지와 VOC 2012의 16k trainval 이미지를 사용해 훈련했습니다("07++12"). Faster R-CNN을 훈련할 때 사용하는 하이퍼파라미터는 [32]와 동일합니다. 표 8에 결과가 나와 있습니다. ResNet-101은 VGG-16보다 mAP가 3% 이상 향상되었습니다. 이 향상은 ResNet이 학습한 개선된 특징 덕분입니다.

MS COCO

MS COCO 데이터셋[26]은 80개의 객체 카테고리를 포함합니다. 우리는 PASCAL VOC 지표(mAP @ IoU = 0.5)와 COCO의 표준 지표(mAP @ IoU = .5:.05:.95)를 평가합니다. 우리는 훈련에 80k개의 학습 이미지를, 평가에 40k개의 검증 이미지를 사용합니다. COCO에 대한 탐지 시스템은 PASCAL VOC에 대한 것과 유사합니다. 우리는 8개의 GPU를 사용한 구현으로 COCO 모델을 훈련했으며, RPN 단계는 8개의 이미지(즉, GPU당 1개)의 미니 배치를 가지며 Fast R-CNN 단계는 16개의 이미지로 미니 배치를 구성했습니다. RPN 단계와 Fast R-CNN 단계는 모두 24만 회 반복 동안 학습률 0.001로 훈련되며, 이후 8만 회 반복 동안 학습률 0.0001로 학습됩니다.

 

표 8은 MS COCO 검증 셋에서의 결과를 보여줍니다. ResNet-101은 VGG-16보다 mAP@[.5, .95]가 6% 증가하였으며, 이는 상대적으로 28% 향상된 것입니다. 놀랍게도, mAP@[.5, .95]의 절대 증가치(6.0%)는 mAP@.5의 증가치(6.9%)와 거의 동일합니다. 이는 더 깊은 네트워크가 인식과 위치 추정 모두에서 성능을 향상시킬 수 있음을 시사합니다.

 

부록 B: 객체 탐지 향상

완전성을 위해 대회에서 이루어진 향상 사항을 보고합니다. 이러한 향상은 깊은 특징(deep features)에 기반하고 있으며, 따라서 잔차 학습(residual learning)으로부터 혜택을 받을 수 있습니다.

 

• 표 9: MS COCO에서 Faster R-CNN과 ResNet-101을 사용한 객체 탐지 향상.

• 표 10: PASCAL VOC 2007 테스트 셋에서의 탐지 결과. 기본 모델은 Faster R-CNN 시스템입니다. "baseline+++" 시스템은 표 9에 있는 박스 세부 조정, 문맥, 다중 스케일 테스트를 포함합니다.

• 표 11: PASCAL VOC 2012 테스트 셋에서의 탐지 결과(http://host.robots.ox.ac.uk:8080/leaderboard/displaylb.php?challengeid=11&compid=4). 기본 모델은 Faster R-CNN 시스템입니다. "baseline+++" 시스템은 표 9에 있는 박스 세부 조정, 문맥, 다중 스케일 테스트를 포함합니다.

MS COCO

박스 세부 조정(Box refinement): 우리의 박스 세부 조정은 부분적으로 [6]의 반복적인 위치 조정(iterative localization)을 따릅니다. Faster R-CNN에서는 최종 출력이 제안된 박스와 다른 회귀된 박스입니다. 따라서 추론 단계에서는 회귀된 박스에서 새로운 특징을 추출하고, 새로운 분류 점수와 회귀된 박스를 얻습니다. 이 300개의 새로운 예측을 원래의 300개의 예측과 결합합니다. 예측된 박스의 집합에 대해 교차 영역 비율(IoU) 임계값 0.3으로 비최대 억제(NMS)를 적용한 후, 박스 투표(box voting)를 수행합니다[6]. 박스 세부 조정은 mAP를 약 2점 향상시킵니다(표 9).

 

글로벌 문맥(Global context): 우리는 Fast R-CNN 단계에서 글로벌 문맥을 결합합니다. 전체 이미지의 conv 특징 맵을 고려하여, 전역 공간 피라미드 풀링(global Spatial Pyramid Pooling) [12]을 사용해 특징을 추출합니다. 이 풀링된 특징은 RoI 이후 층들로 전달되어 글로벌 문맥 특징을 얻습니다. 이 글로벌 특징은 원래의 각 영역별 특징과 연결된 후, 분류와 박스 회귀층으로 이어집니다. 이 새로운 구조는 종단 간(end-to-end)으로 학습됩니다. 글로벌 문맥은 mAP@.5를 약 1점 향상시킵니다(표 9).

 

다중 스케일 테스트(Multi-scale testing): 위의 모든 결과는 [32]와 같이 단일 스케일 학습/테스트에 의해 얻어졌으며, 이때 이미지의 짧은 변은 s=600 픽셀입니다. 다중 스케일 학습/테스트는 [12, 7]에서 특징 피라미드를 선택하거나 [33]에서 maxout 층을 사용하는 방식으로 개발되었습니다. 현재 구현에서는 [33]을 따라 다중 스케일 테스트를 수행했으며, 제한된 시간으로 인해 다중 스케일 학습은 수행하지 않았습니다. 또한 다중 스케일 테스트는 Fast R-CNN 단계에서만 수행되었고, RPN 단계에서는 수행되지 않았습니다. 학습된 모델로 이미지 피라미드에서 conv 특징 맵을 계산하고, 이미지의 짧은 변이 s∈{200,400,600,800,1000}인 피라미드를 사용합니다. 두 개의 인접한 스케일을 선택한 후, 이 두 스케일의 특징 맵에서 RoI 풀링과 후속 층들을 수행하며[33], 이 특징들은 [33]과 같이 maxout으로 병합됩니다. 다중 스케일 테스트는 mAP를 2점 이상 향상시킵니다(표 9).

 

검증 데이터 사용: 이후 80k+40k trainval 세트를 사용하여 훈련하고 20k test-dev 세트로 평가합니다. 이 test-dev 세트는 공개적으로 사용할 수 있는 정답이 없으며, 결과는 평가 서버에 의해 보고됩니다. 이 설정 하에서 mAP@.5는 55.7%, mAP@[.5, .95]는 34.9%입니다(표 9). 이는 단일 모델의 결과입니다.

 

앙상블: Faster R-CNN에서 시스템은 영역 제안 학습과 객체 분류기를 동시에 학습하도록 설계되었으므로, 앙상블은 두 작업 모두에서 성능을 향상시킬 수 있습니다. 우리는 영역 제안을 위해 앙상블을 사용하고, 제안된 영역의 집합을 각 영역별 분류기 앙상블로 처리합니다. 표 9는 3개의 네트워크로 이루어진 앙상블을 기반으로 한 우리의 결과를 보여줍니다. test-dev 세트에서 mAP는 59.0%이고, mAP@[.5, .95]는 37.4%입니다. 이 결과는 COCO 2015 탐지 작업에서 1위를 차지한 결과입니다.

PASCAL VOC

우리는 위에서 설명한 모델을 기반으로 PASCAL VOC 데이터셋을 다시 분석했습니다. COCO 데이터셋에서 단일 모델로(표 9에서 55.7% mAP@.5), 우리는 이 모델을 PASCAL VOC 세트에서 미세 조정했습니다. 박스 세부 조정, 문맥, 다중 스케일 테스트의 향상점도 적용되었습니다. 이를 통해 PASCAL VOC 2007에서 85.6% mAP(표 11)와 PASCAL VOC 2012에서 83.8% mAP(표 11)를 달성했습니다. PASCAL VOC 2012의 결과는 이전 최신 결과[6]보다 10점 더 높습니다.

 

ImageNet 탐지

표 12: ImageNet 탐지 데이터셋에서 우리의 결과(mAP, %). 우리의 탐지 시스템은 Faster R-CNN [32]을 기반으로 하며, 표 9에서 설명한 향상된 방법을 적용하고 ResNet-101을 사용했습니다.

 

ImageNet Detection (DET) 작업은 200개의 객체 카테고리를 포함합니다. 정확도는 mAP@.5로 평가됩니다. ImageNet DET에 대한 우리의 객체 탐지 알고리즘은 표 9에 나와 있는 MS COCO에 대한 알고리즘과 동일합니다. 네트워크는 1000개 클래스로 이루어진 ImageNet 분류 데이터셋에서 사전 학습된 후, DET 데이터에서 미세 조정(fine-tuning)됩니다. 우리는 검증 셋을 [8]에 따라 val1/val2로 나누었고, DET 학습 셋과 val1 셋을 사용해 탐지 모델을 미세 조정했습니다. val2 셋은 검증에 사용되었습니다. 우리는 다른 ILSVRC 2015 데이터를 사용하지 않았습니다.

 

ResNet-101을 사용한 단일 모델은 DET 테스트 셋에서 58.8%의 mAP를 기록했으며, 3개의 모델로 구성된 앙상블은 62.1%의 mAP를 달성했습니다(표 12). 이 결과는 ILSVRC 2015에서 ImageNet 탐지 작업에서 1위를 차지했으며, 2위와 8.5포인트(절대값) 차이로 앞섰습니다.

 

부록 C: ImageNet 위치 추정(Localization)

표 13: ImageNet 검증에서의 위치 추정 오류(%). "GT 클래스에서의 LOC 오류" 열에서는 정답 클래스가 사용되었습니다([41]). "테스트" 열에서 "1-crop"은 224x224 픽셀의 중심 크롭에서 테스트하는 것을 의미하며, "dense"는 밀집(dense, 완전 합성곱) 및 다중 스케일 테스트를 의미합니다.

 

ImageNet 위치 추정(LOC) 작업 [36]은 객체의 분류와 위치 추정을 요구합니다. [40, 41]을 따라, 이미지 수준의 분류기가 먼저 이미지의 클래스 레이블을 예측한다고 가정하며, 위치 추정 알고리즘은 예측된 클래스에 기반하여 바운딩 박스만 예측합니다. 우리는 "클래스별 회귀" (per-class regression, PCR) 전략 [40, 41]을 채택하여 각 클래스에 대한 바운딩 박스 회귀자를 학습합니다. 네트워크는 ImageNet 분류를 위해 사전 학습된 후, 위치 추정을 위해 미세 조정됩니다. 우리는 제공된 1000개 클래스의 ImageNet 학습 데이터를 사용해 네트워크를 훈련합니다.

 

우리의 위치 추정 알고리즘은 몇 가지 수정 사항을 포함한 [32]의 RPN(RPN, Region Proposal Network) 프레임워크에 기반합니다. [32]에서 범주 비관적인 방식과 달리, 우리의 위치 추정을 위한 RPN은 클래스별로 설계되었습니다. 이 RPN은 [32]와 마찬가지로 이진 분류(cls)와 박스 회귀(reg)를 위한 두 개의 1x1 합성곱 층으로 끝납니다. 하지만 [32]와 달리, cls와 reg 층 모두 클래스별로 설계되었습니다. 구체적으로, cls 층은 1000차원의 출력을 가지며, 각 차원은 객체 클래스에 속하는지 여부를 예측하는 이진 로지스틱 회귀입니다. reg 층은 1000x4 차원의 출력으로 구성되며, 이는 1000개의 클래스에 대한 박스 회귀자를 포함합니다. [32]와 마찬가지로, 우리의 바운딩 박스 회귀는 각 위치에서 다중 평행 이동 불변 "앵커" 박스를 기준으로 이루어집니다.

 

ImageNet 분류 훈련(Sec. 3.4)에서와 같이, 데이터 증강을 위해 224x224 크기의 크롭을 무작위로 샘플링합니다. 미세 조정은 256개의 이미지로 이루어진 미니 배치 크기를 사용합니다. 음성 샘플이 지배적이 되는 것을 방지하기 위해, 각 이미지에서 8개의 앵커를 무작위로 샘플링하며, 이때 양성 및 음성 앵커는 1:1의 비율로 샘플링됩니다[32]. 테스트 시, 네트워크는 이미지 전체에 완전 합성곱 방식으로 적용됩니다.

 

표 14: 최신 기법과의 ImageNet 데이터셋에서의 위치 추정 오류(%) 비교

표 13은 위치 추정 결과를 비교한 내용입니다. [41]에 따라, 우리는 먼저 분류 예측으로 정답 클래스를 사용하는 "오라클" 테스트를 수행합니다. VGG 논문 [41]은 정답 클래스를 사용한 중심 크롭(center-crop) 오류가 33.1%라고 보고했습니다(표 13). 동일한 설정에서, ResNet-101을 사용하는 우리의 RPN 방법은 중심 크롭 오류를 13.3%로 크게 줄였습니다. 이 비교는 우리의 프레임워크가 뛰어난 성능을 보인다는 것을 입증합니다. 밀집(fully convolutional) 및 다중 스케일 테스트를 사용했을 때, ResNet-101은 정답 클래스를 사용하여 11.7%의 오류를 기록했습니다. ResNet-101을 사용하여 클래스를 예측했을 때(4.6% top-5 분류 오류, 표 5), top-5 위치 추정 오류는 14.4%입니다.

 

위의 결과는 Faster R-CNN [32]의 제안 네트워크(RPN)에만 기반한 것입니다. 탐지 네트워크(Fast R-CNN [7])를 사용하여 결과를 개선할 수도 있습니다. 그러나 이 데이터셋에서 하나의 이미지에 주로 단일 객체가 포함되며, 제안된 영역이 서로 크게 겹치고 매우 유사한 RoI-풀링 특징을 가지는 경우가 많습니다. 그 결과, Fast R-CNN [7]의 이미지 중심 학습은 작은 변동을 가진 샘플을 생성하며, 이는 확률적 학습에는 바람직하지 않을 수 있습니다. 이러한 동기에서, 우리는 현재 실험에서 Fast R-CNN 대신 RoI 중심의 R-CNN [8]을 사용했습니다.

 

우리의 R-CNN 구현은 다음과 같습니다. 위에서 훈련한 클래스별 RPN을 학습 이미지에 적용하여 정답 클래스에 대한 바운딩 박스를 예측합니다. 이 예측된 박스는 클래스 의존적인 제안 역할을 합니다. 각 학습 이미지에 대해, 점수가 가장 높은 200개의 제안을 추출하여 R-CNN 분류기를 훈련하는 학습 샘플로 사용합니다. 이미지는 제안에서 크롭되고, 224x224 픽셀로 변형된 후 R-CNN [8]과 마찬가지로 분류 네트워크로 전달됩니다. 이 네트워크의 출력은 cls와 reg를 위한 두 개의 fc 층으로 구성되며, 또한 클래스별로 동작합니다. 이 R-CNN 네트워크는 학습 셋에서 미니 배치 크기 256으로 RoI 중심 방식으로 미세 조정됩니다. 테스트 시, RPN은 각 예측 클래스에 대해 가장 높은 점수를 가진 200개의 제안을 생성하며, R-CNN 네트워크는 이 제안들의 점수와 박스 위치를 업데이트하는 데 사용됩니다.

 

이 방법은 top-5 위치 추정 오류를 10.6%로 줄였습니다(표 13). 이는 검증 셋에서 단일 모델 결과입니다. 분류와 위치 추정 모두에 대해 네트워크 앙상블을 사용하면, 테스트 셋에서 top-5 위치 추정 오류가 9.0%로 감소합니다. 이 수치는 ILSVRC 2014 결과(표 14)를 크게 능가하며, 64%의 상대적 오류 감소를 보여줍니다. 이 결과는 ILSVRC 2015에서 ImageNet 위치 추정 작업에서 1위를 차지했습니다.

-----------------------------------------------------------------------------------------------------------------------------------------------------------------

Maxout 층은 2013년 Ian Goodfellow와 그의 동료들이 제안한 신경망 활성화 함수의 일종입니다. Maxout 층은 ReLU나 sigmoid 같은 전통적인 활성화 함수와 달리, 각 뉴런에서 여러 선형 함수의 최대값을 선택하여 출력을 결정합니다.

 

 

Maxout 층의 특징

• 유연한 비선형성: Maxout 층은 비선형성을 잘 표현할 수 있어, 다양한 입력에 대해 더 유연하게 반응합니다. 이는 깊은 네트워크에서 매우 유용할 수 있습니다.
• 기울기 소실 문제 감소: ReLU와 비슷하게, Maxout 층은 기울기 소실 문제를 줄이는 데 도움이 됩니다. 이는 깊은 신경망에서 중요한 문제를 해결하는 데 기여할 수 있습니다.
• 더 많은 파라미터: Maxout 층은 더 많은 가중치와 편향을 필요로 하기 때문에, 더 큰 모델 크기와 더 많은 계산 자원을 필요로 할 수 있습니다.

Maxout은 특히 Dropout과 함께 사용될 때 성능이 좋다고 알려져 있으며, 이미지 분류와 같은 여러 응용 분야에서 성과를 보여주었습니다.

-----------------------------------------------------------------------------------------------------------------------------------------------------------------

 

 

1512.03385v1.pdf

0.78MB