https://arxiv.org/abs/1704.04861
MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications
We present a class of efficient models called MobileNets for mobile and embedded vision applications. MobileNets are based on a streamlined architecture that uses depth-wise separable convolutions to build light weight deep neural networks. We introduce tw
arxiv.org
초록
우리는 모바일 및 임베디드 비전 애플리케이션을 위한 효율적인 모델 클래스인 MobileNets를 소개한다. MobileNets는 가벼운 딥 뉴럴 네트워크를 구축하기 위해 깊이별 분리 합성곱(depthwise separable convolutions)을 사용하는 간소화된 아키텍처를 기반으로 한다. 우리는 지연(latency)과 정확도 사이에서 효율적으로 균형을 맞출 수 있는 두 가지 간단한 전역 하이퍼파라미터를 도입한다. 이러한 하이퍼파라미터는 문제의 제약 조건에 따라 모델 설계자가 애플리케이션에 맞는 크기의 모델을 선택할 수 있게 해준다. 우리는 자원과 정확도 간의 트레이드오프에 대한 광범위한 실험을 제시하며, ImageNet 분류에서 다른 인기 있는 모델들과 비교해 강력한 성능을 보여준다. 또한, 객체 탐지, 세밀한 분류, 얼굴 속성, 대규모 지리적 위치 확인 등 다양한 애플리케이션과 사용 사례에 걸쳐 MobileNets의 효과성을 입증한다.
1. 서론
알렉스넷(AlexNet)이 ImageNet 챌린지인 ILSVRC 2012에서 우승하면서 딥 컨볼루션 신경망을 대중화한 이후, 컨볼루션 신경망은 컴퓨터 비전 분야에서 보편화되었다. 일반적인 추세는 더 높은 정확도를 달성하기 위해 더 깊고 복잡한 네트워크를 만드는 것이다. 그러나 이러한 정확도 개선이 네트워크의 크기와 속도 측면에서 더 효율적인 것은 아니다. 로봇 공학, 자율 주행 자동차, 증강 현실과 같은 많은 실제 응용 프로그램에서는 제한된 계산 플랫폼에서 인식 작업이 적시에 수행되어야 한다.
이 논문은 모바일 및 임베디드 비전 애플리케이션의 설계 요구 사항에 쉽게 맞출 수 있는 매우 작고 지연 시간이 짧은 모델을 구축하기 위한 효율적인 네트워크 아키텍처와 두 가지 하이퍼파라미터 세트를 설명한다. 2장에서는 작은 모델을 구축하는 데 대한 이전 연구를 검토하고, 3장에서는 MobileNet 아키텍처와 더 작고 효율적인 MobileNet을 정의하는 폭 배율(width multiplier)과 해상도 배율(resolution multiplier)이라는 두 가지 하이퍼파라미터를 설명한다. 4장에서는 ImageNet과 다양한 애플리케이션 및 사용 사례에 대한 실험을 설명하며, 5장에서는 요약과 결론으로 마무리한다.

그림 1: MobileNet 모델은 효율적인 장치 내 인텔리전스를 위한 다양한 인식 작업에 적용될 수 있다.
2. 이전 연구
최근 문헌에서는 작은 크기와 효율적인 신경망을 구축하는 것에 대한 관심이 증가하고 있다. 다양한 접근 방식은 크게 두 가지로 나뉠 수 있는데, 하나는 사전 훈련된 네트워크를 압축하는 방법이고, 다른 하나는 처음부터 작은 네트워크를 직접 훈련시키는 방법이다. 본 논문은 모델 개발자가 애플리케이션의 자원 제약(지연 시간, 크기)에 맞는 작은 네트워크를 선택할 수 있게 하는 네트워크 아키텍처의 클래스를 제안한다. MobileNets는 주로 지연 시간 최적화에 중점을 두지만, 작은 네트워크도 제공한다. 많은 소형 네트워크 논문들은 크기만을 집중적으로 다루고 속도는 고려하지 않는다.
MobileNets는 주로 깊이별 분리 합성곱(depthwise separable convolutions)으로 구성되며, 이는 처음 [26]에서 소개되었고 이후 Inception 모델[13]에서 첫 몇 개의 층에서 계산량을 줄이기 위해 사용되었다. Flattened networks[16]는 완전하게 인수 분해된 합성곱으로 네트워크를 구축하여 극도로 인수 분해된 네트워크의 잠재력을 보여주었다. 이 논문과는 독립적으로, Factorized Networks[34]는 유사한 인수 분해된 합성곱과 함께 위상 연결(topological connections)의 사용을 소개했다. 이어서 Xception 네트워크[3]는 깊이별 분리 필터를 확장하여 Inception V3 네트워크보다 더 나은 성능을 보여주었다. 또 다른 소형 네트워크인 Squeezenet[12]는 병목 접근법을 사용하여 매우 작은 네트워크를 설계했다. 그 외에도 계산량을 줄인 네트워크에는 구조화된 변환 네트워크(structured transform networks)[28]와 deep fried convnets[37]가 있다.
작은 네트워크를 얻는 또 다른 접근 방식은 사전 훈련된 네트워크를 축소, 인수 분해 또는 압축하는 것이다. 제품 양자화(product quantization)[36], 해싱[2], 가지치기(pruning), 벡터 양자화 및 허프만 코딩[5]을 기반으로 한 압축 방식이 문헌에서 제안되었다. 또한, 사전 훈련된 네트워크를 가속화하기 위한 다양한 인수 분해 방법도 제안되었다[14, 20]. 소형 네트워크를 훈련시키는 또 다른 방법은 증류(distillation)[9]로, 더 큰 네트워크가 작은 네트워크를 가르치는 방식이다. 이는 우리의 접근 방식과 상호 보완적이며 4장에서 다룰 몇 가지 사용 사례에 포함되어 있다. 또 다른 새로운 접근 방식으로는 저비트 네트워크(low bit networks)[4, 22, 11]가 있다.
3. MobileNet 아키텍처
이 섹션에서는 먼저 MobileNet이 구축된 핵심 레이어인 깊이별 분리 필터(depthwise separable filters)를 설명한다. 그런 다음 MobileNet 네트워크 구조를 설명하고, 마지막으로 모델을 축소하는 두 가지 하이퍼파라미터인 폭 배율(width multiplier)과 해상도 배율(resolution multiplier)에 대한 설명으로 마무리한다.
3.1 깊이별 분리 합성곱 (Depthwise Separable Convolution)
MobileNet 모델은 깊이별 분리 합성곱(depthwise separable convolutions)을 기반으로 하며, 이는 표준 합성곱을 인수분해하여 깊이별 합성곱(depthwise convolution)과 1x1 합성곱(포인트와이즈 합성곱)으로 나누는 방식이다. MobileNets에서는 깊이별 합성곱이 각 입력 채널마다 하나의 필터를 적용하고, 포인트와이즈 합성곱은 1x1 합성곱을 사용하여 깊이별 합성곱의 출력을 결합한다. 표준 합성곱은 입력을 필터링하고 동시에 새로운 출력으로 결합하는 반면, 깊이별 분리 합성곱은 필터링과 결합을 두 개의 층으로 나눈다. 이러한 인수분해는 계산량과 모델 크기를 크게 줄이는 효과가 있다. 그림 2는 표준 합성곱(그림 2a)이 깊이별 합성곱(그림 2b)과 1x1 포인트와이즈 합성곱(그림 2c)으로 인수분해되는 방식을 보여준다.

표준 합성곱 연산은 합성곱 커널을 기반으로 특징을 필터링하고 이를 결합하여 새로운 표현을 생성하는 효과가 있다. 깊이별 분리 합성곱을 사용하면 이 필터링과 결합 단계를 두 단계로 나누어 계산 비용을 크게 줄일 수 있다.
깊이별 분리 합성곱은 두 개의 층으로 구성된다: 깊이별 합성곱과 포인트와이즈 합성곱이다. 깊이별 합성곱은 입력 채널마다 하나의 필터를 적용하고, 포인트와이즈 합성곱은 단순한 1x1 합성곱으로 깊이별 합성곱의 출력을 선형 결합한다. MobileNets는 이 두 층 모두에 배치 정규화(batchnorm)와 ReLU 비선형성을 사용한다.
깊이별 합성곱은 입력 채널마다 하나의 필터를 적용하며 다음과 같이 표현할 수 있다:

여기서 K는 깊이별 합성곱 커널이고, K의 m번째 필터는 의 m번째 채널에 적용되어 필터링된 출력 특징 맵 G의 m번째 채널을 생성한다.
깊이별 합성곱의 계산 비용은 다음과 같다:

깊이별 합성곱은 표준 합성곱에 비해 매우 효율적이지만 입력 채널을 필터링할 뿐, 새로운 특징을 생성하기 위해 결합하지 않는다. 따라서, 깊이별 합성곱의 출력에 대해 1x1 합성곱을 사용하여 새로운 특징을 생성하는 추가적인 층이 필요하다.
깊이별 합성곱과 1x1(포인트와이즈) 합성곱의 결합을 깊이별 분리 합성곱이라고 하며, 이는 처음 [26]에서 소개되었다.
깊이별 분리 합성곱의 비용은 다음과 같다:

이는 깊이별 합성곱과 1x1 포인트와이즈 합성곱의 비용을 더한 값이다.
합성곱을 필터링과 결합의 두 단계로 표현함으로써 계산 비용을 다음과 같이 줄일 수 있다:

MobileNet은 3x3 깊이별 분리 합성곱을 사용하며, 이는 표준 합성곱에 비해 약 8~9배 적은 계산량을 사용하면서도 정확도 저하는 미미하다. 4장에서 이러한 성능 차이를 확인할 수 있다.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------
깊이별 분리 합성곱(depthwise separable convolutions)의 핵심 목표는 계산 효율성을 극대화하기 위해 연산량과 파라미터 수를 줄이는 것입니다. 이를 위해 깊이별 분리 합성곱은 표준 합성곱에서 필터링과 결합 과정을 분리합니다.
구체적으로, 표준 합성곱에서는 각 입력 채널마다 여러 개의 필터가 적용되지만, 깊이별 분리 합성곱에서는 각 입력 채널마다 하나의 필터만 적용합니다(깊이별 합성곱). 그리고 이 필터링된 출력을 결합하기 위해 추가로 1x1 포인트와이즈 합성곱이 사용됩니다. 이러한 구조는 표준 합성곱에 비해 커널 수를 줄이고 계산량을 크게 줄이는 효과를 가지고 있습니다.
결과적으로, MobileNet 같은 모델에서 더 작은 크기의 네트워크를 만들 수 있고, 이를 통해 계산 비용과 메모리 사용을 줄이면서도 성능을 어느 정도 유지할 수 있습니다. 이 방식은 특히 모바일 및 임베디드 환경에서 매우 유용합니다.
import tensorflow as tf
from tensorflow.keras.layers import Conv2D, DepthwiseConv2D, Input, BatchNormalization, ReLU
# 입력 크기 정의 (224x224 이미지, 3채널)
input_shape = (224, 224, 3)
# 표준 합성곱
def standard_conv(input_shape):
inputs = Input(shape=input_shape)
# 32개의 3x3 커널을 사용한 표준 합성곱
x = Conv2D(32, (3, 3), padding='same')(inputs)
# 표준 합성곱 레이어는 전체 입력 채널(예: RGB 3채널)을 대상으로 32개의 필터를 적용하므로, 출력 텐서의 크기는 (224, 224, 32)처럼 될 것입니다.
x = BatchNormalization()(x)
x = ReLU()(x)
return tf.keras.Model(inputs, x)
# 깊이별 분리 합성곱
def depthwise_separable_conv(input_shape):
inputs = Input(shape=input_shape)
# 깊이별 합성곱 (각 채널별로 하나의 커널 적용)
x = DepthwiseConv2D((3, 3), padding='same')(inputs)
# 첫 번째 DepthwiseConv2D는 각 입력 채널에 대해 하나의 필터를 독립적으로 적용하므로, 출력 텐서의 크기는 입력 채널과 동일하게 유지됩니다. 예를 들어 입력이 (224, 224, 3)인 경우 출력도 (224, 224, 3)일 것입니다.
x = BatchNormalization()(x)
x = ReLU()(x)
# 1x1 포인트와이즈 합성곱 (채널 결합)
x = Conv2D(32, (1, 1), padding='same')(x)
# 두 번째 Conv2D(1x1) (포인트와이즈 합성곱)은 1x1 필터로 각 채널을 결합하여 출력 채널 수를 32개로 만듭니다. 따라서 출력 크기는 (224, 224, 32)로 변할 것입니다.
x = BatchNormalization()(x)
x = ReLU()(x)
return tf.keras.Model(inputs, x)
# 모델 생성
standard_model = standard_conv(input_shape)
depthwise_model = depthwise_separable_conv(input_shape)
# 모델 요약 출력
print("Standard Convolution Model Summary:")
standard_model.summary()
print("\nDepthwise Separable Convolution Model Summary:")
depthwise_model.summary()
- 깊이별 합성곱 (Depthwise Convolution): 이 단계는 각 입력 채널을 독립적으로 처리합니다.
- 입력: 224×224×3 (높이×너비×채널)
- 처리 과정:
- 빨간 채널에 3×3 필터 1개 적용
- 초록 채널에 3×3 필터 1개 적용
- 파란 채널에 3×3 필터 1개 적용
- 출력: 224×224×3 (각 채널이 독립적으로 처리되어 3개의 출력 채널 생성)
- 포인트와이즈 합성곱 (Pointwise Convolution): 이 단계는 깊이별 합성곱의 출력을 받아 채널 간 정보를 결합합니다.
- 입력: 224×224×3 (깊이별 합성곱의 출력)
- 처리 과정:
- 1×1×3 크기의 필터 32개 사용
- 각 공간 위치(224×224개의 위치)에서:
- 3개 채널의 값을 입력으로 받음
- 32개의 1×1×3 필터 각각과 연산
- 32개의 새로운 값 생성
- 출력: 224×224×32 (각 공간 위치에서 32개의 새 채널 값 생성)
즉, 다음과 같다.
- 표준 합성곱:
- 필터 개수: 32개 (예시의 경우)
- 각 필터 크기: 3x3x3 (높이 x 너비 x 입력 채널 수)
- 총 파라미터: 3 x 3 x 3 x 32 = 864
- 깊이별 분리 합성곱: a) 깊이별 합성곱 단계:
- 필터 개수: 3개 (입력 채널 수와 동일)
- 각 필터 크기: 3x3x1
- 파라미터: 3 x 3 x 3 = 27
- 필터 개수: 32개 (출력 채널 수와 동일)
- 각 필터 크기: 1x1x3
- 파라미터: 1 x 1 x 3 x 32 = 96
기억 안날 때, 보기 좋음. 이때 둘의 차이를 보이기는 건, 32개의 필터가 나타낼 수 있는 detail의 차이.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------
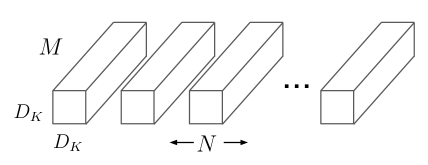
(a) 표준 합성곱 필터
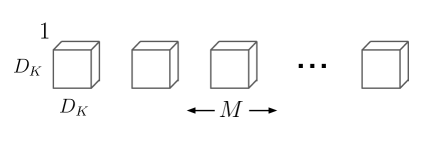
(b) 깊이별 합성곱 필터
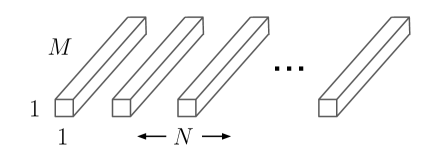
(c) 1x1 합성곱 필터(깊이별 분리 합성곱에서 포인트와이즈 합성곱이라 부름)
그림 2: (a)의 표준 합성곱 필터는 (b)의 깊이별 합성곱과 (c)의 포인트와이즈 합성곱으로 구성된 깊이별 분리 필터로 대체된다. 공간 차원에서 추가적인 인수 분해는 [16, 31]에서와 같이 많은 추가 계산을 절약하지 못하는데, 그 이유는 깊이별 합성곱에서 사용되는 계산량이 매우 적기 때문이다.
3.2 네트워크 구조와 훈련
MobileNet 구조는 앞서 설명한 깊이별 분리 합성곱을 기반으로 구축되었으며, 첫 번째 층만 완전한 합성곱을 사용한다. 네트워크를 이러한 간단한 방식으로 정의함으로써 네트워크 토폴로지를 쉽게 탐색할 수 있어 적절한 네트워크를 찾을 수 있다. MobileNet 아키텍처는 표 1에 정의되어 있다. 모든 층은 마지막 완전 연결 층을 제외하고 배치 정규화(batchnorm)와 ReLU 비선형성을 따른다. 마지막 층은 비선형성을 가지지 않으며 분류를 위해 소프트맥스 층으로 연결된다. 그림 3은 일반적인 합성곱, 배치 정규화 및 ReLU 비선형성을 사용하는 층과 깊이별 합성곱, 1x1 포인트와이즈 합성곱, 각 합성곱 층 이후의 배치 정규화 및 ReLU 비선형성을 포함하는 인수 분해된 층을 대조하고 있다. 다운샘플링은 깊이별 합성곱과 첫 번째 층에서의 스트라이드 합성곱으로 처리된다. 마지막 평균 풀링은 완전 연결 층 전에 공간 해상도를 1로 줄인다. 깊이별 및 포인트와이즈 합성곱을 각각의 층으로 계산하면, MobileNet은 28개의 층으로 구성된다.
단순히 연산량을 줄이는 것만으로는 충분하지 않다. 이러한 연산이 효율적으로 구현될 수 있는지도 중요한 요소다. 예를 들어, 비구조적 희소 행렬 연산은 희소성이 매우 높을 때까지는 일반적으로 밀집 행렬 연산보다 빠르지 않다. 우리의 모델 구조는 대부분의 계산을 밀집된 1x1 합성곱에 집중시킨다. 이는 고도로 최적화된 일반 행렬 곱(GEMM) 함수로 구현될 수 있다. 종종 합성곱 연산은 GEMM으로 구현되지만, 메모리에서 im2col이라 불리는 재정렬 작업을 거쳐 GEMM으로 매핑된다. 예를 들어, 이 방법은 인기 있는 Caffe 패키지에서 사용된다. 1x1 합성곱은 메모리 재정렬이 필요하지 않으며, 직접 GEMM으로 구현될 수 있는데, GEMM은 가장 최적화된 수치 선형 대수 알고리즘 중 하나이다. MobileNet의 경우, 전체 계산 시간의 95%가 1x1 합성곱에 사용되며, 매개변수의 75%도 1x1 합성곱에서 차지한다(표 2 참조). 추가적인 매개변수는 거의 모두 완전 연결 층에 있다.
MobileNet 모델은 TensorFlow [1]에서 RMSprop [33]을 사용해 비동기적 경사 하강법으로 훈련되었으며, 이는 Inception V3 [31]와 유사하다. 그러나 큰 모델 훈련과 달리, 작은 모델은 과적합 문제를 덜 겪기 때문에 규제와 데이터 증강 기법을 덜 사용했다. MobileNet을 훈련할 때는 사이드 헤드나 라벨 스무딩을 사용하지 않았고, Inception 훈련에서 사용되는 작은 크기의 자르기(crop) 크기를 제한함으로써 이미지 왜곡을 줄였다. 또한, 깊이별 필터에는 매개변수가 매우 적기 때문에 거의 가중치 감쇠(l2 규제)를 적용하지 않거나 매우 적게 적용하는 것이 중요했다. 다음 섹션에서의 ImageNet 벤치마크 실험에서는 모델의 크기와 상관없이 모든 모델을 동일한 훈련 파라미터로 훈련시켰다.
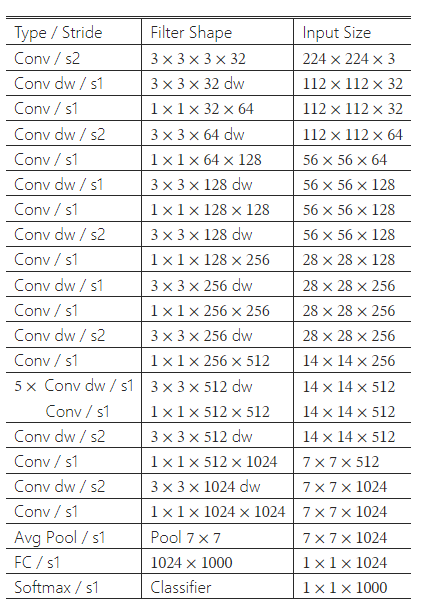
표 1: MobileNet 본체 아키텍처

그림 3: 왼쪽: 배치 정규화와 ReLU가 포함된 표준 합성곱층. 오른쪽: 깊이별 합성곱과 포인트와이즈 층이 있으며, 각 층 뒤에 배치 정규화와 ReLU가 이어지는 깊이별 분리 합성곱.
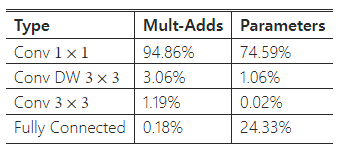
표 2: 각 층 유형별 자원 사용량
3.3 폭 배율(Width Multiplier): 더 얇은 모델
기본 MobileNet 아키텍처는 이미 작고 지연 시간이 적지만, 특정 사용 사례나 애플리케이션에서는 더 작고 빠른 모델이 필요할 때가 있다. 이러한 더 작은 모델을 만들기 위해 매우 간단한 매개변수인 폭 배율(α)을 도입한다. 폭 배율 α의 역할은 네트워크의 각 층을 균일하게 얇게 만드는 것이다. 주어진 층에서 폭 배율 α를 적용하면, 입력 채널 수 M은 αM으로, 출력 채널 수 N은 αN으로 변한다.
폭 배율 α가 적용된 깊이별 분리 합성곱의 계산 비용은 다음과 같다:

여기서 α는 (0, 1] 사이의 값이며, 일반적인 설정 값은 1, 0.75, 0.5, 0.25이다. α=1은 기본 MobileNet을 의미하고, α<1은 축소된 MobileNet을 의미한다. 폭 배율은 계산 비용과 매개변수 수를 대략 α^2만큼 줄이는 효과가 있다. 폭 배율은 어느 모델 구조에도 적용되어 합리적인 정확도, 지연 시간, 크기의 균형을 이루는 새로운 작은 모델을 정의할 수 있으며, 이 새로운 축소된 구조는 처음부터 다시 훈련되어야 한다.
3.4 해상도 배율(Resolution Multiplier): 축소된 표현
신경망의 계산 비용을 줄이는 두 번째 하이퍼파라미터는 해상도 배율 ρ이다. 이 배율은 입력 이미지에 적용되며, 그 결과 모든 층의 내부 표현도 동일한 배율로 축소된다. 실제로는 입력 해상도를 설정함으로써 ρ를 암묵적으로 설정하게 된다.
이제 우리는 폭 배율 α\alpha와 해상도 배율 ρ를 사용하여 네트워크의 핵심 층에 대한 계산 비용을 깊이별 분리 합성곱으로 표현할 수 있다:
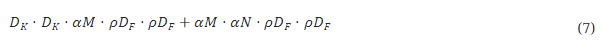
여기서 ρ∈(0,1]이며, 네트워크의 입력 해상도가 224, 192, 160 또는 128로 설정됨에 따라 암묵적으로 설정된다. ρ=1은 기본 MobileNet을 의미하고, ρ<1은 계산량이 축소된 MobileNet을 의미한다. 해상도 배율은 계산 비용을 ρ^2만큼 줄이는 효과가 있다.
예를 들어 MobileNet의 일반적인 층을 살펴보고, 깊이별 분리 합성곱, 폭 배율 및 해상도 배율이 어떻게 비용과 매개변수를 줄이는지 확인할 수 있다. 표 3은 표준 합성곱층에 아키텍처 축소 방법을 순차적으로 적용하면서 계산량과 매개변수 수를 보여준다. 첫 번째 행은 입력 특징 맵 크기가 14×14×512이고 커널 K의 크기가 3×3×512×5123인 완전한 합성곱층에 대한 Mult-Adds와 매개변수를 나타낸다. 다음 섹션에서는 자원과 정확도 간의 트레이드오프에 대해 자세히 살펴볼 것이다.
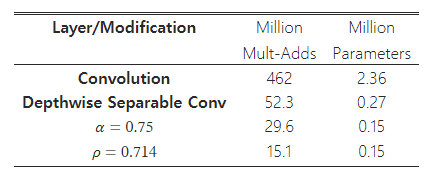
표 3: 표준 합성곱에 대한 수정 사항에 따른 자원 사용량. 각 행은 이전 행의 누적 효과를 반영한 결과이다. 이 예시는 MobileNet 내부 층에서D_K = 3, M = 512, N=512, D_F = 14일 때를 기준으로 한다.
- D_F: 특징 맵의 공간적 크기(너비와 높이)를 나타냅니다. 입력 또는 출력 특징 맵의 가로와 세로 길이를 의미하며, 예를 들어 D_F = 14이면 특징 맵의 크기가 14×14임을 뜻합니다.
- D_K: 합성곱 커널의 공간적 크기(너비와 높이)를 나타냅니다. 커널의 가로와 세로 길이를 의미하며, 예를 들어 D_K = 3이면 3×3 크기의 합성곱 필터를 사용하고 있음을 뜻합니다.
4. 실험
이 섹션에서는 먼저 깊이별 합성곱의 효과와, 네트워크의 레이어 수를 줄이는 대신 너비를 축소하는 방식의 선택에 대해 조사한다. 이후 두 가지 하이퍼파라미터인 폭 배율(width multiplier)과 해상도 배율(resolution multiplier)을 기반으로 네트워크를 축소하는 방법에 따른 트레이드오프를 보여주고, 여러 인기 있는 모델들과의 성능을 비교한다. 마지막으로 MobileNet을 다양한 응용 프로그램에 적용한 결과를 조사한다.
4.1 모델 선택
먼저 깊이별 분리 합성곱을 사용하는 MobileNet과 완전한 합성곱으로 구성된 모델을 비교한 결과를 제시한다. 표 4에서 볼 수 있듯이, 깊이별 분리 합성곱을 사용하는 경우, 완전한 합성곱을 사용하는 경우에 비해 ImageNet에서 정확도가 1%밖에 감소하지 않으면서도 계산량(Mult-Adds)과 매개변수 수를 크게 절감할 수 있었다.
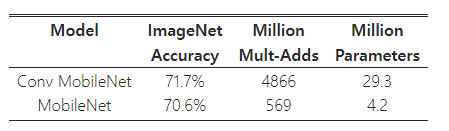
표 4: 깊이별 분리 합성곱 vs 완전 합성곱 MobileNet
다음으로, 폭 배율(width multiplier)을 사용하여 더 얇은 모델과 층 수를 줄여 더 얕은 모델을 비교한 결과를 제시한다. MobileNet을 더 얕게 만들기 위해, 표 1에서 특징 맵 크기가 14×14×512인 5개의 분리 필터 층을 제거했다. 표 5에서 볼 수 있듯이, 계산량과 매개변수 수가 유사한 상황에서 MobileNet을 얕게 만드는 것보다 얇게 만드는 것이 정확도에서 3% 더 나은 성능을 보였다.

표 5: 얇은 MobileNet vs 얕은 MobileNet
4.2 모델 축소 하이퍼파라미터
표 6은 폭 배율 α를 사용하여 MobileNet 아키텍처를 축소했을 때의 정확도, 계산량, 모델 크기 간의 트레이드오프를 보여준다. 정확도는 아키텍처가 너무 작아지는 α=0.25 지점까지는 부드럽게 감소한다.
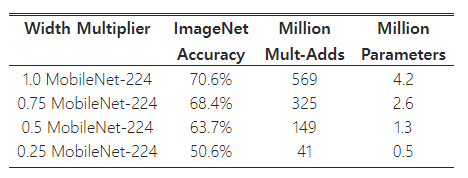
표 6: MobileNet 폭 배율
표 7은 입력 해상도를 줄여 훈련한 MobileNets에 대해 해상도 배율에 따른 정확도, 계산량, 모델 크기 간의 트레이드오프를 보여준다. 해상도가 줄어들면서 정확도도 점진적으로 감소한다.
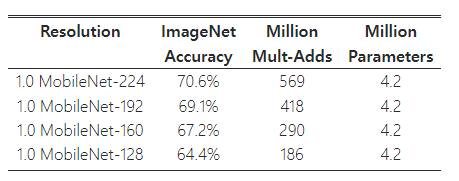
표 7: MobileNet 해상도 배율
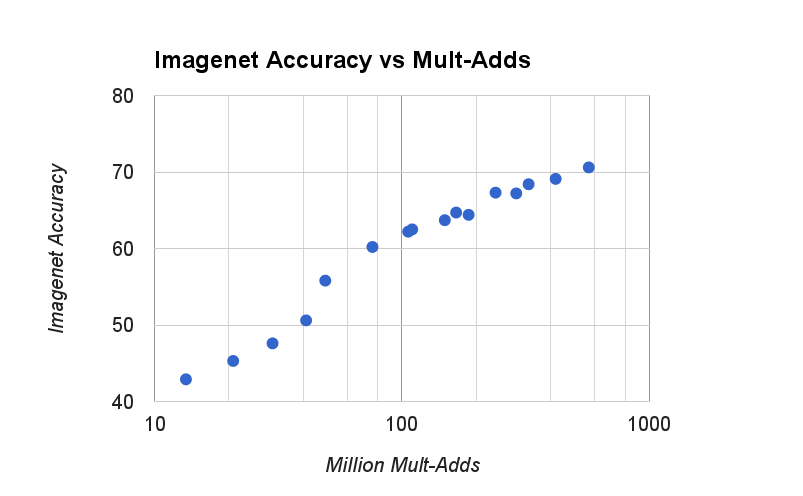
그림 4: 이 그림은 ImageNet 벤치마크에서 계산량(Mult-Adds)과 정확도 간의 트레이드오프를 보여준다. 정확도와 계산량 사이의 로그 선형 관계에 주목할 수 있다.
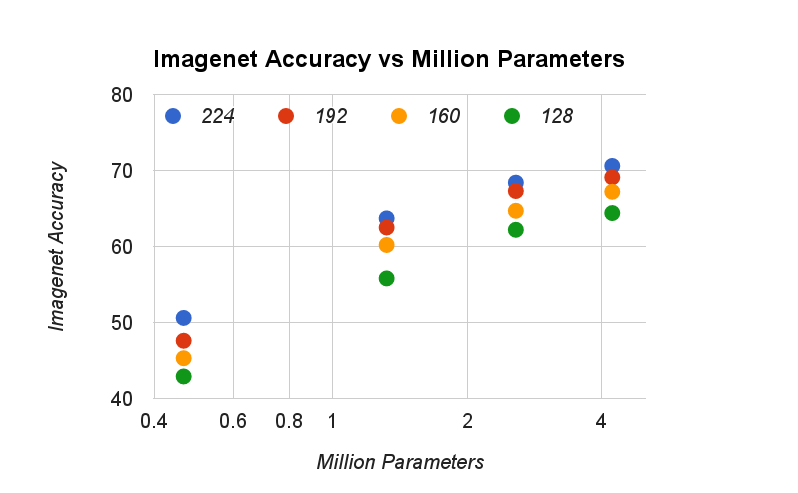
그림 5: 이 그림은 ImageNet 벤치마크에서 매개변수 수와 정확도 간의 트레이드오프를 보여준다. 색상은 입력 해상도를 나타낸다. 매개변수 수는 입력 해상도에 따라 변하지 않는다.
그림 4는 폭 배율 α∈{1,0.75,0.5,0.25}과 해상도 {224,192,160,128}의 조합으로 만든 16개의 모델에 대해 ImageNet 정확도와 계산량 간의 트레이드오프를 보여준다. 결과는 로그 선형 관계를 따르며, 모델이 매우 작아지는 α=0.25 지점에서 변화가 발생한다.
그림 5는 폭 배율 α∈{1,0.75,0.5,0.25}과 해상도 의 조합으로 만든 16개의 모델에 대해 ImageNet 정확도와 매개변수 수 간의 트레이드오프를 보여준다.
표 8은 완전한 MobileNet을 원래 GoogleNet [30] 및 VGG16 [27]과 비교한 결과를 보여준다. MobileNet은 VGG16과 거의 동일한 정확도를 제공하면서도 32배 더 작고 27배 적은 계산량을 요구한다. 또한 MobileNet은 GoogleNet보다 더 정확하면서도 크기는 더 작고 계산량은 2.5배 이상 적다.
표 9는 폭 배율 α=0.5와 해상도 160×160로 축소된 MobileNet을 비교한 결과를 보여준다. 축소된 MobileNet은 AlexNet [19]보다 4% 더 나은 성능을 보여주면서도 크기는 45배 작고 계산량은 9.4배 적다. 또한 Squeezenet [12]보다도 4% 더 나은 성능을 보여주며, 크기는 거의 동일하고 계산량은 22배 적다.
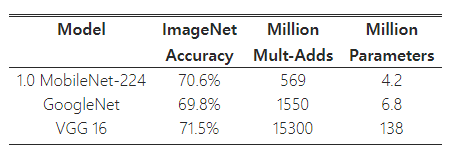
표 8: MobileNet과 인기 있는 모델의 비교
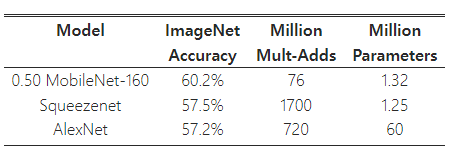
표 9: 더 작은 MobileNet과 인기 있는 모델들의 비교
4.3 세밀한 인식(Fine Grained Recognition)
우리는 MobileNet을 Stanford Dogs 데이터셋 [17]을 사용해 세밀한 인식 작업에 훈련시켰다. [18]의 접근 방식을 확장하여, [18]보다 더 크지만 노이즈가 있는 웹에서 수집한 훈련 데이터를 사용했다. 이 노이즈가 있는 웹 데이터를 사용해 세밀한 개 인식 모델을 사전 훈련한 뒤, Stanford Dogs 훈련 세트에서 모델을 미세 조정(fine-tuning)했다. Stanford Dogs 테스트 세트에서의 결과는 표 10에 나와 있다. MobileNet은 계산량과 모델 크기를 크게 줄이면서도 [18]의 최첨단 결과에 근접한 성능을 보여준다.
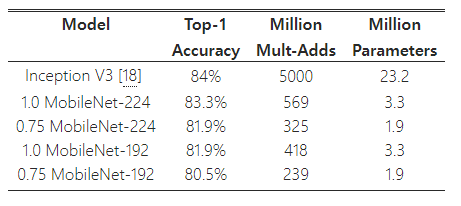
표 10: Stanford Dogs에서의 MobileNet 성능
4.4 대규모 지리적 위치 인식(Large Scale Geolocalization)
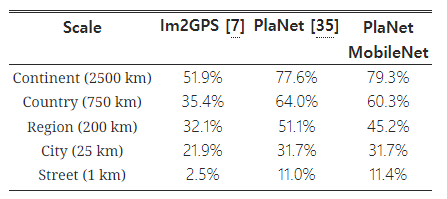
표 11: MobileNet 아키텍처를 사용한 PlaNet의 성능. 퍼센트는 Im2GPS 테스트 데이터셋에서 실제 위치와 특정 거리 이내로 정확하게 위치를 추정한 비율을 나타낸다. 원래 PlaNet 모델의 수치는 개선된 아키텍처와 훈련 데이터셋을 사용한 업데이트된 버전을 기반으로 하고 있다.
PlaNet [35]은 사진이 촬영된 위치를 알아내는 작업을 분류 문제로 다룬다. 이 접근 방식은 지구를 지리적 셀로 나누어 해당 셀을 대상 클래스(target class)로 설정하고, 수백만 장의 지오태그된(geo-tagged) 사진을 훈련시킨 컨볼루션 신경망을 사용한다. PlaNet은 다양한 사진을 성공적으로 위치 추정할 수 있으며, 같은 작업을 다루는 Im2GPS [6, 7]보다 뛰어난 성능을 보인다.
우리는 PlaNet을 동일한 데이터로 MobileNet 아키텍처를 사용해 다시 훈련시켰다. Inception V3 아키텍처 [31]를 기반으로 한 완전한 PlaNet 모델은 5200만 개의 매개변수와 57억 4000만 개의 Mult-Adds를 사용하지만, MobileNet 모델은 1300만 개의 매개변수와 0.58백만 개의 Mult-Adds만 사용한다. 여기서 MobileNet 모델의 300만 개 매개변수는 모델 본체에, 1000만 개는 최종 층에 해당한다. 표 11에서 볼 수 있듯이, MobileNet 버전은 훨씬 더 컴팩트하면서도 PlaNet에 비해 성능이 약간만 감소하며, 여전히 Im2GPS보다 훨씬 우수한 성능을 보여준다.
4.5 얼굴 속성
또 다른 MobileNet의 사용 사례는 훈련 절차가 불분명하거나 특이한 대형 시스템을 압축하는 것이다. 얼굴 속성 분류 작업에서, 우리는 MobileNet과 딥 네트워크를 위한 지식 전달 기법인 증류(distillation) [9]의 시너지 관계를 입증했다. 우리는 7500만 개의 매개변수와 16억 개의 Mult-Adds를 가진 대형 얼굴 속성 분류기를 축소하려고 한다. 이 분류기는 YFCC100M [32]과 유사한 다중 속성 데이터셋에서 훈련되었다.
우리는 MobileNet 아키텍처를 사용하여 얼굴 속성 분류기를 증류했다. 증류 [9]는 분류기가 실제 레이블 대신 더 큰 모델의 출력을 모방하도록 훈련시켜, 대형 또는 잠재적으로 무한한 비레이블 데이터셋으로부터 훈련할 수 있게 한다. 증류 훈련의 확장성과 MobileNet의 절제된 매개변수화를 결합한 최종 시스템은 정규화(예: 가중치 감쇠 및 조기 종료)를 필요로 하지 않으며, 성능 또한 향상된다. 표 12에서 볼 수 있듯이, MobileNet 기반의 분류기는 과감한 모델 축소에도 불구하고 각 속성에 대한 평균 정확도(mean AP)가 내부 개발한 모델과 유사하며, Mult-Adds는 1%만 소모한다.
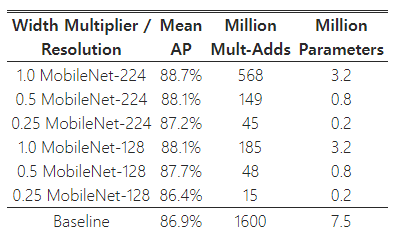
표 12: MobileNet 아키텍처를 사용한 얼굴 속성 분류. 각 행은 서로 다른 하이퍼파라미터 설정(폭 배율 α와 이미지 해상도)을 나타낸다.
4.6 객체 탐지(Object Detection)
MobileNet은 현대 객체 탐지 시스템에서 효과적인 기본 네트워크로 배치될 수 있다. 우리는 MobileNet이 COCO 데이터에서 객체 탐지를 위해 훈련된 결과를 보고하며, 이는 2016 COCO 챌린지에서 우승한 최근 연구 [10]를 기반으로 한다. 표 13에서는 MobileNet이 VGG 및 Inception V2 [13]와 함께 Faster-RCNN [23]과 SSD [21] 프레임워크에서 비교된다. 실험에서 SSD는 300 해상도(SSD 300)로 평가되었고, Faster-RCNN은 300 및 600 해상도(Faster-RCNN 300, Faster-RCNN 600)로 비교되었다. Faster-RCNN 모델은 이미지당 300개의 RPN 제안 상자를 평가한다. 모델들은 COCO의 train+val 데이터를 사용해 훈련되었으며, 8k의 미니밸(minival) 이미지를 제외하고 미니밸(minival) 데이터로 평가되었다. 두 프레임워크 모두에서 MobileNet은 계산 복잡성과 모델 크기의 일부만 사용하면서도 다른 네트워크와 비교할 만한 성능을 달성했다.

표 13: 다양한 프레임워크와 네트워크 아키텍처를 사용한 COCO 객체 탐지 결과 비교. mAP는 COCO의 주요 챌린지 메트릭(AP at IoU=0.50:0.05:0.95)으로 보고되었다.

그림 6: MobileNet SSD를 사용한 객체 탐지 결과 예시.
4.7 얼굴 임베딩(Face Embeddings)
FaceNet 모델은 최첨단 얼굴 인식 모델로, 삼중항 손실(triplet loss)을 기반으로 얼굴 임베딩을 구축한다 [25]. 모바일 환경에서 FaceNet 모델을 구축하기 위해, 우리는 FaceNet과 MobileNet의 훈련 데이터에서의 출력 간의 제곱 차이를 최소화하는 방식으로 증류(distillation)를 사용해 훈련을 진행한다. 매우 작은 MobileNet 모델의 결과는 표 14에 나와 있다.
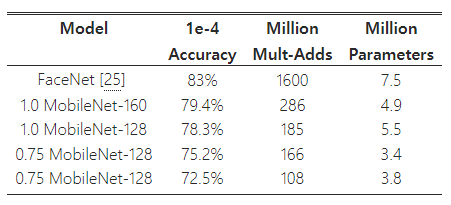
표 14: FaceNet에서 증류된 MobileNet
5. 결론
우리는 깊이별 분리 합성곱(depthwise separable convolutions)을 기반으로 한 새로운 모델 아키텍처인 MobileNets를 제안했다. 우리는 효율적인 모델을 설계하는 데 중요한 몇 가지 설계 결정을 조사했다. 그런 다음, 적절한 수준의 정확도를 희생하면서 크기와 지연 시간을 줄이기 위해 폭 배율(width multiplier)과 해상도 배율(resolution multiplier)을 사용하여 더 작고 빠른 MobileNets를 구축하는 방법을 보여주었다. 이후 다양한 MobileNets를 인기 있는 모델들과 비교하여, 크기, 속도, 정확도 측면에서 우수한 특성을 입증했다. 마지막으로 MobileNets가 다양한 작업에 적용될 때 효과적이라는 점을 시연했다. 다음 단계로는 MobileNets의 채택과 탐색을 돕기 위해 TensorFlow에서 모델을 공개할 계획이다.
'인공지능' 카테고리의 다른 글
| ImageNet Classification with Deep ConvolutionalNeural Networks (AlexNet) (2) | 2024.08.27 |
|---|---|
| SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <0.5MB model size (1) | 2024.08.22 |
| EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks (2) | 2024.08.20 |
| Deep Residual Learning for Image Recognition (1) | 2024.08.19 |
| Densely Connected Convolutional Networks (1) | 2024.08.18 |



