https://arxiv.org/abs/1606.08415
Gaussian Error Linear Units (GELUs)
We propose the Gaussian Error Linear Unit (GELU), a high-performing neural network activation function. The GELU activation function is $xΦ(x)$, where $Φ(x)$ the standard Gaussian cumulative distribution function. The GELU nonlinearity weights inputs by
arxiv.org

1. 서론
초기의 인공 뉴런들은 이진 임계 단위를 사용했습니다(Hopfield, 1982; McCulloch & Pitts, 1943). 이러한 강한 이진 결정은 시그모이드 활성화 함수로 부드럽게 처리되어, 뉴런이 "발화율"을 해석할 수 있게 하고 역전파로 훈련할 수 있도록 했습니다. 하지만 네트워크가 깊어짐에 따라 시그모이드 활성화 함수로 훈련하는 것이 비부드럽고 확률적이지 않은 ReLU(Nair & Hinton, 2010)보다 비효율적임이 밝혀졌습니다. ReLU는 입력의 부호를 기반으로 강한 게이팅 결정을 내리는데, 통계적 근거가 적음에도 불구하고 ReLU는 시그모이드보다 빠르고 더 나은 수렴을 자주 가능하게 하는 경쟁력 있는 엔지니어링 솔루션으로 남아있습니다. ReLU의 성공을 기반으로 최근 수정된 ELU(Clevert et al., 2016)는 ReLU와 같은 비선형성이면서도 음수 값을 출력할 수 있어 때때로 훈련 속도를 증가시키기도 합니다. 이처럼 활성화 함수의 선택은 신경망의 필수적인 아키텍처 결정으로 남아 있으며, 그렇지 않으면 네트워크는 단순한 심층 선형 분류기로 전락할 수 있습니다.
심층 비선형 분류기는 데이터를 매우 잘 맞출 수 있어 네트워크 설계자는 종종 은닉층에 노이즈를 추가하거나 드롭아웃(Srivastava et al., 2014)을 적용하는 등 확률적 정규화를 포함할지를 결정해야 합니다. 이 선택은 활성화 함수와는 별개입니다. 일부 확률적 정규화 기법은 네트워크를 네트워크 집합처럼 동작하게 만들어 가짜 집합(pseudoensemble)을 형성할 수 있으며, 이는 정확도를 크게 향상시킬 수 있습니다. 예를 들어, 확률적 정규화 기법인 드롭아웃은 몇몇 활성화 결정을 0으로 곱하여 임의로 변경함으로써 가짜 집합을 형성합니다. 따라서 비선형성과 드롭아웃은 뉴런의 출력을 함께 결정하지만, 이 두 혁신은 여전히 분리된 상태로 남아 있습니다. 더욱이, 대중적인 확률적 정규화 기법은 입력과 무관하게 작동하기 때문에 비선형성은 이러한 정규화 기법에 의해 보완됩니다.
이 연구에서는 새로운 비선형성인 Gaussian Error Linear Unit(GELU)을 소개합니다. 이는 확률적 정규화 기법과 관련이 있으며, Adaptive Dropout(Ba & Frey, 2013)을 수정한 형태의 기대값과 연관이 있습니다. 이는 뉴런의 출력을 보다 확률적인 관점에서 바라볼 수 있음을 시사합니다. 우리는 이 새로운 비선형성이 컴퓨터 비전, 자연어 처리, 음성 인식과 같은 다양한 작업에서 ReLU 또는 ELU를 사용하는 모델과 대등하거나 그 이상의 성능을 보임을 확인했습니다.


그림 1: GELU(μ=0, σ=1), ReLU, 그리고 ELU(α=1)
이 방식으로 입력을 마스킹하면 비결정론적인 특성을 유지하면서도 입력 값에 대한 의존성을 유지할 수 있습니다. 확률적으로 선택된 마스크는 입력에 대해 확률적인 0 또는 항등 변환(identity transformation)을 의미합니다. 이는 Adaptive Dropout(Ba & Frey, 2013)과 매우 유사하지만, Adaptive Dropout은 비선형성과 함께 사용되며 표준 정규 분포가 아닌 로지스틱 분포를 사용합니다. 우리는 어떠한 비선형성도 사용하지 않고 이 확률적 정규화 기법만으로도 경쟁력 있는 MNIST 및 TIMIT 네트워크를 훈련할 수 있음을 발견했습니다.


3. GELU 실험
우리는 GELU, ELU, 그리고 ReLU를 MNIST 분류(10개의 클래스를 가진 흑백 이미지, 6만 개의 훈련 샘플과 1만 개의 테스트 샘플), MNIST 오토인코딩, 트윗 품사 태깅(1000개의 훈련 샘플, 327개의 검증 샘플, 500개의 테스트 트윗), TIMIT 프레임 인식(3696개의 훈련 음성 문장, 1152개의 검증 음성 문장, 192개의 테스트 음성 문장), 그리고 CIFAR-10/100 분류(10/100개의 클래스를 가진 컬러 이미지, 5만 개의 훈련 샘플과 1만 개의 테스트 샘플)에서 평가했습니다. 우리는 LReLU와 같은 비선형성 함수는 ReLU와 유사하기 때문에 평가하지 않았습니다(LReLU에 대한 설명은 Maas et al. (2013)을 참조하십시오).
3.1 MNIST 분류

그림 2: MNIST 분류 결과.
왼쪽은 드롭아웃 없이, 오른쪽은 드롭아웃 비율 0.5에서의 손실 곡선을 보여줍니다. 각 곡선은 5번의 실행에서 중간값을 나타냅니다. 훈련 데이터의 로그 손실은 더 어두운 하단 곡선이며, 검증 데이터의 로그 손실 곡선은 더 희미하고 상단에 위치합니다.
이 비선형성이 이전 활성화 함수들과 경쟁할 수 있음을 검증하기 위해 Clevert et al. (2016)의 실험을 재현했습니다. 이를 위해, 우리는 GELU(μ=0, σ=1), ReLU, ELU(α=1)를 사용하여 완전 연결 신경망을 훈련시켰습니다. 각 8개 층으로 구성된, 128개의 뉴런을 가진 신경망은 배치 크기 128로 50에포크 동안 훈련되었습니다. 이 실험은 Clevert et al.의 실험과 다르게 Adam 옵티마이저(Kingma & Ba, 2015)를 사용하고, 모멘텀이 없는 확률적 경사 하강법 대신 사용했으며, 또한 비선형성이 드롭아웃에 얼마나 잘 대처하는지를 보여줍니다. 가중치는 단위 노름 행렬(unit norm rows)로 초기화되었으며, 이는 각 비선형성의 성능에 긍정적인 영향을 미친다는 연구(Hendrycks & Gimpel, 2016; Mishkin & Matas, 2016; Saxe et al., 2014)를 참고한 것입니다. 학습률은 { 10 − 3 , 10 − 4 , 10 − 5 } 범위에서 5천 개의 훈련 세트 검증 샘플을 사용해 튜닝되었으며, 5번의 실행에서 중간값을 사용했습니다. 이러한 분류기를 사용하여 그림 3에서 GELU를 사용하는 분류기가 잡음이 있는 입력에 더 강건할 수 있음을 보여줍니다. 그림 2는 GELU가 드롭아웃 유무에 관계없이 가장 낮은 중간값 훈련 로그 손실을 가지는 경향이 있음을 보여줍니다. 따라서, 비록 GELU가 다른 확률적 과정에서 영감을 받았지만 드롭아웃과 잘 조화됨을 알 수 있습니다.

그림 3: MNIST 강건성(robustness) 결과.
다양한 비선형성을 사용하여 입력에 잡음이 추가되었을 때 테스트 세트 정확도 감소와 로그 손실 증가를 기록했습니다. 드롭아웃 없이 훈련된 MNIST 분류기는 각 샘플에 서로 다른 수준의 잡음 Unif[−a,a]가 추가된 입력을 받았으며, 여기서 a=3이 가장 강한 잡음 세기입니다. 이 실험에서 GELU는 ELU 및 ReLU와 비교하여 동등하거나 그 이상의 강건성을 보여주었습니다.
3.2 MNIST 오토인코더
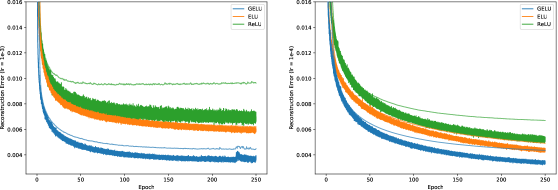
그림 4: MNIST 오토인코딩 결과.
각 곡선은 세 번의 실행에서 중간값을 나타냅니다. 왼쪽은 학습률 10^{-3}에서의 손실 곡선이며, 오른쪽 그림은 10^{-4}의 학습률에서의 결과를 보여줍니다. 얇고 연한 곡선은 테스트 세트의 로그 손실을 나타냅니다.
이제 자가 지도 학습(self-supervised learning) 설정에서 MNIST 데이터셋으로 심층 오토인코더를 훈련합니다(Desjardins et al., 2015). 이를 위해 네트워크는 1000, 500, 250, 30, 250, 500, 1000의 순서로 각 층의 너비를 설정한 구조를 사용합니다. 다시 Adam 옵티마이저와 배치 크기 64를 사용하며, 손실 함수는 평균 제곱 오차입니다. 학습률을 10^{-3}에서 10^{-4}로 조정하며, 학습률 0.01도 시도했지만 ELU는 발산하였고, GELU와 ReLU는 수렴이 잘 이루어지지 않았습니다. 그림 4의 결과는 GELU가 다양한 학습률을 수용하며 다른 비선형성 함수보다 성능이 우수하다는 것을 나타냅니다.
3.3 트위터 품사 태깅 (Twitter POS Tagging)
자연어 처리(NLP) 분야의 많은 데이터셋은 상대적으로 작기 때문에, 활성화 함수가 적은 예제로부터 잘 일반화하는 것이 중요합니다. 이러한 과제를 해결하기 위해 25개의 태그를 포함한 품사(POS)로 주석 처리된 트윗 데이터셋에서 비선형성을 비교합니다(Gimpel et al., 2011; Owoputi et al., 2013). 트윗 태거(tagger)는 5600만 개의 트윗 코퍼스에서 사전 학습된 단어 벡터를 사용하는 단순한 2층 신경망입니다(Owoputi et al., 2013). 입력은 태깅할 단어와 그 왼쪽 및 오른쪽 이웃 단어의 벡터를 연결한 것입니다. 각 층에는 256개의 뉴런이 있으며, 드롭아웃 유지 확률은 0.8이고, 네트워크는 Adam 옵티마이저로 최적화되며 학습률{10^{-3}, 10^{-4}에서 튜닝됩니다. 각 학습률에서 네트워크를 다섯 번씩 훈련한 결과, GELU의 테스트 세트 오류는 12.57%, ReLU는 12.67%, ELU는 12.91%로 나타났습니다.
3.4 TIMIT 프레임 분류 (Frame Classification)
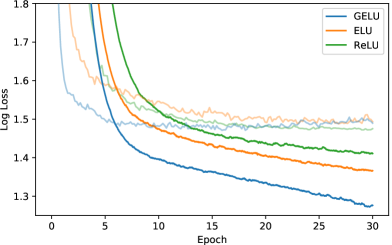
그림 5: TIMIT 프레임 분류.
학습 곡선은 훈련 세트의 수렴을 보여주며, 연한 곡선은 검증 세트의 수렴을 나타냅니다.
다음 과제는 TIMIT 데이터셋을 사용한 음소 인식입니다. TIMIT 데이터셋은 680명의 화자가 무잡음 환경에서 녹음한 데이터를 포함합니다. 이 시스템은 (Mohamed et al., 2012)에서와 같이 5개의 층으로 구성되고, 각 층은 2048개의 뉴런을 가진 분류기로, 39개의 출력 음소 레이블을 가지며 드롭아웃 비율은 (Srivastava, 2013)에서 제안된 0.5입니다. 이 네트워크는 입력으로 11개의 프레임을 받아서, 각 프레임당 26개의 MFCC, 에너지, 파생 특성을 사용하여 중심 프레임의 음소를 예측해야 합니다. 우리는 학습률 10^{-3}, 10^{-4}, 10^{-5}범위에서 튜닝을 수행하고, Adam 옵티마이저로 최적화했습니다. 각 설정에서 5번의 실험을 수행한 후 그림 5에서 중간값 곡선을 얻었으며, 가장 낮은 검증 오류에서 선택된 중간값 테스트 오류는 GELU가 29.3%, ReLU가 29.5%, ELU가 29.6%로 나타났습니다.
3.5 CIFAR-10/100 분류
다음으로, 더 복잡한 아키텍처에서도 GELU 비선형성이 다른 비선형성보다 다시 한 번 더 나은 성능을 발휘함을 보여줍니다. 우리는 얕고 깊은 합성곱 신경망에서 CIFAR-10과 CIFAR-100 데이터셋(Krizhevsky, 2009)을 사용하여 이 활성화 함수를 평가했습니다.
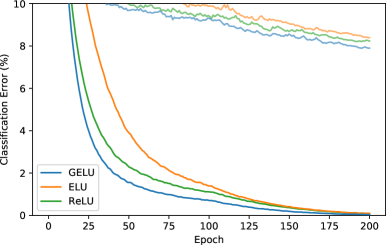
그림 6: CIFAR-10 결과.
각 곡선은 세 번의 실행에서 중간값을 나타냅니다. 학습 곡선은 훈련 세트의 오류율을 보여주며, 연한 곡선은 테스트 세트의 오류율을 나타냅니다.
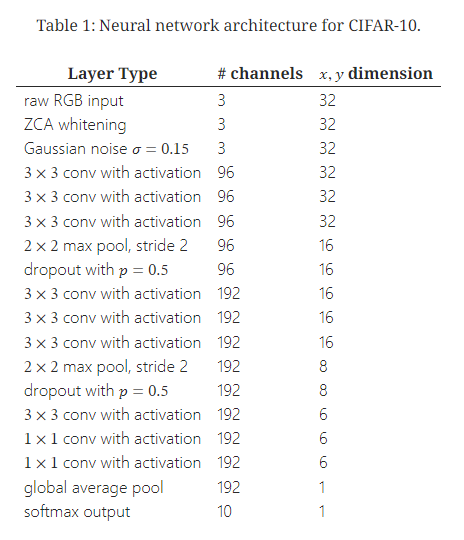
우리의 얕은 합성곱 신경망은 Salimans & Kingma(2016)의 아키텍처와 훈련 절차를 따르는 9개 층으로 이루어진 네트워크이며, 훈련 속도를 높이기 위해 배치 정규화를 사용합니다. 이 아키텍처는 부록 A에 설명되어 있으며, 최근에 데이터 증강 없이 CIFAR-10에서 최신 성능을 달성했습니다. 이 네트워크는 데이터 증강 없이 훈련되었습니다. 학습률 {10^{-3}, 10^{-4}, 10^{-5}을 튜닝하고, 5천 개의 검증 샘플을 사용한 후 교차 검증에서 선택된 학습률을 기반으로 전체 훈련 세트를 다시 훈련합니다. 네트워크는 200에포크 동안 Adam 옵티마이저로 최적화되며, 100번째 에포크에서 학습률이 선형적으로 0으로 감소합니다. 결과는 그림 6에 나타나 있으며, 각 곡선은 세 번의 실행 중 중간값입니다. 결국, GELU는 중간 오류율 7.89%를 기록했으며, ReLU는 8.16%, ELU는 8.41%를 기록했습니다.
다음으로, CIFAR-100에서 40개의 층과 4의 확장 계수를 가진 Wide Residual Network를 고려합니다(Zagoruyko & Komodakis, 2016). 우리는 Nesterov 모멘텀을 사용하고, 학습률 스케줄은 (Loshchilov & Hutter, 2016)에서 설명된 방식(T_0 = 50, η=0.1\)으로 50에포크 동안 훈련하며, 드롭아웃 유지 확률은 0.7입니다. 일부 연구에서는 ELU가 잔차 네트워크에서 기울기 폭발 문제를 일으킬 수 있다고 지적했으며(Shah et al., 2016), 이는 잔차 블록 끝에서 배치 정규화를 통해 완화할 수 있습니다. 따라서, 우리는 ELU를 공정하게 평가하기 위해 Conv-Activation-Conv-Activation-BatchNorm 블록 아키텍처를 사용했습니다. 세 번의 실행에서 중간값 수렴 곡선을 그림 7에서 얻었습니다. 그 결과, GELU는 중간 오류율 20.74%를 기록했으며, ReLU는 21.77%를 기록했습니다(원래 ReLU를 사용하는 40-4 WideResNet은 22.89%(Zagoruyko & Komodakis, 2016)를 기록했습니다). ELU는 22.98%를 기록했습니다.

그림 7: CIFAR-100 Wide Residual Network 결과.
학습 곡선은 드롭아웃을 적용한 훈련 세트의 수렴을 보여주며, 연한 곡선은 드롭아웃을 적용하지 않은 테스트 세트의 수렴을 나타냅니다.

그러나 GELU는 몇 가지 중요한 차이점도 가지고 있습니다. 이 비볼록(non-convex)하고 비단조(non-monotonic) 함수는 양의 영역에서 선형적이지 않으며, 모든 지점에서 곡률을 가지고 있습니다. 반면 ReLU와 ELU는 볼록하고 단조 증가하는 활성화 함수로, 양의 영역에서 선형적이어서 곡률을 가지지 않을 수 있습니다. 따라서 증가한 곡률과 비단조성은 GELU가 ReLU나 ELU보다 복잡한 함수들을 더 쉽게 근사할 수 있게 만들 수 있습니다. 또한 ReLU가 입력의 부호에 따라 입력을 게이트 처리하는 반면, GELU는 입력이 다른 값보다 얼마나 큰지에 따라 입력을 가중 처리합니다. 특히 중요한 점은, GELU는 확률적 정규화 기법의 기대값으로 해석될 수 있어 확률적 해석을 가질 수 있다는 점입니다.

5. 결론
이 논문에서 평가된 여러 데이터셋에서 GELU는 ELU와 ReLU의 정확도를 지속적으로 능가했으며, 이전의 비선형성 함수에 대한 유효한 대안이 될 수 있음을 확인했습니다.
감사의 말
NVIDIA Corporation에서 본 연구에 사용된 여러 TITAN X GPU를 기증해 주신 것에 대해 감사를 드립니다.
부록 A: CIFAR-10 실험을 위한 신경망 아키텍처
표 1: CIFAR-10을 위한 신경망 아키텍처.
부록 B: GELU와 SiLU의 역사




상황은 BERT와 GPT에서 GELU가 사용되기 시작하면서 변화하였고, 현재 GELU는 최첨단 트랜스포머의 기본 활성화 함수로 자리 잡았습니다. 이제 GELU는 SiLU보다 훨씬 더 자주 사용되고 있습니다.
따로 Reddit 게시물 "Google은 연구에서 공로 할당 문제를 가지고 있다"가 인기를 끌었으며, 그들은 SiLU를 swish라고 부르는 문제에 초점을 맞췄습니다. 예로 "Smooth Adversarial Training" 논문이 언급되었는데, 여기서 swish라는 용어가 SiLU 대신 사용되었습니다. swish 논문의 주요 저자는 이 게시물의 영향을 받아 논문을 업데이트하고 "swish"를 "SiLU"로 교체하며, 이 논문을 아이디어의 원천으로 인정했습니다. 이 게시물 이후로, TensorFlow와 PyTorch와 같은 인기 있는 라이브러리에서도 함수의 이름을 "swish"에서 "SiLU"로 변경하기 시작했습니다. 문제를 주의 깊게 살펴본 이들 사이에서는 이 문제가 대부분 해결되었으며, 우리는 이러한 공로가 대체로 인정된 것에 대해 감사하게 생각합니다.
'인공지능' 카테고리의 다른 글
| Diffusion Models Are Real-Time Game Engines (부록 추가 필요) (1) | 2024.09.09 |
|---|---|
| Deep Learning using Rectified Linear Units (ReLU) (2) | 2024.09.05 |
| GLU Variants Improve Transformer (SwiGLU) (3) | 2024.09.03 |
| Transfusion: Predict the Next Token and Diffuse Images with One Multi-Modal Model (2) | 2024.09.02 |
| 3D U-Net: Learning Dense Volumetric Segmentation from Sparse Annotation (1) | 2024.09.01 |



