https://arxiv.org/abs/1909.05840
Q-BERT: Hessian Based Ultra Low Precision Quantization of BERT
Transformer based architectures have become de-facto models used for a range of Natural Language Processing tasks. In particular, the BERT based models achieved significant accuracy gain for GLUE tasks, CoNLL-03 and SQuAD. However, BERT based models have a
arxiv.org
초록
Transformer 기반 아키텍처는 다양한 자연어 처리 작업에서 사실상의 표준 모델이 되었습니다. 특히, BERT 기반 모델은 GLUE 작업, CoNLL-03, SQuAD에서 상당한 정확도 향상을 달성했습니다. 하지만 BERT 기반 모델은 높은 메모리 사용량과 지연 시간이 발생하는 단점이 있어, 자원이 제한된 환경에서 이를 배포하는 데 어려움이 있습니다. 본 연구에서는 2차 헤시안 정보를 사용하여 미세 조정된 BERT 모델을 광범위하게 분석하고, 이를 바탕으로 BERT 모델을 초저정밀도로 양자화하는 새로운 방법을 제안합니다. 특히, 새로운 그룹별 양자화 방식을 제안하고, 헤시안 기반 혼합 정밀도 방법을 사용하여 모델을 추가로 압축합니다. 본 연구에서는 제안된 방법을 BERT의 하위 작업인 SST-2, MNLI, CoNLL-03, SQuAD에 대해 광범위하게 테스트했습니다. 결과적으로 2비트 초저정밀도 양자화로 모델 파라미터를 최대 13배, 임베딩 테이블 및 활성화를 최대 4배 압축하면서, 성능 저하가 최대 2.3% 이하로 기준 성능에 근접한 결과를 얻을 수 있었습니다. 모든 작업 중 SQuAD에 미세 조정된 BERT에서 가장 높은 성능 손실이 관찰되었습니다. 헤시안 기반 분석과 시각화를 통해, 이는 BERT의 현재 학습 및 미세 조정 전략이 SQuAD에서 수렴하지 않는다는 사실과 관련이 있음을 보여줍니다.
1. 서론
대규모 라벨 없는 데이터를 활용한 언어 모델 사전 학습은 BERT, XLNet, RoBERTa와 같은 모델의 핵심 동력이 되었습니다 [7, 38, 19]. Transformer [30]를 기반으로 하는 BERT 계열 [7] 모델은 다양한 자연어 처리(NLP) 작업에서 미세 조정 시 최신 성능을 크게 향상시킵니다 [23, 31]. 최근에는 이러한 연구 방향을 더욱 발전시키기 위해 수십억 개의 파라미터를 가진 모델로 확장하는 연구가 진행되고 있습니다 [22]. 이러한 모델들이 다양한 NLP 작업에서 최첨단 결과를 달성하고는 있지만, 높은 지연 시간과 막대한 메모리 사용량, 그리고 에지 추론을 위한 전력 소모 문제로 인해 셀폰이나 스마트 어시스턴트와 같은 임베디드 장치에서는 클라우드 연결이 필요하게 되는 제약이 따릅니다.
이 문제를 해결하기 위한 유망한 방법은 양자화(Quantization)입니다. 양자화는 파라미터 저장에 저비트 정밀도를 사용하여 저비트 하드웨어 연산을 통해 추론 속도를 높이는 방식입니다. 이를 통해 메모리 사용량이 줄어들고 추론 속도가 빨라져, FPGAs나 특정 도메인 가속기와 같은 저정밀도 추론을 지원하는 하드웨어에서 에지 배포가 가능해집니다. 하지만 초저비트 환경(예: 4비트)에서는 양자화된 모델의 일반화 성능이 크게 저하될 수 있으며, 이는 목표 응용에 적합하지 않을 수 있습니다. 기존의 컴퓨터 비전 분야에서는 이 문제를 해결하기 위한 연구가 활발하게 이루어져 왔으며, 다양한 양자화 방식 [15, 40], 혼합 정밀도 양자화 [8, 36, 43] 등이 이에 포함됩니다. 하지만 NLP, 특히 BERT 기반 모델에서는 이러한 모델 압축 및 가속이 더욱 필요함에도 불구하고 관련 연구가 매우 제한적입니다 [37, 33].
본 논문에서는 BERT 기반 모델의 초저정밀도 양자화에 중점을 두고, 하드웨어 효율성을 유지하면서 성능 저하를 최소화하는 것을 목표로 합니다. 이를 달성하기 위해 여러 새로운 기법을 도입하고, Q-BERT라는 방법을 제안합니다. 본 연구의 주요 기여는 다음과 같습니다:
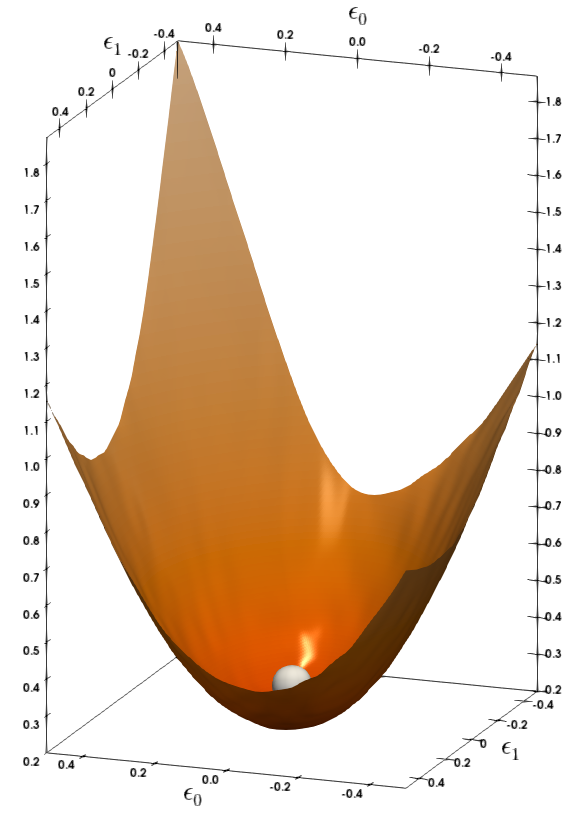
(a)MNLI 4th layer
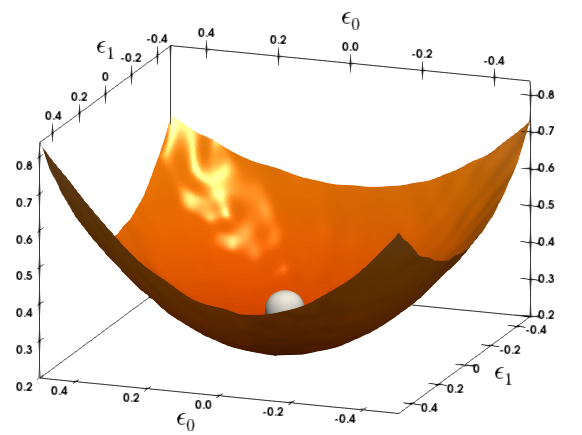
(b)MNLI 10th layer
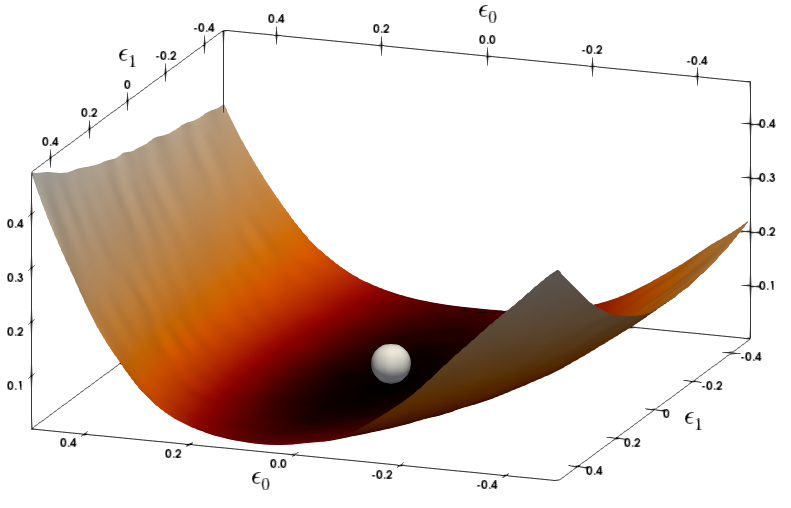
(c)CoNLL-03 4th layer
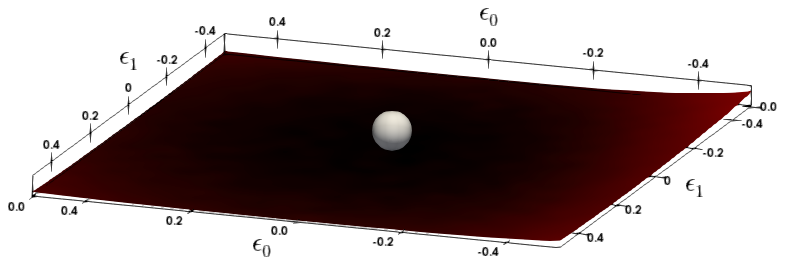
(d)CoNLL-03 11th layer
그림 1: MNLI와 CoNNL-03의 다양한 레이어에 대한 손실 지형을 Hessian의 첫 두 개 주요 고유벡터를 따라 파라미터를 변화시켜 시각화했습니다. 은색 구체는 BERT 모델이 수렴한 파라미터 공간의 지점을 나타냅니다. 더 평평한 곡률을 보이는 레이어는 더 낮은 비트 정밀도로 양자화할 수 있습니다.
- 우리는 BERT의 레이어별 2차 정보(Hessian 정보)를 통해 혼합 정밀도 양자화를 적용했습니다. BERT는 컴퓨터 비전 NN 모델과 비교할 때 [39, 8] 매우 다른 Hessian 거동을 보입니다. 따라서, [8]에서 평균 값만 사용한 것과 달리, 상위 고유값의 평균과 분산을 기반으로 민감도를 측정하여 더 나은 혼합 정밀도 양자화를 달성하고자 합니다.
- 우리는 하드웨어 복잡성을 크게 증가시키지 않으면서 정확도 저하를 완화할 수 있는 새로운 양자화 방식인 그룹별 양자화(group-wise quantization)를 제안합니다. 구체적으로, 그룹별 양자화 방식에서 우리는 각 행렬을 서로 다른 그룹으로 나누고, 각 그룹에 고유한 양자화 범위와 조회 테이블을 부여합니다.
- 우리는 BERT 양자화에서 발생하는 병목 지점을 조사하며, 특히 양자화 방식 및 임베딩, 셀프 어텐션, 완전 연결 계층 등 모듈이 NLP 성능과 모델 압축률 사이의 균형에 미치는 영향을 분석합니다.
Q-BERT를 감성 분류, 자연어 추론, 개체명 인식, 기계 독해 등 네 가지 하위 작업에서 평가하였습니다. Q-BERT는 가중치에서 13배, 활성화 크기에서 4배, 임베딩 크기에서 4배의 압축률을 달성하면서 정확도 손실을 최대 2.3% 이내로 유지했습니다. 우리가 아는 한, 허용 가능한 성능 손실로 초저비트 BERT 양자화를 구현한 연구는 본 논문이 처음입니다.

(a)SST-2

(b)MNLI
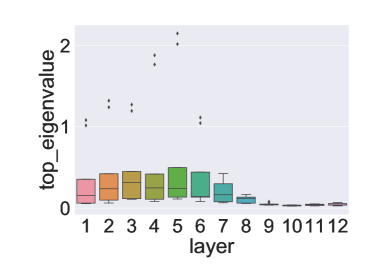
(c)CoNLL-03
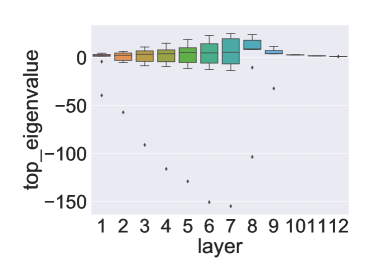
(d)SQuAD
그림 2: (a)에서 (d)까지는 SST-2, MNLI, CoNNL-03, SQuAD에 대해 각각 다양한 인코더 레이어에서의 상위 고유값 분포를 보여줍니다. 각 작업에서 데이터의 10%를 사용하여 상위 고유값을 계산하고, 10번의 개별 실행을 통해 상위 고유값 분포를 그렸습니다. 중간 레이어는 평균 값이 더 높고 다른 레이어보다 분산이 큰 경향을 보입니다. 마지막 세 개의 레이어는 모든 레이어 중에서 가장 낮은 분산과 평균 값을 가지고 있습니다.
2. 관련 연구
모델 압축
모델 압축은 매우 활발한 연구 분야로, 이 분야의 노력은 크게 다음과 같이 분류될 수 있습니다: (i) 컴팩트한 설계의 새로운 아키텍처 개발 [13, 11]; (ii) 지연 시간이나 모델 크기를 보상 함수로 설정한 자동 신경망 아키텍처 탐색(NAS) [32, 35]; (iii) 기존 아키텍처의 모델 크기를 줄이는 가지치기 기반 방법 [16, 18]; (iv) 대형 모델에서 작은 모델로 지식을 전달하여 더 컴팩트한 모델 학습을 돕는 지식 증류 [1, 10]; (v) 하드웨어와 아키텍처 공동 설계 [9]; (vi) 추론 양자화 [40, 8].
여기서는 양자화 [6, 24, 17, 42, 4, 14, 40, 8]에 중점을 둡니다. 초저정밀 양자화는 상당한 정확도 저하를 초래할 수 있다는 점이 주요 도전 과제입니다. 이 문제를 해결/완화하기 위해 혼합 정밀도 양자화 [36, 43, 32] 및 다단계 양자화 [41]가 제안되었습니다. 그러나 혼합 정밀도 양자화의 어려움은 검색 공간이 기하급수적으로 크다는 것입니다. 예를 들어 특정 레이어에 대해 세 가지 정밀도 옵션(2, 4, 8비트)이 있을 경우, 각각의 미세 조정된 BERT 모델 [7]의 총 검색 공간은 3^12≈5.3×10^5개의 서로 다른 정밀도 설정이 됩니다. 최근 [8]은 이러한 문제를 해결하기 위해 2차 민감도 기반 방법을 제안하여 컴퓨터 비전 작업에서 최신 성능을 달성했습니다. 본 논문의 일부는 이러한 이전 연구를 기반으로 하며, Hessian 스펙트럼의 평균 값만 사용하는 대신 2차 정보의 다양한 변형을 포함하여 결과를 확장합니다.
압축된 NLP 모델
NLP 모델 압축의 대표적인 예로는 기계 번역 및 언어 모델을 위한 LSTM 및 GRU 기반 모델이 있습니다 [37, 33]. 최근 Transformer 모델이 도입되면서 NLP 모델 크기가 크게 증가했습니다. 이는 Transformer에 매우 큰 완전 연결 계층과 어텐션 행렬이 포함되기 때문입니다 [30, 7, 38, 19, 22]. 이러한 모델을 자원이 제한된 환경에서 배포하기 위해 모델 압축이 필수적입니다. 이를 다룬 초기 연구로는 [21, 3]이 있습니다. 다른 접근법으로는 [29, 20]에서 Transformer의 셀프 어텐션 레이어를 가볍게 만들기 위해 아키텍처 변화를 탐구한 바 있습니다. 또한 [28, 27]에서는 BERT와 같은 대규모 사전 학습 Transformer 모델을 줄이기 위해 지식 증류(distillation)를 사용하는 시도도 있었습니다. 그러나 상대적으로 낮은 압축 비율인 4배에서도 상당한 정확도 손실이 발생했습니다. 본 연구에서는 임베딩 레이어의 4배 축소를 포함하여 압축 비율을 최대 13배까지 높이면서 성능 저하를 최소화할 수 있음을 보여줍니다.
3. 방법론
이 섹션에서는 제안하는 BERT 양자화 방법, 즉 Hessian 정보를 기반으로 한 혼합 정밀도 양자화와 그룹별 양자화 방식에 사용된 기법을 소개합니다.

BERTBASE 모델의 파라미터 크기는 임베딩이 91MB, 인코더가 325MB, 출력이 0.01MB입니다. 출력 레이어는 크기가 미미하여 양자화하지 않고, 임베딩과 인코더 레이어에 양자화를 적용합니다. Sec. 5.1에서 설명하겠지만, 임베딩 레이어가 인코더 레이어보다 양자화에 더 민감함을 발견했습니다. 따라서 임베딩과 인코더 파라미터를 각각 다른 방식으로 양자화합니다. 우리가 사용한 양자화 방식은 다음 섹션에서 자세히 설명합니다.
3.1 양자화 과정
일반적인 신경망 추론은 가중치와 활성화 모두 부동소수점 정밀도로 수행됩니다. 양자화는 네트워크 가중치를 다음과 같이 제한된 값 집합으로 변환합니다:

3.2 혼합 정밀도 양자화
각 인코더 레이어는 서로 다른 구조에 주의를 기울이며 [5], 따라서 각 레이어는 서로 다른 민감도를 보입니다. 모든 레이어에 동일한 비트 수를 할당하는 것은 최적이 아닙니다. 목표 모델 크기가 매우 작고, 4비트 또는 2비트와 같은 초저정밀도가 요구될 경우 이 문제는 더욱 중요해집니다. 따라서 성능을 유지하기 위해 민감한 레이어에 더 많은 비트를 할당하는 혼합 정밀도 양자화를 탐구합니다.

------------------
헤시안과 고유값의 의미
- 헤시안(Hessian): 모델의 손실 함수의 2차 미분 행렬로, 손실 함수의 곡률을 나타냅니다.
- 고유값: 헤시안의 고유값은 곡률의 크기를 의미합니다. 고유값이 크면 해당 레이어가 손실 함수의 변화에 민감하게 반응한다는 뜻이므로 양자화 시에 성능 손실이 발생할 가능성이 큽니다.
해당 layer의 미분 값을 바탕으로 양자화의 유무를 결정함.
------------------

(a)SQuAD 7th layer
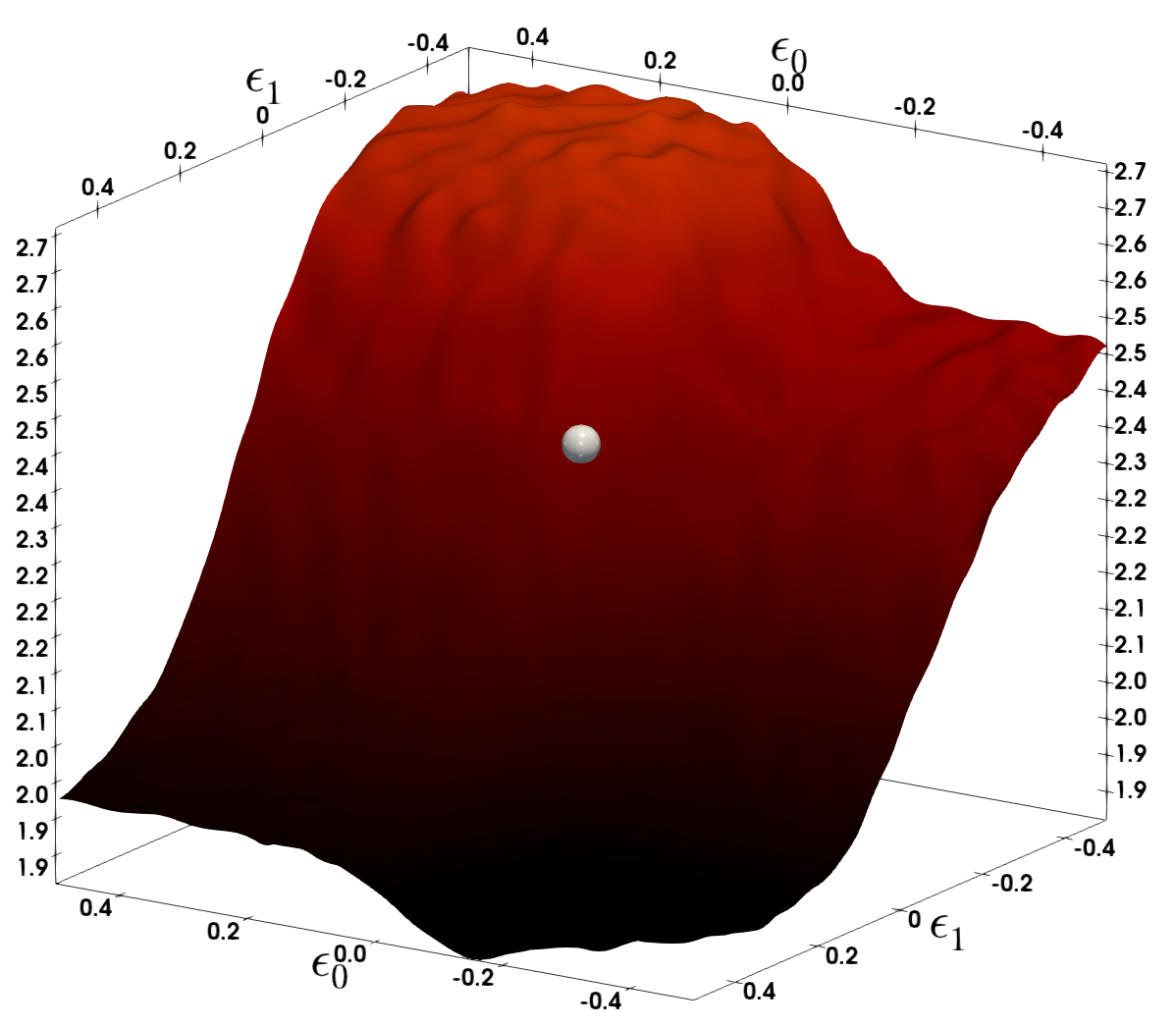
(b)SQuAD 11th layer
그림 3: SQuAD의 다양한 레이어에 대한 손실 지형을 Hessian의 상위 두 개 주요 고유벡터를 따라 파라미터를 변화시키면서 시각화했습니다. 은색 구체는 BERT 모델이 수렴한 파라미터 공간의 지점을 나타냅니다. SQuAD의 정지 지점에서는 두 레이어 모두 음의 고유값을 가지는 점에 주목하세요. 이는 양자화 후 SQuAD에서 상대적으로 더 큰 성능 저하가 관찰된 이유일 수 있습니다(표 1d 참조).
위의 헤시안 기반 접근법은 [8]에서 사용되었으며, 상위 고유값이 계산되고 다양한 훈련 데이터에 대해 평균화되었습니다. 상위 고유값이 작은 레이어에서는 더 평평한 손실 지형을 보이기 때문에(그림 1 참조) 더 공격적인 양자화가 수행되었습니다. 하지만, 상위 고유값의 평균만을 기준으로 비트를 할당하는 것은 많은 NLP 작업에 적합하지 않다는 것을 발견했습니다. 그림 2에 나타난 것처럼, 일부 레이어의 헤시안 상위 고유값은 입력 데이터셋의 다른 부분에 따라 매우 높은 분산을 보입니다. 예를 들어, SQuAD의 7번째 레이어의 분산은 61.6 이상으로 유지되지만, 해당 레이어의 평균은 약 1.0입니다. 이는 각 데이터 포인트가 전체 데이터셋의 10%(약 9천 샘플)에 해당함에도 불구하고 나타나는 현상입니다. 이를 해결하기 위해, 우리는 평균 값 대신 다음의 지표를 사용합니다:

우리 방법에서 강조해야 할 중요한 기술적 포인트는, 양자화를 수행하기 전에 학습된 모델이 국소 최솟값에 수렴해야 한다는 점입니다. 즉, BERT를 훈련하고 하위 작업에 대해 미세 조정한 실무자들이 국소 최솟값에 도달할 수 있도록 하이퍼파라미터와 반복 횟수를 적절히 선택했어야 합니다. 필요한 최적 조건은 기울기가 0이고, 곡률(즉, 헤시안 고유값)이 양수여야 한다는 것입니다. 우리의 분석에서는 MNLI, CoNLL-03, SST-2의 세 작업에 대해 상위 헤시안 고유값이 실제로 양수임을 확인했습니다(그림 1 및 부록의 그림 6 참조). 그러나, SQuAD에 대해 미세 조정된 BERT 모델은 국소 최솟값에 수렴하지 않았다는 것을 알 수 있었으며, 이는 그림 2(d)에 나타난 헤시안 고유값에서 큰 음수 고유값이 나타나는 것을 통해 확인할 수 있습니다. 손실 지형을 직접 시각화한 그림 3에서도 이를 명확히 볼 수 있습니다. 이러한 이유로, SQuAD에 양자화를 수행하면 다른 작업에 비해 더 큰 성능 저하가 발생할 것으로 예상하며, 이는 다음에서 논의될 바와 같이 실제로 그렇습니다.

(a)Layer-wise
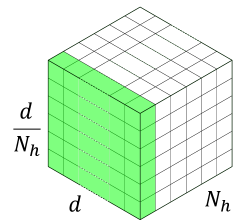
(b)Group-wise (N_h group)

(c)Group-wise (2N_h group)

3.3 그룹별 양자화


--------------------
- 전체 레이어를 하나의 그룹으로 양자화할 때:
- 모든 가중치를 동일한 범위로 압축해야 하므로, 큰 값이 많은 부분과 작은 값이 많은 부분을 동시에 표현하기가 어렵습니다. 이는 양자화 정밀도를 제한하고, 성능 저하로 이어질 수 있습니다.
- 각 행렬을 개별 그룹으로 양자화할 때 (특수한 그룹별 양자화):
- 각 행렬이 자체적으로 가중치 범위를 가질 수 있습니다. 예를 들어 Query, Key, Value, Output 행렬이 각각의 범위를 가지면, 양자화 정밀도가 더 높아져 성능을 유지하기 쉬워집니다.
- 출력 뉴런 단위로 나누는 경우 (일반적인 그룹별 양자화):
- 각 헤드 내에서 출력 뉴런을 서브 그룹으로 묶어 세밀하게 양자화합니다. 예를 들어, 각 헤드의 뉴런 64개를 6개씩 묶어 128개의 서브 그룹을 만들면, 각 서브 그룹이 고유한 양자화 범위를 가지므로 더 세밀하게 양자화할 수 있어 성능 저하를 최소화할 수 있습니다.
--------------------
4. 실험
이 섹션에서는 제안된 Q-BERT를 네 가지 NLP 작업에서 평가한 실험에 대해 설명합니다. 데이터셋에 대한 세부 정보는 부록 B에 있습니다. 우리가 아는 한, 현재 BERT 양자화에 대한 출판된 연구는 없으므로 혼합 정밀도 및 그룹별 양자화를 사용하지 않은 직접 양자화(Direct quantization, DirectQ)를 기준으로 보고합니다.
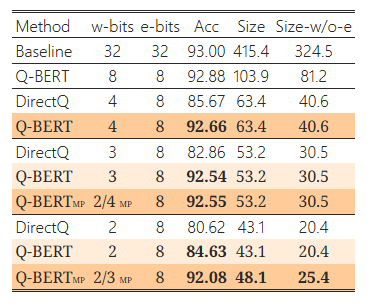
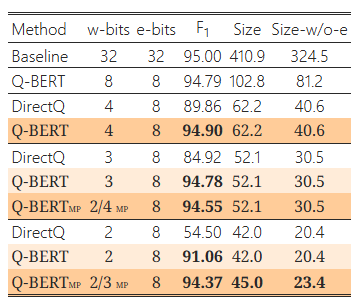
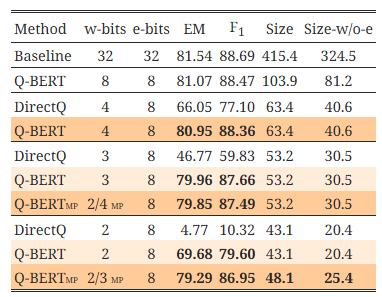
표 1: 자연어 이해 작업에서 BERTBASE의 양자화 결과
결과는 각 레이어에서 128개의 그룹을 사용하여 얻었습니다. 가중치에 사용된 양자화 비트를 "w-bits", 임베딩을 "e-bits", 모델 크기를 MB 단위로 "Size", 임베딩 레이어를 제외한 모델 크기를 "Size-w/o-e"로 축약합니다. 단순성과 효율성을 위해 기준 모델(Baseline)을 제외한 모든 모델은 8비트 활성화를 사용했습니다. 또한, Q-BERT를 혼합 정밀도 및 그룹별 양자화를 사용하지 않은 직접 양자화 방법(“DirectQ”)과 비교합니다. 여기서 "MP"는 혼합 정밀도 양자화를 나타냅니다.
(a)SST-2

(b)MNLI
(c)CoNLL-03
(d)SQuAD
4.1 주요 결과
Q-BERT의 결과를 SST-2, MNLI, CoNLL-03, SQuAD 네 가지 작업의 개발 세트에서 요약한 표 1d에 제시합니다. 보시는 바와 같이, Q-BERT는 모든 비트 설정에서 DirectQ 방법에 비해 모든 작업에서 유의미하게 더 나은 성능을 보입니다. 초저비트 설정에서 그 차이는 더욱 명확하게 나타납니다. 예를 들어, SQuAD의 4비트 설정에서 Direct 양자화(DirectQ)는 BERTBASE와 비교하여 성능이 11.5% 감소하지만, 동일한 4비트 설정에서 Q-BERT는 단지 0.5%의 성능 저하만을 보입니다. 또한 3비트 설정에서 Q-BERT와 DirectQ의 성능 차이는 다양한 작업에서 9.68%에서 27.83%까지 증가합니다.
더 낮은 비트 설정으로 정밀도를 추진하기 위해, 우리는 혼합 정밀도 Q-BERT (Q-BERTMP)를 조사했습니다. 보시다시피, Q-BERT가 균일한 2비트 설정일 때는 네 가지 작업 모두에서 성능이 매우 낮지만, 메모리는 3비트 설정 대비 20% 줄어듭니다. 이는 손실 지형 시각화에서 알 수 있듯이 모든 레이어가 동일한 양자화 민감도를 가지지 않기 때문입니다(그림 1 및 부록의 그림 6 참조). 직관적으로, 더 민감한 레이어에는 더 높은 비트 정밀도가 필요하고, 덜 민감한 레이어는 2비트 설정만으로도 충분합니다. BERTBASE의 각 인코더 레이어에 혼합 정밀도를 설정하기 위해, 우리는 그림 2에 나타난 헤시안의 상위 고유값의 평균과 분산을 모두 포함하는 식 (2)에 따라 민감도를 측정합니다. 그림 2의 모든 실험은 10회 실행을 기반으로 하며, 각 실행은 전체 훈련 데이터셋의 10%를 사용합니다. 대부분의 낮은 인코더 레이어(레이어 1-8)에서 마지막 세 레이어와 비교해 분산이 상당히 크다는 것을 알 수 있습니다. 일반적으로 중간 부분(레이어 4-8)이 가장 큰 mean(λ_i) 값을 가지며, 마지막 세 레이어는 상대적으로 더 작은 평균과 매우 작은 분산을 가지므로 민감도가 낮음을 나타냅니다. 따라서, Q-BERT 2/3 MP에서는 식 (2)에 따라 더 높은 비트를 중간 레이어에만 할당합니다.5 자세한 비트 설정은 부록 C.1에 포함되어 있습니다. 이 방식으로 메모리 저장소를 단지 5MB 추가함으로써 2/3비트 Q-BERTMP는 MNLI, SQuAD에서 2.3%, SST-2, CoNLL-03에서 1.1% 이내의 성능 저하를 유지하면서 가중치에서 최대 13배의 압축률을 달성할 수 있었습니다. 이는 균일한 2비트 Q-BERT보다 최대 7% 더 나은 성능입니다.
양자화 시 고려할 사항 중 하나는 3비트 양자화 실행이 일반적으로 하드웨어에서 지원되지 않는다는 점입니다. 그러나 3비트 양자화 값을 로드하고 실행 유닛에서 4 또는 8비트와 같은 더 높은 비트 정밀도로 변환하여 실행하는 것은 가능합니다. 이렇게 해도 DRAM으로부터의 메모리 양을 줄이는 장점이 있습니다. 또한, 3비트를 사용하지 않고 2비트와 4비트의 혼합을 사용하는 방법도 표 1d에서 보여준 바와 같이 가능합니다. 예를 들어, 혼합 2/4비트 정밀도 가중치를 가진 SST-2 Q-BERTMP는 3비트 양자화와 동일한 53.2MB 모델 크기를 가지며 비슷한 정확도를 달성합니다. 다른 작업에서도 유사한 경향을 관찰했습니다.
중요한 관찰 중 하나는 SQuAD가 다른 작업에 비해 양자화하기 어렵다는 점입니다(표 1d 참조). 예를 들어, 2비트 DirectQ의 경우 F1 점수가 10%에 불과합니다. Q-BERT조차도 다른 작업에 비해 더 큰 성능 저하를 겪고 있습니다. 우리는 헤시안 분석을 통해 이 현상을 추가로 연구했습니다. 그림 2에서 모든 작업 중 SQuAD가 고유값 분산이 더 클 뿐만 아니라 매우 큰 음수 고유값을 가진다는 점이 명확하게 나타납니다. 실제로 이는 SQuAD의 기존 BERT 모델이 국소 최솟값에 도달하지 않았음을 보여줍니다. 이는 그림 1 및 그림 3(부록의 그림 6 포함)의 네 가지 작업의 3차원 손실 지형에서도 더욱 명확히 나타납니다. 다른 세 작업에서는 정지 지점이 2차 곡면(헤시안의 첫 두 주요 고유값 방향에서 최소한)에서 나타나지만, SQuAD는 손실 지형이 완전히 다른 구조를 가지고 있습니다. 그림 3에서 보이는 바와 같이 SQuAD의 다양한 레이어의 정지 지점은 음의 곡률 방향을 가지고 있어 국소 최솟값에 아직 도달하지 않았음을 의미합니다. 이는 SQuAD의 양자화가 왜 더 많은 정확도 저하를 초래하는지를 잘 설명해줍니다. 학습 하이퍼파라미터를 변경하여 이를 해결하려는 초기 시도는 성공적이지 못했습니다. 우리는 BERT 모델이 훈련 데이터에 빠르게 과적합된다는 것을 발견했습니다. 그러나 BERT 모델 학습 자체를 수정하는 것은 이 논문의 범위를 벗어나며, 학술적 컴퓨팅 자원으로는 불가능합니다.
4.2 그룹별 양자화의 효과
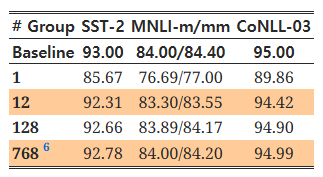
표 2에서 다양한 그룹 수에 따른 성능 향상을 측정했습니다. 표에서 볼 수 있듯이, 레이어별 양자화(Fig. 4a에 표시)는 모든 작업에서 최적이 아니며(4비트 가중치에서도 성능 저하가 약 7% 발생), 그룹 수를 늘릴수록 성능이 크게 향상됩니다. 예를 들어, 그룹 수를 12로 설정한 경우 모든 작업에서 성능 저하가 1% 미만입니다. 그룹 수를 12에서 128로 증가시키면 정확도가 최소 0.3% 증가합니다. 그러나 128에서 768로 그룹 수를 더 늘려도 성능 향상은 0.1% 이내에 그칩니다. 이는 그룹 수 128에서 성능 향상이 포화 상태에 도달함을 보여줍니다. 더 약한 양자화에서는 포화 그룹 수가 12와 같이 더 작을 수도 있습니다.
그룹 수가 너무 많으면 각 행렬 곱셈에 필요한 조회 테이블(LUT)의 수가 증가하여 하드웨어 성능에 부정적인 영향을 미칠 수 있고, 정확도 측면에서도 수익 체감이 발생합니다. 일관성을 위해 4.1절의 모든 실험에서 Q-BERT 및 Q-BERTMP에 128개의 그룹을 사용했습니다.
표 2: Q-BERT의 세 가지 작업에서의 그룹별 양자화 효과
모든 작업에서 가중치는 4비트, 임베딩과 활성화는 8비트로 설정했습니다. 위에서 아래로 갈수록 그룹 수가 증가하며, 정확도와 하드웨어 효율성을 균형 있게 유지하기 위해 다른 실험에서는 128개의 그룹을 설정했습니다.
5 논의
이 절에서는 단어 임베딩 및 위치 임베딩과 같은 다양한 임베딩 레이어를 포함한 여러 모듈에서 양자화의 영향을 추가로 조사하며, 주의 분포를 활용한 질적 분석을 수행합니다. 이를 통해 Q-BERT가 모든 경우에 DirectQ보다 원래 모델의 동작을 더 잘 반영함을 보여줍니다.
5.1 다양한 모듈에서의 양자화 효과
여기서는 BERT 모델의 다양한 모듈(다중 헤드 셀프 어텐션 vs. 피드포워드 네트워크, 단어 임베딩 vs. 위치 임베딩)에 대한 양자화 효과를 조사합니다.
일반적으로, 우리는 임베딩 레이어가 가중치보다 양자화에 더 민감하다는 것을 발견했습니다. 이는 표 3a에 나타나 있는데, 임베딩에 4비트 레이어별 양자화를 사용했을 때, SST-2, MNLI, CoNLL-03에서 최대 10%, SQuAD에서는 20% 이상의 성능 저하가 발생했습니다. 이는 가중치와 활성화를 8/8비트로 사용했음에도 불구하고 나타난 결과입니다. 반면에, 인코더 레이어는 전체 파라미터의 약 79%(임베딩 파라미터 크기의 4배)를 차지하지만, 표 1d에서 이들을 4비트로 양자화해도 성능 저하는 적었습니다.
또한, 위치 임베딩이 양자화에 매우 민감하다는 것을 발견했습니다. 예를 들어, 위치 임베딩을 4비트로 양자화할 경우 단어 임베딩을 양자화하는 것보다 성능 저하가 평균적으로 2% 더 큽니다. 이는 위치 임베딩이 전체 임베딩의 5% 미만을 차지함에도 불구하고 자연어 이해 작업에서 위치 정보가 중요한 역할을 한다는 것을 나타냅니다. 위치 임베딩이 모델 크기의 작은 부분만 차지한다는 점을 고려하여, 임베딩에 혼합 정밀도 양자화를 적용하여 허용 가능한 정확도 저하 범위 내에서 모델 크기를 추가로 줄일 수 있습니다(부록 C.2 참조).
표 3: 다양한 모듈에 대한 양자화 효과
단어 임베딩에 사용된 양자화 비트는 "ew-bits", 위치 임베딩은 "ep-bits", 다중 헤드 어텐션 레이어는 "s-bits", 완전 연결 레이어는 "f-bits"로 약어로 표기했습니다. (a)에서는 가중치와 활성화 비트를 8로 설정했습니다. (b)에서는 임베딩과 활성화 비트를 8로 설정했습니다.
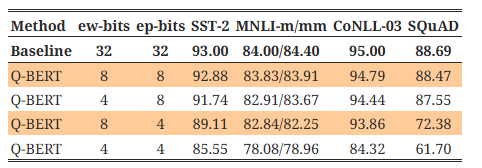

셀프 어텐션 레이어와 완전 연결 네트워크에서의 양자화 효과를 연구하기 위해, 인코더 레이어에 대해 다양한 비트 설정을 적용하여 광범위한 실험을 수행했습니다. 결과는 표 3b에 나와 있습니다. 구체적으로, 표 1d의 Q-BERTMP 설정을 채택하여 인코더 가중치에 2비트와 3비트를 혼합하여 사용했습니다. 각 인코더 레이어 내 두 모듈의 강건성을 테스트하기 위해, 해당 모듈의 비트를 하나 더 줄여 1/2MP 정밀도 설정으로 표시했습니다. 표 3b에서 볼 수 있듯이, 일반적으로 셀프 어텐션 레이어가 완전 연결 네트워크보다 양자화에 더 강건함을 확인할 수 있습니다. 1/2MP 셀프 어텐션의 경우 성능 저하가 약 7%에 그치는 반면, 1/2MP 완전 연결 네트워크에서는 성능 저하가 11%까지 악화됩니다.
5.2 질적 분석
우리는 주의(attention) 정보를 사용하여 Q-BERT와 DirectQ 간의 차이를 질적으로 분석했습니다.
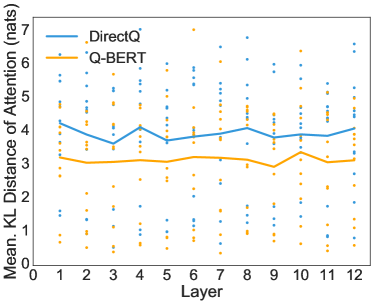
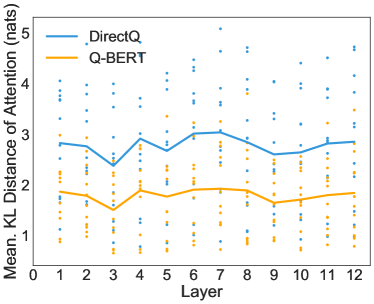
이를 위해, 양자화된 BERT와 완전 정밀 BERT의 동일한 입력에 대해 각 헤드의 주의 분포 간에 Kullback–Leibler (KL) 발산을 계산했습니다. 전체 훈련 데이터의 10%에서 평균 거리를 계산한 점에 유의해야 합니다. KL 발산이 작을수록 두 모델의 다중 헤드 주의 출력이 더 유사함을 의미합니다. 우리는 SST-2, MNLI, CoNLL-03, SQuAD에 대해 각 개별 헤드에 대한 이 거리 점수를 그림 5에 표시했습니다. Q-BERT와 DirectQ를 가중치 4비트, 임베딩 8비트, 활성화 8비트로 비교했습니다. 그림 5에서 각 점은 하나의 헤드에 대한 거리를 나타내며, 라인 차트는 한 레이어의 12개 헤드에 대한 평균 결과를 보여줍니다. 모든 레이어에서 Q-BERT가 항상 DirectQ 모델에 비해 원래 기준 모델과의 거리가 더 작음을 명확히 확인할 수 있습니다.

(a)SST-2
(b)MNLI

(c)CoNLL-03
(d)SQuAD
그림 5: Q-BERT/DirectQ와 Baseline 간의 주의 분포에 대한 KL 발산. Q-BERT와 Baseline 간의 거리는 DirectQ와 Baseline 간의 거리보다 훨씬 작습니다.
6. 결론
본 연구에서는 미세 조정된 BERT에 대한 광범위한 분석을 수행하고 BERT 양자화를 위한 효과적인 기법인 Q-BERT를 제안했습니다. 혼합 정밀도 양자화를 통해 모델 크기를 공격적으로 줄이기 위해 고유값의 평균과 분산을 모두 포착하는 새로운 레이어별 Hessian 기반 방법을 제안했습니다. 또한, 각 인코더 레이어 내부에서 세밀한 양자화를 수행하기 위한 새로운 그룹별 양자화를 제안했습니다. 네 가지 하위 작업에서 이와 같은 방법을 적용한 Q-BERT는 가중치에서 13배, 활성화 크기에서 4배, 임베딩 크기에서 4배의 압축률을 달성하면서도 성능 저하를 최대 2.3% 이내로 유지했습니다. Q-BERT에서 성능과 모델 압축률 간의 균형에 영향을 미치는 요인을 더 잘 이해하기 위해, 우리는 다양한 양자화 방식과 BERT 내의 다양한 모듈 양자화 효과를 각각 조사하는 통제 실험을 수행했습니다.
감사의 글
Prof. Joseph Gonzalez, Prof. Dan Klein, Prof. David Patterson에게 귀중한 피드백을 제공해 주셔서 감사드립니다. 본 연구는 Intel Corporation, Berkeley Deep Drive(BDD), Berkeley AI Research(BAIR)의 지원을 받아 수행되었습니다. Intel VLAB 팀이 컴퓨팅 클러스터에 대한 접근을 제공해 주신 것에 대해 감사드리며, Google의 클라우드 컴퓨팅 지원에도 감사드립니다. MWM은 ARO, DARPA, NSF, ONR, Intel의 부분적 지원에도 감사를 표합니다.

부록 A: 상세한 양자화 과정
순방향 전파에서, 가중치 또는 활성화 텐서 X의 각 요소는 다음과 같이 양자화됩니다:

부록 B: 데이터셋
Q-BERT를 감성 분류, 자연어 추론, 개체명 인식, 기계 독해 작업에 적용했습니다. 감성 분류에서는 Stanford Sentiment Treebank (SST-2) [26]를 평가하였고, 개체명 인식(NER)에서는 CoNLL-2003 영어 벤치마크 데이터셋(CoNLL-03) [25]을 사용했습니다. 자연어 추론에서는 Multi-Genre Natural Language Inference (MNLI) [34]를 테스트했으며, 기계 독해에서는 Stanford Question Answering Dataset (SQuAD) [23]에서 평가를 진행했습니다.
더 구체적으로, SST-2는 영화 리뷰 데이터셋으로, 긍정과 부정을 나타내는 이진 레이블이 포함되어 있습니다. MNLI는 다양한 장르의 자연어 추론(NLI) 작업으로, 주어진 전제-가설 쌍이 함의(entailment), 모순(contradiction) 또는 중립(neutral)인지 예측하는 과제입니다. 테스트 및 개발 데이터셋은 도메인 내(MNLI-m) 및 도메인 간(MNLI-mm)으로 나누어져 모델의 일반성을 평가합니다. CoNLL-03은 뉴스 기사 데이터셋으로, 사람, 장소, 조직, 기타 네 가지 엔터티 유형의 정확한 범위를 예측하는 과제입니다. SQuAD는 각 샘플에 주어진 문맥 단락과 질문을 바탕으로 문맥에서 관련 범위를 추출하여 답변을 찾는 과제입니다.
부록 C: 추가 결과
여기에서는 몇 가지 추가 결과를 설명합니다.
C.1 헤시안 기반 혼합 정밀도 할당의 소거 연구
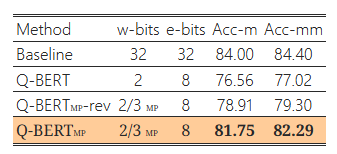
헤시안 기반 혼합 정밀도 방법의 효과를 입증하기 위해, 2/3비트 Q-BERTMP의 반대 버전(Q-BERTMP-rev)을 사용하는 소거 연구를 진행했습니다. 구체적으로, 민감도가 상대적으로 높은 레이어에는 낮은 비트를, 민감도가 낮은 레이어에는 높은 비트를 할당하여 모델 크기는 동일하게 유지합니다. 이는 2/3비트 Q-BERTMP에서 2비트를 할당한 이전 레이어가 Q-BERTMP-rev에서는 3비트를 할당받는 것을 의미합니다.7
7 2/3비트 Q-BERTMP 및 2/4비트 Q-BERTMP의 비트 설정은 각각 표 6과 표 7에 포함되어 있습니다.
동일한 모델 크기에서 Q-BERTMP-rev와 2비트 Q-BERT의 성능 차이는 MNLI, CoNLL-03, SQuAD에서 2% 이내, SST-2에서는 4% 이내로 나타났습니다. 반면, Q-BERTMP의 성능 차이는 MNLI, CoNLL-03, SQuAD에서 5% 이상, SST-2에서는 8% 이상이었습니다. 이러한 큰 성능 차이는 혼합 정밀도 비트 할당에서 2차 헤시안 정보를 활용하는 것의 우수성을 보여줍니다.
표 4: 반전된 헤시안 기반 혼합 정밀도 설정에 대한 양자화 결과. Q-BERTMP와 반대 비트 할당을 사용한 모델을 Q-BERTMP-rev로 나타냅니다.

(a)SST-2
(b)MNLI
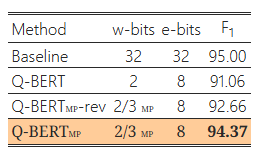
(c)CoNLL-03
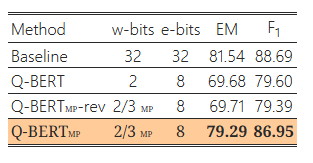
(d)SQuAD
C.2 임베딩에 대한 혼합 정밀도 양자화
표 1d에서 볼 수 있듯이, 2/3 MP를 가중치 파라미터에 적용할 때 모델 크기의 병목은 임베딩 테이블 크기에 의해 제한됩니다. 또한, 표 3a에서 단어 임베딩이 덜 민감하다는 것을 확인했습니다. 따라서, 이 절에서는 전체 모델 크기를 줄이기 위해 임베딩 테이블을 4비트(단어 임베딩)와 8비트(위치 임베딩) 혼합 정밀도로 설정했습니다. 가중치에 대한 그룹별 양자화와 유사하게, 초저비트 임베딩 설정에서는 BERTBASE의 단어 및 위치 임베딩 레이어에서 768개 출력 뉴런을 표 5에서 128개의 그룹으로 묶었습니다. 우리는 가중치와 활성화에 대해 표 1d와 동일한 설정을 채택했으며, 여기서 가중치는 128개 그룹으로 설정하고 활성화는 8비트를 사용했습니다. 약 0.5%의 성능 저하와 함께 임베딩 테이블 크기는 11.6MB로 줄일 수 있으며, 이는 임베딩 테이블에서 약 8배, 전체 모델 크기에서 약 12배의 압축률에 해당합니다.
표 5: Q-BERT의 네 가지 작업에 대한 임베딩 혼합 정밀도 양자화 결과. 각 인코더 레이어와 임베딩 레이어에서 128개의 그룹을 사용하여 결과를 얻었습니다. 가중치에 사용된 양자화 비트는 "w-bits", 임베딩은 "e-bits", 모델 크기(MB 단위)는 "Size", 임베딩 레이어를 제외한 모델 크기(MB 단위)는 "Size-w/o-e"로 나타냈습니다. 단순성과 효율성을 위해 기준 모델을 제외한 모든 모델은 8비트 활성화를 사용했습니다. 여기서 "MP"는 혼합 정밀도 양자화를 의미합니다. 혼합 정밀도 임베딩은 4비트 단어 임베딩과 8비트 위치 임베딩을 사용했습니다.

(a)SST-2

(b)MNLI

(c)CoNLL-03

(d)SQuAD
C.3 SST-2에 대한 상세한 손실 지형 분석
SST-2 작업에 대한 상세한 손실 지형 분석을 그림 6에 포함했습니다.

(a)SST-2 3th layer
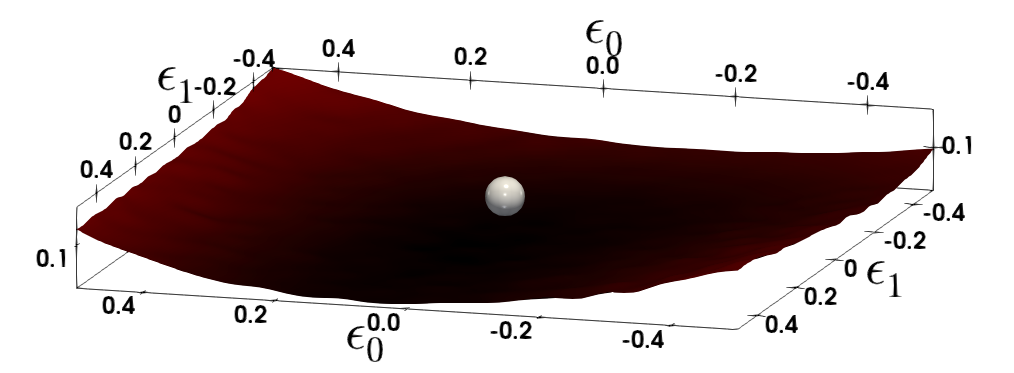
(b)SST-2 10th layer
그림 6: SST-2의 다양한 레이어에 대한 손실 지형은 Hessian의 첫 두 주요 고유벡터를 따라 파라미터를 변동시키면서 시각화했습니다. 은색 구체는 BERT 모델이 수렴한 파라미터 공간의 지점을 나타냅니다.
표 6: 모든 네 가지 작업에서 2/3비트 Q-BERTMP에 대한 비트 설정.
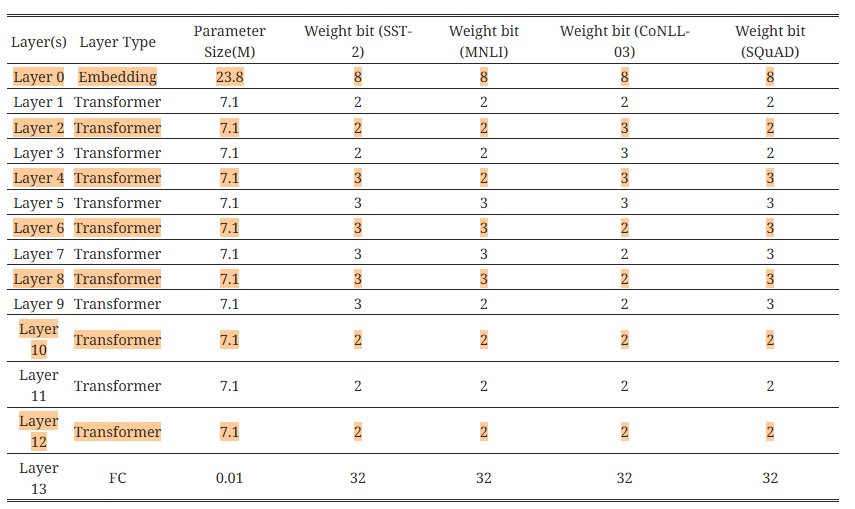
표 7: 모든 네 가지 작업에서 2/4비트 Q-BERTMP에 대한 비트 설정.




