Goal of Machine Learning
통상적으로 기계 학습(機械學習) 또는 머신 러닝(영어: machine learning)은 경험을 통해 자동으로 개선하는 컴퓨터 알고리즘의 연구로 정의한다.
결국, 해당 정의는 주어진 데이터를 가장 잘 설명하는 함수를 찾아라라는 의미이다.
예를 들어보자.
주어진 데이터를 다음 그림으로 정의하겠다.

이에 최적화된 함수를 찾기위해서는 어떻게 해야될까?
여러종류의 모델중에서 선택하면 된다!
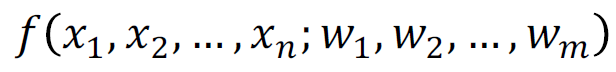
임의의 함수 f에서 주어진 데이터에 가장 잘 부합도록 변수들을 조정하는 것이다.
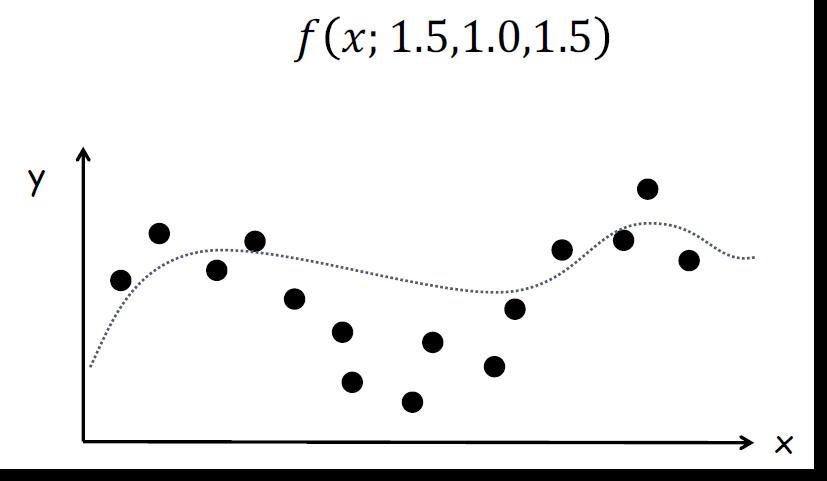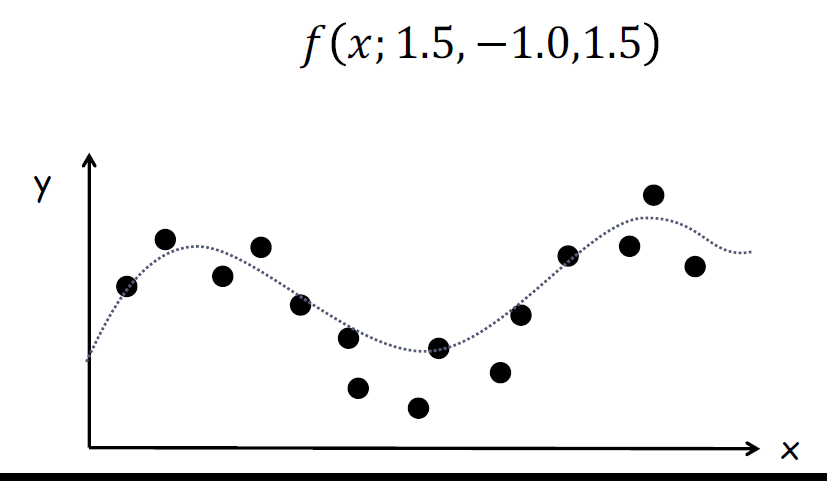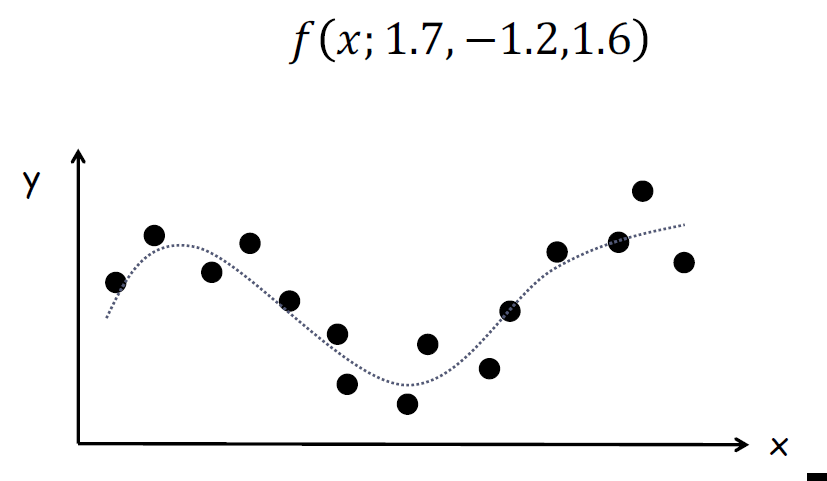
마지막으로 결정된 함수를 이용하여 값을 예측하면 이것이 machine learning이다.
하지만 여기에도 문제점들이 있다.
주어진 데이터를 가장 잘 설명하는 함수를 찾아라에서 우리는 어떻게 가장 잘 설명하는 함수를 찾는가가 문제다.
앞에서 해두고 이게 무슨 말인가 할 수 있다. 예시를 이미 보여주었는데!
앞서한 예제들은 함수를 찾는 방법에 대한 설명이고 가장 잘 설명하는 함수를 찾은것은 아니기 때문이다!
주어진 데이터를 가장 잘 설명하는 함수란? 오류를 최소화하는 함수이다.

이 그래프에서 오류를 최소화하는 함수를 구하기 위해서는 Error를 최소화하면된다.
-> 함수모양은 𝑤1 ,𝑤2 ,…,𝑤m 가 결정하기 때문!
Error 함수를 최소화하는 함수는 Error를 최소화하는 𝑤1 ,𝑤2 ,…,𝑤m를 찾는 것이다.
이를 요약하면 다음과 같다.

그렇다면 이 문제는 어떻게 풀어야할까?
결국, 위의 말은 E를 모든 𝑤i들에 대해서 편미분을 하고, 이것을 모두 0으로 만드는 모든 𝑤i를 찾으면 된다는 것이다!

이에 관련된 문제를 풀어보도록 하자!
Data = {(0,0), (1,1), (1,2), (2,1)}
f(x; w0, w1, w2) = w2x2 + w1x +w0일 때의 최적의 함수를 구하라.

하지만 위의 문제의 답은 항상 존재할까?
일반적으로 알려진 방정식의 풀이는 갈루아에의하여 5차 이상의 고차 방정식에는 사칙연산, 거듭제곱을 이용한 근의 공식이 없다는 것이 증명되었다.
그렇다면 답이 없는 문제는 어떻게 풀어야할까?
문제를 조금 바꿔보면 된다!

이렇게 말이다.

위의 함수를 풀기위해서는 어떻게해야될까?
경사면을 따라 내려가면 되지 않을까?
이 방법이 바로 모든 머신 러닝에서 일반적으로 사용되는 Gradient Descent Method이다.
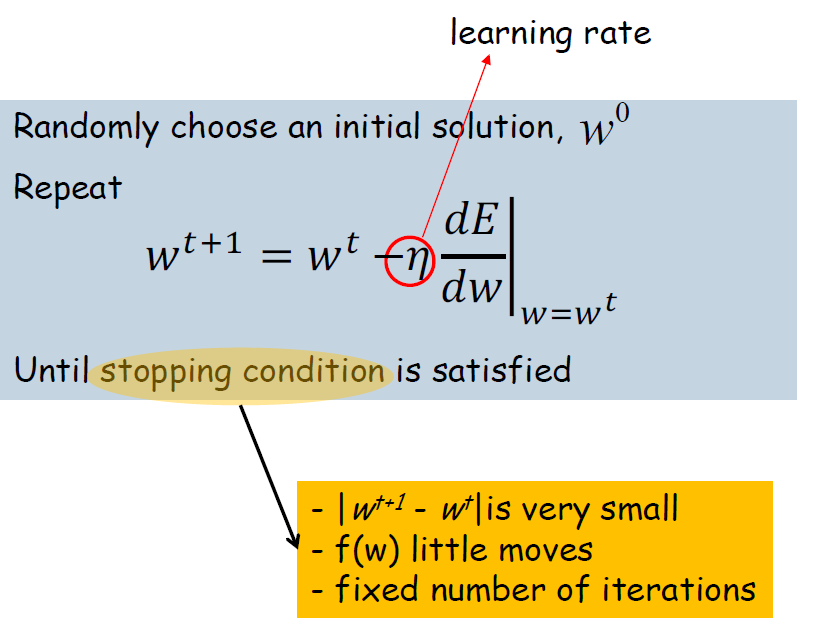
위의 공식을 사용해서 경사하강법을 사용할건데 수식을 보면 상당히 어려워 보이지만 이를 실제 적용한 걸 보면 직관적으로 이해 가능할 것이다.

Gradient Descent Method 적용은 다음의 순서를 따른다.
1. Random하게 임의의 시작점을 잡는다.
2. 현재 위치에서 미분 가능하기 때문에, 미분을 통해 경사를 구하고 이를 내려가기 위해 기울기의 반대 방향으로 적용한다.
3. 해당 방향으로 조금 이동한다. -> 너무 큰 스탭으로 이동하면 minimize된 지점을 건너뛸수 있기 때문이다.
4. 기울기가 0인 곳에 도달할 때까지 3을 계속하기
Gradient Descent Method 공식을 다차원인 경우는 각 변수에 대해서 진행해야함으로 다음의 식이 된다.

앞에서 풀었던 문제를 위와 같이 풀면 다음과 같다.
Data = {(0,0), (1,1), (1,2), (2,1)}
f(x; w0, w1, w2) = w2x2 + w1x +w0일 때의 최적의 함수를 구하라.
수식으로는 앞에서 풀었기 때문에 이를 파이썬으로 구현했다.
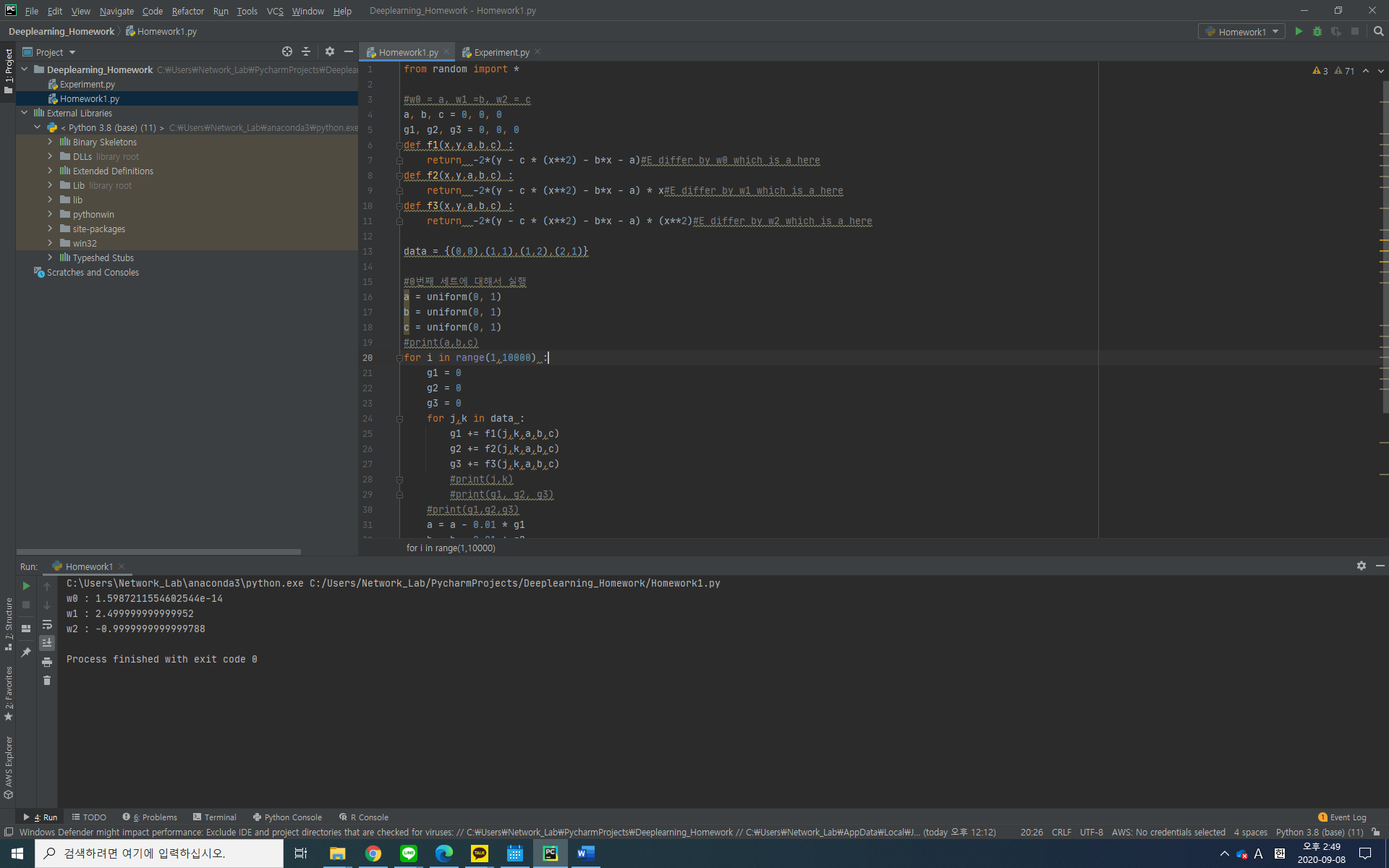
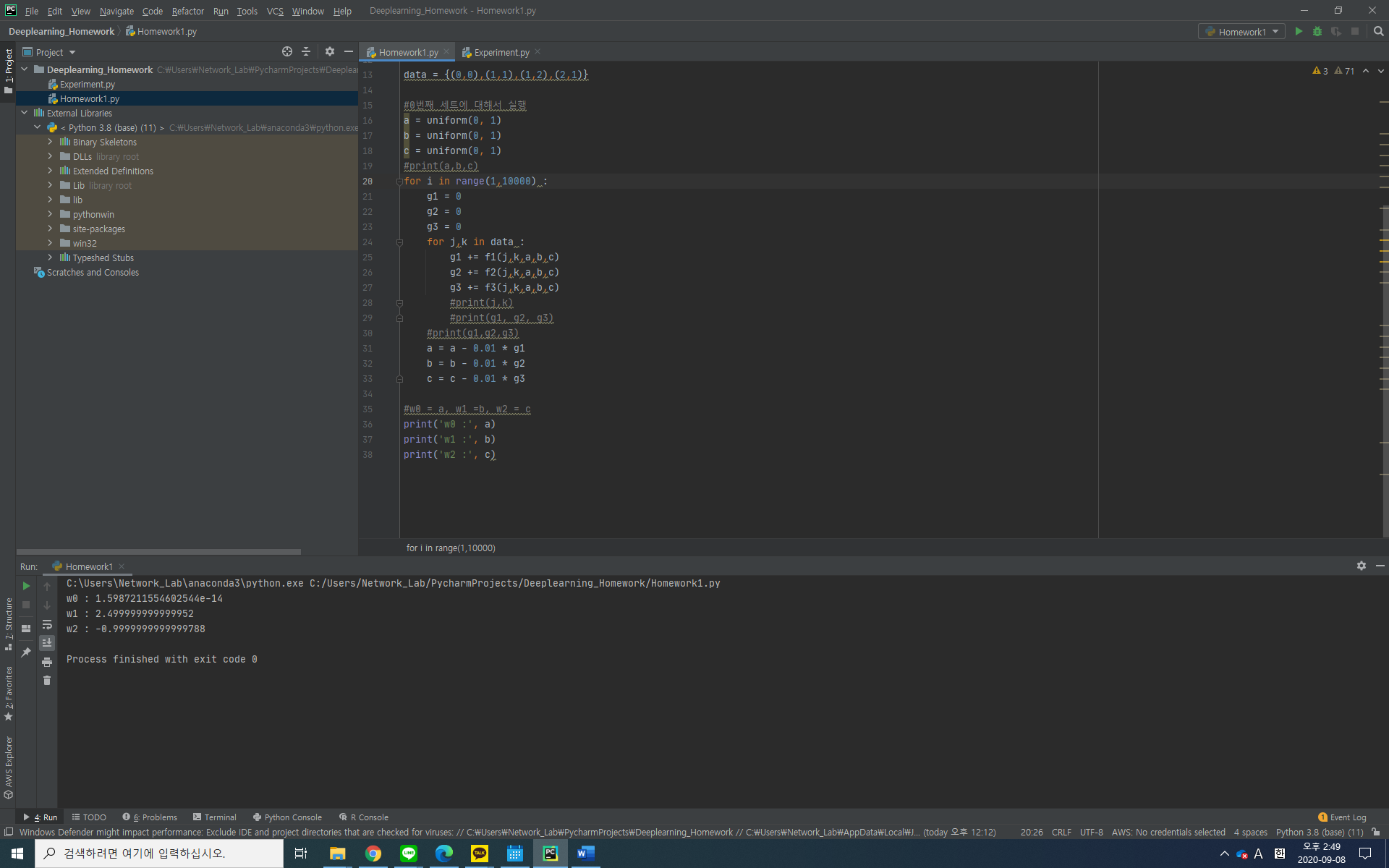
'인공지능' 카테고리의 다른 글
| Chapter 4 CNN Structures (1) | 2023.05.19 |
|---|---|
| Diffusion Model (0) | 2023.04.01 |
| Chapter 3 Convolutional Neural Networks (0) | 2023.02.13 |
| Chapter 2-2 Neural Networks (0) | 2023.02.05 |
| Chapter 2-1 Neural Networks (0) | 2023.01.27 |



