Chapter2 초기를 상기해보자. 우리는 Shallow Network와 Deep Network의 정의를 하고 넘어갔다.
이론적으로 Shallow Networks는 모든 기능을 모방할 수 있지만, 노드 수가 기하급수적으로 증가할 수 있다. 이런 기하급수적 노드의 폭발을 피하기 위해 Deep Network를 채택하고 있다. 하지만 Deep Network는 매우 강력한 힘을 가지고 있지만 많은 문제점들이 존재한다. 대표적인 예로는 어려운 최적화, Overfitting, Internal covariate shift가 있다.
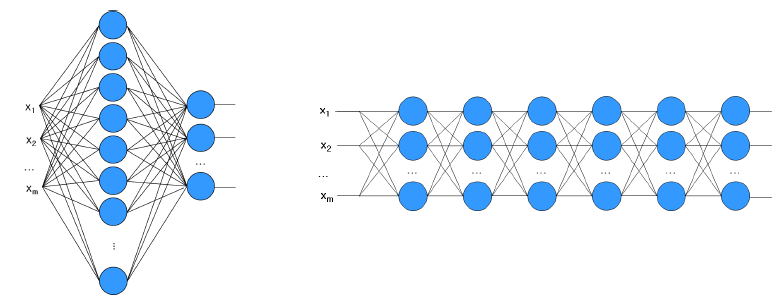
많은 노드들이 사용이된다면 많은 항이 곱해지며 연산이 많아지게 된다. 그 여파로 인하여, 일부 값들이 작은 경우 기울기가 전체적으로 매우 작아며 반대로 일부 값들이 큰 경우 기울기가 전체적으로 매우 커진다. 이는 다음의 그림을 보면 확인할 수 있다.
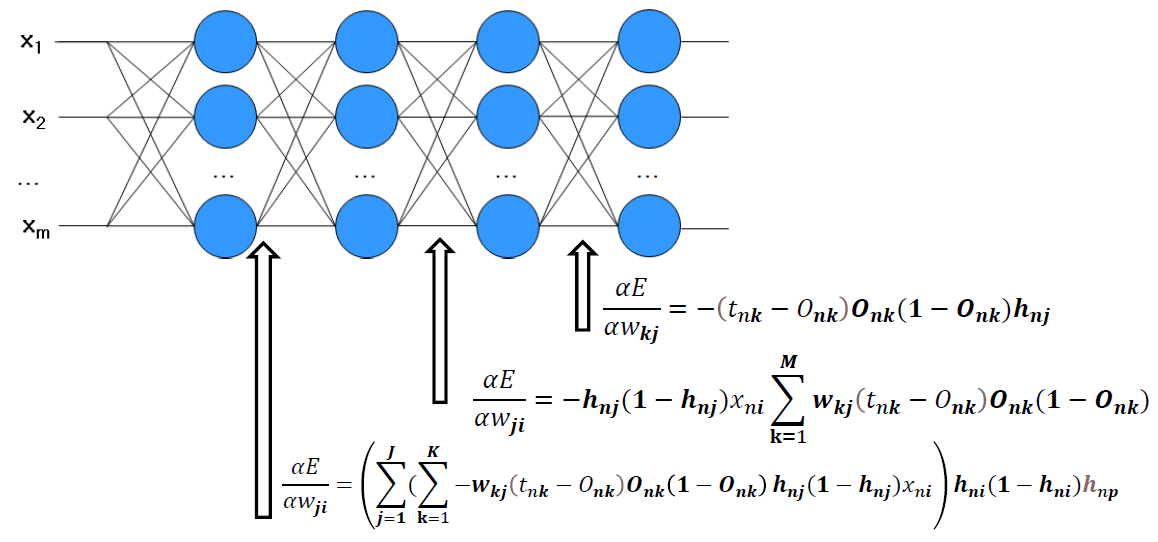
그림에서 나타난 식(chapter2-1에서 더보기에서 수식을 설명했다.)에 문제점이 무엇일까?
Onk가 바로 sigmoid 함수라는 것이다.

이는 2가지의 문제점을 야기할 수 있다.
Vanishing Gradient Problem과 Saturation Problem이다.
Vanishing Gradient Problem: Sigmoid 함수의 기울기는 0에 가까워질수록 점점 작아고 이는 Onk(1-Onk)가 0이 된다는 뜻으로 깊은 네트워크에서 학습이 잘 이루어지지 않게 된다다.
Saturation Problem: Sigmoid 함수의 기울기는 1또는 0에 가까워질수록 점점 작아고 이는 Activation function 값이 1 또는 0이 된다는 뜻으로 이는 각 뉴런의 출력이 일정한 값으로 수렴하는 현상을 일으킨다.
조금 더 수식적으로 생각해보면 아래와 같다.
Vanishing Gradient Problem: Onk(1-Onk) => 작은 값으로 수렴하게 되기 때문에, 깊은 네트워크에서의 Onk(1-Onk)값이 0으로 수렴되는것과 같은 현상을 보인다.
Saturation Problem: Output 값 => 1 or 0으로 수렴하면 각 뉴런의 출력이 일정한 값인 경우는 sigmoid 자체가 상수 값으로 대체되기 때문에 미분시 항상 0으로되어 문제를 발생한다.
이런 문제들을 Activation Function의 변화를 주면 해결 되는 놀라운 일이 발생한다.
Sigmoid function을 Rectified Linear Unit(Relu) function으로 변경하면 된다!
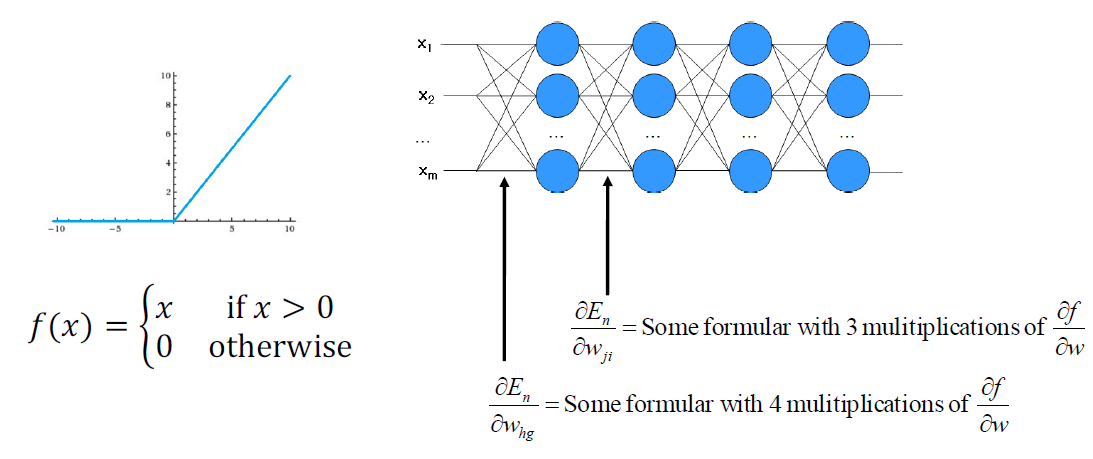
Relu를 사용하면 다음의 장점들이 있다.
– Vanishing gradient problem이 사라진다.
– Sparse activation
• 무작위로 초기화된 네트워크에서는 hidden units의 약 50%만 활성화됨(꼭 알필요는 없다.)
– Fast computation
• Sigmoid function보다 6배 빠름
반대로 단점 또한 존재한다.
Knockout Problem로 이는 단일 뉴런 또는 뉴런 그룹이 훈련 중에 네트워크에서 제거되거나 "녹아웃"되는 인공 신경망의 상황이다. 이는 과적합, 잘못된 가중치 초기화 또는 훈련 데이터 부족과 같은 다양한 이유로 인해 발생할 수 있다. 녹아웃의 결과는 네트워크의 성능이 저하되고 새로운 데이터에 잘 일반화되지 않을 수 있다는 것이다. 녹아웃 문제를 피하려면 드롭아웃, 가중치 감쇠 또는 조기 중지와 같은 정규화 기술을 사용하여 오버피팅을 방지하고 네트워크의 일반화를 개선하는 것이 중요하다.
추가적으로 ReLU units은 다음과 같은 상황에서 처할수 있다.
– 모든 데이터 포인트에 대해 노드가 실행되지 않는 경우(항상 음수) -> 훈련되지 않음(Backpropagation이 작동하지 않기 때문에)
– ReLU를 통해 흐르는 큰 그래디언트의 경우 가중치를 크게 업데이트함
– 가중치는 뉴런이 어떤 데이터 포인트에서도 다시 활성화되지 않는 매우 나쁜 지점에 위치할 수 있음
– 학습률이 너무 높게 설정되면 네트워크의 최대 40%가 활성화되지 않을 수 있음
위의 경우는 자주 일어나지는 않지만 이를 피하기 위해서 고안된 함수로 Leaky Relu가 존재한다.

Leaky Relu는 값이 음수여도 0.01의 값이 존재하여 훈련되지 않는 경우를 방지할 수 있다.
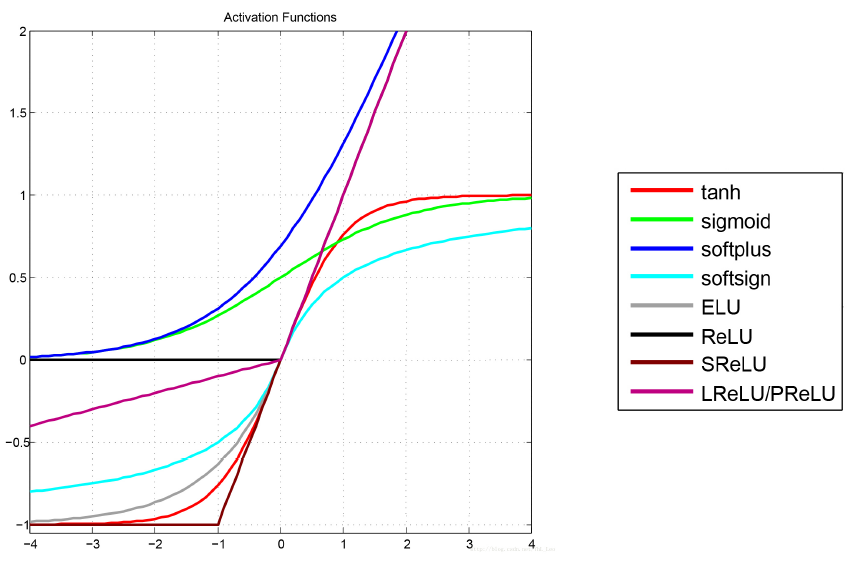
이미 내용을 알고 있는 사람이면 아래의 요약을 보시면 된다.
– Sigmoid 함수와 그 조합은 일반적으로 더 잘 작동하지만 기울기 소실 문제로 인해 때때로 사용하지 않는 경우가 있음
– ReLU 기능은 일반적인 활성화 기능으로 요즘 대부분의 Neural Network에서 사용됨
– 네트워크에서 죽은 뉴런의 경우가 발생하면 Leaky ReLU를 사용하는 또 다른 선택지가 있음
– ReLU 기능은 일반적으로 Hidden layer에서 사용되며 Output에서의 activation function은 우리가 상황에 맞게 정해야함
– 일반적으로 ReLU 기능을 사용하여 시작한 다음 ReLU가 최적의 결과를 제공하지 않는 경우 다른 활성화 기능으로 변경하는게 좋음
이번에는 Ch2-1에서 배웠던 Overfitting(과적합)을 방지하는 법에 대해서 알아보자.
Regularization, Early stopping, Max norm constraints, Weight decay, Dropout, DropConnect, Stochastic pooling 등이 있다.
Regularization은 Overfitting 방지를 위한 정보를 추가하는 방법이다.
Early Stopping은 많이 수렴하기 전에 학습을 중지하는 방법이지만, 일반적으로 유효성 검사 데이터 세트에 의해 결정되며 학습을 멈출 시간을 결정하기 어렵다는 단점이 있다.
Max norm constraints은 주어진 상수 c 이상으로 성장하지 않도록 가중치 벡터 적용하는 방식으로 상수가 c 이상 자라면 상수는 c로 결정된다.
Weight Decay는 L1 Regularization과 L2 Regularization으로 구성되어있으며, 머신러닝을 공부해본 사람은 친숙할 것이다.
- L1 Regularization: 대부분의 가중치를 0에 매우 가깝게 유도하여 가장 중요한 입력의 작은 하위 집합 선택시킨다. 따라서 입력의 노이즈에 강하다.
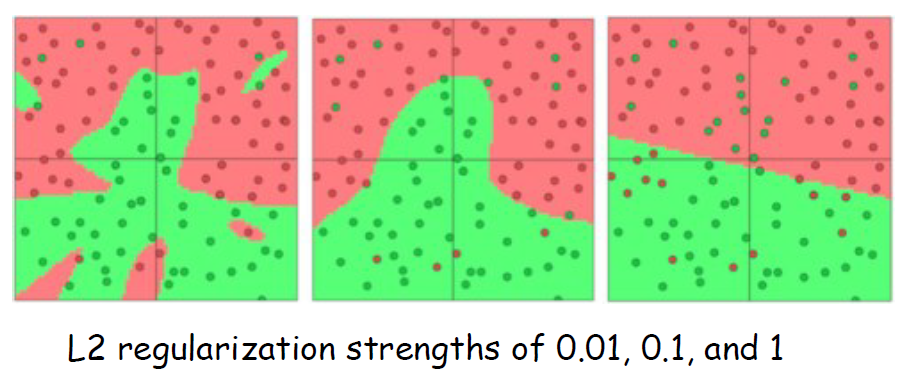
- L2 Regularization: 최고 중량에 페널티 부여하며 입력의 일부만 많이 사용하기보다는 모든 입력을 조금씩 사용하도록 권장한다.
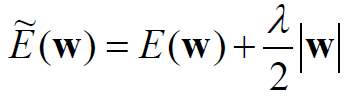
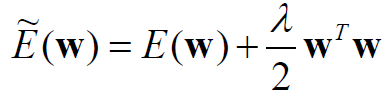
추가적인 L1과 L2의 차이점을 알고싶으면 다음을 참고하라.(https://light-tree.tistory.com/125)
Dropout은 가장 핵심적인 내용이며 나중에 사용할 수도 있고 안할 수도 있지만, 무조건 알고 있어야하는 개념이다. 중요한 내용임으로 하나씩 살펴보도록하자. Complex Neural Network에서는 모든 노드가 동일한 책임을 지지 않음기 때문에 모든 노드가 동일하게 훈련되지 않는다. 즉, 일부 노드는 많이 훈련되지만 일부는 그렇지 않는다. 그렇게 발생하는 것이 노드의 출력이 불량한 경우, connection weight이 감소되며 연결 가중치가 0에 가까우면 선행 connection weights는 거의 훈련되지 않는다. 극단적으로 아래의 그림처럼 1개의 노드쪽으로 Training이 쏠릴 수 있다는 것이다.
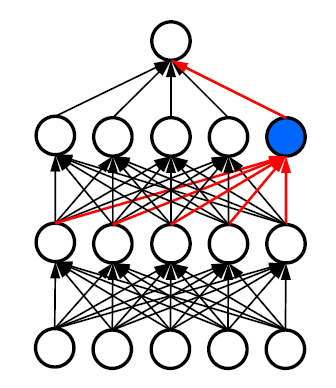
그렇다면 구조적 복잡성에 따라 안좋은 결과를 나타내니 이를 줄이면 되지 않을까?
그렇게 생각하게 된다면 일부 노드를 제거하고 단순화된 신경망 훈련시키고 이를 합치면 되지 않을까?
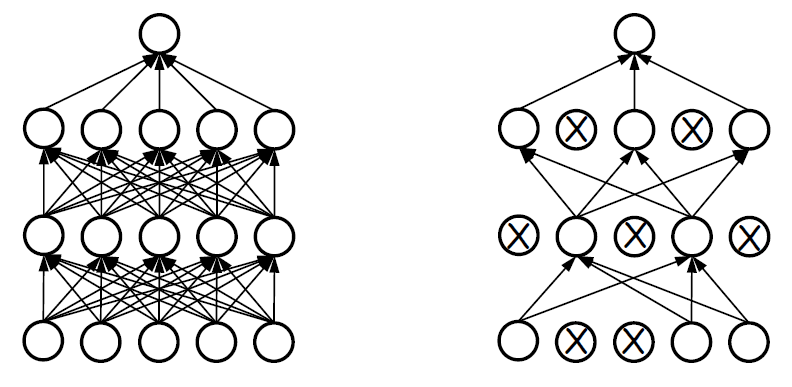
그렇다면 공정성을 위해서 확률이 p(일반적으로 p = 0.5)인 노드를 무작위로 선택하고, 이를 통해 만들어진 단순화된 신경망 훈련을 반복시키면 신경망과 노드들이 골고루 학습된다. 인공지능 분야에서는 반복을 샘할때, epoch이라는 단위를 사용한다. 우리가 생각한 것을 반영시키면 다음과 같이 학습이 진행될 것이다.
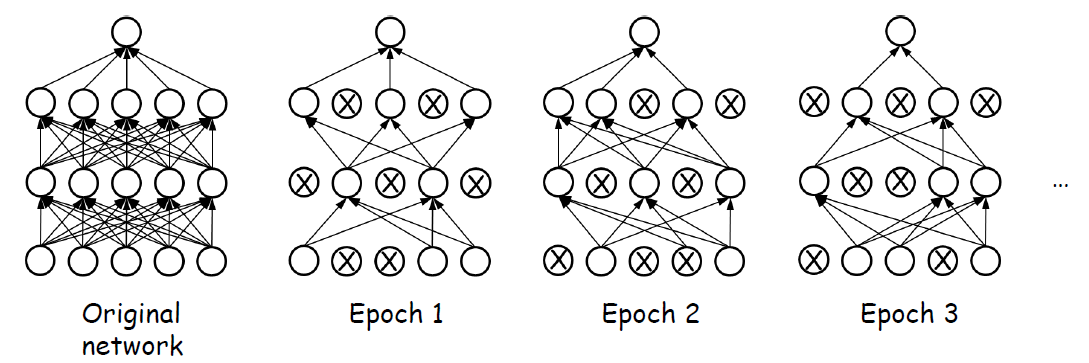
결국 이를 학습시킨다해도 결론적으로는 학습된 결과를 합치고 테스트도 해야한다. 어떻게 하면 될까?
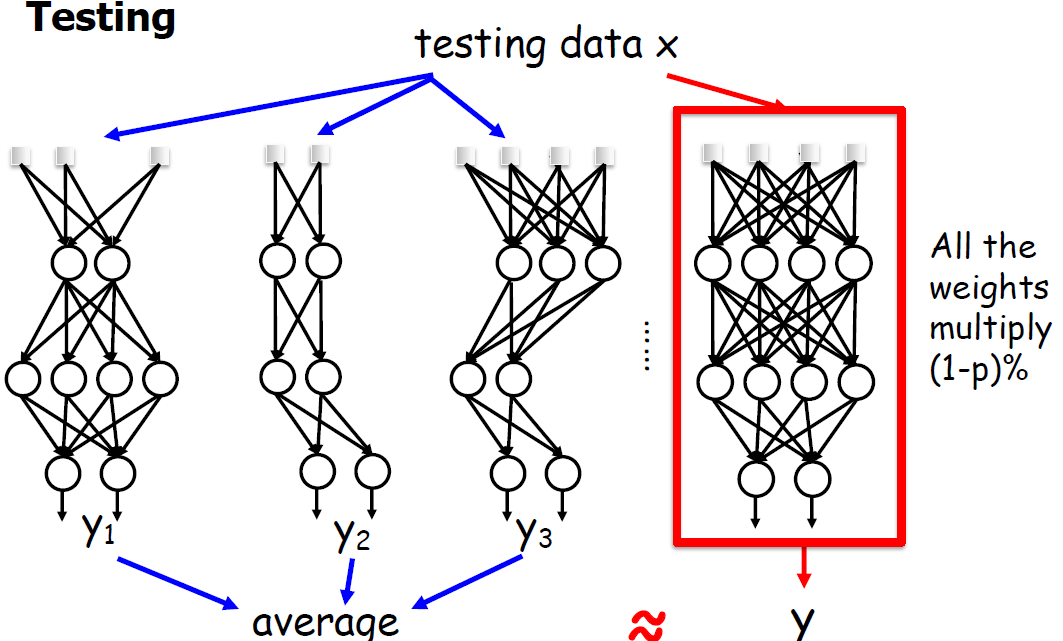
테스트 중에 뉴런을 임의로 삭제하는 대신 모든 뉴런이 활성 상태로 유지되고 해당 출력이 드롭아웃 비율과 동일한 요소로 조정한다. 이를 통해 네트워크의 활성화가 교육 중 활성화와 일치하는 동시에 드롭아웃 효과도 고려하는 것이다. 그런 다음 네트워크의 최종 출력은 각각 다른 드롭아웃 구성을 가진 여러 순방향 패스의 평균으로 계산되며, 이를 통해 네트워크 출력의 분산을 줄이고 테스트 중에 보다 강력한 결과를 제공할 수 있다.
결론적으로 아래의 그림을 설명한 것과 같다.
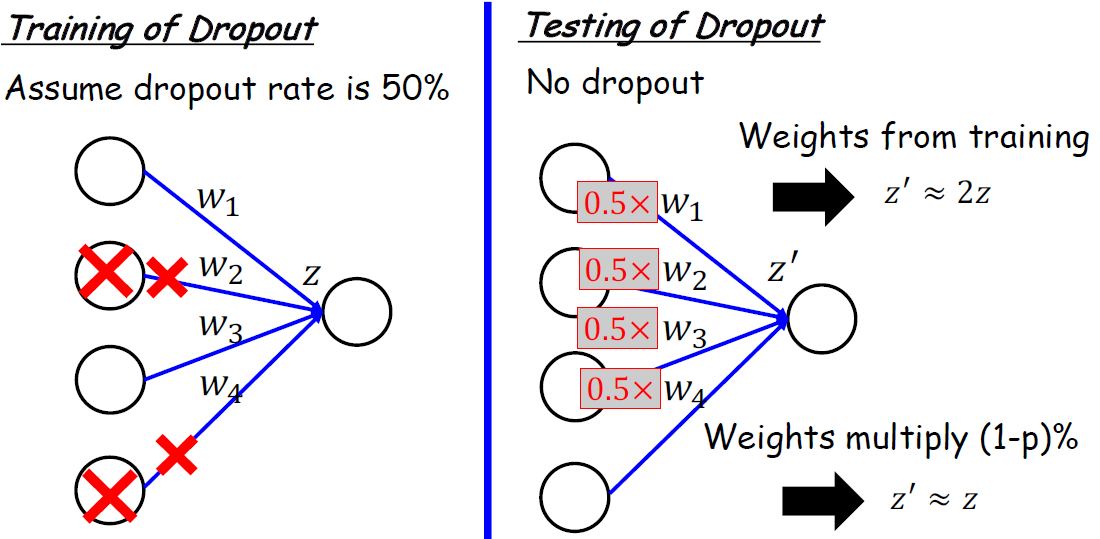
조금 더 상세한 Traing 그림을 원하면 더보기를 보면 된다.
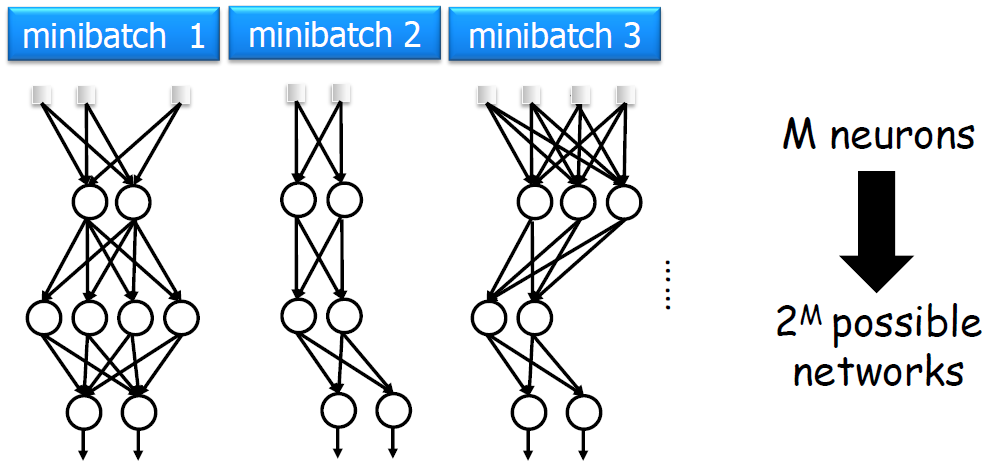
Dropout의 효과를 784-2048-2048-2048-10 구조의 Nerual Network를 MNIST dataset에서 비교한 결과이다.
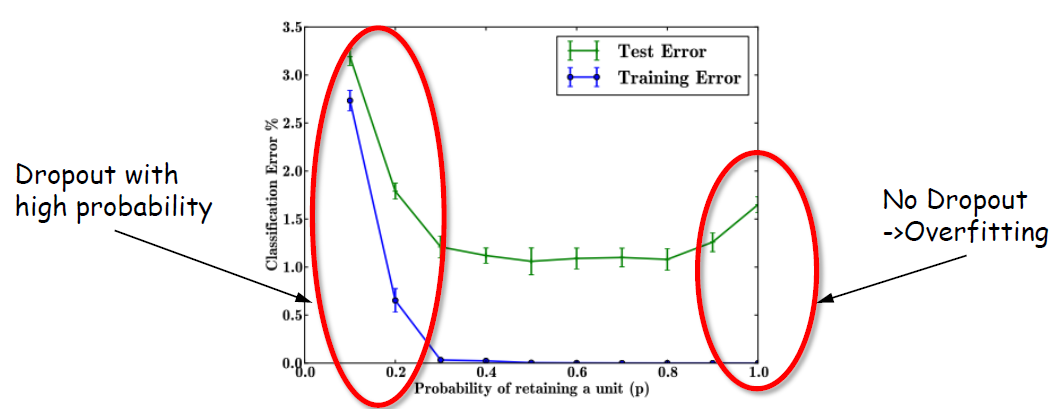
확연히 Dropout에서 overfitting이 이러나지 않는 것을 알 수 있다.
그렇다면 data set 크기에서 비교하면 어떨까?
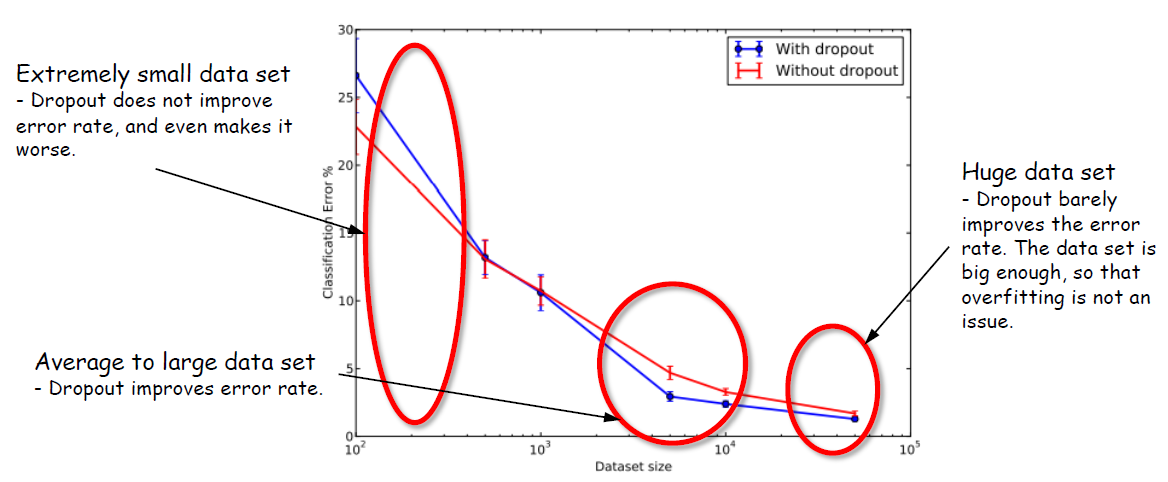
매우 작은 데이터 세트 : 드롭아웃은 오류율을 개선하지 않으며 오히려 악화시킨다.
평균에서 대용량 데이터 세트: Dropout으로 에러율이 개선되었다.
거대한 데이터 세트: 드롭아웃은 오류율을 거의 개선하지 못했다. 데이터 세트가 충분히 크므로 과적합이 문제가 되지 않게 된 것이다. 이는 Regularization이 사용된 것과 같은 효과를 보았기 때문이다.
간단히 요약하면, Dropout은 매우 훌륭하고 빠른 정규화 방법이지만, 훈련시간이 많이 필요하며 (Dropout이 없는 것보다 2-3배 느림) 데이터의 양이 평균적으로 많은 경우 드롭아웃이 우수하다. 일반적으로 알려져있기로는 Weight Decay보다 더 좋은 결과를 얻을 수 있는 것으로 알려져있다.
훈련 중에 네트워크의 활성화 분포가 변경될 때 발생하는 내부 공변량 이동 문제를 Covariate Shift라 한다. 간단하게 설명하면 함수 영역 분포의 변화가 생긴다는 말이다. 이런 변화는 우리가 학습시킨 모델을 제대로 작동할 수 없는 환경을 만든다.
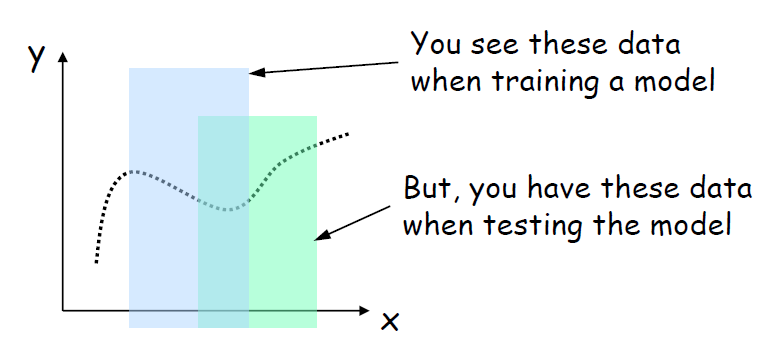
훈련 중에 신경망 계층에 대한 입력 분포가 변경되는 현상을 Internal Covariate Shift라고 하며, 이전 레이어의 매개변수가 업데이트되어 이후 레이어가 받는 활성화 분포의 변화로 인해 발생할 수 있다. 이러한 변화는 훈련 속도를 늦추고 네트워크가 학습하는 것을 더 어렵게 만들 수 있다.
말이 어려워 보이지만 좀 더 간단하게 설명하면 한번 연결 가중치를 변경하면 레이어에 대한 입력 분포가 변경되면 상위 상위 계층으로 전파가 되어 훈련 속도를 늦추고 네트워크가 학습하는 것을 더 어렵게 만들 수 있는 것이다.
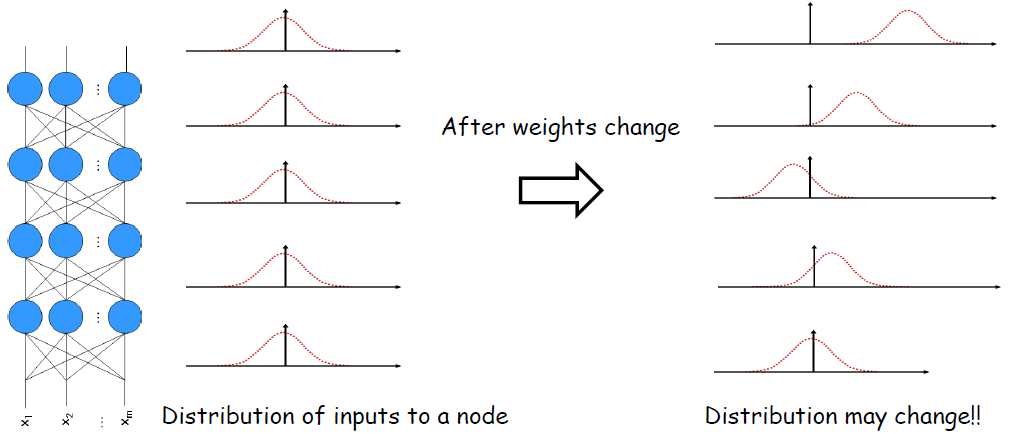

Internal Covariate Shift를 좀 더 쉽게 보면 빨강색 노드의 입력 분포가 학습하는 동안 입력 분포에 따라 빨간색 연결 가중치가 변경되며, 학습 후 전체 연결 가중치가 변경되어 입력 분포가 변경되는 것을 말한다.
따라서 Internal Covariate Shift는 학습 과정을 방해하고, 느려지게 한다. 이를 어떻게 해야 해결할 수 있을까? 입력 분포를 정규화하면 일정한 분포로 학습하기 때문에 위와 같은 문제점을 해결할 수 있지 않을까?
수학적으로 확인하고자 하면 다음의 사이트에서 확인된다.
Understanding the Math behind Batch-Normalization algorithm, part-1
Mathematics is not scary at all, its just that we need to break down things as simpler as possible to comprehend its profoundness.!
medium.com
일정한 분포로 학습하기위해 우리는 모든 노드의 입력 분포가 가우시안으로 변경하여 학습시킨다. 이를 Batch Normalization이라고 부른다.
Batch Normalization의 장단점은 다음과 같다.
장점
- 더 빠른 수렴: 배치 정규화는 입력을 정규화하여 활성화의 분산을 안정화하고 그래디언트 폭발의 위험을 줄이고 더 빠른 수렴으로 이어짐
- 개선된 정규화: 배치 정규화는 활성화에 노이즈를 추가하여 과적합을 줄이고 일반화를 개선하여 정규화 역할을 함
- 더 쉬운 하이퍼파라미터 튜닝: 배치 정규화를 사용하면 더 큰 학습 속도가 가능하므로 네트워크의 안정성에 대해 걱정할 필요가 없으므로 하이퍼파라미터 튜닝이 더 쉬워짐
- 잘못된 초기화에 대한 복원력: 배치 정규화는 네트워크에 대한 잘못된 가중치 초기화의 영향을 완화하여 가중치에 대한 좋은 시작점을 찾는 데 덜 의존하도록 할 수 있음
단점
- 복잡성 증가: 배치 정규화는 모델에 추가 계산 및 하이퍼파라미터를 추가하여 구현 및 최적화가 더 복잡해짐
- 비효율적인 계산: 정규화 프로세스는 특히 계층이 많은 심층 네트워크에서 계산 집약적일 수 있음
- 해석 가능성 감소: 배치 정규화를 사용하면 모델의 출력과 입력 변수와 출력 변수 간의 관계를 해석하기가 더 어려워질 수 있음
- 안정성 부족: 정규화 프로세스는 때때로 불안정한 활성화를 초래하여 최적이 아닌 모델 성능으로 이어질 수 있음
- 과적합: 배치 정규화는 때때로 네트워크에 많은 노이즈를 추가할 수 있으므로 더 작은 데이터 세트에 과적합될 수 있음
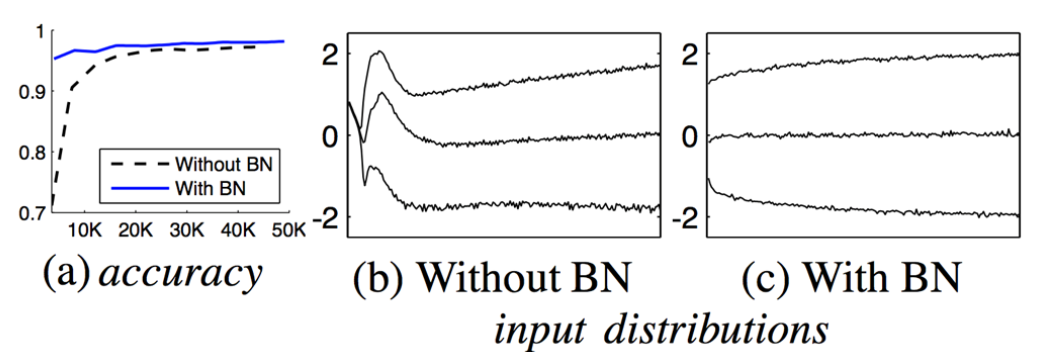
전반적으로 Batch Normalization은 Neural Network의 안정성과 성능을 개선하는 데 도움이 되는 것으로 알려져있지만, 최근 연구 추세에서는 꼭 Batch Normalization이 필수적인 것은 아니라고 한다. 다음의 글을 참고하면 좋다.
Is Batch Normalization harmful? Improving Normalizer-Free ResNets
Review the limitations of BN and an architecture without Batch Normalization
medium.com
실제로 내 경험상 Batch Normalization을 사용하는 경우, 데이터의 특성을 완전이 담아내지 못하는 학습을 하는 경우도 많이 있었다. 따라서 Batch Normalization을 사용할 때에는 조심해서 사용해야될 것이다.
여기까지 기본적인 Neural Network에서 알아야할 개념이었다. 다음 Chapter는 Deep Neural Network(심층 신경망)의 여러가지 종류들에 대해서 알아보도록하자.
'인공지능' 카테고리의 다른 글
| Chapter 4 CNN Structures (1) | 2023.05.19 |
|---|---|
| Diffusion Model (0) | 2023.04.01 |
| Chapter 3 Convolutional Neural Networks (0) | 2023.02.13 |
| Chapter 2-1 Neural Networks (0) | 2023.01.27 |
| Chapter 1 Machine Learning (1) | 2023.01.20 |



