Simplifying, Stabilizing and Scaling Continuous-Time Consistency Models

https://arxiv.org/abs/2410.11081

Simplifying, Stabilizing and Scaling Continuous-Time Consistency Models

 

요약
일관성 모델(Consistency Models, CM)은 빠른 샘플링을 위해 최적화된 확산 기반 생성 모델의 강력한 클래스입니다. 대부분의 기존 CM은 이산화된 시간 단계(discretized timesteps)를 사용하여 훈련되며, 이는 추가적인 하이퍼파라미터를 도입하고 이산화 오류에 취약해지는 문제를 일으킵니다. 반면, 연속 시간(continuous-time) 기반의 공식은 이러한 문제를 완화할 수 있지만, 훈련의 불안정성으로 인해 성공 사례가 제한적이었습니다. 이를 해결하기 위해, 우리는 확산 모델과 CM의 이전 매개변수를 통합하는 단순화된 이론적 프레임워크를 제안하며, 불안정성의 근본 원인을 식별했습니다. 이러한 분석을 바탕으로, 우리는 확산 과정의 매개변수화, 네트워크 아키텍처, 훈련 목표에 대한 중요한 개선 사항을 도입합니다. 이러한 변경을 통해 우리는 연속 시간 CM을 전례 없는 규모로 훈련할 수 있게 되었으며, ImageNet 512×512에서 15억 개의 매개변수를 다루는 모델을 성공적으로 구현했습니다. 우리의 제안된 훈련 알고리즘은 단 두 번의 샘플링 단계만으로 CIFAR-10에서 FID 점수 2.06, ImageNet 64×64에서 1.48, ImageNet 512×512에서 1.88을 기록하였으며, 기존 최상의 확산 모델과의 FID 점수 차이를 10% 이내로 좁혔습니다.

 

1.서론

그림 1: 샘플 품질 대 효과적인 샘플링 계산(모델 매개변수의 수 × 샘플링 시 함수 평가 횟수). 우리는 ImageNet 512×512에서 다양한 모델의 샘플 품질을 FID(↓)로 측정하여 비교했습니다. 우리의 2단계 sCM은 효과적인 샘플링 계산의 10% 미만으로 사용하면서도 기존 최고의 생성 모델에 필적하는 샘플 품질을 달성했습니다.

 

확산 모델(Sohl-Dickstein et al., 2015; Song & Ermon, 2019; Ho et al., 2020; Song et al., 2021b)은 이미지(Rombach et al., 2022; Ramesh et al., 2022; Ho et al., 2022), 3D(Poole et al., 2022; Wang et al., 2024; Liu et al., 2023b), 오디오(Liu et al., 2023a; Evans et al., 2024), 비디오 생성(Blattmann et al., 2023; Brooks et al., 2024)에서 놀라운 결과를 달성하며 생성형 AI를 혁신해 왔습니다. 그러나 이 모델들의 큰 단점은 느린 샘플링 속도로, 단일 샘플을 생성하기 위해 수십에서 수백 단계가 필요하다는 점입니다. 이를 해결하기 위해 다양한 확산 증류 기법들이 제안되었는데, 여기에는 직접 증류(Luhman & Luhman, 2021; Zheng et al., 2023b), 적대적 증류(Wang et al., 2022; Sauer et al., 2023), 점진적 증류(Salimans & Ho, 2022), 그리고 변분 점수 증류(VSD)(Wang et al., 2024; Yin et al., 2024b; a; Luo et al., 2024; Xie et al., 2024b; Salimans et al., 2024) 등이 포함됩니다. 하지만 이 방법들은 각각 다음과 같은 문제들을 가지고 있습니다: 직접 증류는 다수의 확산 모델 샘플이 필요하기 때문에 계산 비용이 많이 들고, 적대적 증류는 GAN 훈련의 복잡성을 야기하며, 점진적 증류는 여러 훈련 단계가 필요하고 1~2단계 생성에는 비효율적이며, VSD는 지나치게 부드러운 샘플을 생성해 다양성이 부족하고 높은 가이드 수준에서 어려움을 겪습니다.

 

일관성 모델(CMs)(Song et al., 2023; Song & Dhariwal, 2023)은 이러한 문제를 해결하는 데 큰 이점을 제공합니다. CMs는 확산 모델 샘플의 감독 없이 훈련될 수 있어 합성 데이터셋을 생성하는 계산 비용을 피할 수 있으며, 적대적 훈련을 우회하여 그 복잡성을 피할 수 있습니다. 또한 CMs는 사전 훈련된 확산 모델에 의존하지 않고 일관성 훈련(CT)을 통해 처음부터 훈련될 수 있습니다. 이전 연구(Song & Dhariwal, 2023; Geng et al., 2024; Luo et al., 2023; Xie et al., 2024a)에서는 특히 1~2단계의 소수 단계 생성에서 CMs의 효과를 보여주었습니다. 하지만 이러한 결과들은 모두 이산 시간 CM에 기반하고 있어, 이산화 오류가 발생하고 시간 단계 그리드를 신중하게 조정해야 하는 문제로 인해 샘플 품질이 최적화되지 않을 수 있습니다. 반면, 연속 시간 CMs는 이러한 문제를 피할 수 있지만, 훈련 불안정성으로 어려움을 겪어왔습니다(Song et al., 2023; Song & Dhariwal, 2023; Geng et al., 2024).

 

그림 2: ImageNet 512×512에서 연속 시간 일관성 모델로 훈련된 2단계 샘플들.

 

본 연구에서는 연속 시간 CM의 훈련을 단순화하고 안정화하며 확장하기 위한 기법들을 소개합니다. 우리의 첫 번째 기여는 EDM(Karras et al., 2022; 2024)과 Flow Matching(Peluchetti, 2022; Lipman et al., 2022; Liu et al., 2022; Albergo et al., 2023; Heitz et al., 2023)을 통합하는 새로운 공식인 TrigFlow를 제안하여, 확산 모델, 관련 확률 흐름 ODE 및 CM의 공식을 크게 단순화한 것입니다. 이를 바탕으로 CM 훈련의 불안정성의 근본 원인을 분석하고, 이를 완화하기 위한 완전한 레시피를 제안합니다. 우리의 접근법에는 네트워크 아키텍처 내에서의 개선된 시간 조건화 및 적응형 그룹 정규화가 포함됩니다. 추가로, 연속 시간 CM을 위한 훈련 목표를 재공식화하고, 주요 용어의 적응형 가중치 부여 및 정규화, 그리고 점진적 소멸을 포함하여 안정적이고 확장 가능한 훈련을 가능하게 했습니다.

 

이러한 개선을 통해 우리는 일관성 훈련과 증류 모두에서 일관성 모델의 성능을 향상시켜, 이전의 이산 시간 공식과 비교하여 동일하거나 더 나은 결과를 달성했습니다. 우리는 sCM이라 부르는 모델들을 CIFAR-10, ImageNet 64×64, ImageNet 512×512에서 훈련하였으며, 15억 개의 매개변수를 가지는 전례 없는 규모에 도달했습니다(그림 2의 샘플 참조). sCM은 계산량이 증가함에 따라 예측 가능한 방식으로 더 나은 샘플 품질을 달성하면서 효과적으로 확장됩니다. 또한, 훨씬 더 많은 샘플링 계산이 필요한 최신 확산 모델과 비교했을 때, sCM은 두 단계의 생성으로 FID 격차를 10% 이내로 좁혔습니다. 추가적으로, 이산 시간 모델에 비해 연속 시간 CMs의 장점을 엄밀하게 정당화하고, 샘플 품질이 연속 시간 한계에 가까워질수록 인접한 시간 단계 간 간격이 좁아지며 개선된다는 것을 입증했습니다. 마지막으로, sCM과 VSD의 차이를 조사한 결과, sCM은 더 다양한 샘플을 생성하며 가이드와의 호환성이 더 좋은 반면, VSD는 높은 가이드 수준에서 어려움을 겪는 경향이 있음을 발견했습니다.

 

2.기초
2.1 확산 모델

 

우리는 확산 모델의 두 가지 최근 공식화를 고려합니다.

 

EDM (Karras et al., 2022; 2024)

Flow Matching

 

2.2 일관성 모델

그림 3: 이산 시간 CM(위 & 중간) vs. 연속 시간 CM(아래).
이산 시간 CM은 수치 ODE 해석기의 이산화 오류로 인해 훈련 중 불완전한 예측을 야기합니다. 반면 연속 시간 CM은 무한소 단계로 접선 방향을 따라 ODE 궤적에 머무릅니다.

 

 

이산 시간 CM

훈련 목표는 유한한 거리를 가진 두 인접한 시간 단계에서 정의됩니다:

 

연속 시간 CM

 

일관성 증류 및 일관성 훈련

 

3. 연속 시간 일관성 모델의 단순화

 

확산 과정

 

확산 모델 및 PF-ODE

 

확산 목표

 

일관성 모델

 

 

4. 연속 시간 일관성 모델의 안정화

연속 시간 CM을 훈련하는 것은 매우 불안정했습니다(Song et al., 2023; Geng et al., 2024). 그 결과, 이전 연구에서는 이산 시간 CM에 비해 성능이 현저히 떨어졌습니다. 이를 해결하기 위해, 우리는 TrigFlow 프레임워크를 기반으로 연속 시간 CM을 안정화하기 위한 여러 이론적으로 근거 있는 개선을 제안합니다. 특히 매개변수화, 네트워크 아키텍처, 훈련 목표에 중점을 두었습니다.

4.1 매개변수화와 네트워크 아키텍처

 

 

다음으로, 식 (7)의 각 구성 요소를 안정화하기 위한 개선사항을 설명합니다.

 

 

위치 기반 시간 임베딩

 

적응형 이중 정규화

 

그림 4에서 우리는 CIFAR-10에서 훈련된 CM의 시간 미분이 안정화된 모습을 시각화했습니다. 실험적으로, 이러한 개선이 CM의 훈련 역학을 안정화하는 데 도움이 되며, 확산 모델 훈련에 악영향을 미치지 않는다는 것을 확인했습니다(부록 G 참조).

 

 

 

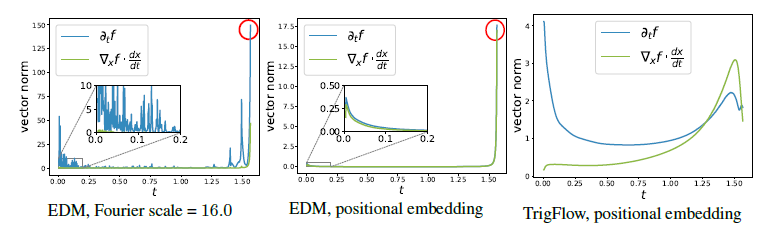
4.2 훈련 목표

 

접선 정규화

 

적응형 가중치 부여

확산 미세 조정 및 접선 워밍업

 

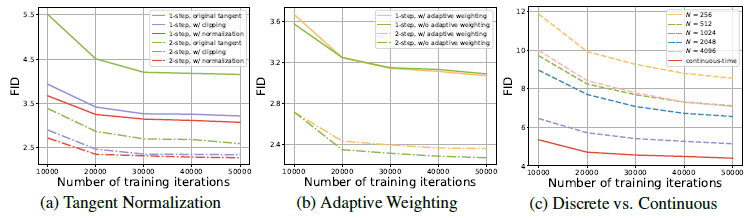
모든 기술이 적용된 상태에서, 이산 시간과 연속 시간 CM 훈련의 안정성은 크게 향상됩니다. 우리는 부록 E에서 이산 시간 CM에 대한 상세한 알고리즘을 제공하며, 같은 설정으로 연속 시간 및 이산 시간 CM을 훈련합니다. **그림 5(c)**에서 보여지듯이, 이산 시간 CM에서 이산화 단계 수 N을 증가시키면 이산화 오류를 줄여 샘플 품질이 향상되지만, N>1024 이후로는 수치적 정밀도 문제로 인해 성능이 저하됩니다. 반면, 연속 시간 CM은 모든 N에서 이산 시간 CM보다 훨씬 뛰어난 성능을 보여주며, 이는 연속 시간 CM을 이산 시간 CM보다 선택해야 할 강력한 근거를 제공합니다. 우리는 우리 모델을 sCM(단순함, 안정성, 확장 가능성을 의미)이라고 부르며, 부록 A에서 sCM 훈련에 대한 상세한 의사 코드를 제공합니다.

 

그림 6 설명: sCD는 교사 확산 모델과 비례적으로 확장됩니다. (a) FID와 (b) FID 비율을 같은 모델 크기의 교사 확산 모델에 대해 ImageNet 64×64와 512×512에서 비교한 결과입니다. sCD는 sCT보다 더 잘 확장되며, 모든 모델 크기에서 FID 비율에 일정한 오프셋이 존재하여 sCD가 교사 확산 모델과 동일한 확장 특성을 가지고 있음을 나타냅니다. 또한, 샘플링 단계가 증가함에 따라 오프셋이 줄어듭니다.

 

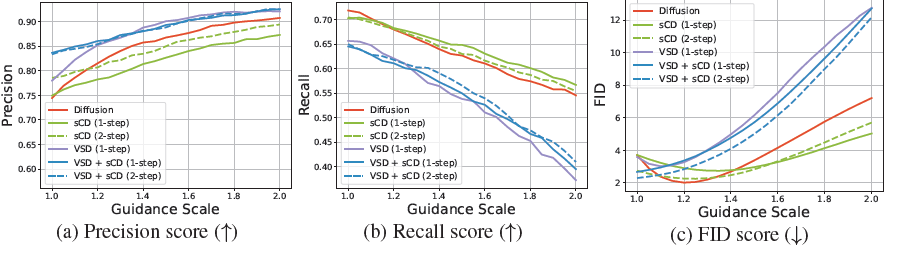
그림 7 설명: sCD는 VSD에 비해 더 높은 다양성을 가지고 있습니다. EDM2(Karras et al., 2024) 확산 모델, VSD(Wang et al., 2024; Yin et al., 2024b), sCD, 그리고 VSD와 sCD의 조합을 다양한 가이드 스케일에 대해 샘플 품질을 비교한 결과입니다. 모든 모델은 EDM2-M 크기이며 ImageNet 512×512에서 훈련되었습니다.

 

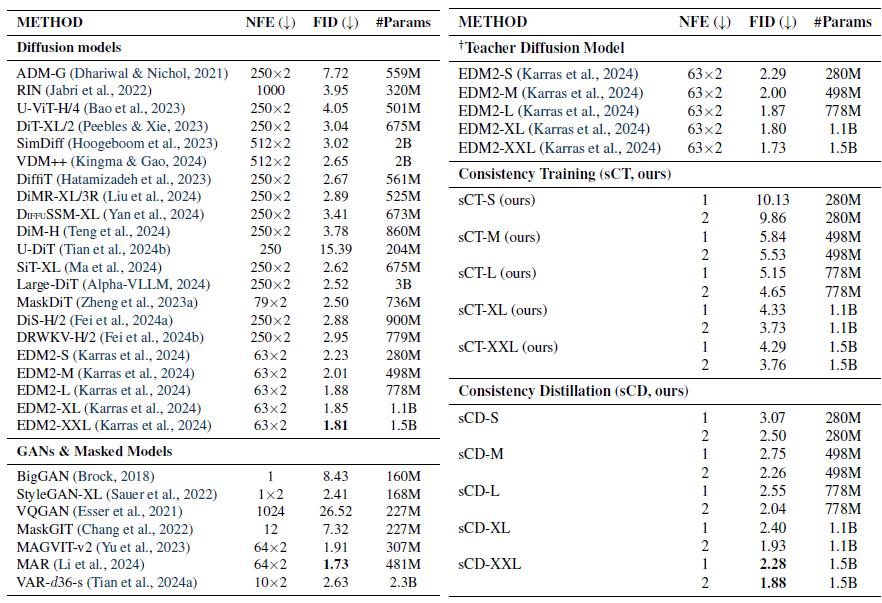
표 1: 무조건적 CIFAR-10 및 클래스 조건부 ImageNet 64×64에서의 샘플 품질.

 

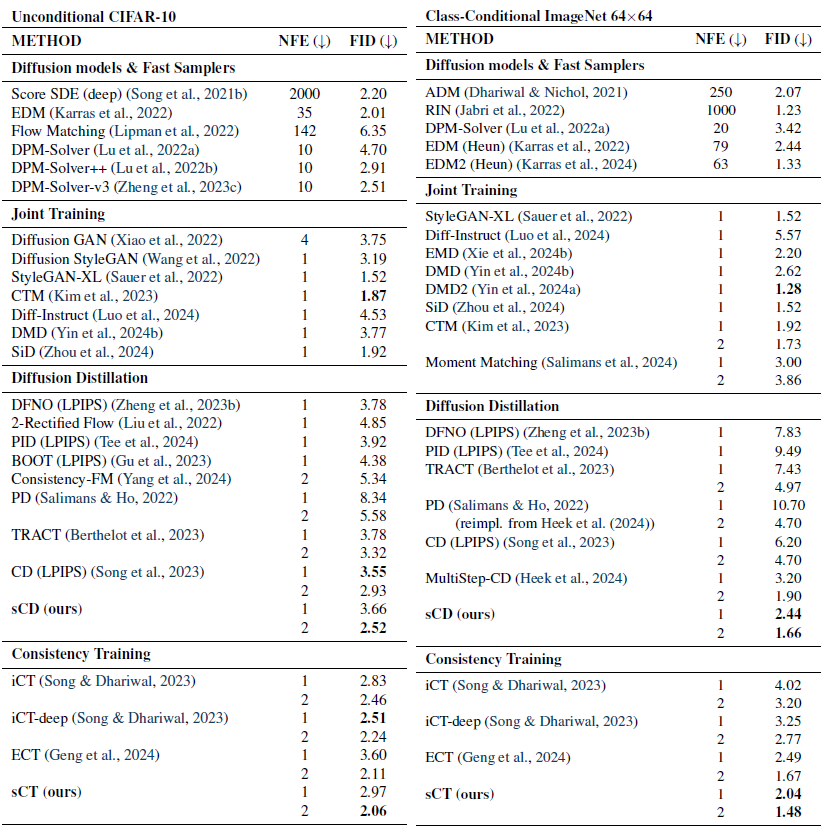
표 2: 클래스 조건부 ImageNet 512×512에서의 샘플 품질. †우리의 재구현된 교사 확산 모델은 EDM2(Karras et al., 2024)를 기반으로 하지만, 섹션 4.1에서의 수정 사항을 포함합니다.

 

5. 연속 시간 일관성 모델의 확장

아래에서는 이전 섹션에서 제안된 모든 개선 사항을 테스트하여 다양한 도전적인 데이터셋에서 대규모 sCM을 훈련해 봅니다.

5.1 대규모 모델에서의 접선 계산

JVP 재배열

Flash Attention의 JVP
Flash Attention(Dao et al., 2022; Dao, 2023)은 대규모 모델 훈련에서 주의 계산에 널리 사용되며, GPU 메모리를 절약하고 훈련 속도를 높입니다. 하지만 Flash Attention은 야코비안-벡터 곱(JVP)을 계산하지 않습니다. 이를 보완하기 위해, 우리는 Flash Attention 스타일로 소프트맥스 자기 주의와 그 JVP를 단일 전방 패스로 효율적으로 계산하는 유사한 알고리즘을 제안합니다(부록 F에 자세히 설명). 이 방법은 주의 층에서 JVP 계산을 위한 GPU 메모리 사용량을 크게 줄입니다.

 

5.2 실험

 

sCM의 훈련 연산량
모든 데이터셋에 대해 교사 확산 모델과 동일한 배치 크기를 사용했습니다. sCD의 훈련 반복당 효과적인 연산량은 교사 모델의 약 두 배에 해당합니다. 우리는 sCD의 2단계 샘플 품질이 빠르게 수렴하며, 교사 확산 모델의 20% 미만의 훈련 연산량으로 교사 모델과 비교 가능한 결과를 달성한다는 것을 관찰했습니다. 실제로 sCD를 사용한 경우, 단 2만 번의 미세 조정 반복 후에 고품질 샘플을 얻을 수 있었습니다.

 

벤치마크
표 1과 2에서 우리는 이전 방법들과의 비교를 위해 FID와 함수 평가 횟수(NFE)를 벤치마크하였습니다. 첫째로, sCM은 다른 네트워크와의 공동 훈련에 의존하지 않는 이전의 모든 몇 단계 생성 방법을 능가하며, 기존의 적대적 훈련을 통해 달성된 최고의 결과와 동등하거나 이를 초과합니다. 특히, ImageNet 512×512에서 sCD-XXL의 1단계 FID는 StyleGAN-XL(Sauer et al., 2022)와 VAR(Tian et al., 2024a)의 성능을 능가했습니다. 또한, sCD-XXL의 2단계 FID는 모든 생성 모델을 뛰어넘으며, 63개의 연속적인 단계가 필요한 기존의 최상위 확산 모델과도 비교 가능한 성능을 보입니다. 둘째로, 2단계 sCM 모델은 교사 확산 모델과의 FID 격차를 10% 이내로 좁혀 CIFAR-10에서는 2.06(FID 2.01인 교사 모델 대비), ImageNet 64×64에서는 1.48(교사 모델의 FID는 1.33), ImageNet 512×512에서는 1.88(교사 모델의 FID는 1.73)을 기록했습니다. 또한 sCT는 작은 규모에서 더 효과적이지만 큰 규모에서는 분산이 증가하는 경향을 보이는 반면, sCD는 작은 규모와 큰 규모 모두에서 일관된 성능을 보였습니다.

 

스케일링 연구
개선된 훈련 기법을 기반으로 연속 시간 CM을 훈련 불안정 없이 성공적으로 확장했습니다. 우리는 ImageNet 64×64와 512×512에서 EDM2 설정(S, M, L, XL, XXL)을 사용하여 다양한 크기의 sCM을 훈련하고 최적의 가이드 스케일에서 FID를 평가하였습니다(그림 6 참조). 첫째, 모델 FLOP이 증가함에 따라 sCT와 sCD 모두 샘플 품질이 향상되었으며, 두 방법 모두 스케일링으로 이득을 보았음을 알 수 있습니다. 둘째, sCD와 비교했을 때, sCT는 작은 해상도에서 더 계산 효율적이지만 큰 해상도에서는 덜 효율적입니다. 셋째, sCD는 주어진 데이터셋에 대해 예측 가능한 방식으로 스케일링되며, 모델 크기 전반에 걸쳐 FID에서 일관된 상대적 차이를 유지합니다. 이는 sCD의 FID가 교사 확산 모델과 같은 비율로 감소하며, 따라서 sCD도 교사 확산 모델만큼 확장 가능하다는 것을 시사합니다. 교사 확산 모델의 FID가 스케일링에 따라 감소함에 따라, sCD와 교사 모델 간의 FID의 절대적 차이도 줄어듭니다. 마지막으로, 더 많은 샘플링 단계에서 FID의 상대적 차이가 감소하며, 2단계 sCD의 샘플 품질은 교사 확산 모델과 동등해집니다.

 

VSD와의 비교
변분 점수 증류(VSD)(Wang et al., 2024; Yin et al., 2024b) 및 그 다단계 일반화(Xie et al., 2024b; Salimans et al., 2024)는 고해상도 이미지에서 확장 가능성을 입증한 또 다른 확산 증류 기법을 나타냅니다(Yin et al., 2024a). 우리는 EDM2-M 설정을 사용하여 교사 확산 모델을 미세 조정하기 위해 시간 T에서 0까지의 1단계 VSD를 적용하고, 공정한 비교를 위해 가중 함수와 제안 분포를 모두 조정했습니다. 그림 7에 나타난 바와 같이, 우리는 가이드 스케일을 변경하여 sCD, VSD, sCD와 VSD의 조합(두 손실을 단순히 합산한 것), 그리고 교사 확산 모델을 비교했습니다. 우리는 VSD가 확산 모델에서 큰 가이드 스케일을 적용했을 때와 유사한 아티팩트를 가지고 있음을 관찰했습니다: 이는 정확도(precision) 점수가 높아지는 것으로 볼 수 있듯이 충실도(fidelity)를 증가시키는 반면 다양성은 감소하여(recall 점수가 낮아짐) 심각한 모드 붕괴가 발생합니다. 반면, 2단계 sCD의 정확도와 재현율 점수는 교사 확산 모델과 비교할 만하며, VSD보다 더 나은 FID 점수를 달성합니다.

6. 결론

우리의 개선된 공식, 아키텍처, 훈련 목표는 연속 시간 일관성 모델의 훈련을 단순화하고 안정화하여 ImageNet 512×512에서 15억 개의 매개변수로의 원활한 확장을 가능하게 했습니다. 우리는 TrigFlow 공식, 접선 정규화, 적응형 가중치의 영향을 실험적으로 확인하여 그 효과를 입증했습니다. 이러한 개선을 결합한 결과, 우리 방법은 데이터셋과 모델 크기 전반에 걸쳐 예측 가능한 확장성을 보여주었고, 대규모에서 다른 몇 단계 샘플링 접근법들을 능가했습니다. 특히, 2단계 생성으로 교사 모델과의 FID 격차를 10% 이내로 줄였으며, 이는 훨씬 더 많은 샘플링 단계를 요구하는 최첨단 확산 모델들과 비교할 만한 성능입니다.

감사의 말

우리는 기술적 논의를 도와준 Allan Jabri, Aaron Lou, Alex Nichol, Huiwen Chang, Heewoo Jun, Ishaan Gulrajani에게 감사드리며, 플롯 및 다이어그램에 도움을 준 Mingyu Ye에게도 감사를 표합니다. 또한 이 연구 프로젝트에 대해 Mark Chen과 Prafulla Dhariwal의 지원에도 감사를 드립니다.