GRIN: GRadient-INformed MoE

https://arxiv.org/abs/2409.12136

GRIN: GRadient-INformed MoE

 

초록
Mixture-of-Experts (MoE) 모델은 전문가 라우팅을 통해 희소한 계산을 수행함으로써, 밀집 모델보다 더 효과적으로 확장됩니다. 이는 특정 전문가 모듈의 일부분만 선택적으로 활성화하기 때문입니다. 그러나 희소한 계산은 기존의 훈련 방식에 도전이 됩니다. 전문가 라우팅의 이산적 특성 때문에 표준 역전파와 경사 기반 최적화를 직접 사용할 수 없으며, 이들은 딥러닝의 핵심 기법입니다. MoE의 확장성을 최대한 활용하기 위해, 우리는 전문가 라우팅을 위한 희소 경사 추정 방법을 도입한 GRIN(GRadient-INformed MoE training)을 제안하며, 토큰 드롭핑을 피하기 위해 모델 병렬화를 구성합니다. GRIN을 자기회귀 언어 모델링에 적용하여, top-2 방식의 16 × 3.8B MoE 모델을 개발했습니다. 이 모델은 6.6B 개의 활성화된 파라미터만으로 7B 밀집 모델을 능가하며, 동일한 데이터로 훈련된 14B 밀집 모델과 동등한 성능을 보입니다. 다양한 과제를 통한 광범위한 평가 결과, GRIN은 MoE의 효과를 크게 향상시키며 MMLU에서 79.4, HellaSwag에서 83.7, HumanEval에서 74.4, MATH에서 58.9의 성능을 달성했습니다.

 

1. 서론
대규모 사전 훈련의 성공은 모델 확장성의 중요성을 강조합니다(OpenAI, 2023; Touvron et al., 2023). Mixture-of-Experts (MoE) 모델은 특정 입력에 따라 일부 모듈만 선택적으로 활성화하는 전문가 라우팅 과정을 통해 모델의 확장성을 크게 향상시키는 유망한 접근법으로 부상하고 있습니다(Lepikhin et al., 2021; Fedus et al., 2022; Zoph et al., 2022).

 

그러나 MoE의 희소 활성화 메커니즘은 모델 훈련에 몇 가지 어려움을 제공합니다. 예를 들어, 이산적 라우팅 함수는 비미분 가능 출력을 생성하는 반면, 딥러닝의 핵심인 역전파는 미분 가능 함수에서만 사용할 수 있습니다(Rosenblatt, 1957; Bengio et al., 2013). 결과적으로 역전파를 전문가 라우팅의 경사 계산에 직접 적용할 수 없습니다.

 

MoE의 확장 잠재력을 최대한 활용하기 위해, 우리는 이 연구에서 전문가 라우팅을 위한 경사 추정 방법을 연구하고 토큰 드롭핑을 방지하기 위해 모델 병렬화를 구성했습니다. Liu et al. (2023a, b)을 확장하여 우리는 전문가 라우팅에 대한 경사를 추정하기 위해 SparseMixer-v2를 제안하며, 이는 게이팅 경사를 라우팅 경사의 대리로 사용하는 기존 방식과 다릅니다. 또한, 우리는 용량 인자를 사용할 필요가 없고 훈련 중 토큰을 드롭하지 않는 파이프라인 병렬화와 텐서 병렬화를 사용하는 확장 가능한 MoE 훈련 방식을 제안합니다.

 

Figure 1: MMLU 정확도와 활성화된 파라미터.

 

Table 1: GRIN MoE의 세부 사항.

 

우리는 GRadient-INformed MoE(GRIN MoE)를 자기회귀 언어 모델링에 적용하고, 16×3.8B MoE 모델을 개발했습니다. 이 모델은 GRIN MoE로 지칭되며, MoE 레이어를 피드포워드 네트워크로 포함하고 각 레이어에서 16명의 전문가 중 2명을 선택하는 top-2 라우팅을 수행합니다. 구체적으로, 각 전문가는 GLU 네트워크로 구현되며, 라우팅 모듈은 각 레이어의 각 토큰에 대해 16명의 전문가 중 2명을 선택적으로 활성화합니다. 그 결과, 16 × 3.8B 모델은 총 42B의 파라미터를 가지며, 추론 시 6.6B의 파라미터가 활성화됩니다.

 

다양한 과제를 대상으로 한 평가에서 GRIN MoE는 특히 코딩과 수학 과제에서 매우 우수한 성능을 보였습니다. 예를 들어, MMLU에서는 79.4, HumanEval에서는 74.4, MBPP에서는 80.3, MATH에서는 58.9의 점수를 기록했습니다. GRIN MoE는 동일한 데이터로 훈련된 밀집 모델과 비교하여도 우수한 성능을 보였습니다. 예를 들어, GRIN MoE는 Table 2에서 평균 79.58점을 기록하며, 7B 밀집 모델(평균 75.74점)을 능가하고 14B 밀집 모델(평균 78.46점)과 동등한 성능을 보였습니다.

 

또한, 우리는 GRIN MoE가 잘 작동하는 이유를 밝히기 위해 심층 분석을 수행했습니다. 우리는 GRIN MoE가 복잡한 질문에 올바르게 답하고 빠르게 힌트를 습득할 수 있으며, 과제와 도메인에 따라 전문가 할당 패턴이 다르다는 것을 보여주었습니다. 이는 전문가들이 특정 전문성을 개발했으며, 라우터가 이 전문가들을 효과적으로 조합할 수 있음을 나타냅니다.

 

2. 모델 아키텍처
기존 최첨단 MoE 모델과 유사하게, GRIN MoE는 트랜스포머 아키텍처(Vaswani et al., 2017)를 기반으로 트랜스포머 블록을 쌓아 올린 구조를 가지고 있습니다.

 

트랜스포머
트랜스포머 네트워크는 트랜스포머 블록들을 쌓아 구성되며, 각 블록은 어텐션 레이어와 피드포워드 레이어로 이루어져 있습니다. 모든 서브 레이어에는 잔차 연결과 레이어 정규화가 Pre-LN 방식으로 적용됩니다.

 

어텐션
Mistral(Jiang et al., 2023b)을 따라, 우리는 어텐션 레이어를 그룹 쿼리 어텐션(Ainslie et al., 2023)과 슬라이딩 윈도우 어텐션(Child et al., 2019)을 통해 구현했습니다. 두 기술 모두 계산 효율성이 뛰어나며, GRIN MoE가 윈도우 크기를 넘어선 정보를 처리할 수 있도록 합니다. 위치 인코딩에는 RoPE를 사용하여 사전 훈련 이후 긴 컨텍스트를 인코딩할 수 있도록 했습니다(Su et al., 2024). 우리의 구현은 대부분 FlashAttention 2 (Dao, 2023)를 기반으로 하고 있습니다.

 

Mixture of Experts
기존 트랜스포머 모델과 달리, 우리는 피드포워드 레이어를 Mixture-of-Experts 레이어로 구성하고 라우터 네트워크를 사용하여 각 입력에 대해 선택적으로 네트워크를 희소하게 활성화합니다.

 

MoE의 개념은 처음 Jacobs et al. (1991)과 Jordan & Jacobs (1994)에서 논의되었으며, 개별 네트워크를 통합하여 각 네트워크가 훈련 사례의 특정 부분을 처리하도록 합니다. 최근에는 대규모 언어 모델의 확장을 위해 MoE를 활용하려는 시도가 많이 이루어졌습니다(Shazeer et al., 2017; Lepikhin et al., 2021; Lewis et al., 2021; Kim et al., 2021; Lepikhin et al., 2021; Fedus et al., 2022; Zoph et al., 2022).

 

각 MoE 레이어는 라우터 네트워크에 의해 매 입력 토큰마다 서로 다른 피드포워드 네트워크 중 하나를 선택합니다. 특히, n개의 전문가 파라미터 { 𝒘 0 , ⋯ , 𝒘 n − 1 } 가 주어졌을 때, 추론을 위한 하나의 MoE 모듈의 출력은 다음과 같습니다.

 

 

여기서 z=Router(x,r), r은 라우터의 파라미터이며, Gating(⋅)은 게이팅 함수(일반적으로 소프트맥스)이고, Expert(⋅)는 피드포워드 네트워크(FNN)입니다. 본 연구에서는 라우터를 선형 네트워크로 정의하여, Router(x,r)=x⋅r^T로 설정합니다. TopK(z)는 TopK 함수로, TopK(z)_i:=1은 z_i의 TopK 좌표에 속할 경우, 그렇지 않을 경우에는 TopK(z)_i:=0으로 정의됩니다.

 

모델 훈련 중에 다양한 MoE 알고리즘은 서로 다른 출력을 생성할 수 있으며, 이에 대해서는 3장에서 자세히 논의할 것입니다.

 

Table 2: 주요 벤치마크에서의 모델 성능.

 

3. GRIN MoE
이 섹션에서는 GRIN MoE에 사용된 두 가지 핵심 기술을 자세히 설명합니다:

• 우리는 전문가 라우팅과 관련된 경사를 추정하기 위해 SparseMixer-v2를 제안하며, 기존의 MoE 훈련에서는 전문가 게이팅을 경사 추정의 대리자로 취급합니다.
• 우리는 MoE 훈련을 전문가 병렬화나 토큰 드롭핑 없이 확장하며, 기존 MoE 훈련에서는 전문가 병렬화를 사용하고 토큰 드롭핑을 적용합니다.

3.1 전문가 라우팅을 위한 경사 추정

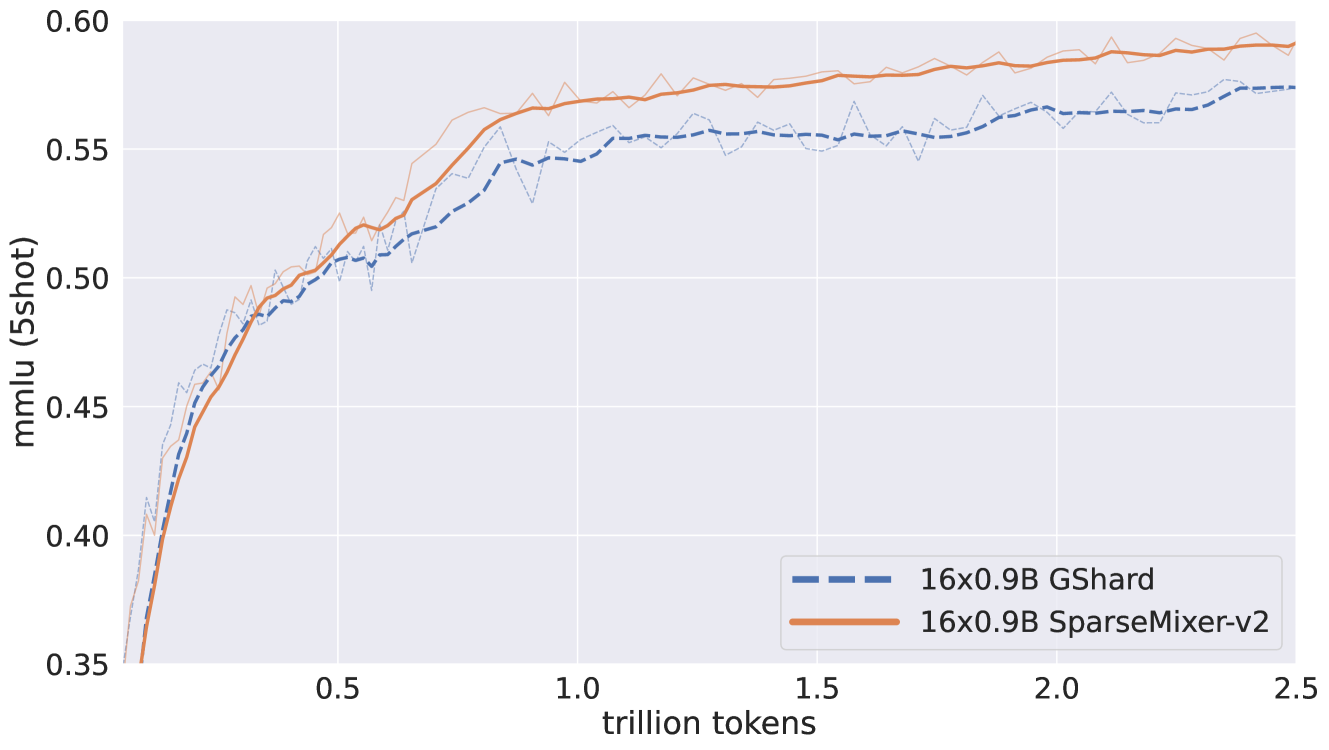
그림 2: SparseMixer-v2와 GShard의 16 × 0.9B MoE에서의 통제된 비교.

전문가 라우팅은 이산적인 전문가 할당을 생성하여 네트워크를 희소하게 활성화함으로써 큰 확장 잠재력을 제공합니다. 동시에, 이러한 라우팅 과정은 미분 가능하지 않기 때문에 기본적인 역전파를 직접 적용하여 신뢰할 수 있는 경사 추정을 얻는 것이 불가능합니다.

 

기존 MoE 훈련
기존의 MoE 훈련에서는 라우터 출력을 사용하여 게이팅 결과를 계산하고, 게이팅 경사를 라우터 경사의 대리자로 취급합니다. 특히, 식 (1)과 같이 MoE 모듈의 출력은 다음과 같습니다:

 

SparseMixer-v2
최근의 스트레이트-스루 경사 추정기(Bengio et al., 2013; Liu et al., 2023a)의 발전에 영감을 받아, 우리는 SparseMixer(Liu et al., 2023b)의 확장판인 SparseMixer-v2를 제안하여 확장 가능하고 신뢰할 수 있는 경사 추정을 제공합니다.

 

아래에서 SparseMixer-v2 방법을 간단히 소개하고, 자세한 설명은 부록 A에 남겨두겠습니다. 우리는 먼저 TopK(⋅)함수를 모델 훈련 시 이산 변수의 무작위 샘플링으로 대체합니다. 그런 다음, Liu et al. (2023a, b)를 따라, Heun의 3차 방법을 적용하여 전문가 라우팅 경사를 근사하고, 수정된 역전파를 구성하여 전문가 라우팅에 대해 수학적으로 타당한 경사 추정을 제공합니다.

 

SparseMixer-v2의 효과성
Liu et al. (2023b)에서는 SparseMixer의 효과성이 신경 기계 번역 작업과 ELECTRA 언어 모델 훈련에서 입증되었습니다. 그러나 이는 대규모 자기회귀 언어 모델 훈련에는 적용된 적이 없었습니다. GRIN MoE의 개발에서 우리는 SparseMixer-v2에 대해 통제된 실험을 수행하였으며, 긍정적인 결과를 얻었습니다. 이러한 결과는 이 알고리즘을 GRIN MoE 훈련에 적용할 수 있는 동기를 제공했습니다.

 

특히, 우리는 16 × 0.9B 크기의 두 MoE를 2.5T 토큰으로 훈련했습니다. 하나는 GRIN MoE에 사용된 것과 동일한 레시피를 따랐으며, 다른 하나는 SparseMixer-v2를 기존의 GShard 방법으로 대체했습니다. 그림 2에서 볼 수 있듯이, SparseMixer-v2의 성능 향상은 16 × 0.9B 규모의 자기회귀 언어 모델 훈련에도 일반화되었습니다. 비록 GShard가 처음 0.5T 토큰 동안 더 나은 성능을 보였지만, SparseMixer-v2는 훈련 후반부에서 더 강한 성능을 발휘했습니다. ELECTRA 사전 훈련의 소규모 실험에서도 비슷한 현상이 관찰되었으며, Switch가 초기에는 더 잘 수행되다가 SparseMixer가 후반에 따라잡는 경향을 보였습니다(Liu et al., 2023b). 우리는 이것이 모델 아키텍처의 차이 때문이라고 의심하며, 예를 들어 TopK(⋅) 함수를 이산 변수의 무작위 샘플링으로 대체하여 훈련에 더 많은 무작위성을 도입함으로써, 초기 훈련 속도가 느려질 수 있습니다. 또한, 이러한 추가적인 무작위성이 GShard와의 훈련 손실 비교를 어렵게 만든다는 점도 언급할 가치가 있습니다. 더 큰 규모에서의 반통제 실험 결과는 섹션 5에서 논의됩니다.

 

3.2 구현 및 확장성
기존 모델이 모든 입력에 대해 모든 파라미터를 활성화하는 것과 비교하여, MoE 모델은 구조적으로 희소한 계산 덕분에 동일한 FLOPs(초당 부동소수점 연산)에서 더 많은 파라미터를 가지며, 이는 계산 효율성에 큰 영향을 미칩니다. 기존 MoE 훈련에서는 다른 전문가 네트워크들을 장치 간에 분산시켜(즉, 전문가 병렬화) 훈련을 촉진하기 위해 토큰 드롭핑과 같은 전략을 사용합니다.

 

MoE가 제공하는 확장성을 추구하기 위한 첫 번째 단계로, 우리는 상대적으로 적은 수의 전문가(예: 16명의 전문가 중 top2 라우팅)를 사용하는 MoE 훈련에 집중합니다. 최근의 엔지니어링 발전을 활용하여 우리는 전문가 병렬화를 피하고 용량 인자나 토큰 드롭핑의 필요성을 제거했습니다. 그 결과, 동일한 활성 파라미터를 가진 밀집 모델과 비교했을 때, GRIN MoE 훈련에서 80% 이상의 상대적 훈련 효율성 향상을 달성할 수 있었습니다.

 

-----

이 문장은 GRIN MoE 모델의 훈련 과정이 기존 밀집(dense) 모델과 비교했을 때 상대적으로 더 효율적이었다는 의미입니다. 여기서 중요한 것은 "동일한 활성 파라미터"라는 부분입니다.

조금 더 자세히 설명하자면:

• 활성 파라미터(active parameters): 모델이 특정 입력에 대해 실제로 사용하는 파라미터의 수를 의미합니다. MoE 모델에서는 모든 파라미터를 활성화하는 대신, 특정 전문가(expert)만 선택적으로 활성화하여 사용하기 때문에 계산이 더 희소하게(sparse) 이루어집니다.
• 밀집 모델(dense model): 모든 입력에 대해 모든 파라미터가 항상 활성화되는 모델을 의미합니다. 이와 달리, MoE 모델은 특정 입력에 대해서 일부 전문가들만 선택적으로 활성화함으로써 희소한 계산을 합니다.

GRIN MoE 훈련은 희소하게 계산을 하지만, 이를 통해 밀집 모델과 비교했을 때 상대적인 훈련 효율성을 크게 향상시켰다는 뜻입니다. 구체적으로는, 밀집 모델이 동일한 수의 활성 파라미터를 가지고 훈련할 때 소모되는 계산량과 비교했을 때, GRIN MoE는 80% 더 효율적으로 훈련을 수행할 수 있었습니다. 즉, 더 적은 계산 자원으로 밀집 모델에 비해 유사하거나 더 나은 성능을 낼 수 있는 효율적인 모델이 된 것입니다.

이렇게 함으로써 더 많은 파라미터를 가지고도 효율적으로 훈련할 수 있다는 장점이 생기고, 이는 대규모 모델 훈련 시 계산 자원을 절약하거나 더 큰 모델을 사용해 성능을 높이는 데 유리하게 작용합니다.

-----

 

MoE 구현
전문가 병렬화 없이 MoE를 구현하기 위해 우리는 Megablocks(Gale et al., 2023) 패키지가 매우 유용하다는 것을 발견했습니다. 특히, grouped_GEMM 커널과 래퍼가 희소 버전보다 성능이 뛰어나 큰 성능 향상을 제공한다는 점을 발견했습니다. 또한, GRIN MoE의 훈련에서는 데이터 병렬화, 파이프라인 병렬화, 그리고 활성화 체크포인팅을 활용하여 16×3.8B 모델의 최대 처리량을 달성했습니다.

 

밀집 모델과 MoE 모델의 훈련 처리량 비교
MoE 훈련의 이점을 보여주기 위해, 우리는 전통적인 밀집 모델과의 훈련 처리량을 비교했습니다. 이러한 연구를 위한 하드웨어 세부 사항은 부록 B에 나와 있습니다. 여기서 중요한 점은, 밀집 모델의 처리량은 MoE 모델과 동일한 병렬화 설정에서 측정되었으며, 이 비교는 밀집하게 활성화된 네트워크(즉, 밀집 모델)와 희소하게 활성화된 네트워크(즉, MoE)의 GPU 커널 효율성을 연구하기 위한 것입니다.

 

표 3: 64개의 H100 GPU에서 밀집 모델과 MoE 모델의 훈련 처리량.

 

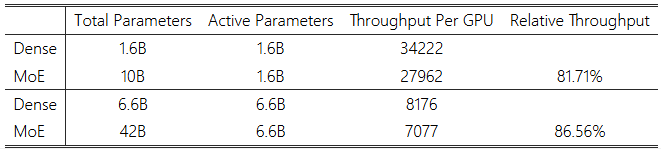
표 3에 요약된 바와 같이, 우리는 동일한 하드웨어를 사용하여 두 가지 다른 크기의 MoE 모델과 동일한 수의 파라미터를 가진 밀집 모델을 비교하여 훈련 처리량을 측정했습니다. MoE 모델은 밀집 모델보다 여섯 배 이상 많은 파라미터를 가지고 있음에도 불구하고, 이 실험에서는 80% 이상의 상대적 처리량을 달성하여 GRIN MoE 방법으로 모델의 계산적 확장 잠재력을 확인했습니다.

 

또한 우리의 관찰에 따르면, MoE 모델이 모델 크기를 확장할 때 밀집 모델보다 더 심각하거나 다른 형태의 처리량 감소를 경험하지 않는다는 점도 확인할 수 있었습니다. 실험에서 밀집 모델과 MoE 모델 모두 유사한 속도 저하 패턴을 보였습니다. 예를 들어, 6.6B 밀집 모델의 훈련 처리량은 1.6B 밀집 모델에 비해 약 4.19배 느렸으며, 이는 파라미터 수가 4배 적은 모델과 비교된 것입니다. 유사하게, 42B MoE 모델의 훈련 처리량은 10B MoE 모델에 비해 약 3.96배 느렸으며, 이는 파라미터 수가 4.2배 적은 모델과 비교된 것입니다.

 

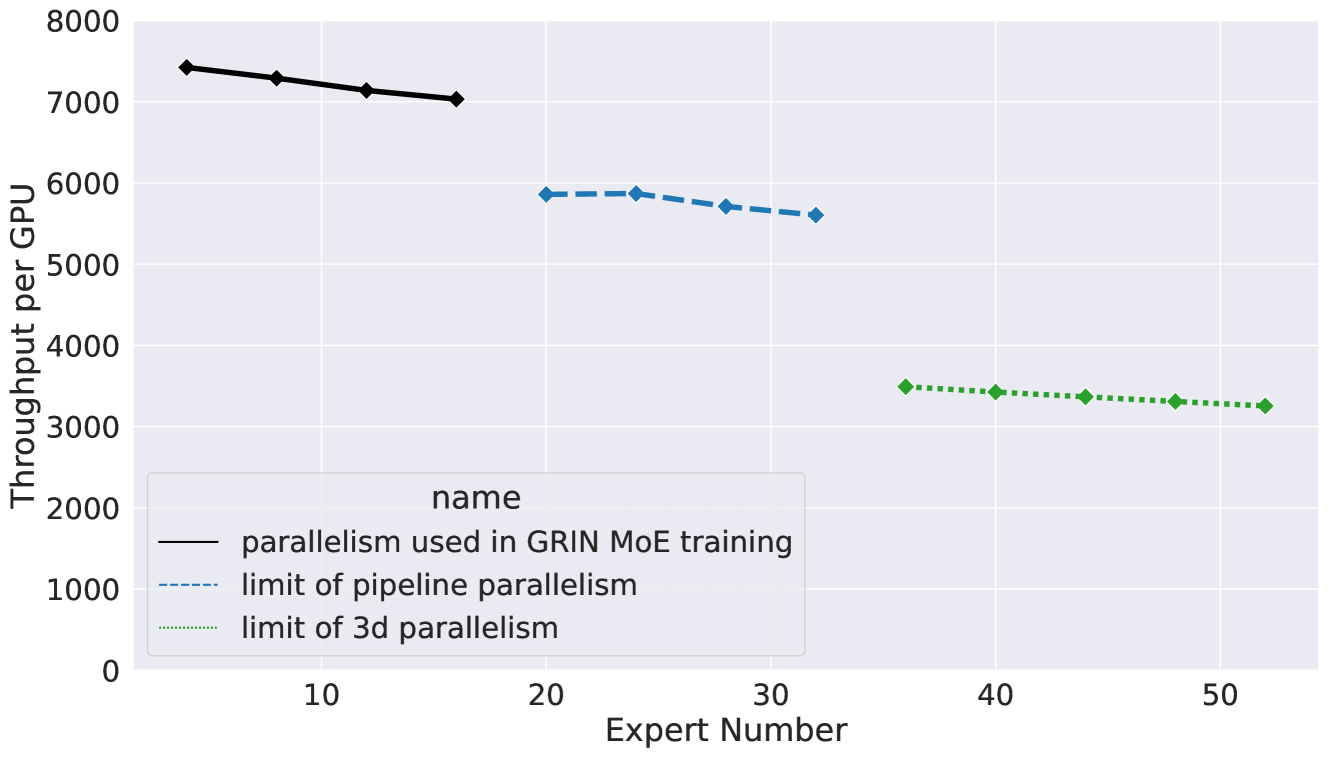
그림 3: 64개의 H100 GPU에서 다양한 병렬화 설정의 확장성. 보고된 전문가 수(N, x축)에 대한 처리량은 3.8B×N top2 MoE의 평균 훈련 처리량을 의미합니다.

 

확장 연구 및 텐서 병렬화
이 섹션에서는 전문가 병렬화 없이 더 많은 수의 전문가를 가진 MoE 모델을 훈련하는 것이 계산적으로 가능한지에 대해 논의합니다.

 

먼저, 파이프라인 병렬화만을 사용함으로써, GPU 간에 서로 다른 레이어를 추가로 분할하여 전문가 수를 최대 16에서 32로 확장할 수 있습니다. 그러나 이를 초과하는 전문가 수를 증가시키면 하나의 레이어에 너무 많은 파라미터가 생기게 되어, 단일 레이어를 여러 GPU에 걸쳐 분할하지 않는 한 지원하기 어려워집니다.

 

이 문제를 해결하기 위해, 기존의 MoE 훈련에서는 전문가 병렬화를 사용하여 모델을 추가로 분할하며, 이는 용량 인자와 토큰 드롭핑이라는 부작용을 가져옵니다. 우리의 연구에서는 전문가 병렬화 대신 텐서 병렬화(Narayanan et al., 2021)를 사용하는 것을 탐구했습니다. 전문가 병렬화와 유사하게, 텐서 병렬화도 순방향과 역방향 계산에서 각각 두 번의 all-reduce 통신 오버헤드를 가지며, 이 오버헤드는 역방향 계산 중에 통신과 계산을 중첩하여 완화할 수 있습니다.

 

그림 3과 같이, 파이프라인 병렬화와 텐서 병렬화(즉, 3D 병렬화)를 결합하여 지원 가능한 전문가 수를 52명(총 132B 파라미터)까지 확장했습니다. 여기서 중요한 점은, 우리의 처리량 연구 하드웨어 설정이 64개의 GPU만을 가지고 있으므로, 우리는 모델을 최대 64개의 단계로만 분할할 수 있다는 점입니다. 272개의 H100 GPU가 있다면, 이 병렬화의 한계는 200명 이상의 전문가로 더욱 확장될 수 있습니다.

 

이러한 결과는 전문가 병렬화 없이 MoE 훈련을 확장하는 것이 가능하다는 것을 보여주지만, 보다 복잡한 병렬화를 사용하면 일반적으로 계산 처리량이 감소하는 경향이 있다는 것도 관찰했습니다. 따라서 우리의 미래 작업의 중요한 방향 중 하나는 더 많은 전문가를 더욱 희소한 방식으로 사용하는 MoE 훈련을 수행하는 것입니다.

 

-----

이 문장은 앞으로의 연구 방향 중 하나가 "더 많은 전문가를, 더욱 희소하게 사용하는 방식으로 MoE 훈련을 수행하는 것"이라는 의미입니다. 여기서 "더 많은 전문가"와 "더욱 희소한 방식"이 중요한 키워드입니다. 각각을 좀 더 구체적으로 설명하자면 다음과 같습니다.

1. 더 많은 전문가: Mixture-of-Experts(MoE) 모델은 여러 전문가 네트워크 중 일부만 활성화하여 사용하는 구조를 가지고 있습니다. 이때 전문가의 수를 늘리게 되면 모델이 처리할 수 있는 지식의 다양성이나 복잡한 문제에 대한 대응 능력이 향상됩니다. 그러나 전문가의 수가 늘어날수록 관리해야 할 파라미터의 수도 늘어나기 때문에, 계산량이 증가하고 훈련의 어려움도 커지게 됩니다.
2. 더욱 희소한 방식: 희소하게 사용하는 것은 여러 전문가 중에서도 일부만 선택해서 활성화하는 방식을 의미합니다. MoE는 입력에 따라 특정 전문가들만 활성화하기 때문에 희소한 계산을 수행합니다. "더욱 희소한 방식"이란 더 적은 수의 전문가만 선택하여 활성화하는 것을 의미합니다. 이렇게 하면 계산 비용이 줄어들어 효율적인 훈련이 가능해집니다.

즉, 이 문장은 미래 작업의 목표가 더 많은 전문가 네트워크를 구축하지만, 이들 중 극히 일부만 선택해서 활성화하는 방식으로 MoE 모델을 훈련하겠다는 것을 의미합니다. 이를 통해 모델의 파라미터 수를 증가시키면서도 계산 자원은 효율적으로 사용하여, 성능을 높이는 동시에 훈련 비용을 줄이려는 방향을 제안하고 있는 것입니다.

이렇게 함으로써 MoE 모델의 확장성을 유지하면서도 계산 효율성을 극대화하는 방법을 모색하는 것이 목표입니다.

-----

 

3.3 전역 부하 균형 손실 적응
앞서 논의한 바와 같이, 우리의 훈련 프레임워크는 텐서 병렬화, 파이프라인 병렬화, 그리고 데이터 병렬화를 사용하여 MoE 훈련을 확장하도록 설계되었으며, 전문가 병렬화는 사용하지 않습니다. 따라서 토큰 드롭핑이나 용량 인자를 사용할 필요가 없으며, 활성화된 전문가의 분포가 균일 분포에서 벗어나도록 허용합니다.

 

따라서 우리는 부하 균형 손실을 로컬 부하 균형 대신 전역 전문가 부하 균형을 규제하도록 조정합니다. 특히, 일반적으로 사용되는 부하 균형 손실은 다음과 같이 정의됩니다:

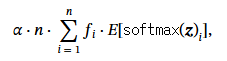
여기서 α는 하이퍼 파라미터이고, n은 전문가의 수이며, f_i​는 전문가 i에게 전달된 토큰의 비율을 의미합니다(Fedus et al., 2022). 전통적으로 f_i​는 각 GPU에서 로컬하게 계산되며, 따라서 부하 균형 손실은 로컬 전문가 부하 균형을 규제하고 토큰 드롭핑을 완화합니다. 우리의 연구에서는 부하 균형 보조 손실을 f_i​를 전역적으로(즉, 데이터 병렬 처리 그룹 내에서 모든 노드 간에 all-reduce) 계산하여, 전문가 부하가 전역적으로 균형을 이루도록 수정했습니다. 이 조정은 추가적인 통신 오버헤드를 발생시키지만, 텐서 병렬화와 유사하게 이러한 통신은 비동기적으로 계산과 병행하여 수행될 수 있어 추가적인 지연을 크게 줄일 수 있습니다.

 

4. 실험
4.1 훈련 설정
사전 훈련
GRIN MoE는 4T개의 토큰을 이용하여 인과 언어 모델(Causal Language Model)로 사전 훈련되었습니다. 동일한 훈련 데이터셋은 Phi-3 밀집 모델(Abdin et al., 2024)의 훈련에도 사용되었습니다.

 

후속 훈련
후속 훈련은 두 단계로 구성됩니다: 인과 언어 모델링 목표를 기반으로 한 지도 학습(Supervised Fine-Tuning, SFT), 그 뒤에 선호도 직접 최적화(Direct Preference Optimization, DPO; Rafailov et al., 2024)가 이어집니다. 모델은 SFT에서 240억 개의 토큰을 사용해 훈련되었으며, 수학, 코딩, 대화와 같은 다양한 범주의 고품질 데이터를 사용했습니다(Abdin et al., 2024). DPO 데이터셋에는 안전 및 정체성 선호도 데이터가 포함된 14억 개의 토큰이 포함되어 있으며, 이는 모델 출력을 마이크로소프트의 책임 있는 AI 원칙에 맞추기 위해 사용됩니다(Haider et al., 2024). 우리는 또한 일반화 성능을 향상시키기 위해 입력 임베딩에 무작위 노이즈를 추가하는 것(Jain et al., 2024)과 전문가 레이어에 드롭아웃을 적용하는 것(Fedus et al., 2022)과 같은 정규화 기법을 채택했습니다. 추가로, 긴 문맥 및 다국어 능력에 중점을 둔 또 다른 버전의 중간 훈련 및 후속 훈련이 수행되었으며, 이는 Phi-3.5-MoE로 공개되었습니다(Abdin et al., 2024).

 

4.2 GRIN MoE의 평가
표 2는 주요 벤치마크에서 GRIN MoE의 성능을 요약한 것입니다. 벤치마크와 기준 방법에 대한 자세한 내용은 부록 B에 설명되어 있습니다.

 

Phi-3와 GRIN MoE 모델이 동일한 데이터셋으로 훈련되었기 때문에, 우리의 MoE 훈련 방법의 효과는 쉽게 입증됩니다. GRIN MoE는 6.6B 개의 활성화된 파라미터로 7B 밀집 모델보다 상당히 더 나은 성능을 보였으며, 14B 밀집 모델과 비슷한 성능을 보여줍니다. 14B 밀집 모델과 비교했을 때, GRIN MoE는 수학, 코딩, MMLU 작업에서 더 우수한 성능을 보였습니다.

 

다국어 능력 및 긴 문맥 처리에 중점을 두고 개발된 Phi-3.5-MoE와 GRIN MoE를 비교해본 결과, 이 두 모델은 각기 다른 강점을 가지고 있음을 알 수 있었습니다. GRIN MoE는 수학 및 추론 작업에서 뛰어난 성능을 발휘하는 반면, Phi-3.5-MoE는 질문-응답(QA) 작업에서 우수한 성능을 보였습니다. 비록 이들 모델이 다른 강점을 가지고 있지만, 다양한 벤치마크에서 평균 점수는 유사하게 나타났습니다. 이는 두 모델 모두 16×3.8B MoE로 구성되었고 희소 역전파(sparse backpropagation)로 훈련되었기 때문에 예상된 결과입니다. 더 자세한 비교는 섹션 4.3에 나와 있습니다.

 

우리의 평가 결과에 따르면, GRIN MoE는 Mixtral 8×7B(활성화된 파라미터 12.9B), Mistral 7B, Gemma 7B, Llama3 8B와 같은 유사한 수의 활성화된 파라미터를 가진 많은 오픈소스 모델보다 뛰어난 성능을 보였습니다. 또한, 대부분의 작업에서 GRIN MoE는 Mixtral 8×22B보다 더 나은 성능을 보였습니다. 그럼에도 불구하고, GRIN MoE의 성능은 Llama3 70B와 GPT-4o에는 미치지 못했습니다. 이러한 차이는 후자의 두 모델이 훈련 시 상당히 더 많은 계산 및 데이터 자원을 사용했기 때문에 예상된 결과입니다.

 

4.3 수학 능력 사례 연구
GRIN MoE의 훈련 데이터인 Phi-3 데이터는 대량의 합성 데이터를 포함하고 있어 벤치마크에서 모델의 성능을 크게 향상시켰습니다. 그러나 이러한 데이터의 효과성에도 불구하고, GRIN MoE가 실제 작업에서 어떻게 성능을 발휘할지에 대한 의문이 남았습니다. 이에 따라, 우리는 최근 발표된 'GAOKAO' 시험(즉, 중국 대학 입학을 위한 연례 국가시험)의 수학 문제를 대상으로 사례 연구를 진행했습니다. 이 시험은 엄격한 보안 프로토콜로 잘 알려져 있어 AI 모델의 수학 문제 해결 능력을 평가하기 위한 "진정한 미사용 데이터" 테스트 베드로 이상적입니다. GRIN MoE의 훈련은 태평양 표준시로 6월 3일에 종료되었으며, 2024년 GAOKAO는 중국 표준시로 6월 7일에 시작되었습니다.

 

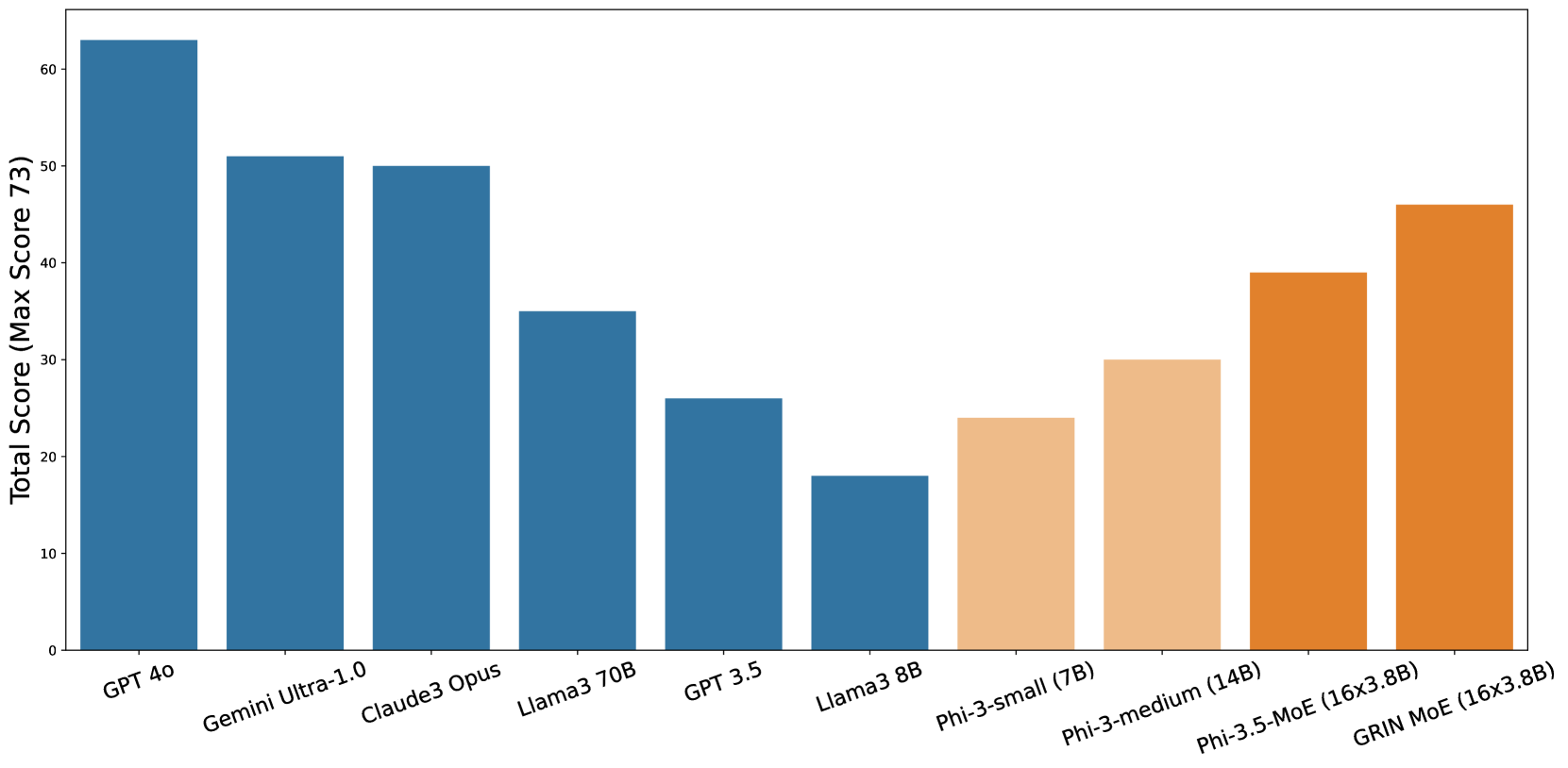
그림 4: 번역된 2024 GAOKAO 수학-1 시험 점수.

 

시험 점수
다양한 모델의 수학 문제 해결 능력을 평가하기 위해 번역된 문제를 입력으로 사용하고, 수동으로 응답을 채점하여 그림 4에 그 결과를 시각화했습니다(자세한 점수 결과와 GRIN MoE의 응답은 부록 C에서 확인할 수 있습니다). GRIN MoE는 이 문제에서 73점 만점에 46점을 기록하였으며, Llama3 70B보다 11점 더 높았습니다. 또한 Gemini Ultra-1.0과 Claude3 Opus보다 각각 6점과 5점 차이로 근접한 성적을 기록했습니다.

 

이러한 결과는 GRIN MoE의 뛰어난 수학적 추론 능력을 입증합니다. 이번 사례 연구에서 데이터 유출 가능성이 낮았기 때문에, 이 결과는 GRIN MoE의 능력이 단순한 암기보다는 생성적 디스틸레이션 접근(Hsieh et al., 2023; Mukherjee et al., 2023)에 기인할 가능성이 높음을 시사합니다.

 

-----

이 문장은 GRIN MoE가 수학 문제를 잘 푼 이유가 단순히 "훈련 데이터에서 해당 문제를 기억"한 것이 아니라, "생성적 디스틸레이션(generative distillation)"이라는 기법 덕분이라는 것을 시사한다는 의미입니다. 여기서 좀 더 구체적으로 설명하자면:

1. 수학적 추론 능력: GRIN MoE가 어려운 수학 문제들을 성공적으로 해결한 것은 모델이 수학적으로 논리적 추론을 잘 할 수 있다는 것을 의미합니다. 모델이 이런 능력을 보인다는 것은 단순히 많은 데이터를 기반으로 답을 암기하고 있는 것이 아니라, 새로운 문제를 보고 논리적으로 풀어내는 능력이 있다는 것을 뜻합니다.
2. 데이터 유출 가능성이 낮음: 사례 연구에서 사용된 GAOKAO 시험은 GRIN MoE의 훈련 데이터에 포함되지 않았으며, 실제로 이 시험 문제는 훈련 이후에 발생한 것이기 때문에 데이터 유출(모델이 훈련 중 해당 문제를 봤을 가능성)이 낮습니다. 즉, GRIN MoE가 이런 시험 문제들을 맞출 수 있었던 것은 훈련 데이터에 대한 단순한 암기 때문이 아닐 가능성이 높습니다.
3. 생성적 디스틸레이션(generative distillation): 생성적 디스틸레이션은 모델이 지식을 생성적으로 학습하고 이를 추론하는 방식으로 활용하는 기법입니다. 이는 단순히 데이터를 반복적으로 학습해서 답을 기억하는 것이 아니라, 학습한 지식을 바탕으로 새로운 문제를 해결할 수 있도록 하는 접근입니다. 모델이 새로운 상황에서 답을 도출하는 능력을 향상시키는 데 도움을 줍니다. 이 문장에서 말하는 생성적 디스틸레이션 접근은 GRIN MoE가 이 기술을 활용하여 수학 문제를 푸는 데 성공했다는 것을 암시합니다.

따라서 이 문장은 GRIN MoE가 높은 수학적 추론 능력을 보인 것이 단순한 암기 때문이 아니라, 더 나아가 학습한 지식을 바탕으로 창의적으로 문제를 해결하는 능력(생성적 디스틸레이션)의 결과라는 것을 말하고 있습니다. 이는 모델이 새로운 문제나 도전에 직면했을 때도 그 지식을 활용해 추론하고 답을 도출할 수 있다는 것을 의미하므로, 모델의 지능적인 측면을 더 강조하는 내용입니다.

-----

 

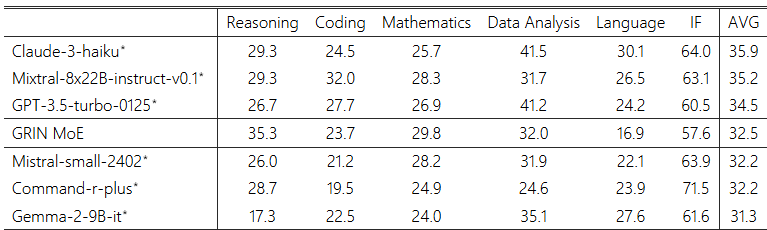
표 4: LiveBench-2024-07-25에서의 GRIN MoE 성능. 모델들은 평균 점수(AVG)를 기준으로 순위가 매겨졌습니다. ∗기준선 결과는 공식 벤치마크에서 참조되었습니다.

 

 

GRIN MoE 응답 논의
GRIN MoE의 응답을 분석한 결과, 몇 가지 흥미로운 관찰을 할 수 있었습니다:

• 복잡한 수학 문제 해결 능력: GRIN MoE는 어려운 수학 문제를 해결할 수 있는 능력을 보입니다. 예를 들어, 질문 4는 모델이 미지의 변수를 포함한 삼각 함수에 대한 대수적 조작을 수행해야 했습니다. 부록 D.4에 나온 것처럼 GRIN MoE는 올바른 답을 제시했을 뿐만 아니라, 필요한 모든 유도 과정을 정확히 제시했습니다. 특히, GRIN MoE는 우리가 테스트한 모델들(Llama3, Phi-3 모델 포함) 중 유일하게 이 질문에 정확하게 답을 한 모델이었습니다.
• 단일 선택 및 다중 선택 문제에 대한 응답: GRIN MoE는 때때로 올바르거나 부분적으로 올바른 답을 제시했지만, 생각의 흐름(chain-of-thought)을 보여주는 프롬프트에서 오타(부록 D.5의 질문 5와 부록 D.9의 질문 9), 누락된 단계(부록 D.7의 질문 7), 또는 오류(부록 D.10의 질문 10 및 부록 D.11의 질문 11)를 포함하는 경우가 있었습니다. 또한 어려운 질문에 대해 GRIN MoE의 출력이 극적으로 변하는 경우도 관찰되었습니다. 이러한 현상은 다른 모델들의 응답에서도 관찰됩니다.
• 힌트를 빠르게 이해하는 능력: 질문 13(부록 D.13 참조)에서, GRIN MoE는 처음에 점 (0,1)이 곡선 y=ln⁡(x+1)+a 위에 있다고 가정하여 잘못된 답을 내놓았습니다. 그러나 곡선과 점 사이의 관계를 강조하는 힌트를 반영한 후, GRIN MoE는 응답을 크게 수정하고 문제를 올바르게 해결했습니다(부록 D.15 참조). 이 질문에서 힌트를 제공한 후 정확한 답을 생성한 것은 Llama3 및 Phi-3 밀집 모델을 포함한 모든 모델 중 GRIN MoE가 유일했습니다.

GRIN MoE와 Phi-3.5-MoE를 비교해본 결과, 서로 다른 응답 패턴이 관찰되었습니다. 부록 E.1 및 E.7에 나온 것처럼, Phi-3.5-MoE는 때때로 생각의 흐름(chain-of-thought) 프롬프트 없이 응답을 생성했지만, GRIN MoE는 모든 14개의 질문에 대해 일관되게 생각의 흐름을 제공했습니다. 또한 부록 E.12와 E.4에 나온 것처럼, Phi-3.5-MoE는 때때로 응답의 끝에서 반복적인 출력을 생성한 반면, GRIN MoE는 모든 14개의 질문에 대해 적절한 결론을 유지했습니다. 이러한 현상은 Phi-3.5 모델의 훈련 초점이 128K 토큰까지의 긴 컨텍스트 처리와 다국어 처리 능력을 포함하고 있기 때문일 수 있다고 추측합니다.

 

게다가 Phi-3.5-MoE가 생성한 답변은 GRIN MoE와 상당히 다릅니다. 14개의 질문 중 동일한 답변을 제공한 것은 단 5개에 불과했습니다. 두 모델 모두 정답을 맞춘 질문에서도 각기 다른 설명을 제공했습니다. 추가로, 두 모델이 질문 13에서 동일한 실수를 했음에도(부록 D.13 및 E.13 참조), GRIN MoE는 제공된 힌트를 빠르게 반영해 질문에 올바르게 답한 반면(부록 D.15 참조), Phi-3.5-MoE는 실패했습니다(부록 E.15 참조).

 

4.4 한계 및 약점
GRIN MoE의 훈련 코퍼스인 Phi-3 데이터는 추론 및 코딩 능력에 중점을 두고 구성되었기 때문에, 모델이 자연어 작업에서 최적이 아닌 성능을 보이는 것을 관찰할 수 있었습니다. 우리는 모델 평가를 위해 2024-07-25에 발표된 LiveBench를 사용하였으며(White et al., 2024), GRIN MoE의 성능을 표 4에 요약했습니다. 여기에는 유사한 평균 점수를 가진 다른 6개의 모델의 성능도 나와 있습니다.

 

이 벤치마크에서 유사한 평균 점수를 가진 기준 모델들과 비교했을 때, GRIN MoE는 추론, 코딩, 수학 작업에서 더 나은 점수를 달성했습니다. 이 결과는 섹션 4.3의 사례 연구와 일치합니다. 반면, GRIN MoE는 자연어 작업에서 매우 낮은 평균 점수(즉, 16.9)를 기록했습니다. 이는 훈련 코퍼스의 한계 때문일 가능성이 있으며, 동일한 코퍼스로 훈련된 다른 모델들도 유사한 문제를 겪는 것을 관찰했습니다.

 

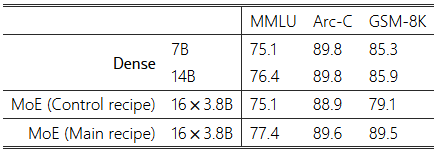
표 5: 반통제 성능 비교. 표 2와 그림 1의 결과와 달리, 여기에서 보고된 성능은 후속 훈련 전의 성능입니다. 자세한 설정은 섹션 5.1에 설명되어 있습니다.

 

5 분석
섹션 3에서 설명한 바와 같이, 우리는 SparseMixer-v2와 부하 균형 손실 적응을 특징으로 GRIN MoE의 훈련 방식을 조정했습니다. 하지만 자원 제한으로 인해 GRIN MoE의 규모에서 각 변수의 영향을 개별적으로 연구할 수 있는 통제된 환경을 설정할 수 없었습니다. 따라서 훈련 방식의 효과를 정량화하기 위해 반통제 비교를 수행했습니다.

 

5.1 반통제 설정
다음 두 가지 훈련 방식을 비교했습니다(메인 방식과 통제 방식):

• 메인 방식은 섹션 3에서 설명한 GRIN MoE 훈련에 사용된 방식입니다.
• 통제 방식은 기존의 MoE 훈련 방식을 닮았으며, 비교를 위해 사용되었습니다. 이 방식은 SparseMixer-v2를 GShard로 교체하고, 전역 부하 균형 손실을 로컬 부하 균형 손실로 대체하며, 몇 가지 하이퍼 파라미터를 수정한 점에서 메인 방식과 다릅니다.

이후 두 가지 방식으로 MoE 모델을 4T 토큰 코퍼스에서 훈련하고, 후속 훈련 없이 동일한 4T 토큰 코퍼스의 상위 집합에서 훈련된 Phi-3 7B 및 14B 모델과 다운스트림 작업에서 비교했습니다.

 

그림 2에서의 통제 실험과 비교했을 때, 통제 방식은 섹션 3.3에서 설명한 전역 부하 균형 손실을 적용하지 않으며, 반면 그림 2의 GShard 기준선은 전역 부하 균형 손실 적응을 적용했습니다.

 

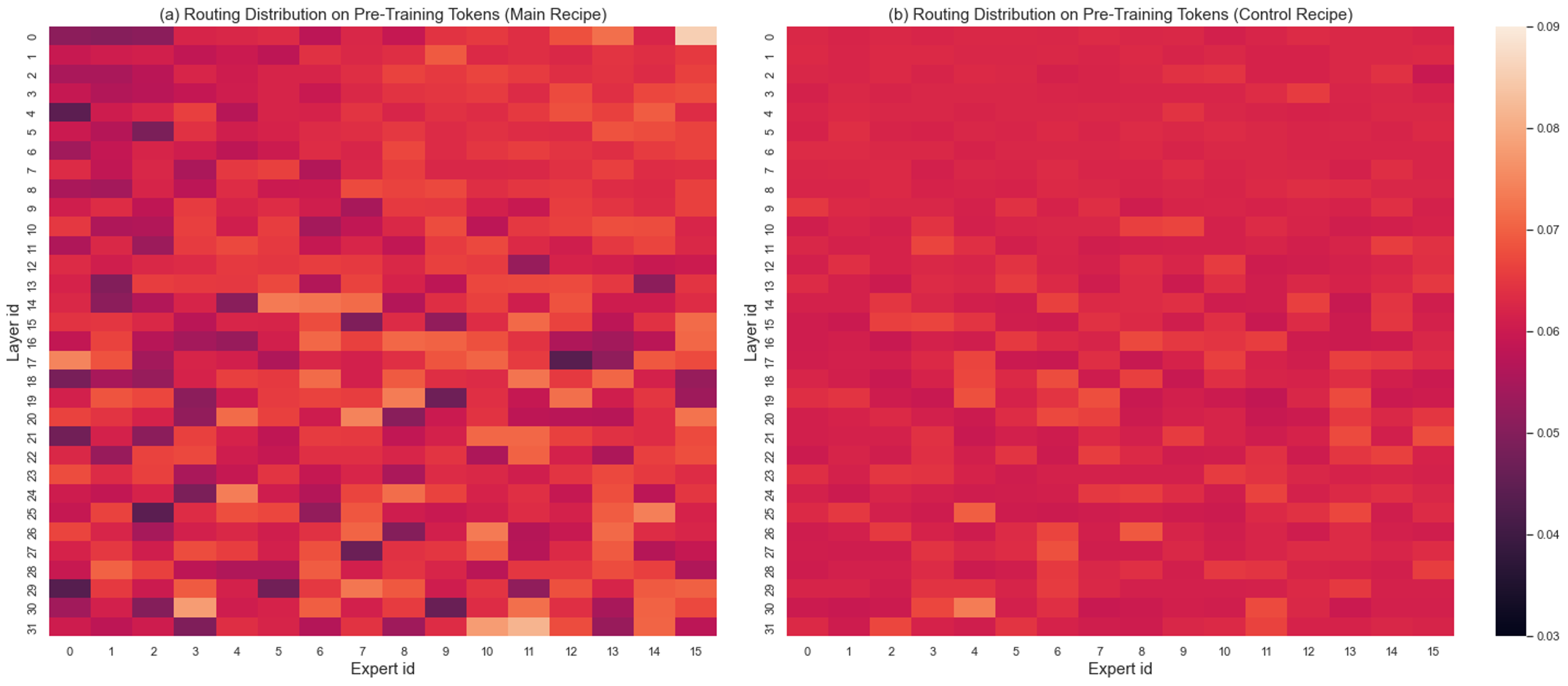
그림 5: 200만 개의 사전 훈련 토큰에 대한 라우팅 분포. 왼쪽 모델은 메인 방식으로 훈련되었으며, 오른쪽 모델은 통제 방식으로 훈련되었습니다. 값은 각 레이어별로 정규화되었습니다. 각 행의 값 합계는 1입니다(완전히 균형 잡힌 로딩은 0.0625의 값을 가집니다).

 

-----

이 설명은 GRIN MoE 모델의 훈련 과정에서 전문가(expert)의 로딩(즉, 전문가의 활성화 비율)이 각 레이어에서 어떻게 분포되는지를 시각화한 것입니다. 이 그림을 분석하는 것은 MoE 모델이 학습하는 동안 전문가들이 얼마나 균등하게 활성화되고 있는지, 그리고 이 균형이 모델 훈련 효율성과 성능에 어떤 영향을 미칠 수 있는지를 이해하는 데 중요한 의미를 가집니다.

조금 더 자세히 설명하자면:

1. 라우팅 분포:
   • 라우팅 분포는 입력 토큰이 여러 전문가 중에서 어떤 전문가에게 할당되었는지를 보여주는 것입니다. 각 전문가의 "로드(부하)"가 얼마나 되는지를 시각화한 것이죠. 만약 전문가들이 균등하게 선택되고 있다면, 모든 전문가가 일정하게 부하를 공유하고 있는 상태입니다.
2. 정규화와 균형:
   • 정규화된 값은 각 레이어별로 계산된 값이 총합이 1이 되도록 만들어진 것입니다. 각 행의 값 합계가 1이라는 것은 각 레이어 내에서 모든 전문가들이 받은 부하를 합쳤을 때 항상 동일하다는 것을 의미합니다.
   • 완전히 균형 잡힌 로딩은 각 전문가가 동일한 비율의 부하를 가지는 경우를 의미합니다. 예를 들어, 레이어에 16개의 전문가가 있다면, 각 전문가가 약 0.062 (즉, 1/16)의 부하를 가져야 완벽하게 균형 잡혔다고 볼 수 있습니다.
3. 왼쪽(메인 방식)과 오른쪽(통제 방식) 모델 비교:
   • **왼쪽 모델(메인 방식)**은 새로운 SparseMixer-v2와 전역 부하 균형 손실 방식을 사용하여 훈련된 모델입니다.
   • **오른쪽 모델(통제 방식)**은 기존 MoE 훈련 방식에 기반하여 훈련된 모델입니다.
   • 그림에서 왼쪽 모델의 경우, 오른쪽 모델보다 전문가의 부하가 더 불균형하게 분포되었다고 볼 수 있습니다. 이는 모든 전문가들이 동일한 양의 작업을 수행하지 않았다는 것을 의미합니다.
4. 의미와 중요성:
   • 균형 잡힌 로딩의 중요성: 전문가들이 균등하게 활성화되면, 모델 자원을 효율적으로 사용할 수 있습니다. 즉, 모든 전문가가 고르게 활용되기 때문에 학습 과정에서 특정 전문가에게 과도한 부하가 걸리지 않으며, 이는 모델의 효율성을 높이고 학습된 결과의 일반화를 도울 수 있습니다.
   • 불균형의 장점: 반면, 불균형한 로딩은 특정 전문가가 특정 유형의 입력에 대해 전문화된다는 것을 의미할 수 있습니다. 이렇게 되면 모델 내의 전문가들이 서로 다른 유형의 작업에 특화되도록 학습될 수 있으며, 이는 모델의 성능을 특정 문제에 대해 더 높일 수 있는 장점이 있습니다. 메인 방식으로 훈련된 모델이 더 불균형한 로딩을 가지고 있다는 것은, SparseMixer-v2와 전역 부하 균형 손실을 적용했을 때 전문가들이 더 다양한 입력에 대해 특화될 수 있음을 나타냅니다.

따라서, 이 그림을 통해 알 수 있는 것은 메인 방식의 훈련이 통제 방식보다 전문가들이 더 전문화되도록 하고, 이로 인해 모델의 성능에 긍정적인 영향을 미칠 수 있다는 점입니다.

-----

 

5.2 다운스트림 성능
결과는 표 5에 나와 있습니다. 통제 방식으로 훈련된 모델은 7B 밀집 모델의 성능과 일치하는 반면, 메인 방식은 더 효과적이어서 14B 밀집 모델의 성능과 일치하는 모델을 생성했습니다. 이 효과는 SparseMixer-v2와 적응형 손실 수정 덕분이라고 볼 수 있습니다.

 

5.3 라우팅 분석
메인 방식과 통제 방식으로 훈련된 모델의 라우팅 분포를 분석했습니다. 각 레이어에서 각 전문가가 서로 다른 은닉 상태에 의해 선택된 횟수를 라우팅 분포로 계산했습니다.

 

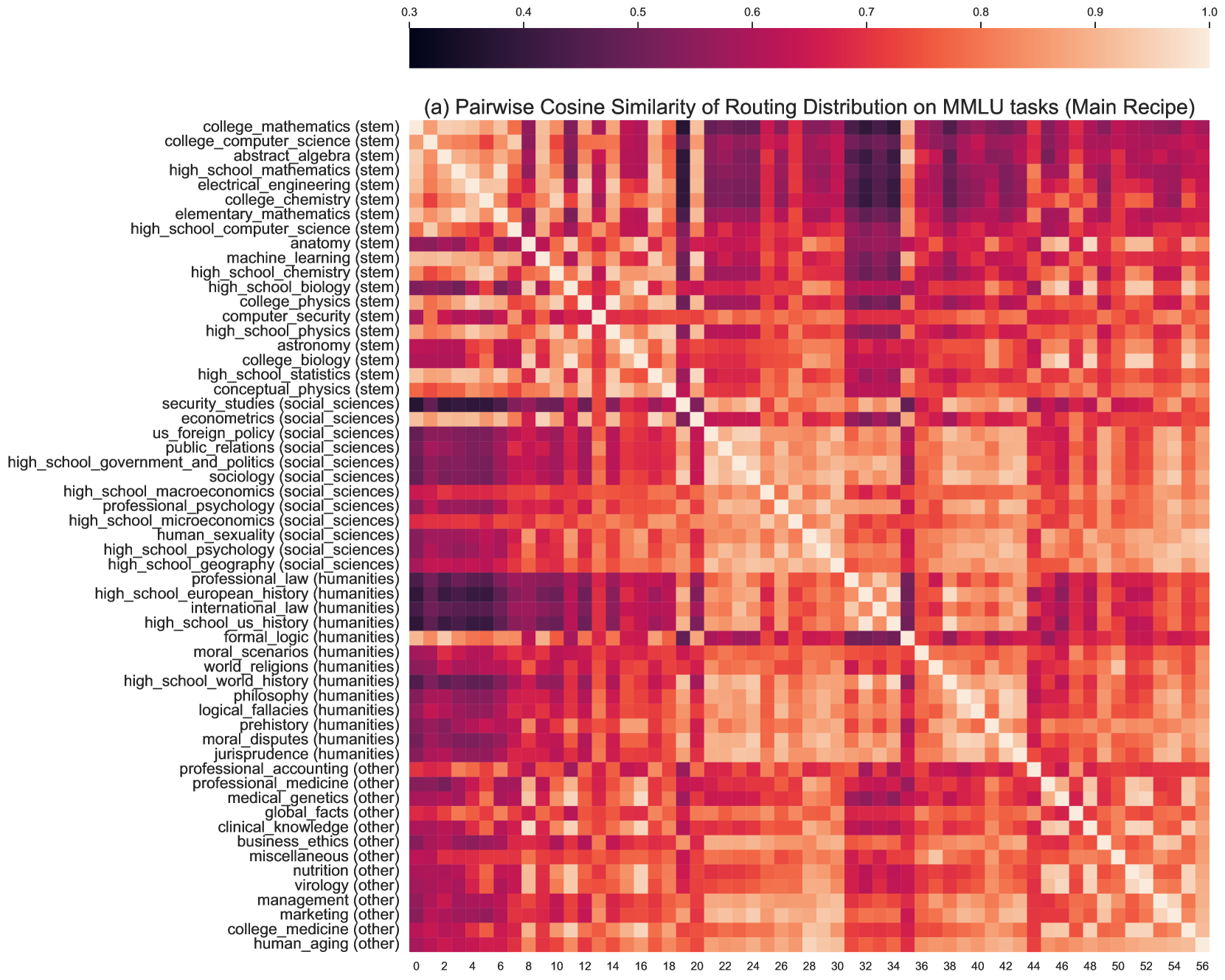
그림 6 (a): 메인 방식으로 훈련된 모델의 MMLU 57개 작업 간 MoE 라우팅 분포 유사성. 어두운 색은 유사성이 낮음을 의미합니다. x축과 y축은 동일한 작업 순서를 가집니다.

 

사전 훈련 데이터에서의 MoE 라우팅
사전 훈련 데이터셋에서의 라우팅 분포를 분석하기 위해 사전 훈련 데이터셋에서 임의로 200만 개의 토큰을 선택하고, 그림 5에서 전문가 로딩 분포를 시각화했습니다. 먼저 두 방식의 모든 레이어에서 전문가 로딩이 적절하게 균형 잡혀 있음을 확인할 수 있습니다. 그림 5에서 최대 값은 0.09로, 이는 완전히 균형 잡힌 전문가 로딩(0.0625)의 약 1.44배입니다. 비교적 메인 방식으로 훈련된 모델이 통제 방식보다 덜 균형 잡혀 있는 것을 관찰할 수 있습니다.

 

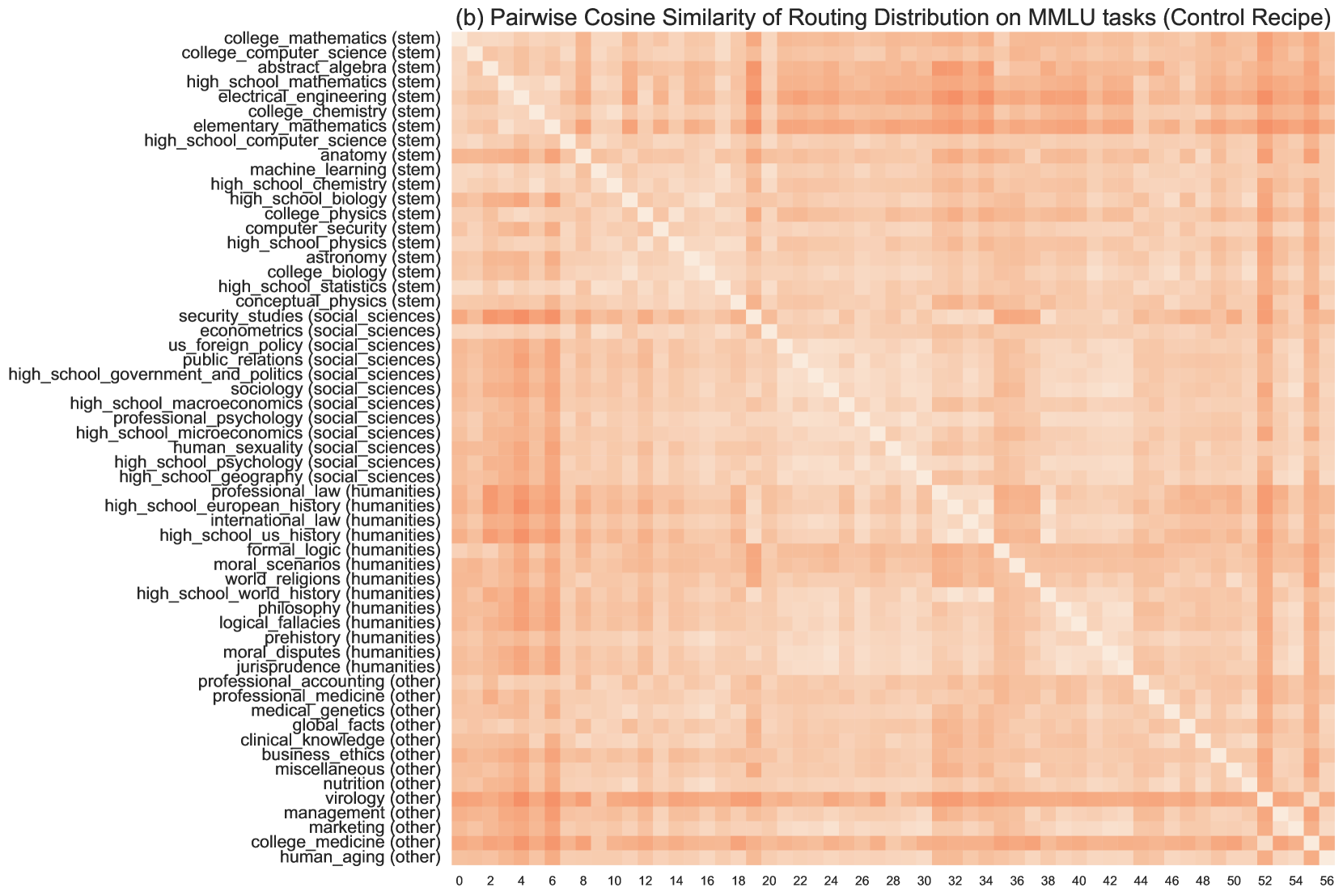
그림 6 (b): 통제 방식으로 훈련된 모델의 MMLU 57개 작업 간 MoE 라우팅 분포 유사성. 이 그림은 그림 6 (a)와 동일한 설정과 색상 막대를 공유합니다.

 

다른 MMLU 작업에서의 MoE 라우팅
다음으로, 서로 다른 전문가가 도메인 특화 정보를 포함하는지 실험적으로 검증했습니다. 먼저 MMLU의 57개 작업 간의 라우팅 분포를 비교했습니다. 각 작업에 대해 5번의 샷을 가진 24개의 프롬프트를 샘플링했습니다. 각 작업의 라우팅 분포는 16(레이어당 전문가) × 32(레이어) 차원의 벡터입니다(총 전문가 수). 그런 다음 다른 작업 간의 라우팅 분포의 코사인 유사성을 계산하고, 이를 그림 6 (a)와 6 (b)에 히트맵으로 시각화했습니다. 여기서 57개의 작업을 메타 데이터에 따라 4개의 범주로 그룹화했습니다. 사용한 메타 데이터는 Hendrycks et al. (2021)에서 제공된 것입니다.

 

우리의 메인 방식으로 훈련된 MoE는 그림 6 (a)에 나와 있으며, STEM 범주가 사회과학 및 인문학과 명확한 경계를 가지고 있음을 확인할 수 있습니다. 또한 사회과학 및 인문학의 두 개의 특이점(즉, 계량 경제학과 형식 논리학)이 STEM 범주와 더 높은 유사성을 가지는 것도 합리적입니다. 이는 서로 다른 작업 간에 라우팅 분포가 크게 다를 수 있음을 나타냅니다. 통제 방식으로 훈련된 모델(그림 6 (b) 참조)에서는 작업 간 라우팅 분포가 유사하게 나타났습니다.

 

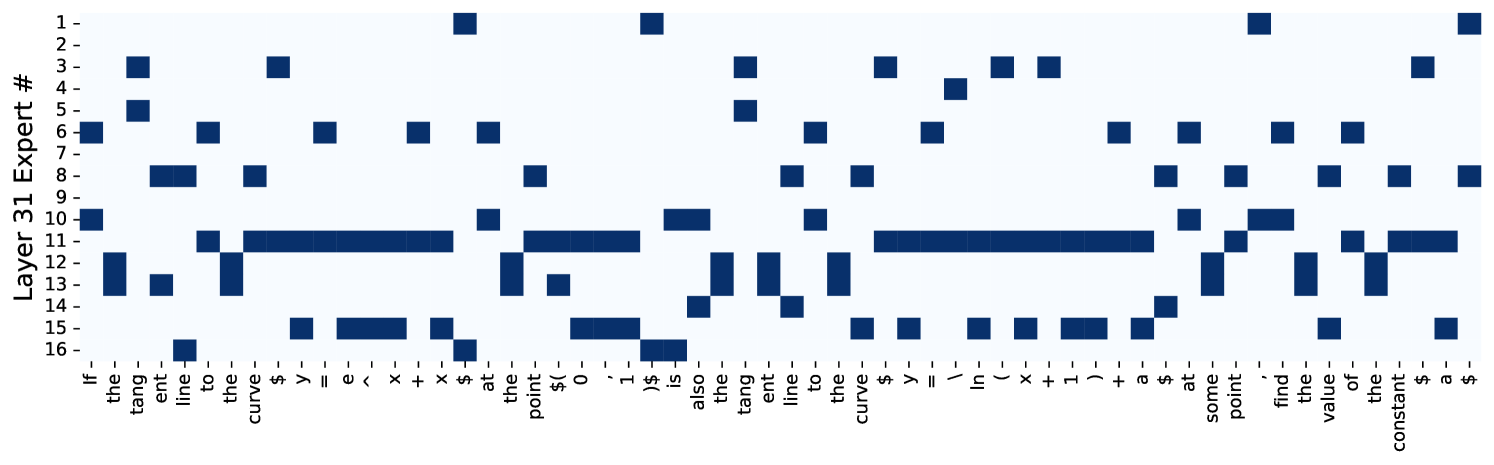
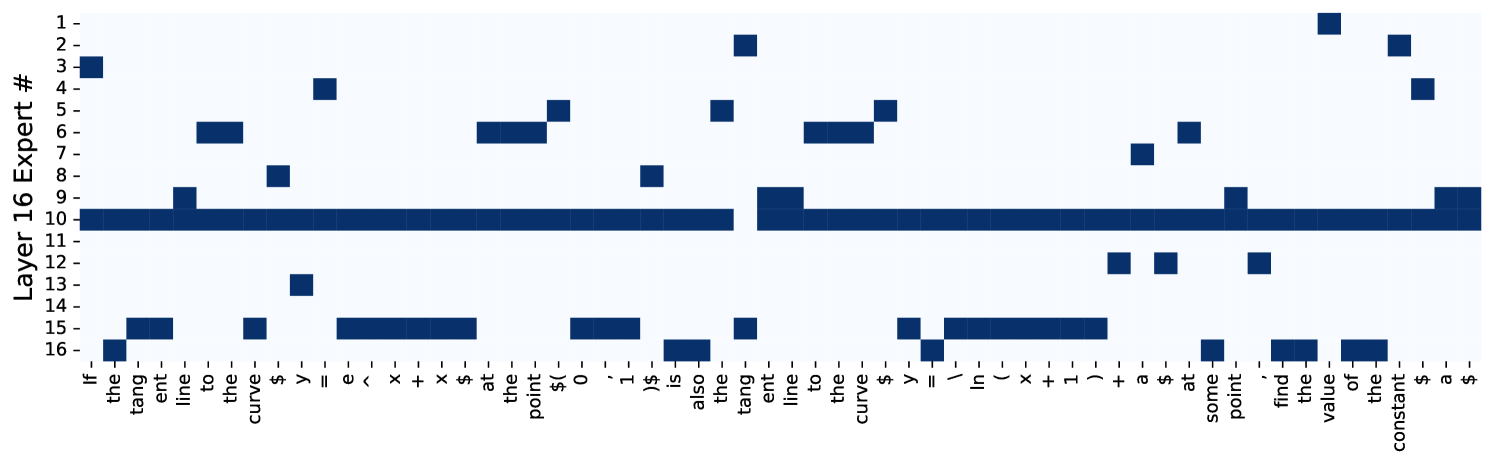
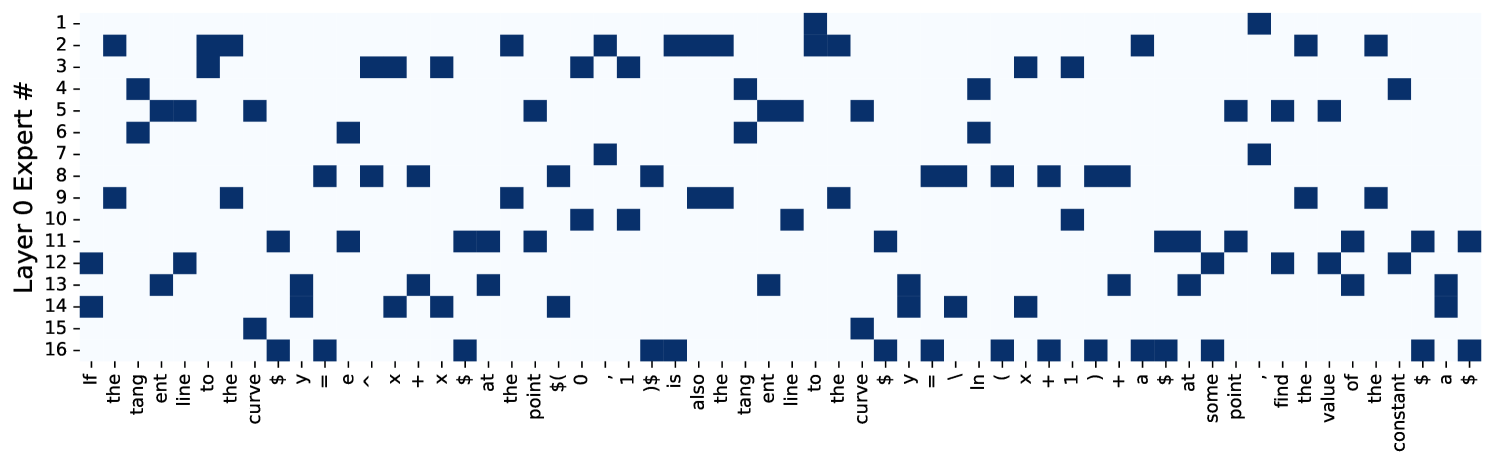
그림 7: 메인 방식으로 훈련된 MoE의 사례 연구. 서로 다른 레이어에서 서로 다른 위치에서 전문가가 선택되는 방식을 시각화했습니다. 최근 발표된 대학 입학 시험에서 한 질문을 선택해 사례 연구를 진행했으며, 추가 정보는 부록 D.15에 있습니다.

 

MoE 라우팅의 사례 연구
이 분석은 메인 방식으로 훈련된 MoE 모델을 사용합니다. 그림 7에 나와 있듯이, 레이어마다 라우팅 분포가 다릅니다. 아래쪽(얕은) 레이어에서는 가장 균형 잡힌 전문가 분포를 가지고 있습니다. 중간 레이어에서는 전문가 10과 15가 다른 전문가들보다 더 많이 선택됩니다. 최종(깊은) 레이어에서는 중간 레이어보다 더 균형 잡힌 상태가 됩니다. 이러한 결과는 MoE 라우팅 분포가 문맥, 단어, 위치 등의 정보와 관련이 있음을 나타냅니다.

 

우리의 연구는 GRIN MoE의 전문가 네트워크들이 고도로 전문화되고 이질적인 전문성을 개발했다는 가설을 검증하는 것 같습니다. Wei et al. (2024)이 지적한 바와 같이, 이러한 전문가들은 모델의 능력을 향상시키는 데 기여할 가능성이 있습니다.

 

6 결론
본 논문에서는 새로운 MoE 모델인 GRIN MoE와 이를 훈련하기 위한 모델 훈련 기술(즉, 희소 역전파와 모델 병렬 구성)에 대해 자세히 설명했습니다. 동일한 사전 훈련 코퍼스에서 훈련된 밀집 모델과 비교했을 때, GRIN MoE는 MoE의 놀라운 확장 가능성을 보여줍니다. 우리는 또한 GRIN MoE의 개발 과정에서 얻은 관찰 결과와 통찰력을 요약하여 MoE 훈련에 대한 이해를 심화하는 것을 목표로 했습니다. 통제된 실험과 반통제 실험을 통해, 경사 추정 방법과 모델 병렬화 전략이 보조적 적응과 함께 모델 훈련을 크게 향상시키는 방법을 입증했습니다.

 

앞으로 해결해야 할 중요한 질문이 많이 남아 있습니다. 예를 들어, MoE 모델의 훈련과 추론은 알고리즘과 엔지니어링 구현 모두에 도전을 제시합니다. 또한, 소프트맥스가 원래 argmax 연산을 근사하기 위해 설계되었기 때문에, 이는 topk를 샘플링으로 근사화하는 데 새로운 도전을 제시합니다. 우리는 이러한 문제에 대한 해결책을 더 탐구할 계획이며, 희소성을 강화하고 효율적인 계산 및 확장 방법을 개발하여 최첨단 MoE 모델링을 발전시키는 데 중점을 두고자 합니다.

 

감사의 말
우리는 계산 인프라 지원을 제공해준 마이크로소프트 엔지니어링 팀에 감사를 표합니다. 또한, 사전 훈련 데이터를 제공해준 Mojan Javaheripi, Suriya Gunasekar, Sébastien Bubeck에게도 감사를 표합니다. 추가로, Abhishek Goswami, Alessandro Sordoni, Amin Saied, Ammar Ahmad Awan, Anh Nguyen, Benjamin Sorscher, Caio César Teodoro Mendes, Chandan Singh, Colin White, Eric Xihui Lin, Gustavo de Rosa, Hanxiao Liu, Joe Mayer, Liliang Ren, Marko Radmilac, Michael Santacroce, Michael Wyatt, Olatunji Ruwase, Philipp Witte, Russell Hewett, Swadheen Shukla, Xia Song, Yadong Lu, Yang Liu, Yuanzhi Li, Yunan Zhang, Zichong Li, Zhen Zheng에게 그들의 도움과 유익한 토론에 대해 감사를 드립니다.

 

2409.12136v1 (1).pdf

2.34MB