https://research.google/blog/understanding-transformer-reasoning-capabilities-via-graph-algorithms/
Understanding Transformer reasoning capabilities via graph algorithms
Conclusion We provide a comprehensive evaluation of transformer models’ graph reasoning capabilities, shedding light on their effectiveness across diverse graph reasoning tasks. By introducing a novel representational hierarchy, the study distinguishes b
research.google
우리는 트랜스포머 모델의 그래프 추론 능력에 대한 포괄적인 평가를 제공하고, 이들이 종종 더 도메인 특화된 그래프 신경망보다 뛰어남을 입증합니다.
트랜스포머는 2017년 구글에서 도입한 범용 순차적 딥러닝 아키텍처입니다. 최근에, 그리고 놀랍게도, 트랜스포머는 연결성(예: "노드 A에서 노드 B로 가는 경로가 있습니까?"), 최단 경로("노드 A에서 노드 B로 가기 위해 얼마나 많은 간선을 거쳐야 합니까?"), 그리고 사이클 검사("그래프에 사이클이 있습니까, 예: A → B, B → C, C → A와 같은 간선?")과 같은 그래프 기반 알고리즘 작업을 학습하는 데 능숙하다는 것을 암시하고 있습니다.
왜 이것이 놀라운 일일까요? 메시지 패싱 신경망(MPNN)과 달리, MPNN의 파라미터는 입력 그래프의 구조를 명시적으로 인코딩하는 반면, 트랜스포머는 언어 작업으로 가장 잘 알려진 범용 아키텍처입니다. 트랜스포머의 핵심은 입력 단어/토큰 간의 연관성을 인코딩하는 계산 비용이 많이 드는 자기 주의(self-attention) 메커니즘으로, 그래프를 위해 명시적으로 설계된 것이 아닙니다. 따라서 트랜스포머 기반의 신경망이 실증적으로 엄청난 진전을 이루었음에도 불구하고, 현실적인 시나리오에서 그들의 알고리즘적 추론 능력에 대한 이론적 이해는 여전히 부족합니다. 어떤 아키텍처가 어떤 실제 작업에 최적인지 아는 것은, 수작업으로 선택된 작업을 통해 새로운 아키텍처를 정의하고 평가하는 데 드는 시간을 훨씬 줄이고, 아키텍처 결정의 트레이드오프에 대한 훨씬 더 나은 이해를 의미합니다.
“그래프 알고리즘을 통한 트랜스포머 추론 능력 이해하기”에서, 우리는 이론적 및 실증적 관점에서 트랜스포머를 사용한 그래프 추론 문제에 대한 광범위한 연구를 수행합니다. 우리는 트랜스포머가 병렬 처리 가능한 작업(예: 연결성)을 매우 파라미터 효율적인 방식으로 해결할 수 있으며, 장거리 종속성 분석이 필요한 작업에서 그래프 신경망(GNN)을 능가함을 발견했습니다. 또한, 여러 현실적인 파라미터 스케일링 체계에서 트랜스포머의 추론 능력을 형식화한 새로운 그래프 추론 작업의 표현 계층을 소개합니다.
실험
MPNN은 그래프 구조를 존중하는 함수를 학습하도록 명시적으로 설계된 맞춤형 신경 아키텍처인 반면, 트랜스포머는 훨씬 더 일반적입니다. 그러나 트랜스포머와 MPNN은 유사한 머신러닝 프레임워크를 사용하여 그래프 알고리즘 문제를 해결하도록 학습시킬 수 있습니다.
실험의 실증적 부분에서는 트랜스포머가 MPNN과 유사한 방식으로 그래프 작업을 인코딩할 수 있는지, 그리고 그렇다면 더 효율적으로 수행할 수 있는지를 조사했습니다.
이를 테스트하기 위해, 우리는 그래프 작업을 트랜스포머 입력으로 인코딩했습니다. 그래프 인스턴스(노드와 간선 포함)와 쿼리(노드 𝑣2와 𝑣4가 연결되어 있는지 여부를 결정)를 주어진 상황에서, 각 노드 ID를 이산 토큰으로 인코딩하고(LLM이 단어를 토큰으로 매핑하는 방식과 유사하게) 각 간선을 토큰 쌍으로 인코딩했습니다. 그런 다음 문제를 노드 토큰 목록, 간선 토큰 목록, 그리고 쿼리의 토큰 인코딩으로 구성된 리스트로 인코딩했습니다.
그래프 추론 작업 인스턴스(여기서는 그래프 연결성)가 트랜스포머 입력으로 어떻게 임베딩되는지.
트랜스포머와 MPNN이 그래프의 구조적 분석을 위한 유일한 머신러닝 접근법이 아니기 때문에, 우리는 다양한 다른 GNN 및 트랜스포머 기반 아키텍처의 분석 능력도 비교했습니다. GNN의 경우, 트랜스포머와 MPNN을 그래프 컨볼루셔널 네트워크(GCN) 및 그래프 동형 네트워크(GIN)와 같은 모델과 비교했습니다.
추가적으로, 우리는 훨씬 더 큰 언어 모델과도 트랜스포머를 비교했습니다. 언어 모델은 역시 트랜스포머이지만, 파라미터 수가 수십 배 더 많습니다. 우리는 트랜스포머를 "Talk Like a Graph"에서 설명한 언어 모델링 접근법과 비교했습니다. 이 접근법은 그래프를 텍스트로 인코딩하고, 관계를 설명하기 위해 자연어를 사용하며, 입력 그래프를 추상적인 토큰 집합으로 취급하지 않습니다.
우리는 훈련된 언어 모델에게 다양한 프롬프트 접근법을 사용하여 여러 검색 작업을 해결하도록 요청했습니다:
- 제로샷(Zero-shot): 단일 프롬프트만 제공하고 추가적인 힌트 없이 해결책을 요청합니다.
- 퓨샷(Few-shot): 해결된 프롬프트-응답 쌍의 여러 예시를 제공한 후 모델에게 작업을 해결하도록 요청합니다.
- 체인-오브-쏘트(CoT, Chain-of-thought): 퓨샷과 유사하게 여러 예시를 제공하지만, 각 예시는 프롬프트, 응답, 그리고 작업을 해결하기 전에 설명을 포함합니다.
- 제로샷 CoT: 추가적인 작업 예시를 컨텍스트로 포함하지 않고, 모델에게 작업을 해결하면서 그 과정을 보여달라고 요청합니다.
- CoT-bag: 관련 정보를 제공받기 전에 LLM에게 그래프를 구성하도록 요청합니다.
실험의 이론적 부분에서는 트랜스포머가 소형 모델로 해결할 수 있는 작업을 평가하기 위해 작업 난이도 계층을 만들었습니다.
우리는 노드 수, 간선 수, 간선 존재 여부, 노드 차수, 연결성, 노드 연결성(무향 그래프의 경우), 사이클 검사, 최단 경로와 같이 제한된 크기의 무향 및 무가중 그래프에 적용되는 그래프 추론 작업만을 고려했습니다.
이 계층에서 우리는 그래프 작업의 난이도를 깊이(트랜스포머의 자기 주의 층 수, 순차적으로 계산됨), 너비(각 그래프 토큰에 사용되는 벡터의 차원), 빈 토큰의 수, 그리고 세 가지 다른 유형을 기준으로 분류했습니다:
- 검색 작업(Retrieval tasks): 쉬운, 지역 집계 작업.
- 병렬 처리 가능한 작업(Parallelizable tasks): 병렬 연산으로 크게 이점을 얻는 작업.
- 검색(Search): 병렬 연산으로부터 제한된 이점을 얻는 작업.
결과
실험적 결과
소형 모델(~60M 파라미터)을 특화된 데이터로 훈련시킨 경우, 트랜스포머는 타겟 훈련 없이도 훨씬 더 큰 LLM을 능가하는 성능을 보입니다(아래의 바 차트 참조). 또한, 트랜스포머의 알고리즘적 추론 능력은 적은 샘플과 적은 파라미터로도 향상될 수 있습니다.
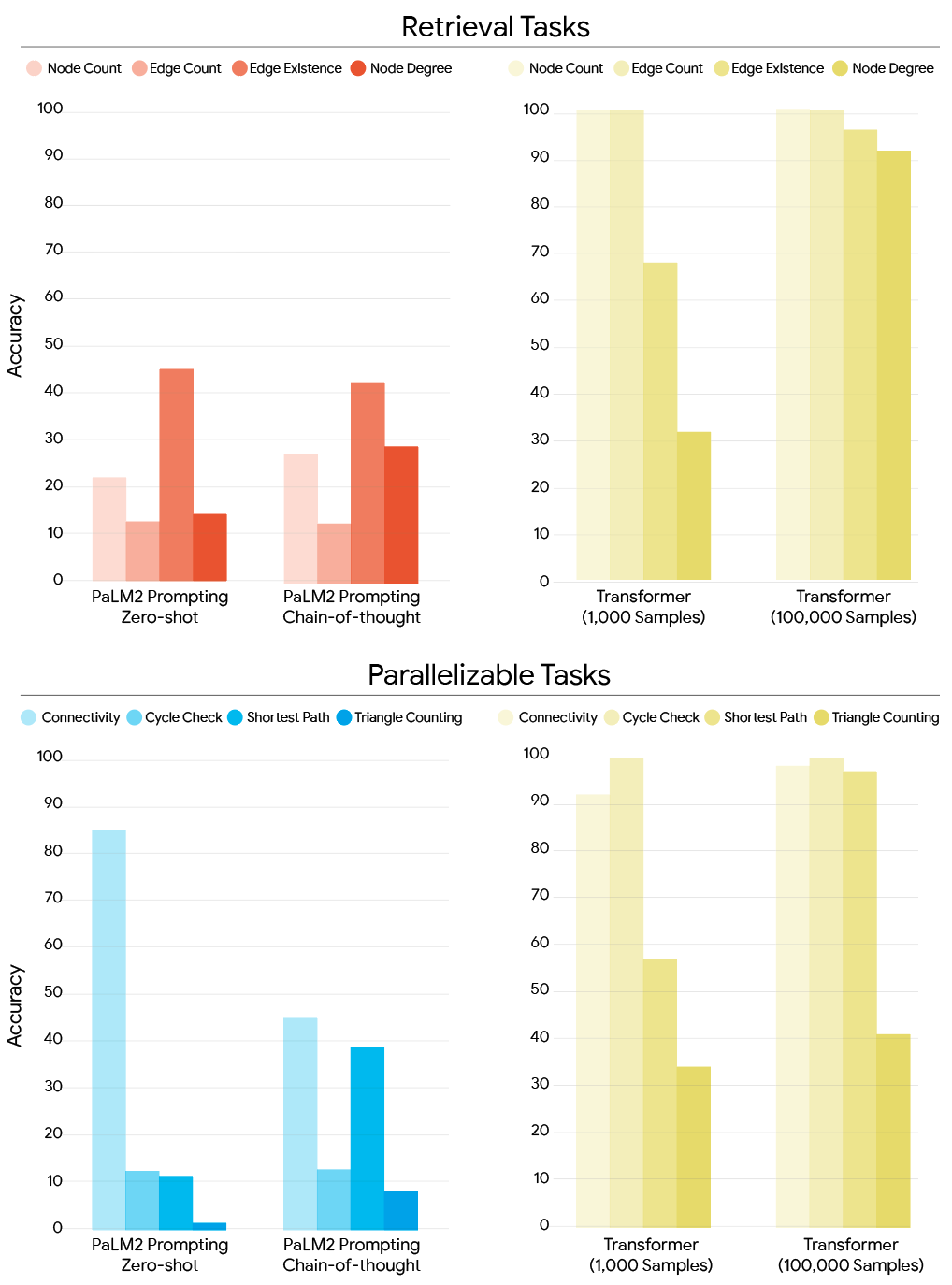
모델 훈련 방식에 따른 모든 검색 작업(상단) 및 병렬 처리 가능 및 검색 작업(하단)에서의 정확도 비교, 프롬프트된 PaLM2 LLM(왼쪽)과 훈련된 트랜스포머(오른쪽) 비교.
아래에 나타난 바와 같이, MPNN은 "로컬" 작업에서 더 좋은 성과를 보입니다. 로컬 작업은 이웃 노드에 대한 정보를 집계하는 작업으로, 많은 "추론 홉"을 필요로 하지 않습니다. 1K 샘플 또는 100K 샘플로 훈련된 경우 모두 MPNN은 노드 차수(노드에 인접한 간선의 최대 수) 및 사이클 검사와 같은 로컬 작업에서 더 높은 정확도를 보입니다.
반면, 트랜스포머는 "글로벌" 작업에서 더 나은 성능을 보입니다. 글로벌 작업은 정보가 그래프 인스턴스 전반에 걸쳐 전파되어야 하는 작업입니다. 예를 들어, 그래프 연결성은 글로벌 작업의 예시로, 두 노드가 그래프에서 멀리 떨어져 있을 수 있기 때문입니다.

아키텍처별 작업 성능, 노드 차수, 사이클 검사 및 연결성 비교.
이 결과는 소형 샘플 체계와 대형 샘플 체계 간의 차이가 트랜스포머에서는 훨씬 더 크다는 것을 보여주며, GNN은 100K 샘플로 훈련된 경우 트랜스포머의 성능에 근접하지 못한다는 것을 나타냅니다.
신경망을 훈련할 때 중요한 두 가지 동역학: 용량과 학습 가능성.용량은 신경망 아키텍처의 근본적인 한계를 나타냅니다. 즉, 용량은 신경망 아키텍처가 표현할 수 있는 수학적 함수의 종류를 결정합니다. 학습 가능성은 이러한 함수가 상대적으로 적은 수의 훈련 샘플로 실제로 학습될 수 있는지를 묻는 질문입니다. 특정 유형의 해결책에 대해 아키텍처가 긍정적인 귀납적 편향을 가지고 있다고 말하는 것은, 적은 샘플로도 해당 해결책을 향해 나아가는 경향이 있다는 의미입니다.
이 프레임워크에서 트랜스포머와 MPNN 결과를 이해해보면, GNN은 그래프 작업에 대해 확실히 더 나은 귀납적 편향을 가지고 있다는 것을 알 수 있습니다. 이는 데이터가 부족한 환경에서 더 우수한 성과를 보임으로써 분명히 나타납니다. 반면, 트랜스포머가 더 큰 데이터셋에서 성공한 것은 GNN이 용량에 의해 제한될 수 있다는 것을 시사합니다. 이는 더 많은 데이터로도 해결할 수 없는 근본적인 모델의 한계를 반영하는 결과입니다.
이론적 결과
우리는 두 아키텍처의 용량 또는 표현 능력을 대비하는 이론적 결과를 통해 실험적 결과를 뒷받침했습니다. 이전 연구에서는 트랜스포머가 병렬 알고리즘을 시뮬레이션할 수 있다는 것을 보여주었으며, MPNN과 같은 다른 모델은 글로벌 연결이 부족하여 제한된다고 밝혔습니다. 우리의 작업 난이도 계층을 사용하여, 트랜스포머가 병렬 처리 가능한 작업에 대해 훨씬 더 큰 표현 능력을 가지고 있고, 이를 로그 깊이와 제한된 너비(즉, 모델의 너비는 그래프 토큰 수 N에 비해 훨씬 느리게 성장하는 어떤 양 m, 예: m ≤ N^0.1)로 해결할 수 있음을 보여주었습니다. 반면, 어떤 MPNN도 이러한 작업을 해결할 수 없으며, 계산적으로나 파라미터 수 면에서 훨씬 더 커야만 가능합니다.
-----
깊이(log depth)와 너비(bounded width)의 의미
- 로그 깊이(logarithmic depth)
트랜스포머가 병렬 처리 작업을 해결하는 데 필요한 깊이가 로그 함수처럼 증가한다는 의미입니다. 예를 들어, 그래프에 노드 수가 N이라면, 트랜스포머의 "깊이"는 log(N) 만큼만 필요하다는 것입니다. 즉, 그래프 크기가 커져도 트랜스포머의 학습 깊이가 상대적으로 느리게 증가하여 효율적으로 처리할 수 있습니다. 이는 트랜스포머가 병렬 처리 가능한 작업에서 상대적으로 적은 계산량으로 해결할 수 있음을 의미합니다. - 제한된 너비(bounded width)
트랜스포머 모델의 너비는 그래프의 토큰 수인 N에 비해 훨씬 느리게 증가합니다. 구체적으로, m ≤ N^0.1로 표현될 수 있습니다. 여기서 m은 모델의 너비를 의미하고, N은 그래프의 토큰 수입니다. 즉, 그래프 크기가 커질수록 모델의 너비는 천천히 증가하여, 메모리나 계산 자원 소모를 최소화할 수 있습니다. 이는 모델이 그래프 크기에 비례해 급격히 커지지 않고, 상대적으로 적은 자원으로 큰 그래프를 처리할 수 있다는 점에서 유리합니다.
m ≤ N^0.1는 이론적인 표현으로, 실험적으로 확인된 특정 사실이라기보다는 트랜스포머의 수학적 특성을 설명하기 위한 공식입니다. 이론적으로 트랜스포머는 그래프 크기(N)가 커져도 모델의 너비가 천천히 증가한다는 특성을 가짐을 나타냅니다.
-----
우리는 또한 검색 작업이 단일 층 트랜스포머 모델로 해결 가능하고, 병렬 처리 가능한 작업은 로그 깊이로 쉽게 해결할 수 있음을 발견했습니다(즉, 트랜스포머의 깊이는 그래프의 노드 수에 대해 로그적으로 스케일링됨). 검색 작업도 로그 깊이로 해결할 수 있지만, 파라미터 효율적인 방식으로는 불가능합니다.

작업 난이도 계층을 시각화한 것, 여기서 검색, 병렬, 검색 작업은 이를 해결하기 위한 트랜스포머의 복잡성에 따라 조직됩니다.
이 결과는 트랜스포머가 연결성에서 왜 훨씬 더 좋은 성과를 보이는지 설명합니다. GNN과 달리, 모델의 크기(깊이와 파라미터 수 측면)는 입력 그래프의 크기와 함께 빠르게 증가할 필요가 없습니다.
결론
우리는 트랜스포머 모델의 그래프 추론 능력에 대해 포괄적인 평가를 제공하며, 다양한 그래프 추론 작업에서 그들의 효율성을 밝혀냈습니다. 새로운 표현 계층을 도입함으로써, 이 연구는 검색, 병렬 처리 가능, 검색 추론 작업을 구분하고, 다양한 수준의 세분화에서 트랜스포머의 성능에 대한 통찰을 제공합니다. 실험적 조사에서는 트랜스포머가 그래프 기반 추론 문제에서 강력한 성과를 보이며, 종종 전문화된 그래프 모델을 능가하거나 일치하는 결과를 나타냄을 보여줍니다. 또한, 이 연구는 트랜스포머가 글로벌 그래프 패턴을 효과적으로 포착하는 뛰어난 능력을 강조하며, 이는 글로벌 그래프 구조와 관련된 작업을 해결하는 데 중요한 요소인 장기 종속성을 이해하는 데 중요한 역할을 합니다. 전반적으로, 이 작업은 트랜스포머의 근본적인 추론 능력을 반영하는 정밀한 표현 트레이드오프를 분명히 하며, 이러한 능력을 정량화하는 데 사용된 작업들이 샘플 효율적이고 파라미터 효율적인 방식으로 실제로 학습 가능한 것임을 입증합니다.
감사의 말씀
이 연구는 Google의 동료들과 협력하여 진행되었으며, Ethan Hall, Anton Tsitsulin, Mehran Kazemi, Bryan Perozzi, Jonathan Halcrow, Vahab Mirrokni의 도움이 있었습니다.
라벨:
알고리즘 및 이론
데이터 마이닝 및 모델링
'Article' 카테고리의 다른 글
| 거의 2,000년 동안 읽히지 않았던 불에 탄 두루마리에서 해독된 첫 단어들 (1) | 2025.02.09 |
|---|---|
| o1 isn’t a chat model (and that’s the point) (4) | 2025.01.15 |
| Extending video masked autoencoders to 128 frames (1) | 2024.12.19 |
| Security for Data Privacy in Federated Learning with CUDA-Accelerated Homomorphic Encryption in XGBoost (1) | 2024.12.19 |
| Satellite powered estimation of global solar potential (1) | 2024.12.18 |

