https://arxiv.org/abs/2411.03884
Polynomial Composition Activations: Unleashing the Dynamics of Large Language Models
Transformers have found extensive applications across various domains due to the powerful fitting capabilities. This success can be partially attributed to their inherent nonlinearity. Thus, in addition to the ReLU function employed in the original transfo
arxiv.org
초록(Abstract)
Transformer는 강력한 적합(fitting) 능력 덕분에 다양한 분야에서 폭넓게 활용되고 있다. 이러한 성공은 부분적으로 Transformer가 지니고 있는 비선형성(inherent nonlinearity)에 기인한다. 따라서 원래 Transformer 아키텍처에서 사용된 ReLU 함수뿐만 아니라, 연구자들은 GeLU, SwishGLU와 같은 대체 모듈들을 탐구하여 비선형성을 강화하고 표현 능력(representational capacity)을 확장하려 하였다.
본 논문에서는 Transformer의 동역학(dynamics)을 최적화하기 위해 고안된 새로운 범주의 다항식 조합 활성화 함수(polynomial composition activations, PolyCom)를 제안한다. 이론적으로 우리는 PolyCom에 대한 포괄적인 수학적 분석을 제공하며, 다른 활성화 함수와 비교했을 때 PolyCom이 가지는 표현력과 효율성을 강조한다. 특히, PolyCom을 포함한 네트워크가 최적 근사율(optimal approximation rate)을 달성함을 보이며, 이는 Sobolev 공간에서 일반적인 매끄러운 함수(smooth functions)를 근사하는 데 PolyCom 네트워크가 최소한의 파라미터만 필요함을 의미한다.
실험적으로는 대규모 언어모델(large language models, LLMs)의 사전학습(pre-training) 구성에서, 밀집(dense) 및 희소(sparse) 아키텍처 모두를 대상으로 검증하였다. 기존의 활성화 함수를 PolyCom으로 대체함으로써, LLM이 데이터 내 고차 상호작용(higher-order interactions)을 포착할 수 있게 하여 정확도와 수렴 속도(convergence rates) 측면에서 성능을 향상시켰다. 광범위한 실험 결과는 제안 기법의 효과성을 입증하며, 다른 활성화 함수 대비 상당한 개선을 보여준다.
코드는 https://github.com/BryceZhuo/PolyCom 에서 확인할 수 있다.

그림 1 설명
훈련 손실(training loss), 검증 퍼플렉서티(validation perplexity, PPL), 그리고 10억(1B) 파라미터 규모의 밀집 모델에서의 다운스트림 성능 비교. 여기서는 SwiGLU, GELU, ReLU, PolyReLU, PolyNorm 등 다양한 활성화 함수를 적용한 모델들을 비교하였다. 결과는 PolyReLU와 PolyNorm을 사용하는 모델이 더 낮은 훈련 손실과 검증 PPL을 보이며, 다운스트림 성능 또한 더 우수함을 나타낸다.
1 서론(Introduction)
Transformer(Vaswani et al., 2017)는 심층학습(deep learning) 분야에 혁신을 가져왔으며, 자연어 처리(Radford et al., 2019), 컴퓨터 비전(Dosovitskiy et al., 2021), 그 외 다양한 영역(Dong et al., 2018; Arnab et al., 2021)에서 전례 없는 발전을 이끌어냈다. 주의(attention) 메커니즘을 핵심으로 하는 Transformer는 데이터 내 복잡한 관계를 포착하는 데 탁월하여 현대 기계학습 응용에서 필수적인 도구가 되었다. 그러나 이러한 폭넓은 성공에도 불구하고, 특히 활성화 함수(activation function)의 선택과 관련하여 여전히 개선의 여지가 존재한다. 활성화 함수는 신경망 내 각 뉴런의 출력을 결정하는 데 중요한 역할을 한다. 전통적으로는 ReLU(Rectified Linear Unit, Nair & Hinton, 2010)와 그 변형들(Hendrycks & Gimpel, 2016; So et al., 2021)이 계산 효율성과 구현의 용이성 덕분에 널리 사용되어 왔다. 이러한 활성화 함수들은 효과적이긴 하지만, 데이터 내 복잡한 고차(high-order) 관계를 모델링하는 데 본질적인 한계를 가진다. 특히 Transformer 아키텍처에서는 미묘하고 복잡한 의존성을 포착하는 능력이 필수적이기 때문에, 이러한 한계는 성능을 제한하는 요인이 될 수 있다.
본 논문에서는 Transformer 아키텍처의 성능을 향상시키기 위해 특별히 설계된 새로운 범주의 다항식 조합 활성화 함수(Polynomial Composition Activation Functions, PolyCom)를 소개한다. 기존의 활성화 함수들이 주로 선형적(linear) 또는 구간별 선형(piecewise linear) 함수인 것과 달리, PolyCom은 데이터 내 보다 복잡한 패턴을 모델링할 수 있도록 한다. 이러한 활성화 함수의 표현력 증가는 모델의 표현 능력(expressive capacity)을 한층 강화하여, 기존 방식으로는 간과될 수 있는 고차(high-order) 상호작용을 포착할 수 있게 한다. 또한 기존의 다항식(Hornik et al., 1989; Trefethen, 2019)들이 겪는 불충분한 근사 능력, 값의 폭발(exploding values), 진동적 거동(oscillatory behavior)과 같은 문제와 달리, PolyCom은 ReLU 및 전통적인 다항식보다 훨씬 강력한 표현 능력을 가지며, Sobolev 공간(Sobolev space) 내에서 최적 근사(optimal approximation)를 달성함을 보인다.
우리는 Transformer 모델에 다항식 조합 활성화 함수(polynomial composition activations)를 통합함으로써, 복잡한 데이터 해석을 요구하는 과제에서 성능 향상을 이끌어낼 수 있다고 주장한다. 이 가설을 검증하기 위해, 우리는 밀집(dense) 및 희소(sparse) 아키텍처를 모두 포함한 대규모 언어 모델(large language models, LLMs)의 사전학습(pre-training) 구성에서 포괄적인 실험을 수행하였다. 이 평가에서는 다양한 벤치마크를 활용하여, 다항식 조합 활성화를 적용한 Transformer와 기존 활성화 함수를 사용하는 Transformer의 성능을 비교하였다. 그 결과, 제안된 방법은 모델의 정확도를 향상시킬 뿐만 아니라 수렴 속도(convergence rate)도 가속화함을 확인하였다. 이는 다항식 조합 활성화 함수가 딥러닝 응용에서 실질적인 이점을 제공함을 시사한다.
이 논문의 주요 기여(contributions)는 다음과 같이 요약된다.
- 우리는 다항식(polynomial)과 다른 유형의 함수를 조합(composition)하여 만든 새로운 활성화 함수 PolyCom을 제안한다. 특히, PolyCom의 두 가지 구체적 예시인 PolyReLU와 PolyNorm을 소개하고, 이를 Transformer 아키텍처에 통합하는 방법을 상세히 설명한다.
- 이론적으로, PolyReLU 네트워크가 ReLU 네트워크를 근사(approximate)하는 데 필요한 학습 가능한 파라미터 개수에 대한 경계를 유도하고, 그 반대 경우도 제시한다. 추가로, 크기가 O(ϵ^(-d/n))인 PolyReLU 네트워크가 Sobolev 공간(Sobolev spaces) 내 임의의 함수를 오차 허용치 ϵ 내에서 근사할 수 있으며, 이때 최적 근사율(optimal approximation rates)을 달성함을 보인다.
- 실험적으로는, 10억(1B) 파라미터 규모의 밀집(dense) 모델과 10억 활성(1B active)·70억 총합(7B total) 파라미터 규모의 MoE(Mixture of Experts) 모델을 대상으로 새로운 활성화 함수의 효과성을 검증하였다. 두 모델 모두에서 PolyCom은 수렴 속도를 가속화할 뿐 아니라, SwiGLU, GELU, ReLU 등의 기존 활성화 함수들을 현저히 능가하는 성능을 보였다.
논문의 구성은 다음과 같다. 2장에서는 PolyCom의 수학적 정식화와 Transformer 아키텍처 내 통합 방안을 제시한다. 3장에서는 PolyCom의 향상된 표현력과 효율성을 강조하는 포괄적 이론 분석을 제공한다. 4장에서는 대규모 언어모델(LLMs)을 대상으로 한 실험 결과를 상세히 설명한다. 5장에서는 활성화 함수 및 Transformer 모델 내 적용과 관련된 선행 연구를 개괄한다. 마지막으로 결론(Conclusion)에서는 본 논문을 정리하고 향후 연구 방향을 제시한다.
2 다항식 조합 활성화 함수 (Polynomial Composition Activation Function)
이 장에서는 다항식 조합 활성화 함수(PolyCom)의 수학적 정식화와 Transformer 아키텍처에 통합되는 방법을 제시한다.
PolyCom. 다항식 활성화 함수(polynomial activation function)에 대한 연구는 Hornik et al. (1989)의 기초적 연구로 거슬러 올라간다. 해당 연구에서는 다항식 활성화를 사용하는 신경망은 연속 함수 공간 내에서 조밀(dense)하지 않음을 보였다. 또한, 실증적 증거에 따르면 순수한 다항식 활성화를 사용하는 심층 신경망은 성능이 저조한 경향을 보인다(Trefethen, 2019). 이러한 한계를 극복하기 위해 우리는 다항식과 다른 함수를 조합한 새로운 형태의 PolyCom을 제안한다. 구체적으로는 두 가지 조합 방식을 탐구한다.
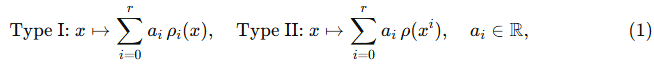
여기서 r∈N은 PolyCom의 차수(order)를 나타내며, ρ는 ReLU, PReLU, Sigmoid, SiLU, 정규화(normalization) 등 임의의 함수가 될 수 있다.
두 방식의 핵심적인 차이는 함수를 거친 뒤 거듭제곱(power)을 적용하는지, 아니면 거듭제곱을 적용한 뒤 함수를 적용하는지에 있다. 그러나 ρ가 비선형 함수일 경우, 이론적으로 두 방식은 동등한 표현력을 가진다. 이는 다항식 항이 조합(composition)에 대해 대칭적이므로 Type I과 Type II 모두 유사한 함수 계열을 근사할 수 있기 때문이다. 즉, ρ와 다항식 거듭제곱의 순서를 바꾸어도 복잡한 비선형 함수를 근사하는 능력은 변하지 않는다.
실험적으로는 학습 가능한 계수 a_i를 포함한 3차( r=3 ) PolyCom을 사용한다. 초기화 시에는 i=1,2,…,r에 대해 a_i = 1/r로 설정하고, a_0 = 0으로 둔다.
Type I PolyCom의 경우, 단순성 때문에 ReLU 함수와의 조합을 구체적으로 고려하며, 이를 PolyReLU라 부른다. 차수 r의 PolyReLU는 다음과 같이 정의된다.
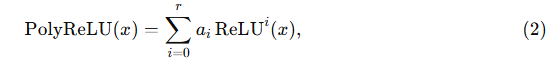
여기서

이다. 이 공식은 ReLU와 Square ReLU 모두를 확장한 형태로 볼 수 있다.
Type II PolyCom의 경우, 각 항의 크기가 일관되도록 거듭제곱을 정규화(normalize)하는 PolyNorm을 제안한다.


그림 2 설명
ReLU/GELU, SwiGLU, PolyReLU, PolyNorm을 사용하는 Transformer MLP 블록의 블록 다이어그램.
- “FC”는 완전연결층(Fully Connected layer)을 의미한다.
- “x^i”는 입력 텐서 의 i차 거듭제곱을 나타낸다.
- “a_j”는 학습 가능한 가중치 벡터 a의 -번째 원소를 나타낸다.
- “N”은 정규화(normalization) 연산을 의미한다.
Transformer에의 통합 (Integration into Transformer).
Transformer 아키텍처(Vaswani et al., 2017)는 멀티헤드 어텐션(Multi-Head Attention, MHA)과 위치별 피드포워드 네트워크(position-wise Feed-Forward Networks, FNN)라는 두 가지 모듈이 교대로 쌓여 구성된다. 이 중 활성화 함수(activation function)는 주로 FNN 층의 성능에 큰 영향을 미친다.
우리는 먼저 일반적인 FNN의 구조를 다음과 같이 정식화한다.

여기서 ρ는 ReLU, GeLU, PolyReLU, PolyNorm과 같은 활성화 함수를 나타낸다.
본 연구에서는 기존의 활성화 함수를 제안하는 PolyCom 계열 함수(PolyReLU, PolyNorm 등)로 대체하여 모델의 용량(capacity)과 성능을 향상시키며, 이는 그림 2에 시각적으로 설명되어 있다.
3 이론적 분석 (Theoretical Analysis)
2장에서 논의했듯이, PolyReLU와 PolyNorm은 동등한 표현력(expressivity)을 가진다. 분석을 단순화하기 위해, 본 장에서는 PolyReLU의 이론적 특성, 특히 그 표현력과 효과성에만 초점을 맞춘다. 추가적으로, GeLU와 SwiGLU와 같은 비선형 활성화 함수들은 원점 주변에서 테일러 다항식(Taylor polynomial)으로 국소적으로 근사될 수 있으므로, 우리는 주로 PolyReLU를 ReLU 및 다항식 활성화 함수와 비교한다. 혼동을 피하기 위해, ReLU 활성화를 사용하는 네트워크는 ReLU 네트워크, PolyReLU 활성화를 사용하는 네트워크는 PolyReLU 네트워크라고 부른다.
3.1 PolyReLU에 의한 ReLU 네트워크 근사 (Approximating ReLU Networks by PolyReLU)
이 절에서는 PolyReLU 네트워크가 ReLU 네트워크를 근사(approximate)하는 데 관한 이론적 결과를 제시한다. 다음의 보조정리(lemma)는 ReLU, ReLU², 그리고 다항식 활성화(polynomial activation)가 모두 PolyReLU 활성화의 특수한 경우임을 보여주며, 이를 통해 PolyReLU가 더 우수한 표현력을 지님을 강조한다. 이는 PolyReLU가 ReLU 및 다른 다항식 활성화 함수들에 비해 더 적은 학습 가능한 파라미터(trainable parameters)로도 더 강력한 근사 능력(approximation ability)을 가진다는 것을 의미한다.


3.2 PolyReLU를 ReLU 네트워크로 근사하기 (Approximating PolyReLU with ReLU networks)
이 절에서는 PolyReLU 네트워크를 ReLU 네트워크로 근사하는 데 관한 이론적 결과를 제시한다. 다음의 Lemma 2는 PolyReLU 활성화 함수가 주어진 오차 허용 범위(error tolerance) 내에서 ReLU 네트워크로 근사될 수 있음을 보여준다.



3.3 일반적인 매끄러운 함수의 근사 (Approximation of General Smooth Function)
Yarotsky (2017), Boullé et al. (2020)와 유사하게, 본 절에서는 Sobolev 공간(Adams & Fournier, 2003)의 맥락에서 PolyReLU 네트워크의 보편 근사 능력(universal approximation capabilities)을 탐구한다. 구체적으로, 우리는 PolyReLU 네트워크가 이 공간에서 최적 근사율(optimal approximation rate)을 달성함을 보인다. 이는 곧 PolyReLU 네트워크가 Sobolev 공간에서 일반적인 매끄러운 함수(smooth functions)를 근사하기 위해 다른 활성화 함수를 사용하는 네트워크보다 더 적은 파라미터만 필요하다는 것을 의미한다.





4 실험 (Experiments)
이 장에서는 대규모 언어 모델(LLMs)을 대상으로 한 실험을 통해 Transformer 내에서 PolyCom의 표현력(expressivity)과 효과성(effectiveness)을 입증한다.
4.1 실험 설정 (Setup)
Baseline.
우리는 두 가지 계열의 모델에서 PolyCom을 평가한다:
- 10억(1B) 규모의 dense 모델
- Mixture of Experts (MoE) 모델 – 활성(active) 파라미터 10억(1B), 전체(total) 파라미터 70억(7B).
- 1B dense 모델은 약 13억(1.3B)개의 파라미터를 가지며, 아키텍처는 Llama 2 (Touvron et al., 2023)와 유사하다.
- MoE 모델은 OLMoE 프레임워크(Muennighoff et al., 2024)를 사용하며, 총 69억(6.9B)개의 파라미터 중 13억(1.3B)개 파라미터만 활성화된다.
- 두 모델 모두 처음부터 학습(from scratch) 하였다.
비교 대상으로는 ReLU, Square ReLU, GELU, SwiGLU 등 여러 활성화 함수를 선정하여 PolyCom과 성능을 비교하였다.
모든 실험은 Nvidia A100-80G GPU에서 수행되었으며, Dense 모델은 GPU 32개, MoE 모델은 GPU 64개를 사용하였다.
내 기억이 맞다면 polynorm 비슷한것들은 2019년도 이후에도 많았던것 같다. 특히 다항식은 RL쪽에서 쓰인 기억이있는데 논문이 기억이 안난다. 그 때도 좋다고는 했는데 안쓰였던거로 기억난다.
1. 다항식 계열 활성화의 연구 흐름
- 1990년대–2000년대 초반: Universal Approximation 정리(Universal Approximation Theorem)를 논할 때 “다항식 활성화”가 한 번 부각됨 (Hornik 등).
- 2017~2019년: ReLU가 표준이 된 이후, “ReLU²”, “PolyNet”, “Pade Activation Units(PAU, 2019)” 같은 다항식·유리함수 근사 기반 활성화 함수가 등장.
- 2019 이후: Rational/Polynomial 계열 활성화가 여러 분야에 시도되었음. 특히 RL에서는 비선형성 표현을 강화하려고 논문들이 실험했는데,
- Rational Activation Functions (RAU, 2019~2020)
- Polynomial Approximations of Value Functions in RL
같은 연구에서 등장했어요.
2. RL 쪽에서의 사례
- Value Function 근사에서 다항식 기저(polynomial basis)나 Chebyshev polynomial을 사용 → 이건 사실 “정책 평가(policy evaluation)” 쪽에서 안정성을 위한 전통적 접근.
- Activation으로 polynomial류를 쓰자는 제안도 있었지만,
- 고차수 다항식일수록 값 폭발(exploding values), 진동(oscillation) 문제가 컸고
- BatchNorm, LayerNorm 같은 정규화 기법과 충돌하는 경우도 있었음.
그래서 초반에는 “표현력 좋다”라는 평가를 받았지만, 안정성 문제 + GPU 최적화가 ReLU 계열에 집중되다 보니 산업/대규모 모델에서는 채택되지 못했습니다.
3. 최근 다시 부각되는 이유 (PolyNorm, PolyCom 같은 흐름)
- 지금 PolyNorm/PolyCom이 새롭게 주목받는 이유는,
- Transformer 아키텍처에서는 고차 상호작용(higher-order interactions) 학습이 중요하고,
- normalization 기법과 조합해서 다항식 항을 안정적으로 다룰 수 있게 되었기 때문.
- 즉, 예전에는 "좋지만 unstable" → 지금은 **"안정화된 형태로 다시 등장"**이라고 보는 게 맞습니다.



평가(Evaluation).
PolyCom을 적용한 LLM의 성능을 평가하기 위해 다음과 같은 다양한 공개 벤치마크를 사용한다:
- ARC-Easy, ARC-Challenge (Clark et al., 2018)
- HellaSwag (Zellers et al., 2019)
- PIQA (Bisk et al., 2020)
- SciQ (Welbl et al., 2017)
- CoQA (Reddy et al., 2019)
- Winogrande (Sakaguchi et al., 2021)
- MMLU (Hendrycks et al., 2021)
- BoolQ (Clark et al., 2019)
- COPA (Gordon et al., 2012)
- CSQA (Talmor et al., 2019)
- OBQA (Mihaylov et al., 2018)
- SocialIQA (Sap et al., 2019)
성능 측정에는 LM Eval Harness (Gao et al., 2023)를 사용하여 표준화된 평가를 수행하였다.
4.2 Dense 모델 결과 (Results on Dense Model)
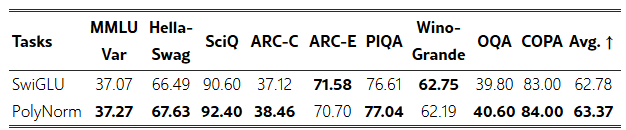
표 1: 10억(1B) 규모의 Dense 모델에서 서로 다른 활성화 함수를 적용했을 때의 결과를 요약하였다. 평가 지표는 훈련 손실(training loss), 검증 퍼플렉서티(validation perplexity), 그리고 다운스트림 정확도(downstream accuracy, %)이다. ARC-E와 ARC-C는 각각 ARC-Easy와 ARC-Challenge를 의미한다. 각 열에서 가장 우수한 결과는 굵게 표시하였다. "Avg."는 모든 다운스트림 과제에서의 평균 정확도를 나타낸다.

1B Dense 모델의 학습 동역학 (Training Dynamics).
그림 1은 1B Dense 모델에서 서로 다른 활성화 함수를 사용했을 때의 학습 동역학을 비교한 것이다. 그림에서 볼 수 있듯이, PolyReLU와 PolyNorm을 사용하는 모델은 학습 전 과정에서 다른 활성화 함수를 사용하는 모델들보다 훈련 손실과 검증 퍼플렉서티가 낮게 유지된다. 이는 PolyCom이 LLM의 수렴 속도를 가속화함을 의미한다. 또한 PolyReLU와 PolyNorm을 적용한 모델은 다운스트림 과제에서도 꾸준히 큰 폭으로 다른 모델들을 능가하여, LLM의 전반적인 표현력(expressivity)과 효과성(effectiveness)을 개선하는 데 있어 PolyCom의 장점을 보여준다.
다운스트림 평가 (Downstream Evaluation).
표 1은 2,500억(250B) 개의 훈련 토큰을 처리한 이후의 훈련 손실, 검증 퍼플렉서티, 그리고 다운스트림 과제 정확도(%)를 제시한다. 다운스트림 과제에는 ARC-Easy, ARC-Challenge, HellaSwag, PIQA, SciQ, Winogrande가 포함된다. 보다 상세한 결과는 부록 D(Appendix D)에 제공된다. 실험 결과는 PolyCom 계열(PolyReLU, PolyNorm)이 다른 활성화 함수들을 능가함을 명확히 보여준다. 예를 들어, PolyNorm은 여섯 개의 다운스트림 과제에서 SwiGLU보다 평균 1.21% 더 높은 정확도를 기록하였다. 이는 Transformer 모델에서 활성화 함수로서 PolyCom의 표현력과 효율성을 강하게 뒷받침한다.
4.3 MoE 모델 결과 (Results on MoE Model)
우리의 MoE 모델 실험은 OLMoE-1B-7B를 기반으로 하며, 이는 활성 파라미터 10억(1B), 전체 파라미터 70억(7B)을 가진다 (Muennighoff et al., 2024). 계산 자원의 제약으로 인해, 우리는 Dense 모델에서 가장 우수한 성능을 보인 PolyNorm 활성화 함수와, 현재 LLM 아키텍처에서 널리 사용되는 SwiGLU 활성화 함수만 비교하였다.

그림 3: 2000억(200B) 학습 토큰으로 학습된 MoE 모델의 C4 및 Wikipedia 학습/검증 손실. SwiGLU와 PolyNorm을 비교하였으며, PolyNorm은 더 낮은 학습 및 검증 손실을 보여 더 빠른 수렴을 나타낸다.

그림 4: 동일한 2000억 토큰으로 학습된 MoE 모델의 다운스트림 성능 (HellaSwag, MMLU Var, ARC-Challenge, SciQ). PolyNorm을 사용한 모델은 SwiGLU 대비 모든 과제에서 크게 우수한 성능을 보이며, 뛰어난 일반화 성능을 입증한다.
MoE 모델의 학습 동역학 (Training dynamics).
그림 3은 2000억 토큰으로 학습된 MoE 모델의 훈련 및 검증 손실을 보여준다. PolyNorm을 사용한 모델은 SwiGLU에 비해 일관되게 낮은 손실을 기록하며, 이는 PolyNorm이 더 빠른 학습을 가능하게 한다는 것을 의미한다.
그림 4는 HellaSwag, MMLU Var3^, ARC-Challenge, SciQ에서의 다운스트림 성능을 나타낸다. PolyNorm은 모든 과제에서 SwiGLU를 능가하며, 두드러진 성능 향상을 보여준다. 이는 PolyNorm의 우수한 일반화 능력을 뒷받침한다.
3^ MMLU Var는 MMLU (Hendrycks et al., 2021)의 변형으로, 다양한 few-shot 설정을 적용한 벤치마크 (Muennighoff et al., 2024).
표 2: 서로 다른 활성화 함수를 사용한 MoE 모델의 검증 손실. CC는 Common Crawl을 의미한다. 각 열의 최고 성능은 굵게 표시하였다.

다운스트림 평가 (Downstream Evaluation).
표 2는 11개 데이터셋에서의 검증 손실을 제시한다. PolyNorm은 모든 데이터셋에서 SwiGLU보다 일관되게 더 낮은 검증 손실을 기록하며, 평균적으로 0.02의 개선을 보였다. 또한 표 3에서는 PolyNorm이 8개의 다운스트림 과제에서 SwiGLU보다 더 나은 성능을 기록함을 확인하였다. 이 결과는 PolyNorm 활성화 함수를 적용한 모델이 우월한 성능을 발휘함을 보여준다. 추가적인 결과는 부록 E(Appendix E)에 제시되어 있다.
표 3: 서로 다른 활성화 함수를 사용한 MoE 모델의 다운스트림 평가 결과. ARC-C, ARC-E, OQA는 각각 ARC-Challenge, ARC-Easy, OpenbookQA를 의미한다. 각 열의 최고 성능은 굵게 표시하였다.
4.4 Ablations and Analysis
PolyCom의 차수(Order of PolyCom).
먼저 PolyCom의 차수(order)가 성능에 미치는 영향을 조사하였다. 우리는 PolyReLU의 차수 r∈{2,3,4}로 변경하며 결과를 그림 5(a)에 제시하였다. 그림에서 볼 수 있듯이, 차수가 증가할수록 수렴 속도가 개선된다. 그러나 차수 3과 4 사이에는 수렴 속도에서 눈에 띄는 차이가 없다. 또한 차수를 높이면 계산 오버헤드와 overflow 문제가 발생할 수 있는데, 특히 저정밀도 연산(low-precision arithmetic)을 사용할 때 이러한 현상이 두드러진다. 이러한 관찰에 기반해, 우리는 성능과 계산 효율성 사이의 균형을 고려하여 실험에서 기본 차수(default order)로 r=3을 선택하였다.
다양한 다항식 조합 함수(Different Polynomial Composition Functions).
PolyReLU, PolyPReLU, PolyNorm, PolyReLUNorm을 비교하여 다양한 다항식 조합 함수의 효과를 평가하였으며, 그 결과는 그림 5(b)에 제시하였다. 실험 결과, 정규화(normalization)를 조합 함수로 사용하는 PolyNorm이 가장 낮은 학습 손실과 최고의 전반적 성능을 달성하였다. 이는 정규화가 학습을 안정화하고 모델의 일반화 능력을 향상시키는 데 중요한 역할을 함을 시사한다. 반면, ReLU와 정규화를 결합한 PolyReLUNorm은 중간 수준의 성능을 보여주었으며, 이는 더 복잡한 조합이 항상 더 나은 결과로 이어지지는 않음을 시사한다.
ReLU의 변형(Variants of ReLU).
그림 5(c)에서는 ReLU와 ReLU²를 포함한 다양한 ReLU 계열 활성화 함수를 비교하였다. PolyReLU는 모든 과제에서 ReLU와 ReLU²보다 일관되게 더 우수한 성능을 보였으며, 이는 다항식 조합(polynomial composition)의 장점을 강조한다. 이러한 결과는 PolyCom을 통해 고차항(higher-order terms)을 도입하면 모델이 더 복잡한 데이터 상호작용을 포착할 수 있어, 모델 크기나 복잡도를 크게 늘리지 않고도 활성화 함수의 표현력을 향상시킬 수 있다는 가설을 강화한다.
가중치의 랭크(Rank of Weights).
PolyCom이 모델 성능을 어떻게 향상시키는지를 이해하기 위해, Transformer의 각 FNN 층에서 가중치의 랭크(rank)를 분석하였다. 여기서 가중치의 유효 차원성을 측정하기 위해 effective rank(Roy & Vetterli, 2007)를 사용하였으며, 그 정의는 부록 C.2에 제시되어 있다. 그림 6은 PolyReLU와 PolyNorm이 SwiGLU, GELU, ReLU와 같은 다른 활성화 함수들에 비해 더 높은 가중치 랭크를 만들어냄을 보여준다. 가중치 행렬의 랭크가 높다는 것은 데이터 내 복잡한 패턴을 표현할 수 있는 더 큰 용량(capacity)을 의미한다. 이러한 결과는 PolyCom이 FNN 층이 보유한 파라미터를 더 잘 활용하도록 하여 Transformer의 표현력을 높이고, 궁극적으로 다운스트림 과제에서 더 나은 일반화 성능을 이끌어냄을 시사한다.
계층 간 유사도(Layer-wise Similarity).
우리는 또한 코사인 유사도(cosine similarity)를 활용해 은닉 상태(hidden states)의 계층 간 유사도를 분석하였으며, 그 결과는 그림 7에 제시되어 있다. Dense 모델과 MoE 모델 모두에서 SwiGLU와 PolyNorm을 비교하였다. 결과는 PolyNorm이 SwiGLU에 비해 일관되게 더 낮은 계층 간 유사도를 유지함을 보여준다. 이는 PolyNorm이 계층 간 더 큰 다양성(diversity)을 촉진한다는 것을 의미한다. 이러한 다양성은 깊은 층들이 단순히 이전 층의 기능을 복제하지 않고, 더 복잡한 표현을 학습할 수 있게 해준다. 특히, 깊은 층에서 PolyNorm과 SwiGLU 간 코사인 유사도의 격차가 더 크게 벌어지는데, 깊은 층은 일반적으로 다운스트림 과제 성능에 더 중요한 역할을 한다. 따라서 계층 전반에 걸친 다양성 증가는 모델이 복잡한 관계를 포착할 수 있는 능력을 향상시켜, 결과적으로 LLM의 전반적인 효과성을 개선한다.
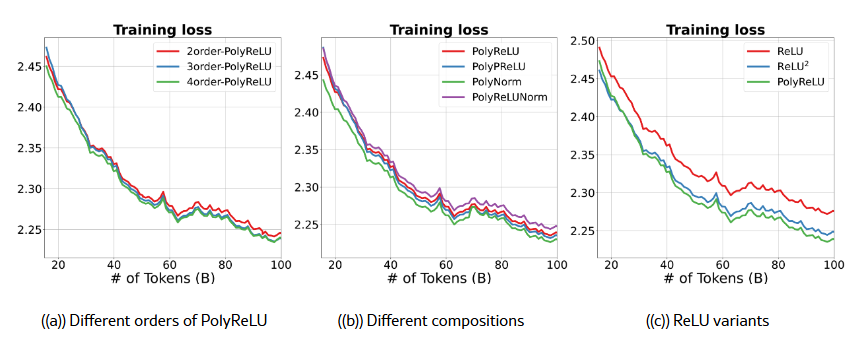
그림 5: 서로 다른 활성화 함수를 사용한 10억(1B) Dense 모델의 학습 손실.
- 5(a): PolyReLU의 차수(order) 비교.
- 5(b): 서로 다른 조합 함수를 사용한 PolyCom 비교.
- 5(c): ReLU 활성화 함수의 다양한 변형 비교.

그림 6: 각 FNN 층에서의 가중치 랭크(rank).
- 6(a), 6(b): Dense 모델.
- 6(c), 6(d): MoE 모델.

그림 7: 은닉 상태(hidden states)의 계층별 코사인 유사도(layer-wise cosine similarity).
- 7(a), 7(b): SwiGLU와 PolyNorm을 적용한 1B Dense 모델.
- 7(c), 7(d): SwiGLU와 PolyNorm을 적용한 MoE 모델.
5 관련 연구 (Related Work)
활성화 함수의 설계는 신경망 연구에서 매우 중요한 분야로, 딥러닝 모델의 성능과 능력에 직접적으로 영향을 미친다. 초기 활성화 함수인 Sigmoid와 Tanh는 부드러운 비선형 변환(smooth nonlinear transformation) 덕분에 널리 사용되었다(Goodfellow et al., 2016). 그러나 이러한 함수들은 기울기 소실(vanishing gradients) 문제를 겪었고, 이로 인해 심층 신경망을 효과적으로 학습시키는 데 어려움이 있었다.
ReLU(Rectified Linear Unit) (Nair & Hinton, 2010)의 도입은 이러한 문제를 완화시켰다. ReLU는 단순하면서도 포화되지 않는(non-saturating) 비선형성을 제공하여, 이후 다양한 딥러닝 응용에서 표준으로 자리 잡았다. 또한, Leaky ReLU (Maas et al., 2013), Parametric ReLU (PReLU) (He et al., 2015)와 같은 ReLU의 변형은 입력이 음수일 때도 작은 비영(非零) 기울기를 허용함으로써 dying ReLU 문제를 해결하고자 했다. 이 외에도 Exponential Linear Unit (ELU) (Clevert, 2015)는 더 매끄러운 활성화 프로파일을 제공하여, 특정 과제에서 더 나은 일반화 성능과 빠른 수렴을 이끌었다. 한편, Manessi & Rozza (2018)는 가중치가 적용된 기본 활성화 함수들을 조합하여 성능 향상을 도모하기도 했다.
한편, 다항식 활성화 함수(polynomial activation functions) (Hornik et al., 1989; Oh et al., 2003)는 사용 빈도는 낮지만, 고차(high-order) 복잡한 관계를 더 효과적으로 모델링할 수 있는 능력 때문에 다양한 맥락에서 연구되어 왔다. 예를 들어, Lokhande et al. (2020)는 Hermite 다항식 활성화를 도입해 pseudo-label 정확도를 향상시켰고, Chrysos et al. (2020)는 이미지 및 오디오 처리와 같은 다양한 도메인에 적용 가능한 다항식 네트워크, Π-nets를 제안했다. 이어서 Chrysos et al. (2023)는 정규화 기법을 활용해 다항식 네트워크의 성능을 개선하였다. 이러한 연구들은 다항식 함수가 정교한 고차 상호작용을 포착함으로써 신경망의 표현력을 강화할 수 있는 잠재력을 강조한다.
또한 이론적 측면에서도, 다항식 함수의 표현력(expressivity)과 근사 능력(approximation power)은 엄밀하게 탐구되어 왔다(Kileel et al., 2019; Kidger & Lyons, 2020; Kubjas et al., 2024).
Transformer에서의 활성화 함수 선택 역시 중요한 연구 분야가 되었다. 원래 자연어 처리(NLP)를 위해 개발된 Transformer (Vaswani et al., 2017)는 이미지 인식, 음성 처리, 강화학습 등 다양한 과제에 효과적으로 적용되어 왔다. 그러나 그 광범위한 적용 가능성에도 불구하고, Transformer에서 주로 사용되는 활성화 함수는 ReLU와 GELU에 국한되어 있으며, 그 진화는 매우 제한적이었다.
최근 연구에서는 이러한 기존 활성화 함수들의 대안을 탐구하기 시작했다. 예를 들어, Swish 활성화 함수(Ramachandran et al., 2017; Shazeer, 2020)와 Mish 활성화 함수(Misra, 2019)는 매끄럽고 비단조적(non-monotonic)인 특성을 지니며, 모델 성능 및 학습 안정성 측면에서 잠재적 이점을 제공한다. 또한, Gated Linear Units (GLU)가 Dauphin et al. (2017)에 의해 제안되었고, 그 변형 중 하나인 SwiGLU(Shazeer, 2020)는 LLaMA 시리즈(Touvron et al., 2023)와 같은 모델에서 널리 사용되고 있다.
6 결론 (Conclusions)
본 논문에서는 Polynomial Composition Activation (PolyCom)을 제안하고, 이를 Transformer 모델 내에서 적용했을 때의 효과성을 입증하였다. PolyCom은 고차 상호작용(higher-order interactions)을 포착할 수 있도록 하여 모델의 정확도와 수렴 속도 모두를 향상시킨다.
다양한 대규모 언어 모델 아키텍처와 여러 벤치마크 데이터셋을 대상으로 수행한 실험에서, PolyCom은 기존의 활성화 함수들을 일관되게 능가하는 성능을 보여주었다. 추가적인 ablation 연구에서는 PolyCom이 가중치의 랭크를 높이고 계층 간 중복성을 줄임으로써 모델의 표현력을 향상시킨다는 사실이 드러났다.
이러한 결과는 다항식 기반 활성화 함수(polynomial-based activations)가 Transformer 모델을 개선할 수 있는 큰 잠재력을 지니고 있음을 강조하며, 향후 연구의 새로운 방향을 제시한다.
import torch
import torch.nn as nn
from typing import Literal, Optional
class RMSNorm(nn.Module):
"""간단한 RMSNorm. 배치 통계 없이 feature 차원만 사용."""
def __init__(self, dim: int, eps: float = 1e-6):
super().__init__()
self.weight = nn.Parameter(torch.ones(dim))
self.eps = eps
def forward(self, x: torch.Tensor) -> torch.Tensor:
# x: (..., dim)
norm = x.pow(2).mean(dim=-1, keepdim=True).add(self.eps).rsqrt()
return self.weight * x * norm
def build_norm(norm_type: Literal["none", "layernorm", "rmsnorm", "groupnorm"],
dim: int,
groups: int = 8) -> nn.Module:
if norm_type == "none":
return nn.Identity()
if norm_type == "layernorm":
return nn.LayerNorm(dim)
if norm_type == "rmsnorm":
return RMSNorm(dim)
if norm_type == "groupnorm":
# 토큰 피처를 채널로 보고 1D GroupNorm처럼 사용하려면 (B*T, C, 1) 형태가 필요
# 본 레이어에서는 token-wise 사용을 위해 LayerNorm이나 RMSNorm을 추천
raise NotImplementedError("이 예시에서는 groupnorm은 비권장")
raise ValueError(f"unknown norm_type: {norm_type}")
class PolyNorm(nn.Module):
"""
PolyNorm 레이어
- 입력: (B, T, D_in)
- 처리:
x1 = FC_in(x) → 각 차수 k=0..r에 대해 x1^k 계산 → 항별 Norm → 항별 스칼라 α_k 곱
→ concat(dim=-1) → FC_out
- 출력: (B, T, D_out)
주요 하이퍼파라미터
- degree: 다항식 최고차수 r (총 r+1개 분기)
- hidden_dim: 중간 채널 크기
- norm_type: "none" | "layernorm" | "rmsnorm"
- use_bias: FC 가중치 bias 사용 여부
- preact: 입력에 비선형을 줄지 여부 (예: ReLU). PolyNorm 원그림은 preact 없이 전개되어 있어 기본 False
"""
def __init__(
self,
d_in: int,
d_out: int,
hidden_dim: int,
degree: int = 3,
norm_type: Literal["none", "layernorm", "rmsnorm"] = "rmsnorm",
use_bias: bool = True,
preact: Optional[nn.Module] = None,
drop: float = 0.0,
):
super().__init__()
assert degree >= 0
self.degree = degree
self.preact = preact
self.fc_in = nn.Linear(d_in, hidden_dim, bias=use_bias)
# 항별 정규화 모듈과 스칼라 계수 α_k
self.branch_norms = nn.ModuleList([build_norm(norm_type, hidden_dim) for _ in range(degree + 1)])
self.branch_alpha = nn.Parameter(torch.ones(degree + 1))
# concat 뒤 투영
self.fc_out = nn.Linear(hidden_dim * (degree + 1), d_out, bias=use_bias)
self.dropout = nn.Dropout(drop)
# 작은 초기화로 안정화
nn.init.xavier_uniform_(self.fc_in.weight)
nn.init.xavier_uniform_(self.fc_out.weight)
if use_bias:
nn.init.zeros_(self.fc_in.bias)
nn.init.zeros_(self.fc_out.bias)
def forward(self, x: torch.Tensor) -> torch.Tensor:
"""
x: (B, T, D_in)
"""
h = self.fc_in(x) # (B, T, H)
if self.preact is not None:
h = self.preact(h)
# k=0..r 병렬 분기. x^0은 1이므로 ones로 대체
branches = []
for k in range(self.degree + 1):
if k == 0:
b = torch.ones_like(h)
elif k == 1:
b = h
else:
b = h.pow(k)
b = self.branch_norms[k](b)
b = self.branch_alpha[k] * b
branches.append(b)
# feature 차원 concat
h_cat = torch.cat(branches, dim=-1) # (B, T, H*(r+1))
out = self.fc_out(self.dropout(h_cat)) # (B, T, D_out)
return out
# 사용 예시 1: Transformer MLP를 PolyNorm으로 대체
class PolyNormFFN(nn.Module):
def __init__(self, d_model: int, expansion: int = 4, degree: int = 3, drop: float = 0.1):
super().__init__()
hidden = d_model * expansion
self.core = PolyNorm(
d_in=d_model,
d_out=d_model,
hidden_dim=hidden,
degree=degree,
norm_type="rmsnorm", # 배치 통계 비의존
preact=None, # 도식에 맞춰 비활성
drop=drop,
)
def forward(self, x):
# x: (B, T, D)
return self.core(x)
# 사용 예시 2: 간단한 확인
if __name__ == "__main__":
B, T, D = 2, 16, 64
x = torch.randn(B, T, D)
ffn = PolyNormFFN(d_model=D, expansion=4, degree=3, drop=0.1)
y = ffn(x)
print(x.shape, "->", y.shape) # torch.Size([2, 16, 64]) -> torch.Size([2, 16, 64])'인공지능' 카테고리의 다른 글
| Less is More: Recursive Reasoning with Tiny Networks (2) | 2025.10.09 |
|---|---|
| Vision-Zero: Scalable VLM Self-Improvement via Strategic Gamified Self-Play (2) | 2025.10.06 |
| DINOv3 (2) | 2025.08.19 |
| Nano Banana (4) | 2025.08.17 |
| YOLOE: Real-Time Seeing Anything (6) | 2025.08.07 |

