https://arxiv.org/abs/2510.04871?ref=refetch.io
Less is More: Recursive Reasoning with Tiny Networks
Hierarchical Reasoning Model (HRM) is a novel approach using two small neural networks recursing at different frequencies. This biologically inspired method beats Large Language models (LLMs) on hard puzzle tasks such as Sudoku, Maze, and ARC-AGI while tra
arxiv.org
초록(Abstract)
Hierarchical Reasoning Model (HRM)은 서로 다른 주기로 반복(recursing)하는 두 개의 작은 신경망을 사용하는 새로운 접근 방식이다. 생물학적 영감을 받은 이 방법은 Sudoku, Maze, ARC-AGI와 같은 난이도 높은 퍼즐 과제에서 대규모 언어 모델(LLM)을 능가하며, 단 약 1,000개의 예시와 2,700만 개의 파라미터를 가진 작은 모델로 학습되었다. HRM은 작은 네트워크로 어려운 문제를 해결할 수 있는 잠재력을 지니지만, 아직 충분히 이해되지 않았고 최적화되지 않았을 가능성도 있다. 이에 우리는 훨씬 단순한 재귀적(reasoning) 추론 접근법인 Tiny Recursive Model (TRM)을 제안한다. TRM은 단 2개의 층(layer)을 가진 하나의 초소형 네트워크만을 사용하면서도 HRM보다 훨씬 높은 일반화 성능(generalization)을 달성한다. 700만 개의 파라미터만으로 TRM은 ARC-AGI-1에서 45%, ARC-AGI-2에서 8%의 테스트 정확도를 기록하며, 이는 DeepSeek R1, o3-mini, Gemini 2.5 Pro와 같은 대부분의 LLM보다 높은 수치이다. 그럼에도 TRM은 이들 모델의 0.01% 미만의 파라미터만을 사용한다.
키워드: reasoning, recurrent, ARC-AGI
1. 서론(Introduction)
강력한 성능을 지닌 대규모 언어 모델(Large Language Models, LLMs)조차도 어려운 질문-답변형 문제(hard question-answer problems)에서는 종종 어려움을 겪는다. 이유는 간단하다 — LLM은 자가회귀(auto-regressive) 방식으로 출력을 생성하기 때문에, 단 하나의 잘못된 토큰(token)이 전체 답변을 무효화할 위험이 매우 크다.
이러한 신뢰성 문제를 개선하기 위해 LLM들은 주로 사고의 연쇄(Chain-of-Thought, CoT) (Wei et al., 2022)와 시험 시 계산(Test-Time Compute, TTC) (Snell et al., 2024)에 의존한다. CoT는 인간의 추론 과정을 모방하려는 시도로, 모델이 최종 답변을 내기 전에 단계별(step-by-step) 추론 과정을 샘플링하도록 유도한다. 이 방식은 정확도를 향상시킬 수 있으나, 비용이 크고, 고품질의 추론 데이터(이는 항상 존재하지 않는다)가 필요하며, 생성된 추론 과정이 잘못될 경우 불안정(brittle)하다는 한계가 있다.
이 신뢰성을 더 높이기 위해, 시험 시 계산(TTC)은 K개의 출력 중 가장 빈도가 높은 답변이나 보상이 가장 높은 답변을 선택하는 방법(Snell et al., 2024)을 사용하기도 한다.
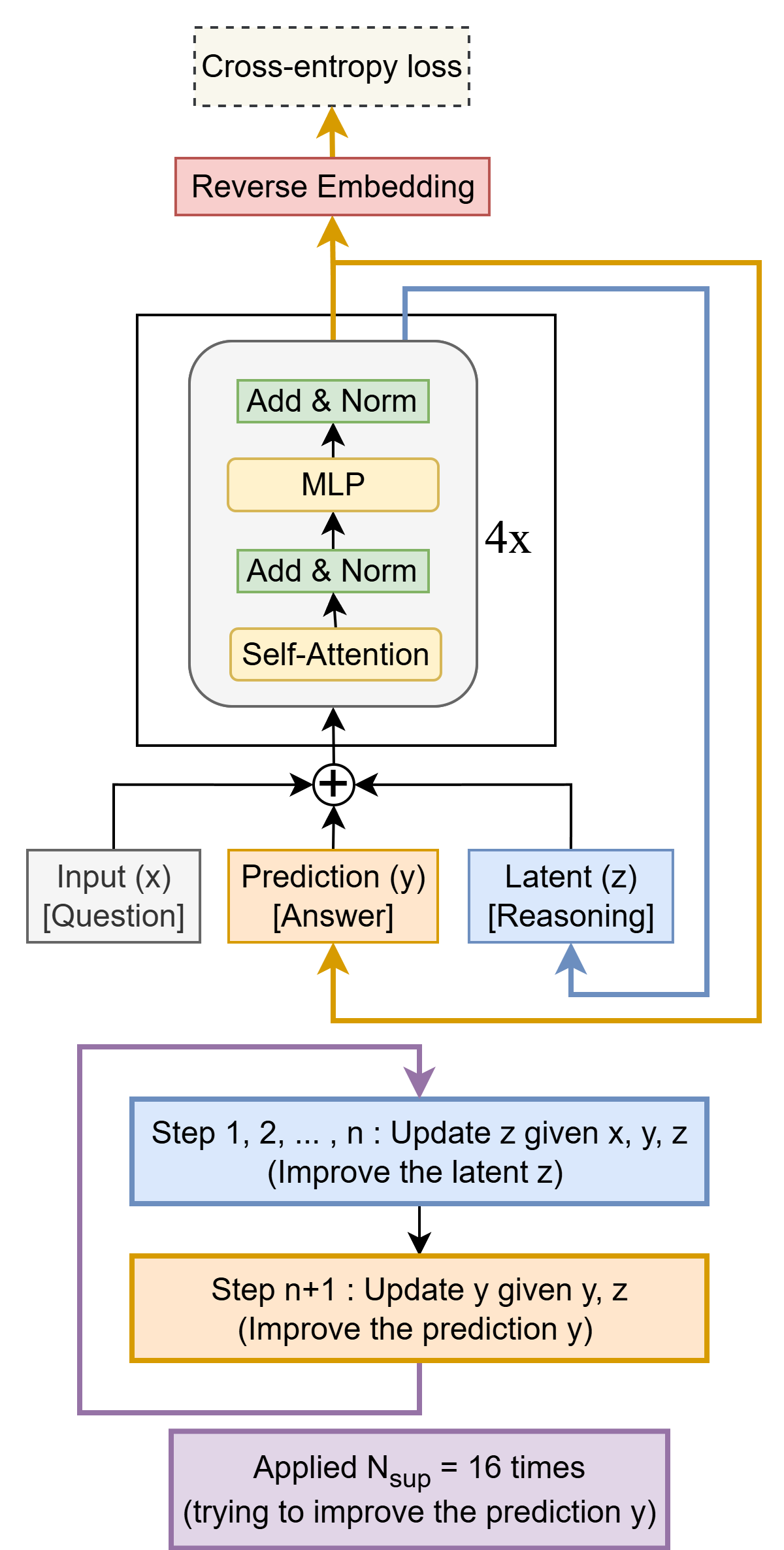
그림 1: Tiny Recursive Model (TRM)은 작은 네트워크를 사용하여 예측된 답변 y를 재귀적으로(recursively) 개선하는 모델이다. 이 모델은 임베딩된 입력 질문 x, 초기 임베딩된 답변 y, 그리고 잠재 벡터(latent) z로부터 시작한다. 최대 N_sup = 16번의 개선 단계(improvement steps)에 걸쳐, TRM은 자신의 답변 y를 점진적으로 향상시키려 시도한다. 그 과정은 다음 두 단계로 이루어진다.
i) 질문 x, 현재 답변 y, 현재 잠재 벡터 z를 바탕으로 잠재 벡터 z를 n번 재귀적으로 갱신한다 (재귀적 추론, recursive reasoning).
ii) 이후, 현재 답변 y와 잠재 벡터 z를 기반으로 답변 y를 갱신한다.
이러한 재귀적 절차를 통해 모델은 이전 답변의 오류를 점진적으로 수정하며, 매우 효율적인 파라미터 사용(parameter-efficient)으로 과적합(overfitting)을 최소화하면서 답변의 품질을 꾸준히 개선할 수 있다.
하지만 이것만으로는 충분하지 않다. Chain-of-Thought(CoT)와 Test-Time Compute(TTC)를 사용하는 LLM이라도 모든 문제를 해결할 수 있는 것은 아니다. LLM은 2019년 이후 ARC-AGI(Chollet, 2019) 과제에서 상당한 발전을 이루었지만, 여전히 인간 수준의 정확도(human-level accuracy)에는 도달하지 못했다(이 논문 작성 시점 기준으로 6년이 지난 현재까지도). 더 나아가, ARC-AGI-2와 같은 최신 버전에서는 성능이 더욱 저조하다. 예를 들어 Gemini 2.5 Pro는 매우 높은 수준의 TTC를 적용하고도 테스트 정확도 4.9%에 그친다(Chollet et al., 2025; ARC Prize Foundation, 2025b).
이에 대한 대안적 접근 방향(alternative direction)으로 Wang et al.(2025)은 새로운 방법을 제시했다. 그들은 Hierarchical Reasoning Model (HRM)이라는 새로운 구조를 통해, LLM이 고전하던 퍼즐형 과제들(Sudoku, Maze, ARC-AGI 등)에서 높은 정확도를 달성했다. HRM은 지도학습(supervised learning) 기반 모델이며, 두 가지 핵심 혁신을 가지고 있다:
- 재귀적 계층 추론(recursive hierarchical reasoning)
- 깊은 감독(deep supervision)
재귀적 계층 추론(recursive hierarchical reasoning)은 두 개의 작은 네트워크를 반복적으로 호출하여 답을 예측하는 방식이다.
- 고주파(high frequency)로 작동하는 f_L,
- 저주파(low frequency)로 작동하는 f_H 두 네트워크가 존재하며, 각각은 서로 다른 잠재 표현(latent feature)을 생성한다. 즉, f_L은 z_H를 출력하고, f_H는 z_L을 출력한다. 이 두 특징(z_L, z_H)은 서로의 입력으로 다시 사용된다. 저자들은 인간의 뇌가 서로 다른 시간적 주파수(temporal frequency)에서 작동하며 감각 정보를 계층적으로 처리한다는 생물학적 근거를 들어, 이런 다단계 재귀 구조를 정당화하였다.
깊은 감독(Deep supervision)은 여러 단계의 감독(supervision step)을 통해 점진적으로 답변을 개선하는 방식이다. 이 과정에서 두 개의 잠재 특징(z_L, z_H)은 다음 단계의 초기값(initialization)으로 전달되지만, 계산 그래프(computational graph)로부터 분리(detach)되어 gradient가 역전파되지 않도록 한다. 이 구조는 잔차 연결(residual connections)을 만들어, 하나의 순전파(forward pass)에서 메모리 한계로 구현하기 어려운 매우 깊은 신경망의 효과를 모사한다.
한편, ARC-AGI 벤치마크에 대한 독립 분석 결과에 따르면, HRM의 성능 향상의 주요 요인은 재귀적 구조가 아니라 깊은 감독(deep supervision)이었다(ARC Prize Foundation, 2025a).
- 단일 단계 감독(single-step supervision)에서 정확도 19% → 39%로 2배 향상되었지만,
- 재귀적 계층 추론은 단일 순전파 모델 대비 35.7% → 39.0%로 소폭 향상에 그쳤다. 이 결과는 “여러 단계의 감독 간 reasoning은 유의미하지만, 각 단계 내부의 recursion 자체는 큰 영향을 주지 않는다”는 것을 시사한다.
이에 본 연구에서는 재귀적 추론(recursive reasoning)의 효과를 훨씬 더 극대화할 수 있음을 보인다. 우리는 Tiny Recursive Model (TRM)을 제안하는데, 이는 단 2개의 층(layer)으로 구성된 매우 작은 네트워크를 사용하면서도 HRM보다 훨씬 높은 일반화 성능(generalization)을 다양한 문제에서 달성한다. 그 결과, 우리는 다음과 같이 최신 최고 성능(state-of-the-art)을 크게 갱신하였다.
- Sudoku-Extreme: 55% → 87%
- Maze-Hard: 75% → 85%
- ARC-AGI-1: 40% → 45%
- ARC-AGI-2: 5% → 8%
2. 배경(Background)
HRM(Hierarchical Reasoning Model)의 구조는 Algorithm 2에 기술되어 있으며, 아래에서 그 세부 내용을 설명한다.
2.1 구조 및 목표 (Structure and Goal)
HRM의 중심은 지도 학습(supervised learning)이다. 즉, 주어진 입력(input)에 대해 적절한 출력을 생성하는 것이 목표이다.
입력과 출력은 모두 [B, L] 형태를 가진다고 가정한다. (만약 길이가 다를 경우, padding token을 추가하여 길이를 맞춘다.)
여기서
- B는 배치 크기(batch size),
- L은 컨텍스트 길이(context length)를 의미한다.
HRM의 학습 가능한 구성 요소 (Learnable Components)
HRM은 네 가지 학습 가능한 모듈로 구성된다.
- 입력 임베딩 (Input embedding): f_I(·; θ_I)
- 저수준 순환 네트워크 (Low-level recurrent network): f_L(·; θ_L)
- 고수준 순환 네트워크 (High-level recurrent network): f_H(·; θ_H)
- 출력 헤드 (Output head): f_O(·; θ_O)
입력이 임베딩된 후에는 텐서의 형태가 [B, L, D]가 되며, 여기서 D는 임베딩 차원(embedding size)이다.
각 네트워크는 4층 Transformer(Vaswani et al., 2017) 구조를 사용하며, 다음과 같은 특징을 갖는다:
- RMSNorm (Zhang & Sennrich, 2019)
- Bias 없음(no bias) (Chowdhery et al., 2023)
- Rotary embedding (Su et al., 2024)
- SwiGLU 활성 함수(activation function) (Hendrycks & Gimpel, 2016; Shazeer, 2020)
HRM의 의사코드(Pseudocode)
def hrm(z, x, n=2, T=2): # 계층적 추론(hierarchical reasoning)
zH, zL = z
with torch.no_grad():
for i in range(nT - 2):
zL = L_net(zL, zH, x)
if (i + 1) % T == 0:
zH = H_net(zH, zL)
# 1-step gradient 업데이트
zL = L_net(zL, zH, x)
zH = H_net(zH, zL)
return (zH, zL), output_head(zH), Q_head(zH)
def ACT_halt(q, y_hat, y_true):
target_halt = (y_hat == y_true)
loss = 0.5 * binary_cross_entropy(q[0], target_halt)
return loss
def ACT_continue(q, last_step):
if last_step:
target_continue = sigmoid(q[0])
else:
target_continue = sigmoid(max(q[0], q[1]))
loss = 0.5 * binary_cross_entropy(q[1], target_continue)
return loss
# 깊은 감독(Deep Supervision)
for x_input, y_true in train_dataloader:
z = z_init
for step in range(N_sup): # deep supervision 단계
x = input_embedding(x_input)
z, y_pred, q = hrm(z, x)
loss = softmax_cross_entropy(y_pred, y_true)
# Q-learning 기반 적응적 계산 시간(Adaptive Computational Time, ACT)
loss += ACT_halt(q, y_pred, y_true)
_, _, q_next = hrm(z, x) # 추가 forward pass
loss += ACT_continue(q_next, step == N_sup - 1)
z = z.detach()
loss.backward()
opt.step()
opt.zero_grad()
if q[0] > q[1]: # 조기 종료(early stopping)
break그림 2: 계층적 추론 모델(Hierarchical Reasoning Models, HRMs)의 의사코드(pseudocode).

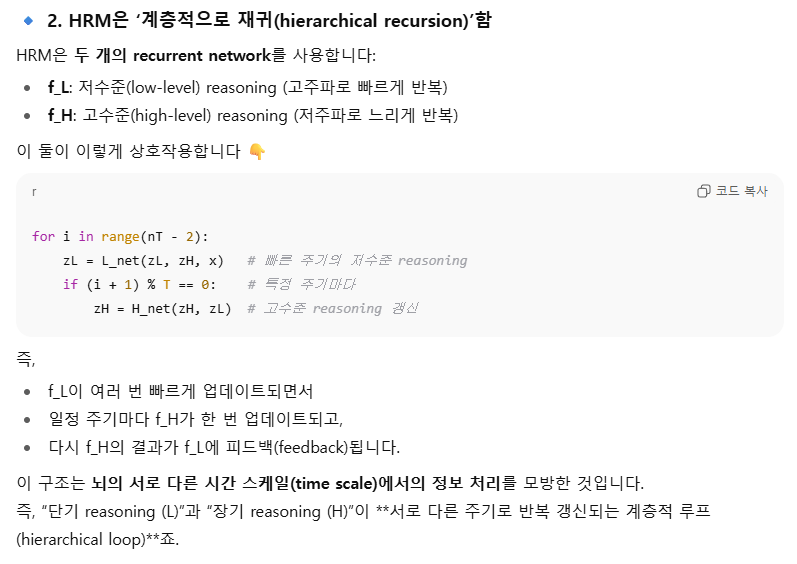

2.2 서로 다른 두 주기(frequency)에서의 재귀(Recursion at two different frequencies)
Wang et al. (2025)이 사용한 하이퍼파라미터 설정은 다음과 같다:
- n = 2 (저수준 네트워크 f_L의 단계 수)
- f_H = 1 (고수준 네트워크 f_H의 단계 수)
- 이를 T = 2회 반복
이 설정을 기준으로 HRM의 한 번의 forward pass는 아래와 같이 수행된다:
x ← f_I(x̃) # 입력 임베딩
z_L ← f_L(z_L + z_H + x) # gradient 없음
z_L ← f_L(z_L + z_H + x) # gradient 없음
z_H ← f_H(z_L + z_H) # gradient 없음
z_L ← f_L(z_L + z_H + x) # gradient 없음
z_L ← z_L.detach() # 그래프에서 분리
z_H ← z_H.detach() # 그래프에서 분리
z_L ← f_L(z_L + z_H + x) # gradient 있음
z_H ← f_H(z_L + z_H) # gradient 있음
ŷ ← argmax(f_O(z_H)) # 최종 예측 출력여기서
- ŷ는 예측된 출력(answer),
- z_L과 z_H는 각각
- 처음에는 임의 초기 임베딩(initialized embeddings)으로 시작하거나,
- 이전 deep supervision 단계의 출력 임베딩을 사용한다. 이때 두 임베딩은 계산 그래프(computational graph)로부터 분리(detach)된 상태로 전달된다.
이 과정을 보면, HRM의 한 번의 순전파(forward pass)는 총 6번의 함수 평가(function evaluation)로 구성된다. 그 중 처음 4번의 함수 호출은 계산 그래프에서 분리되어 역전파(backpropagation)가 이루어지지 않으며, 마지막 2단계만이 gradient를 계산하는 실제 학습 단계로 사용된다.
논문에서는 모든 실험에서 n = 2, T = 2를 사용하지만, 이 구조는 n (저수준 단계 수)와 T (재귀 반복 횟수)를 임의의 값으로 설정하여 일반화할 수 있으며, 이는 Algorithm 2에서 보여진다.
2.3 1-스텝 그래디언트 근사(1-step gradient approximation)를 이용한 고정점 재귀(Fixed-point recursion)
다음과 같이 가정하자. 두 네트워크 f_L, f_H를 반복(recursing)함으로써 잠재 벡터 쌍 (z_L, z_H)이 고정점(fixed-point) (z_L*, z_H*)에 도달한다고 할 때,
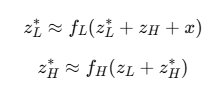
이때, 암묵적 함수 정리(Implicit Function Theorem) (Krantz & Parks, 2002)와 1-스텝 그래디언트 근사(1-step gradient approximation) (Bai et al., 2019)을 적용하여, 마지막 단계의 f_L과 f_H에 대해서만 역전파(backpropagation)를 수행함으로써 gradient를 근사(approximate)한다.
즉, 6단계 중 마지막 2단계만 gradient를 추적하면 충분하다는 것을 이 정리가 수학적으로 정당화해주며, 이를 통해 메모리 사용량을 크게 줄일 수 있다.
2.4 깊은 감독(Deep Supervision)
모델의 유효 깊이(effective depth)를 향상시키기 위해 깊은 감독(Deep Supervision)을 적용한다. 이는 이전 단계의 잠재 표현 (z_H, z_L)을 다음 forward pass의 초기값(initialization)으로 재사용하는 방식이다.
이를 통해 모델은 여러 반복(iteration)을 거치며 점진적으로 추론(reasoning)을 수행하고, 잠재 벡터 z_L과 z_H를 개선해가며 정답에 수렴(converge)할 가능성을 높인다.
최대 N_sup = 16개의 감독 단계(supervision steps)가 사용된다.
2.3절의 핵심은 “모든 재귀 단계의 gradient를 계산하지 않고, 마지막 단계만으로 근사한다”는 개념
2.5 적응적 계산 시간(Adaptive Computational Time, ACT)
깊은 감독(Deep Supervision)을 적용할 때, 각 미니배치(mini-batch)는 다음 배치로 넘어가기 전에 반드시 N_sup = 16단계의 감독 단계(supervision steps)를 모두 수행해야 한다. 이는 계산량이 매우 크며, “소수의 샘플에 대해 많은 단계로 최적화할 것인가” vs “다수의 샘플을 적은 단계로 학습할 것인가” 라는 트레이드오프(trade-off)가 존재한다.
이를 효율적으로 조절하기 위해 HRM은 조기 종료(early stopping) 여부를 판단하는 정지 메커니즘(halting mechanism)을 추가한다. 이 메커니즘은 Q-learning 목표 함수(Q-learning objective)를 통해 학습되며, 이를 위해 z_H를 별도의 헤드(head)에 통과시킨 후 추가적인 forward pass를 수행해 “지금 멈추는 것이 더 나았는가?”를 평가한다.
이 방식을 Adaptive Computational Time (ACT)이라 부른다. ACT는 훈련 시에만 사용되며, 테스트 시에는 모든 N_sup = 16단계를 그대로 수행해 최대 성능을 확보한다.
ACT를 적용하면 예시당 계산 시간이 크게 줄어든다. 예를 들어 Sudoku-Extreme 데이터셋에서는 평균적으로 16단계 대신 2단계 미만만 수행하게 되어, 동일한 학습 반복 횟수 내에서 훨씬 더 많은 데이터 샘플을 커버할 수 있다.
2.6 깊은 감독(Deep Supervision)과 1-step Gradient 근사는 BPTT를 대체한다
깊은 감독과 1-step gradient 근사는 시간적 신용 할당(Temporal Credit Assignment, TCA) 문제(Rumelhart et al., 1985; Werbos, 1988; Elman, 1990)를 해결하기 위한, BPTT(Backpropagation Through Time) (Werbos, 1974; Rumelhart et al., 1985; LeCun, 1985)의 생물학적으로 더 타당하고(computationally plausible) 계산량이 훨씬 적은 대안(alternative)이다.
즉, HRM은 일반적으로 매우 큰 네트워크가 필요로 하는 학습을 전체 깊이에 대한 역전파 없이도 수행할 수 있다는 의미다.
예를 들어, Jang et al. (2023)이 사용한 하이퍼파라미터 설정을 기준으로 하면, HRM은 실질적으로 다음과 같은 깊이로 reasoning을 수행하게 된다:
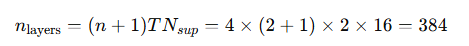
즉, HRM은 384층(effective layers)에 해당하는 깊은 네트워크 효과를 실제 역전파 없이 효과적으로 모사한다.
2.7 HRM 요약(Summary of HRM)
HRM은 서로 다른 주기(frequency)로 동작하는 두 개의 네트워크(고주파 vs 저주파)를 재귀적으로 결합하고, 깊은 감독(Deep Supervision)을 통해 여러 단계에 걸쳐 점진적으로 답변을 개선하는 구조를 갖는다. 또한, ACT(Adaptive Computational Time)을 통해 각 데이터 샘플에 소비되는 계산 시간을 효율적으로 줄인다.
이로써 HRM은 모든 층에 대한 역전파(backpropagation) 없이도 매우 깊은 네트워크의 효과를 모방(imitation)할 수 있으며,
일반적인 지도 학습 모델이 어려워하는 복잡한 질의응답(hard QA) 과제에서 현저히 높은 성능을 달성한다.
그러나 이 방법은 다음과 같은 한계도 있다.
- 구조가 복잡하며 구현 비용이 높고,
- 생물학적 근거(뇌의 주파수 차이 등)에 지나치게 의존하며,
- 고정점 정리(fixed-point theorem)의 적용이 항상 보장되지 않는다.
다음 절에서는 이러한 HRM의 문제점과, 이를 개선할 수 있는 향후 개선 방향(potential improvements)을 논의한다.

3. 계층적 추론 모델(HRM)의 개선 대상(Target for Improvements in HRM)
이 절에서는 Hierarchical Reasoning Model (HRM)의 핵심적인 한계와 개선 가능한 요소들을 정리하고, 이후 제안할 Tiny Recursion Model (TRM)에서 이를 어떻게 해결하는지를 설명한다.
3.1 1-step gradient 근사를 사용한 암묵적 함수 정리(Implicit Function Theorem, IFT)
HRM은 총 6번의 재귀(recursion) 중 마지막 2단계만 역전파(backpropagation)를 수행한다. 저자들은 이를 정당화하기 위해 암묵적 함수 정리(Implicit Function Theorem, IFT)와 1-step gradient 근사(one-step approximation)를 사용한다. IFT에 따르면, 순환 함수(recurrent function)가 고정점(fixed point)에 수렴하는 경우, 그 평형점(equilibrium point)에서 단 한 번의 역전파로도 전체 gradient를 근사할 수 있다.
그러나 이러한 정리를 HRM에 적용하는 데에는 여러 가지 문제가 있다. 가장 중요한 점은 — HRM이 실제로 고정점에 도달한다는 보장이 전혀 없다는 것이다.
일반적으로 깊은 평형 모델(Deep Equilibrium Models, Bai et al., 2019)은 고정점을 만족하는 해
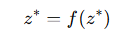
를 찾기 위해 명시적인 고정점 반복(fixed-point iteration)을 수행한다.
반면, HRM은 그러한 반복 과정을 거치지 않고, 단지 f_L과 f_H를 몇 번 forward pass로 실행한 뒤 종료한다. 더욱이 HRM은 단지 4번의 재귀(2회 f_L + 1회 f_H + 1회 f_L)만 수행하고, 이후 바로 “고정점에 도달했다”고 가정한 채 1-step gradient 근사를 적용한다.
즉, HRM은
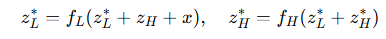
가 성립한다고 가정만 하고, 실제로는 검증 없이 해당 근사를 수행한다.
저자들은 이 근사를 정당화하기 위해 n = 7, T = 7인 경우(자신들의 실험(n=2, T=2)보다 훨씬 깊은 경우)에 대해, 시간이 지남에 따라 forward residual이 점차 감소한다는 예시(Wang et al., 2025, Figure 3)를 제시한다. 그러나 이 경우에도 다음과 같은 문제가 확인된다:
- z_H의 residual은 모든 단계에서 여전히 0보다 명확히 높게 유지된다.
- z_L의 residual은 여러 주기를 거치면서 0에 근접하긴 하지만, 여전히 유의미하게 남아 있다.
- 특히 T번째 주기에서 단 한 번의 f_L 평가 이후, z_L은 고정점에 근접하지 않았음에도 불구하고, 그 시점에서 고정점 도달을 가정하고 1-step gradient 근사를 적용한다.
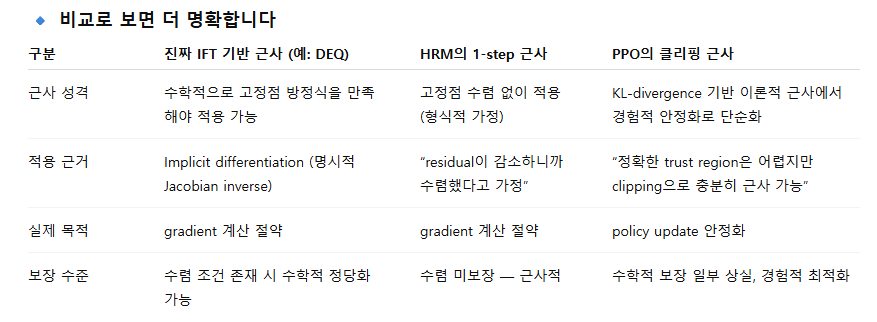
따라서 요약하자면, IFT 정리와 1-step gradient 근사를 HRM에 적용하는 것이 형식적으로 일부 근거는 있을지라도, 실제로는 고정점이 제대로 수렴하지 않은 상태에서 근사를 적용하고 있다는 점에서 그 타당성이 매우 제한적이다.
다음 절에서는 이러한 한계를 해결하기 위해, IFT 정리와 1-step gradient 근사에 의존하지 않고도 동일하거나 그 이상의 효과를 얻을 수 있는 새로운 접근법 — 즉, Tiny Recursion Model (TRM)을 제안한다.
결국 ppo 때처럼 수학적 근사가 아닌 경험적 근사
3.2 적응적 계산 시간(ACT)에 따른 2배의 Forward Pass
HRM은 훈련 과정에서 각 데이터 샘플에 소비되는 시간을 최적화하기 위해 Adaptive Computational Time (ACT)을 사용한다.
ACT가 없다면, 하나의 데이터 샘플에 대해 N_sup = 16단계의 감독(supervision) 과정을 모두 수행해야 하므로 매우 비효율적이다.
ACT는 추가적인 Q-learning 목적 함수(Q-learning objective)를 통해 구현된다. 이 Q-learning 목적은
“현재 샘플 학습을 멈추고 다음 데이터로 넘어갈지, 아니면 같은 데이터를 더 반복 학습할지” 를 결정한다.
이를 통해 훈련 시간을 훨씬 효율적으로 사용할 수 있다. 특히 ACT를 적용하면, 한 데이터 샘플당 평균 감독 단계 수가 매우 낮아지는데 (Wang et al., 2025에서 보고된 결과에 따르면 Sudoku-Extreme 데이터셋의 경우 평균 2단계 미만) 이는 전체 학습 속도를 크게 향상시킨다.
그러나 ACT에는 숨은 비용(hidden cost)이 존재한다. 이 비용은 HRM 논문 본문에는 명시되지 않았지만, 공식 코드(official code)를 보면 분명히 나타난다.
ACT의 Q-learning 목적은 두 가지 손실 항목으로 구성된다.
- Halting loss (멈춤 손실)
- Continue loss (계속 손실)
문제는 이 중 continue loss를 계산하기 위해서는 HRM 전체를 한 번 더 forward pass해야 한다는 점이다. 즉, HRM의 모든 함수(f_L, f_H 등) 6회 평가를 다시 수행해야 한다.
결국 ACT는 각 데이터 샘플당 계산을 더 효율적으로 만들어주지만,
매번의 최적화 단계(optimization step)에서 2회의 forward pass가 필요하다는 대가를 치르게 된다.
이 구체적인 수식화(formulation)는 Algorithm 2에 제시되어 있다.
다음 절에서는, 이러한 ACT의 2회 forward pass 구조 자체를 필요로 하지 않도록 이를 완전히 대체(bypass)할 수 있는 새로운 접근법을 제안한다.
3.3 복잡한 생물학적 논리에 기반한 계층적 해석(Hierarchical interpretation based on complex biological arguments)
HRM의 저자들은 서로 다른 계층(hierarchy)에서 작동하는 두 개의 잠재 변수(latent variable)와 두 개의 네트워크(f_L, f_H)를 사용하는 이유를 생물학적 근거(biological arguments)로 설명한다. 즉, 인공 신경망과는 거리가 먼, 실제 뇌의 구조적/시간적 계층 처리 메커니즘을 모델링하려 시도한 것이다.
그들은 심지어 HRM의 구조를 실제 생쥐의 뇌 실험 데이터와 비교하여 대응시키려 하기도 했다. 물론 흥미로운 시도이긴 하지만, 이런 방식의 설명은 HRM의 설계 의도를 논리적으로 이해하기 매우 어렵게 만든다.
게다가 논문에는 소거 실험(ablations)이 거의 없어,
- 어떤 부분이 실제 성능 향상에 기여하는지,
- 왜 두 개의 잠재 변수만 사용했는지,
- 왜 이 두 네트워크가 서로 다른 주기로 반복되어야 하는지
를 명확히 구분하기 어렵다.
결국, HRM은 생물학적 논리와 고정점 정리(fixed-point theorem)에 지나치게 의존하고 있으며, 이 두 요소 모두 HRM의 실제 동작 원리와 직접적인 관련성이 충분히 검증되지 않았다.
다음 절에서는 이러한 복잡한 생물학적 논리나 수학적 전제 없이, 재귀적 과정(recursive process) 자체를 훨씬 단순하고 명확하게 해석할 수 있는 새로운 접근법을 제시한다.
이 방법은
- 생물학적 근거도,
- 고정점 정리도,
- 계층적 구조도,
- 두 개의 별도 네트워크(f_L, f_H)도 필요하지 않다.
또한, 왜 잠재 변수의 개수가 정확히 두 개(z_L, z_H)일 때 가장 효율적인지도 자연스럽게 설명된다.
def latent_recursion(x, y, z, n=6):
for i in range(n): # 잠재 추론(latent reasoning)
z = net(x, y, z)
y = net(y, z) # 출력 답변을 점진적으로 개선
return y, z
def deep_recursion(x, y, z, n=6, T=3):
# y와 z를 개선하기 위해 T-1회 재귀 수행 (gradient 불필요)
with torch.no_grad():
for j in range(T - 1):
y, z = latent_recursion(x, y, z, n)
# 마지막 1회는 gradient 포함
y, z = latent_recursion(x, y, z, n)
return (y.detach(), z.detach()), output_head(y), Q_head(y)
# 깊은 감독(Deep Supervision)
for x_input, y_true in train_dataloader:
y, z = y_init, z_init
for step in range(N_supervision):
x = input_embedding(x_input)
(y, z), y_hat, q_hat = deep_recursion(x, y, z)
loss = softmax_cross_entropy(y_hat, y_true)
loss += binary_cross_entropy(q_hat, (y_hat == y_true))
loss.backward()
opt.step()
opt.zero_grad()
if q_hat > 0: # 조기 종료(early-stopping)
break그림 3: Tiny Recursion Model (TRM)의 의사코드(pseudocode). TRM은 HRM의 복잡한 2계층 구조를 단일 재귀 네트워크로 단순화하면서, 생물학적 전제 없이도 동일한 또는 더 높은 수준의 일반화 성능을 달성한다.
4. Tiny Recursion Models (TRM)
이 절에서는 Tiny Recursion Model (TRM)을 제안한다. HRM과 달리, TRM은 복잡한 수학적 정리나 계층 구조, 생물학적 논리를 전혀 필요로 하지 않는다. 그럼에도 불구하고 일반화 성능(generalization)은 오히려 더 뛰어나며,
- 두 개의 중간 크기 네트워크 대신 단 하나의 초소형 네트워크,
- ACT(Adaptive Computational Time) 수행 시에도 2번이 아닌 단 1번의 forward pass만으로 작동한다.
제안하는 접근법은 Algorithm 3에 기술되어 있으며, 그림 1에 시각적으로 요약되어 있다. 또한 표 1에서는 Sudoku-Extreme 데이터셋(1K개의 훈련 예시, 42만 3천 개의 테스트 예시)에서의 소거 실험(ablation study) 결과를 제시한다. 이후 각 구성 요소별로 TRM의 핵심 아이디어를 자세히 설명한다.
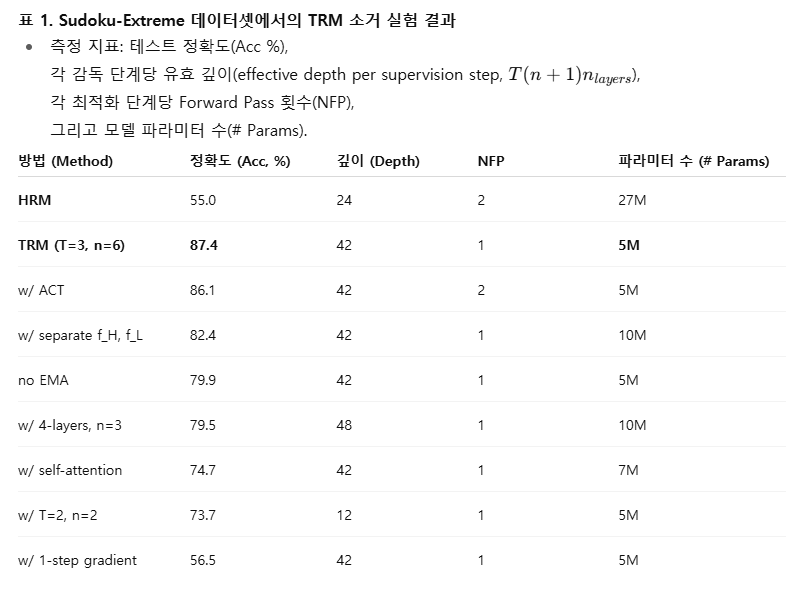
요약하자면:
TRM은 HRM 대비
- 5배 이상 적은 파라미터(27M → 5M),
- 한 번의 forward pass로 작동,
- 더 깊은 유효 추론 깊이(Depth = 42)를 가지면서도
- Sudoku-Extreme 정확도를 55% → 87.4%로 대폭 향상시켰다.
즉, TRM은 구조적 단순화와 계산 효율성, 일반화 성능을 동시에 달성한 모델이다.
4.1 고정점 정리(Fixed-point theorem)가 필요하지 않음
HRM은 1-step gradient 근사(approximation) (Bai et al., 2019)을 적용하기 위해, 두 잠재 변수 z_L과 z_H가 각각 고정점(fixed point)에 수렴한다고 가정한다. 이 가정 덕분에 HRM은 마지막 두 번의 함수 평가(1회 f_L, 1회 f_H)에 대해서만 역전파(backpropagation)를 수행할 수 있다고 주장한다.
하지만 TRM은 이러한 이론적 가정(theoretical requirement) 자체를 제거한다. 대신, 우리는 하나의 완전한 재귀 과정(full recursion process)을 다음과 같이 정의한다. 이 과정은 f_L을 n회, f_H를 1회 평가(evaluation)하는 구조를 가진다:
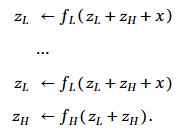
그리고 TRM은 이 전체 재귀 과정을 그대로 역전파에 포함시켜(back-propagate through) 학습한다.
깊은 감독(Deep Supervision)을 통해 모델은 어떤 초기 상태의 잠재 변수 쌍 (z_L, z_H)이 주어지더라도, 이 완전한 재귀 과정(full recursion)을 거쳐 점진적으로 개선되도록 학습된다. 즉, 학습 목표가 “재귀 과정을 거치며 z_H를 해답에 더 가깝게 만들라”이므로, gradient가 없어도 여러 번의 재귀를 수행하는 것만으로도 해결 방향으로 수렴하게 된다.
따라서 TRM은 HRM처럼
- 1-step gradient 근사를 사용할 필요도 없고,
- 고정점에 도달했다고 가정할 필요도 없다. 즉, 암묵적 함수 정리(IFT)를 전혀 사용하지 않아도 된다.
그럼에도 불구하고, 여전히 여러 번의 gradient-free 재귀 과정을 통해 잠재 변수 (z_L, z_H)를 개선할 수 있다.
이 접근 방식을 통해 TRM은 Sudoku-Extreme 데이터셋에서 일반화 성능을 크게 향상시켰다 — 정확도가 56.5% → 87.4%로 상승하였다(표 1 참조).
4.2 z_H와 z_L의 단순한 재해석(Simpler reinterpretation of z_H and z_L)
HRM은 생물학적 논리에 따라 서로 다른 계층(hierarchy)에 속한 두 개의 잠재 특징(z_H, z_L)을 사용하여 계층적 추론(hierarchical reasoning)을 수행한다고 해석된다. 그러나 다음과 같은 근본적인 의문이 제기된다.
“왜 잠재 특징을 꼭 두 개만 써야 할까? 하나나 세 개 이상은 안 되는가?”
“굳이 생물학적 근거를 들어야만 이 ‘계층적’ 특징을 설명할 수 있는가?”
이에 대해 우리는 생물학과 무관한, 훨씬 단순하고 자연스러운 해석을 제안하며, 이 설명은 “왜 두 개의 특징이 필요한가”라는 질문에 직접적으로 답한다.
핵심 아이디어
사실상,
- z_H는 단순히 “현재의 (임베딩된) 해답(current embedded solution)”을 의미한다. 출력 헤드(output head)를 통과시키고, argmax 연산을 통해 가장 가까운 토큰으로 반올림하면 실제 해답 형태로 복원할 수 있다.
- 반면 z_L은 직접적으로 해답을 나타내지는 않지만, 다음 함수를 통해 해답 형태로 변환할 수 있는 잠재적 추론 표현(latent reasoning feature)이다.
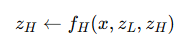
그림 6의 Sudoku-Extreme 예시에서 확인할 수 있듯이, z_H는 실제 해답과 일치하지만 z_L은 그렇지 않다.
이 해석이 의미하는 바
이제 계층 구조(hierarchy)는 필요 없다.
모델은 단순히
- 입력 x,
- 현재 해답 y (기존 z_H),
- 잠재 추론 표현 z (기존 z_L) 를 사용해 동작한다고 보면 된다.
모델은 입력 x, 현재 해답 y, 현재 잠재 추론 z를 받아 재귀적으로 z를 개선하고, 그 다음 현재 z와 이전 해답 y를 바탕으로 새로운 해답 y를 제안한다. 이미 충분히 정확하면 기존 해답을 그대로 유지한다.
왜 두 개의 특징(y, z)이 필요한가
이 재해석은 알고리즘의 수학적 구조를 바꾸지는 않지만, 매우 단순하고 자연스러운 설명을 제공한다.
- 질문 x, 이전의 추론 z, 그리고 이전 해답 y를 함께 기억하면, 모델은 다음 단계의 추론 z와 다음 해답 y를 더 잘 개선할 수 있다.
- 만약 이전의 추론 z를 전달하지 않는다면, 모델은 이전 해답 y에 도달한 과정을 잊게 된다. 즉, z가 chain-of-thought(사고의 연쇄) 역할을 하기 때문에 필수적이다.
- 반대로 이전의 해답 y를 전달하지 않으면, 모델은 현재 해답이 무엇인지 기억할 수 없고, 해답 y 자체를 z 내부에 저장하려고 하게 된다. 이렇게 되면 z가 본래의 “추론(latent reasoning)” 기능을 잃는다.
따라서 y와 z를 분리해서 유지하는 것이 필수적이며, z를 여러 개의 특징으로 쪼갤 이유도 없다.
다른 특징 개수 실험 (Table 2)
직관적으로는 납득이 되지만, 우리는 실제로 “특징(feature) 개수를 늘리거나 줄이는 것”이 도움이 되는지 검증했다. 그 결과는 아래 표 2와 같다.
더 많은 특징(>2)
z를 여러 특징으로 분할하여, 각 재귀 단계에서 서로 다른 z_i (i=1,…,n)을 생성하고 각 z_i를 다음 감독 단계로 전달하도록 실험했다 (Algorithm 5 참고). 그 결과 성능이 오히려 하락했다. 이는 이미 설명했듯, z를 여러 부분으로 나눌 필요가 없기 때문이다. 즉, 계층 구조는 불필요하다.
하나의 특징(1)
반대로, 단일 특징만 사용하는 실험도 진행했다. 즉, z_H 하나만 감독 단계 간에 전달하도록 설정했다 (Algorithm 4 참고).
그 결과 역시 성능이 하락했다. 이는 z가 해답 y까지 함께 저장해야 하므로, 추론 기능이 손상되기 때문으로 보인다.
결론
Sudoku-Extreme 데이터셋에서의 실험 결과, 잠재 변수는 y와 z 두 개만 사용하는 것이 가장 단순하면서도 정확도가 높았다.

4.3 단일 네트워크(Single network)
HRM은 두 개의 네트워크를 사용한다.
- 하나는 저수준 모듈 f_L로서 자주 반복적으로 적용되고,
- 다른 하나는 고수준 모듈 f_H로서 드물게 적용된다.
이 때문에 HRM은 단일 네트워크를 사용하는 일반적인 지도학습(supervised learning)보다 두 배의 파라미터 수를 필요로 한다.
앞서 언급했듯이,
- f_L은 잠재 추론 특징(latent reasoning feature) z (HRM의 z_L)를 반복적으로 갱신하고,
- f_H는 잠재 추론과 현재 해답을 기반으로 해답 y (HRM의 z_H)를 갱신하는 역할을 한다.
여기서 중요한 점은,
- z ← f_L(x + y + z) 는 입력 x를 포함하지만,
- y ← f_H(y + z) 는 x를 포함하지 않는다는 것이다.
즉, 입력에 x가 포함되느냐 여부가 “잠재 추론(z)을 반복적으로 갱신하는 역할인지” 아니면 “잠재 추론(z)을 사용해 해답(y)을 갱신하는 역할인지”를 자연스럽게 구분해준다.
이 관찰을 바탕으로, 우리는
“두 개의 네트워크를 하나의 네트워크로 통합해도 같은 역할을 수행할 수 있지 않을까?” 라는 가능성을 탐색했다.
실험 결과, 단일 네트워크로 두 역할을 동시에 수행하도록 설계했을 때, Sudoku-Extreme 데이터셋에서 일반화 성능이 개선되었다 — 정확도는 82.4% → 87.4%로 상승하였으며 (표 1 참조), 파라미터 수는 절반으로 감소하였다.
즉, 결론적으로 하나의 네트워크면 충분하다(single network is enough)는 것이 확인되었다.
4.4 적을수록 더 좋다(Less is more)
우리는 모델의 용량(capacity)을 늘리기 위해 층 수(layers)를 증가시켜 모델을 확장(scale-up)해보았다. 그러나 놀랍게도, 층 수를 늘리면 오히려 과적합(overfitting)이 발생하여 일반화 성능이 감소하였다.
반대로, 층 수를 줄이면서(recursive step 수 n은 비례적으로 늘려) 계산량과 유효 깊이(effective depth)가 비슷하도록 조정한 결과, 4층 대신 2층(two-layer)을 사용하는 것이 가장 높은 일반화 성능을 보였다.
그 결과, Sudoku-Extreme에서 정확도가 79.5% → 87.4%로 상승하였으며 (표 1 참조), 파라미터 수도 다시 절반으로 감소하였다.
작은 네트워크가 더 좋은 결과를 내는 것은 의외이지만, 실험적으로 2층 구조가 최적임이 확인되었다.
이와 유사하게, Bai & Melas-Kyriazi (2024)도 깊은 평형(diffusion) 모델에서 2층 구조가 최적 성능을 낸다고 보고한 바 있다.
다만 그들의 경우 큰 네트워크와 성능이 유사한 수준이었으나, TRM에서는 2층이 명확히 더 높은 성능을 보였다.
이는 현대 신경망의 일반적인 경향 — “모델 크기가 클수록 일반화가 좋아진다” — 와는 상반되어 보인다. 하지만 데이터가 충분히 많지 않을 때, 큰 모델은 오히려 과적합 패널티(overfitting penalty)를 받게 된다(Kaplan et al., 2020).
결국 이는 데이터의 부족(data scarcity)을 의미하며, 이 상황에서는
작은 네트워크 + 깊은 재귀(deep recursion) + 깊은 감독(deep supervision) 구조가 과적합을 효과적으로 회피하면서 우수한 일반화 성능을 달성할 수 있음을 시사한다.
4.5 작은 고정 길이 컨텍스트(task)에 적합한 Attention-Free 아키텍처
Self-Attention은 일반적으로 긴 컨텍스트 길이(L ≫ D)를 다룰 때 매우 효과적이다. 이는 시퀀스 전체를 고려하면서도, 단지 [D, 3D] 크기의 파라미터 행렬만 필요하기 때문이다.
하지만 컨텍스트 길이 L이 작거나 고정된 경우(L ≤ D)에는 단순한 선형 계층(linear layer)이 훨씬 효율적이다. 이 경우 필요한 파라미터는 [L, L] 행렬 하나뿐이기 때문이다.
이에 착안해, 우리는 MLP-Mixer (Tolstikhin et al., 2021)에서 영감을 받아 Self-Attention 층을 시퀀스 길이 방향으로 적용되는 MLP로 대체하였다.
즉, Self-Attention → MLP 변환을 적용한 결과, Sudoku-Extreme 데이터셋에서 일반화 성능이 크게 향상되었다 — 정확도는 74.7% → 87.4%로 상승하였다(표 1 참조).
이 접근법은 9x9 Sudoku와 같은 작고 고정된 컨텍스트 길이를 가진 문제에서 특히 효과적이었다. 그러나 Maze-Hard나 ARC-AGI (30x30 grid)와 같이 컨텍스트 길이가 큰 문제에서는 최적이 아니었다.
따라서 모든 실험에 대해 Self-Attention을 사용한 경우와 사용하지 않은 경우를 함께 비교하여 결과를 보고하였다.
4.6 ACT에서 추가 Forward Pass 불필요
앞서 언급했듯, HRM에서의 ACT(Adaptive Computational Time) 구현은 Q-learning 기반의 continue loss를 포함하기 때문에 매 학습 단계마다 두 번의 forward pass가 필요하며, 이는 학습 속도를 느리게 만든다.
이에 우리는 매우 단순한 해결책을 제안한다:
Q-learning의 continue loss 항목을 완전히 제거하고, 단순히 “정답에 도달했는가”에 대한 Binary Cross-Entropy(BCE) 손실을 통해 정지 확률(halting probability)만 학습한다.
즉,
- continue loss 제거 → 두 번째 forward pass 제거,
- 여전히 올바른 종료 시점 판단 가능.
이 방법을 적용한 결과, 학습 시간은 크게 단축되었으며, 일반화 성능 차이도 거의 없었다 — 정확도는 86.1% → 87.4%로 오히려 약간 향상되었다(표 1 참조).
4.7 지수 이동 평균(Exponential Moving Average, EMA)
작은 데이터셋(예: Sudoku-Extreme, Maze-Hard)에서는 HRM이 빠르게 과적합(overfitting)된 뒤 발산(divergence)하는 문제가 있었다.
이를 완화하고 학습 안정성을 높이기 위해, 우리는 가중치(weight)의 지수 이동 평균(EMA, Exponential Moving Average)을 적용했다. 이는 GAN(Brock et al., 2018)이나 Diffusion 모델(Song & Ermon, 2020)에서도 학습 안정화에 자주 사용되는 기법이다.
EMA를 적용한 결과,
- 급격한 학습 붕괴(sharp collapse)를 방지하고,
- 일반화 성능이 향상되었다 — 정확도는 79.9% → 87.4%로 상승하였다(표 1 참조).
즉, EMA는 소규모 데이터셋에서 HRM/TRM의 안정성과 성능을 모두 향상시키는 핵심 요소로 작용한다.
4.8 재귀 횟수의 최적화 (Optimal number of recursions)
우리는 재귀 횟수(T와 n)를 다양하게 바꾸며 실험을 진행한 결과, Sudoku-Extreme 데이터셋에서 다음 설정이 최적의 일반화 성능을 보였다.
- HRM: T = 3, n = 3 → (총 48회 재귀 수행)
- TRM: T = 3, n = 6 → (총 42회 재귀 수행)
더 많은 재귀를 수행하면 더 어려운 문제에서는 도움이 될 가능성이 있지만 (자원 제약으로 인해 추가 실험은 진행하지 못했다), T나 n을 늘릴수록 계산 속도가 급격히 느려진다.
표 3은 HRM과 TRM 각각에서 n과 T를 변화시켰을 때의 결과를 보여준다. TRM은 전체 재귀 과정에 대해 backpropagation을 수행하기 때문에, n이 지나치게 커질 경우 메모리 초과(Out Of Memory, OOM)가 발생한다. 그러나 이러한 메모리 비용은 그만한 가치가 있을 정도로 성능 향상이 매우 크다.
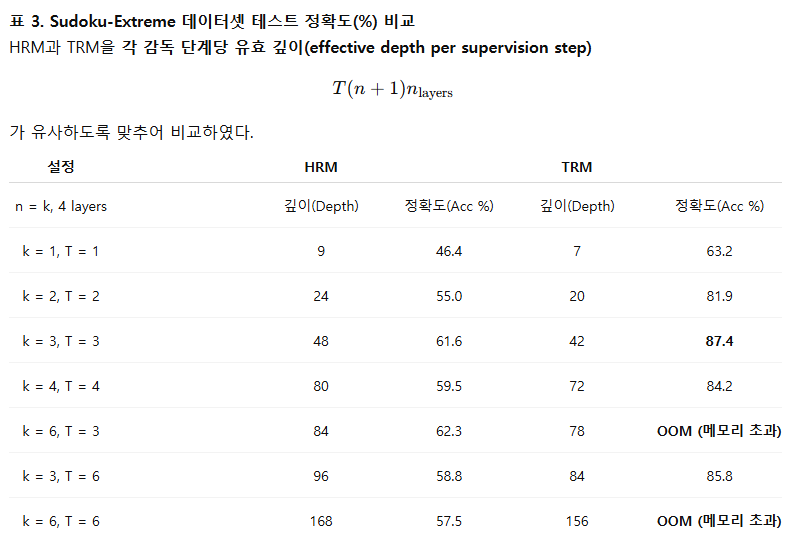
결론적으로, TRM은 적절한 재귀 깊이(T=3, n=6)에서 가장 우수한 성능(87.4%)을 달성하며, 이는 HRM보다 훨씬 적은 계산 비용으로 더 높은 일반화 성능을 보여준다.
다음 절에서는, 여러 데이터셋에서 HRM, TRM, 그리고 LLM을 비교한 주요 실험 결과(main results)를 제시한다.
5. 결과(Results)
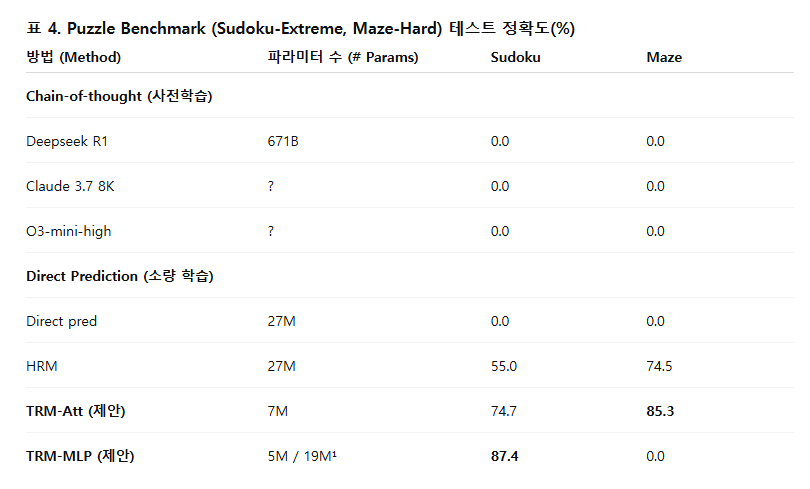
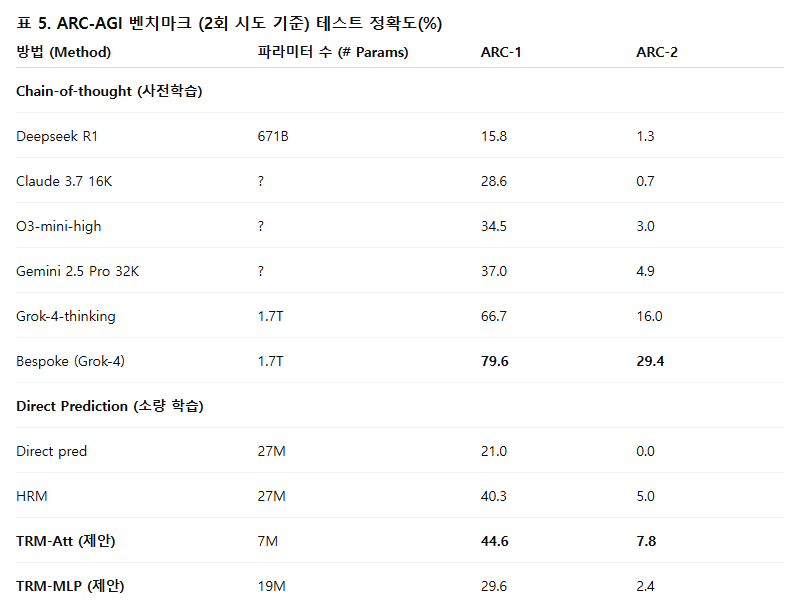
Wang et al. (2025)를 따라, 우리는 다음 네 가지 데이터셋에서 TRM을 평가하였다: Sudoku-Extreme (Wang et al., 2025), Maze-Hard (Wang et al., 2025), ARC-AGI-1 (Chollet, 2019), ARC-AGI-2 (Chollet et al., 2025).
결과는 표 4와 표 5에 제시되어 있으며, 하이퍼파라미터 설정은 Hyper-parameters and setup 절에, 각 데이터셋 설명은 아래에 정리하였다.
데이터셋 설명
- Sudoku-Extreme
매우 난이도 높은 9x9 스도쿠 퍼즐(Dillion, 2025; Palm et al., 2018; Park, 2018)로 구성되어 있으며, 훈련 데이터는 단 1K개만 사용하여 소량 학습(small-sample learning) 능력을 평가한다. 테스트는 423K개의 퍼즐에서 수행된다. - Maze-Hard
Lehnert et al. (2024)의 절차로 생성된 30x30 미로 데이터셋으로, 최단 경로 길이가 110 이상인 어려운 미로들이다. 훈련 세트와 테스트 세트 모두 1000개의 미로로 구성되어 있다. - ARC-AGI-1 및 ARC-AGI-2
금전적 상금이 걸린 지각 기반(geometric) 퍼즐 데이터셋이다. 각 퍼즐은 인간에게는 비교적 쉽지만, 현재의 AI 모델에게는 매우 어렵다. 각 과제(task)는 2~3개의 입력–출력 예시(pair)와 1~2개의 테스트 입력으로 구성된다. 모델이 두 번의 시도 내에 올바른 출력을 생성한 비율이 최종 점수(accuracy)로 계산된다.
최대 격자 크기는 30x30이다.- ARC-AGI-1: 800개 과제
- ARC-AGI-2: 1120개 과제
또한 ConceptARC (Moskvichev et al., 2023)의 160개 과제를 추가하여 학습 데이터를 보강하였다. 결과는 공개 평가 세트(public evaluation set)에서 보고된다.
데이터 증강 (Data Augmentation)
이들 데이터셋은 매우 작기 때문에, 일반화 성능을 높이기 위해 강력한 데이터 증강(data augmentation)을 적용하였다.

Dihedral 변환은 90도 회전, 수평/수직 반전, 대칭(reflection)을 포함한다.
결과 요약
- TRM (Self-Attention 미사용)
Sudoku-Extreme에서 최고의 일반화 성능 (87.4% test accuracy) 달성. - TRM (Self-Attention 사용)
큰 입력 크기(30x30 grid)를 가지는 과제들에서는 오히려 더 우수한 일반화 성능을 보였다. 이는 MLP의 과적합(overcapacity) 및 Self-Attention의 귀납적 편향(inductive bias) 때문으로 보인다.
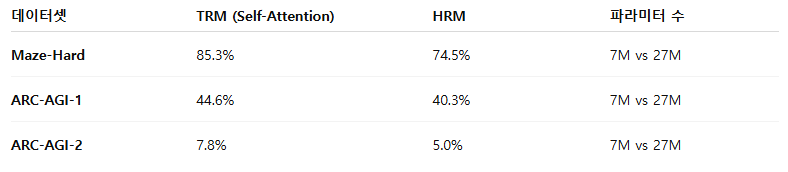
TRM은 HRM보다 4배 적은 파라미터(27M → 7M)로도 모든 과제에서 더 높은 정확도를 기록했다.
6. 결론 (Conclusion)
우리는 Tiny Recursion Model (TRM)을 제안했다. 이는 단 하나의 작은 네트워크가 잠재 추론(latent reasoning)을 반복적으로 개선해 복잡한 문제에서도 강력한 일반화 성능을 달성하는 간단한 재귀적 추론 방법이다.
Hierarchical Reasoning Model (HRM)과 달리 TRM은
- 고정점 정리(fixed-point theorem),
- 복잡한 생물학적 근거,
- 계층 구조(hierarchy) 를 전혀 필요로 하지 않는다.
TRM은
- 층 수를 절반으로 줄이고,
- 두 개의 네트워크를 하나로 통합하며,
- 추가 forward pass를 제거하여 halting 과정을 단순화함으로써 훨씬 단순한 구조로 더 높은 일반화 성능을 달성한다.
논의 (Discussion)
TRM은 네 가지 벤치마크에서 일관되게 HRM보다 뛰어난 일반화 성능을 보였으나, 모든 설정이 모든 데이터셋에 최적이라는 보장은 없다.
예를 들어,
- Self-Attention을 MLP로 대체한 경우, Sudoku-Extreme에서는 테스트 정확도가 10% 향상되었지만, 다른 데이터셋에서는 오히려 성능이 떨어졌다.
즉, 문제 유형에 따라 최적 구조나 파라미터 수가 달라질 수 있으며, 이를 위해 Scaling Law에 기반한 체계적 파라미터 설정이 필요하다.
또한, TRM이 큰 네트워크보다 더 좋은 일반화를 보이는 이유 — 즉, 왜 “재귀(recursion)”가 단순히 네트워크를 깊게 만드는 것보다 훨씬 효과적인가 — 는 아직 명확히 이론적으로 설명되지 않는다. 우리는 과적합 억제 효과 때문이라고 추정하지만, 이를 뒷받침할 이론적 근거는 없다.
논문 마지막 부분(“Ideas that failed”)에서는 시도했으나 효과가 없었던 아이디어들도 간략히 언급한다.
현재 HRM과 TRM은 지도학습 기반의 추론 모델(supervised reasoning model)이며, 생성형(generative) 모델은 아니다. 즉, 주어진 입력에 대해 단 하나의 결정적(deterministic) 출력만을 생성한다. 그러나 실제로는 한 문제에 대해 여러 해답이 존재할 수 있으므로, 향후 TRM을 생성형 과제(generative task)로 확장하는 것이 유의미한 연구 방향일 것이다.
감사의 글 (Acknowledgements)
이 연구를 끝까지 밀어주고 지지해준 Emy Gervais에게 깊은 감사를 전합니다. 본 연구는 Mila와 Digital Research Alliance of Canada가 제공한 컴퓨팅 자원, 소프트웨어, 기술 지원의 도움으로 수행되었습니다.
'인공지능' 카테고리의 다른 글
| DoPE: Denoising Rotary Position Embedding (2) | 2025.11.30 |
|---|---|
| INT v.s. FP: A Comprehensive Study of Fine-Grained Low-bit Quantization Formats (2) | 2025.11.23 |
| Vision-Zero: Scalable VLM Self-Improvement via Strategic Gamified Self-Play (2) | 2025.10.06 |
| Polynomial Composition Activations: Unleashing the Dynamics of Large Language Models (6) | 2025.08.26 |
| DINOv3 (2) | 2025.08.19 |