현재 다음의 대회를 참가하고, 추가로 참가하는 대회가 있어 시간이 많이 밀렸다.
https://junhan-ai.tistory.com/65
Lux AI Season 2 결과
27등
junhan-ai.tistory.com
추가로 참가하고 있는 대회는 BirdCLEF 2023과 Predict Student Performance from Game Play이다.
여튼 개인적인 사정은 여기까지하고 이전에 진행했던, CNN 파트를 이어서 진행하고자 한다.
우리는 이전에 나온 유명한 CNN Architecture들을 살펴볼 것이다. 이것이 왜 중요하냐면 현재도 코드에서 backbone 부분으로, 이미지나 데이터의 특성을 추출하는 역할 수행하는 경우가 많기 때문이다. (일반적으로 딥러닝 모델은 전체 아키텍처를 구성하는 두 가지 주요 구성 요소 backbone과 head가 있으며, 헤드는 백본에서 추출된 특성을 사용하여 최종 출력을 생성한다.)
우리가 살펴볼 CNN Architectures는 AlexNet, VGG, GoogLeNet, ResNet이다. 여기에는 안나와있지만 efficientnet도 자주 사용된다. 내 경험상으로는 ResNet과 efficientnet이 ImageNet 데이터셋으로 사전 훈련된 가중치를 가지고 있는 것을 많이 봤다. (Kaggle 기준)
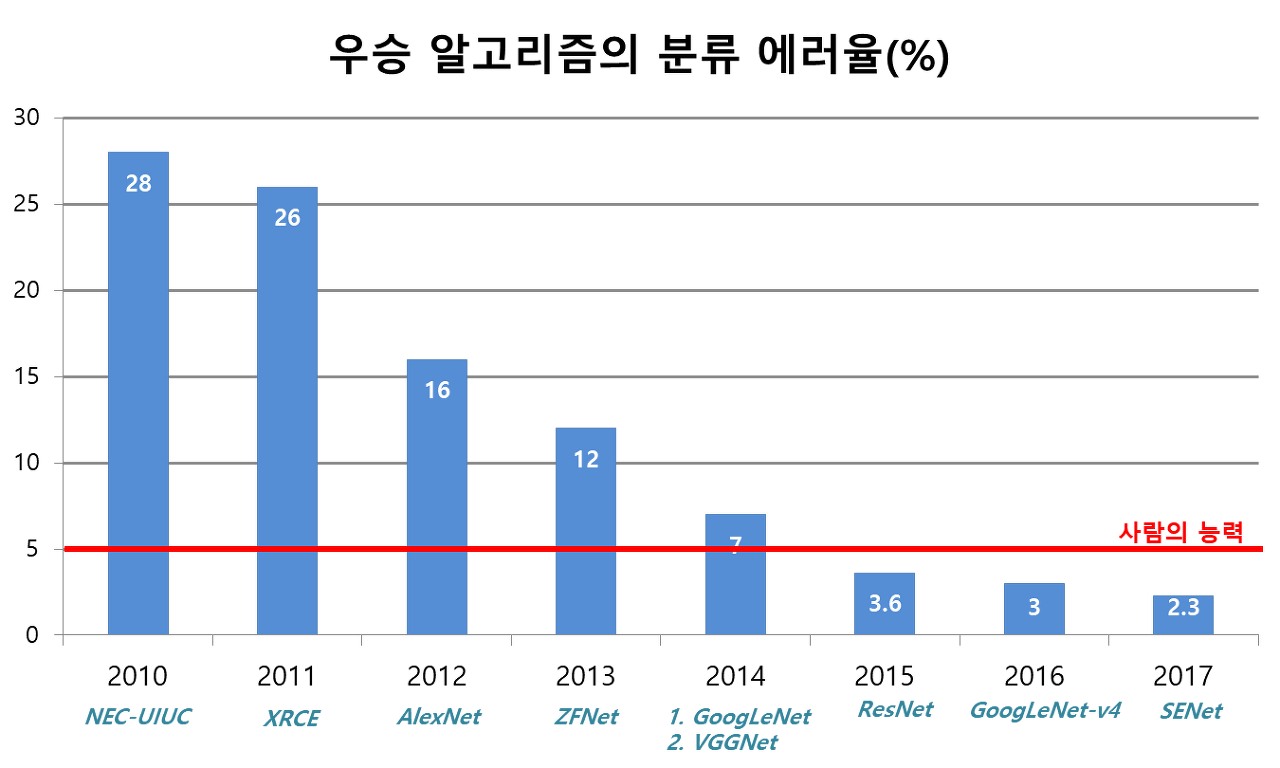
기본적으로 ImageNet Large Scale Visual Recognition Challenge (ILSVRC)의 우승자들의 구조이며 우승자들의 모델은 다음과 같다.
LeNet-5
LeNet-5는 1998년에 제안된 초기의 딥러닝 모델이며 Yann LeCun, Léon Bottou, Yoshua Bengio, and Patrick Haffner에 의해 개발되었습니다. 여기서 Yann LeCun은 굉장히 유명하신 분으로 기억한다.

LeNet-5의 아키텍처는 단순하지만 효과적이며, 주로 숫자 이미지를 분류하는 데 사용된다. 아래는 LeNet-5의 주요 구성 요소와 기능에 대한 설명이다:
- 입력 레이어 (Input Layer):
- 2D 이미지 데이터를 입력으로 받습니다.
- 보통 32x32 크기의 흑백 이미지가 사용됩니다.
- 합성곱 레이어 (Convolutional Layers):
- LeNet-5는 두 개의 합성곱 레이어를 포함합니다.
- 합성곱 연산을 통해 입력 이미지의 지역적인 특징을 추출합니다.
- 활성화 함수로는 시그모이드나 하이퍼볼릭 탄젠트 함수를 사용합니다.
- 서브샘플링 레이어 (Subsampling Layers):
- 합성곱 레이어의 출력을 다운샘플링하여 공간적인 크기를 줄입니다.
- 주로 최대 풀링(max pooling)이 사용되며, 입력 영역에서 가장 큰 값을 선택하여 출력합니다.
- 이를 통해 추출된 특징 맵의 크기를 줄이고, 계산량을 감소시킵니다.
- 완전 연결 레이어 (Fully Connected Layers):
- 완전 연결층은 추출된 특징에 기반하여 분류를 수행합니다.
- 여러 개의 뉴런으로 구성되어 있으며, 출력값을 계산하기 위해 가중치와 편향을 사용합니다.
- 마지막 완전 연결층은 소프트맥스 활성화 함수를 사용하여 확률 분포를 출력합니다.
LeNet-5는 손으로 쓴 숫자 데이터셋인 MNIST를 학습하는 데 많이 사용되었고, 이후에는 더 복잡한 CNN 아키텍처가 개발되었지만, LeNet-5는 딥러닝의 초기 모델로서 중요한 역할을 한 것으로 인정받고 있다.
AlexNet
AlexNet은 2012년에 알렉스 크리즈마(Crizma) 및 팀에서 개발된 딥러닝 모델로, 이미지 인식 대회인 ImageNet Large Scale Visual Recognition Challenge (ILSVRC)에서 우승을 차지하며 큰 주목을 받게된 모델이다.

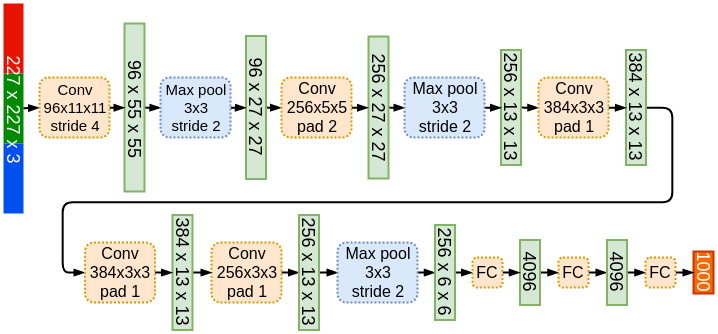
다음은 AlexNet의 주요 특징과 구성 요소에 대한 설명이다:
- 깊은 신경망 구조 (Deep Neural Network Architecture):
- AlexNet은 기존의 얕은 신경망과 비교하여 더 깊은 구조를 가지고 있었습니다.
- 총 8개의 계층으로 구성되어 있으며, 이 중 5개는 합성곱 계층(Convolutional Layer)이고, 3개는 완전 연결 계층(Fully Connected Layer)입니다.
- 합성곱 계층 (Convolutional Layers):
- AlexNet은 5개의 합성곱 계층을 가지고 있으며, 2개의 완전 연결 계층 이전에 배치되어 있습니다.
- 각 합성곱 계층은 여러 개의 필터를 사용하여 이미지에서 특징을 추출합니다.
- ReLU(Rectified Linear Unit) 활성화 함수를 사용하여 비선형성을 도입합니다.
- 최대 풀링 계층 (Max Pooling Layers):
- 합성곱 계층 뒤에는 최대 풀링 계층이 따라옵니다.
- 최대 풀링은 입력 영역에서 가장 큰 값을 선택하여 출력합니다.
- 공간적인 크기를 줄이고, 계산량을 감소시키는 효과를 가지고 있습니다.
- 완전 연결 계층 (Fully Connected Layers):
- 마지막 3개의 계층은 완전 연결 계층으로 구성되어 있습니다.
- 이 계층들은 추출된 특징에 기반하여 이미지를 분류하고, 클래스 예측을 수행합니다.
- 마지막 계층은 소프트맥스 활성화 함수를 사용하여 클래스 확률을 출력합니다.
- 드롭아웃 (Dropout):
- AlexNet은 드롭아웃 기법을 사용하여 과적합을 줄이는 정규화(regularization)를 수행합니다.
- 드롭아웃은 학습 중에 무작위로 일부 뉴런을 비활성화시키는 것으로, 모델의 일반화 성능을 향상시킵니다.
AlexNet은 다음과 같은 공헌을 인정받았다.
- ReLU의 처음 사용:
- AlexNet은 처음으로 ReLU(Rectified Linear Unit) 활성화 함수를 사용한 모델입니다.
- ReLU는 입력이 0보다 작을 때는 0을 출력하고, 0보다 클 때는 입력 값을 그대로 출력하는 함수입니다.
- 이를 통해 비선형성을 도입하고, 모델의 표현 능력을 향상시켰습니다.
- Norm 레이어 사용:
- AlexNet은 Norm 레이어를 사용했으나, 현재는 더 이상 흔하게 사용되지 않습니다.
- Norm 레이어는 정규화(normalization) 목적으로 사용되었으나, 최근에는 배치 정규화(Batch Normalization)가 더 흔하게 사용됩니다.
- 데이터 증강 (Data Augmentation):
- AlexNet은 데이터 증강 기법을 적극적으로 사용했습니다.
- 데이터 증강은 이미지를 변형시켜 학습 데이터셋을 다양하게 만드는 것을 의미합니다.
- 이를 통해 모델이 다양한 변형에 대해 더 강인하게 학습할 수 있습니다.
- 드롭아웃 (Dropout):
- AlexNet은 드롭아웃 기법을 사용하여 과적합을 줄였습니다.
- 드롭아웃은 학습 중에 무작위로 일부 뉴런을 비활성화시켜 일반화 성능을 향상시킵니다.
- AlexNet에서는 드롭아웃 비율을 0.5로 설정했습니다.
- 배치 크기 (Batch Size):
- AlexNet은 배치 크기를 128로 설정하여 학습을 수행했습니다.
- 배치 크기는 한 번의 업데이트에서 사용되는 샘플의 개수를 의미합니다.
- SGD Momentum:
- AlexNet은 SGD (Stochastic Gradient Descent) 최적화 방법을 사용했습니다.
- Momentum은 SGD에 적용되는 기법 중 하나로, 이전 그래디언트의 일부를 현재 업데이트에 반영하여 학습 속도를 향상시킵니다.
- AlexNet에서는 Momentum 값을 0.9로 설정했습니다.
- 학습률 (Learning Rate):
- AlexNet은 학습률을 초기에 0.01로 설정했으며, 검증 정확도가 더 이상 개선되지 않을 때 10으로 나누어 학습률을 감소시켰습니다.
- 이는 학습 과정에서 학습률을 조절하여 최적의 성능을 얻기 위한 전략입니다.
- L2 가중치 감쇠 (L2 Weight Decay):
- AlexNet은 L2 가중치 감쇠를 사용하여 모델의 복잡성을 제어했습니다.
- L2 가중치 감쇠는 가중치 값이 큰 경우에 페널티를 부과하여 일반화 성능을 향상시킵니다.
- 7개의 CNN 앙상블:
- 성능 향상을 위해 AlexNet은 7개의 CNN 모델을 앙상블하여 사용했습니다.
- 앙상블은 여러 모델의 예측을 결합하여 더 좋은 예측을 만들어내는 방법입니다.
- AlexNet의 앙상블은 오류율을 18.2%에서 15.4%로 낮추었습니다.
ZFNet
ZFNet은 2013년에 Matthew D. Zeiler와 Rob Fergus에 의해 제안된 딥러닝 모델로 AlexNet 모델을 기반으로 개선된 구조를 가지고 있다.
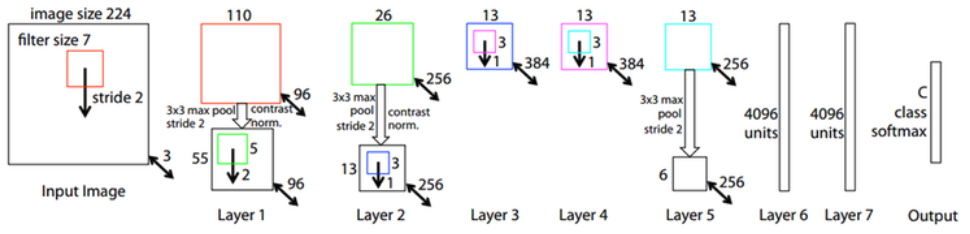
다음은 ZFNet의 주요 특징과 개선된 구성 요소에 대한 설명이다:
- 합성곱 계층(Convolutional Layers):
- ZFNet은 AlexNet과 마찬가지로 여러 개의 합성곱 계층을 포함하고 있습니다.
- 그러나 ZFNet에서는 AlexNet에 비해 더 큰 필터 크기와 작은 스트라이드(stride)를 사용하여 공간적인 정보를 더 잘 보존합니다.
- 이로 인해 더 세부적인 특징을 추출할 수 있습니다.
- 활성화 함수(Activation Function):
- ZFNet에서는 AlexNet에서 사용된 ReLU(Rectified Linear Unit) 활성화 함수를 그대로 사용합니다.
- ReLU는 비선형성을 도입하여 모델의 표현 능력을 향상시키는 데 도움을 줍니다.
- 최대 풀링 계층(Max Pooling Layers):
- ZFNet은 AlexNet과 유사하게 최대 풀링 계층을 사용하여 공간적인 크기를 줄입니다.
- 최대 풀링은 입력 영역에서 가장 큰 값을 선택하여 출력합니다.
- 완전 연결 계층(Fully Connected Layers):
- ZFNet은 AlexNet과 동일하게 완전 연결 계층을 사용하여 특징에 기반한 분류를 수행합니다.
- 여러 개의 뉴런으로 구성되어 있으며, 클래스 예측을 위해 소프트맥스 활성화 함수를 사용합니다.
- 가중치 초기화(Weight Initialization):
- ZFNet은 가중치 초기화에 대해 주의를 기울였습니다.
- 모델의 가중치를 초기화할 때 작은 값을 사용하여 학습 초기에 그래디언트가 크게 튀지 않도록 조절합니다.
ZFNet은 AlexNet과 유사한 구조를 가지고 있지만, 더 큰 필터 크기와 작은 스트라이드 등을 사용하여 공간적인 정보를 더욱 잘 보존하고 세부적인 특징을 추출할 수 있습니다. 이러한 개선된 구조와 가중치 초기화 전략은 ImageNet과 같은 대규모 데이터셋에서 좋은 성능을 보였다.
AlexNet과의 차이점은 더보기와 같다.
- CONV1 변경:
- AlexNet의 첫 번째 합성곱 계층(CONV1)의 설정을 변경하였습니다.
- AlexNet에서는 11x11 필터 크기와 4의 스트라이드를 사용했지만, 변경된 ZFNet에서는 7x7 필터 크기와 2의 스트라이드를 사용합니다.
- 이로 인해 입력 이미지의 공간적인 정보를 더 잘 보존하며, 더 작은 스트라이드로 인해 더 많은 픽셀을 커버할 수 있습니다.
- CONV3, CONV4, CONV5 변경:
- AlexNet의 세 번째, 네 번째, 다섯 번째 합성곱 계층(CONV3, CONV4, CONV5)의 필터 수를 변경하였습니다.
- AlexNet에서는 각각 384, 384, 256개의 필터를 사용했지만, ZFNet에서는 512, 1024, 512개의 필터를 사용합니다.
- 이로 인해 더 많은 특징을 추출할 수 있으며, 더 복잡한 이미지 패턴을 처리할 수 있습니다.
- ImageNet 상위 5개 오류:
- ZFNet의 변경된 구조와 설정을 통해 ImageNet 데이터셋에서의 성능 향상이 나타났습니다.
- AlexNet은 상위 5개 예측의 오류율이 16.4%였으나, 변경된 ZFNet에서는 11.7%로 상당한 성능 개선이 이루어졌습니다.
- 이는 더 깊고 정교한 구조, 변경된 필터 수, 그리고 다른 설정들이 인식 성능을 향상시켰음을 나타냅니다.
이제는 더 Deeper Networks을 사용하는 모델들을 살펴볼 것이다. 이전 AlexNet과 Znet은 8 layer만 사용했다. 이제부터 볼 VGG, GoogleNet은 19, 22개 ResNet은 152 layer를 사용한다.
VGG
VGG는
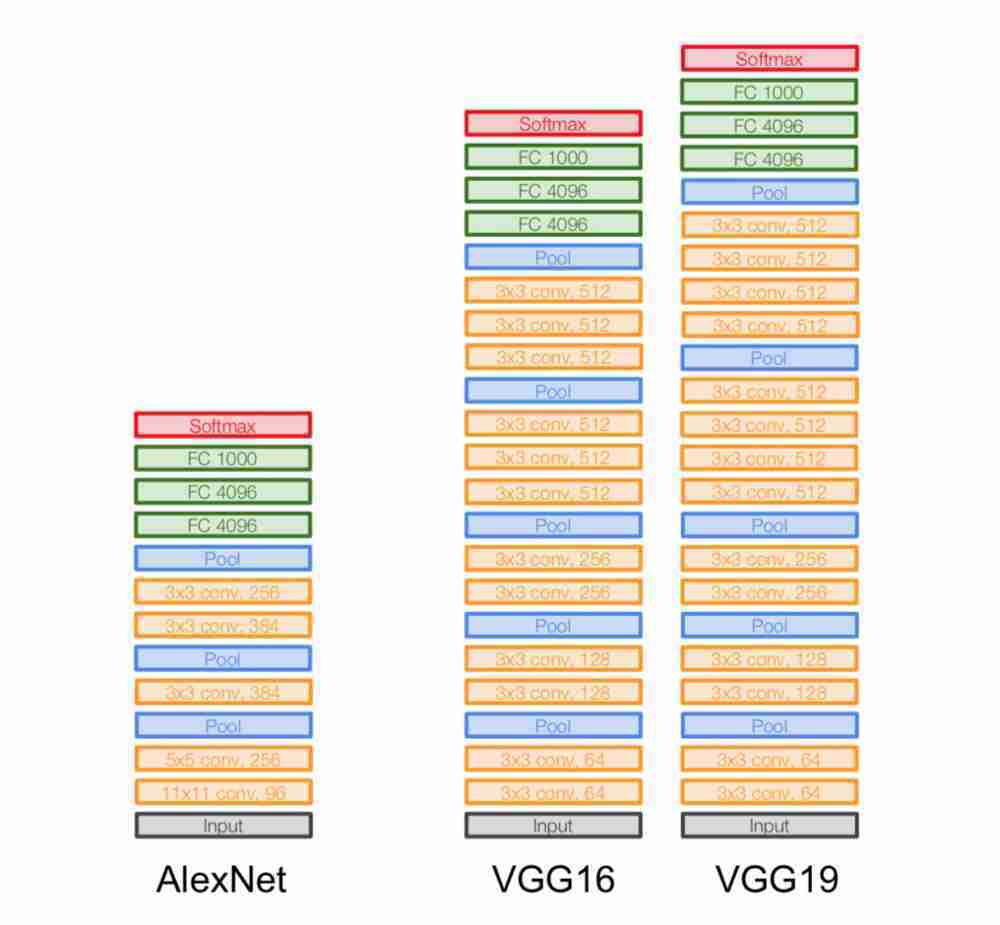
VGGNet은 2014년에 Karen Simonyan과 Andrew Zisserman에 의해 개발된 딥러닝 모델이다.
다음은 VGGNet의 주요 특징과 구성 요소에 대한 설명이다:
- 깊은 신경망 구조 (Deep Neural Network Architecture):
- VGGNet은 깊은 구조를 가지고 있으며, 총 16개 또는 19개의 계층으로 구성될 수 있습니다.
- 합성곱 계층(Convolutional Layer)과 완전 연결 계층(Fully Connected Layer)으로 구성되어 있습니다.
- 작은 필터 크기:
- VGGNet은 작은 3x3 크기의 필터를 사용하여 합성곱 계층을 구성합니다.
- 이 작은 필터 크기를 사용함으로써 더 많은 비선형성을 도입하고, 깊은 구조를 효과적으로 구성할 수 있습니다.
- 최대 풀링 계층 (Max Pooling Layers):
- VGGNet은 최대 풀링 계층을 사용하여 공간적인 크기를 줄입니다.
- 주로 2x2 크기의 필터와 2의 스트라이드를 사용하여 입력의 공간적인 크기를 반으로 줄입니다.
- 완전 연결 계층 (Fully Connected Layers):
- VGGNet의 마지막에는 완전 연결 계층이 있으며, 이미지 분류를 수행합니다.
- 이 계층은 추출된 특징에 기반하여 입력 이미지를 다양한 클래스로 분류합니다.
- 다양한 구조 (VGG16, VGG19):
- VGGNet은 VGG16과 VGG19의 두 가지 주요 변형으로 알려져 있습니다.
- VGG16은 16개의 계층으로 구성되어 있고, VGG19는 19개의 계층으로 구성되어 있습니다.
- 계층의 깊이에 따라 모델의 복잡성과 성능이 달라집니다.
그러면 VGG는 무엇이 중요한가. Params를 기본적으로 엄청나게 늘려138M parameter를 사용한다.
그렇다면 이게 어떻게 가능할까? 작은 필터의 사용 (3x3 합성곱)을 사용했기 때문이다.
- 작은 필터의 사용 (3x3 합성곱):
- VGGNet에서는 작은 3x3 크기의 필터를 사용하여 합성곱 계층을 구성합니다.
- 세 개의 3x3 필터 계층을 쌓은 경우와 하나의 7x7 필터 계층을 사용한 경우와 동일한 효과적인 수용 영역(effective receptive field)을 가집니다.
- 작은 필터를 쌓으면 더 깊은 네트워크와 더 많은 비선형성을 도입할 수 있습니다.
- 또한, 매개 변수의 수가 줄어들기 때문에 효율적인 모델 구성이 가능합니다.

위의 5x5 conv을 다음과 같이 3x3 필터를 적용해 stride(컨볼루션 연산에서 필터가 입력 데이터를 이동하는 간격을 의미) 1을 적용하면 다음과 그림과 같이 변한다.

즉, 더 많은 비선형성을 도입하고, 깊은 구조를 효과적으로 구성할 수 있다. 더 많은 정보를 필요로한다면 다음의 블로그를 참조하면 좋다.
[VGGNet] VGGNet 개념 정리
안녕하세요 대추입니다. 이번에 딥러닝에 대해 공부를 하며 VGGNet도 건드려 봤는데 사용하기전 알아두면 좋을 만한 것에 대해 정리해보고자 작성하게 되었습니다. VGGNet에는 A, A-LRN, B, C, D, E가 있
daechu.tistory.com
GoogLeNet
GoogLeNet은 2014년에 Google Research에서 개발된 딥러닝 모델로, "Inception" 아키텍처라고도 알려져 있다.

다음은 GoogLeNet의 주요 특징과 구성 요소에 대한 설명이다:
- 인셉션 모듈 (Inception Module):
- GoogLeNet은 인셉션 모듈을 사용하여 네트워크를 구성합니다.
- 인셉션 모듈은 다양한 필터 크기의 합성곱 계층을 동시에 수행하고, 이를 병렬로 연결하여 다양한 크기의 특징을 추출합니다.
- 이를 통해 네트워크의 표현 능력을 향상시키고, 계산량을 효과적으로 줄일 수 있습니다.
- 1x1 합성곱 (1x1 Convolution):
- GoogLeNet은 1x1 크기의 합성곱 연산을 적극적으로 활용합니다.
- 1x1 합성곱은 채널 간의 선형 결합을 통해 차원 축소를 수행합니다.
- 이를 통해 계산량을 감소시키고, 모델의 복잡성을 제어합니다.
- 네트워크 구조의 깊이와 너비:
- GoogLeNet은 깊고 넓은 네트워크 구조를 가지고 있습니다.
- 총 22개의 계층으로 구성되어 있으며, 이 중에서도 인셉션 모듈이 주요 구성 요소입니다.
- 네트워크의 깊이와 너비를 조정하여 다양한 크기의 특징을 포착하고 복잡한 패턴을 학습할 수 있습니다.
- Auxillary 분류기 (Auxiliary Classifiers):
- GoogLeNet은 중간에 Auxillary 분류기를 포함하고 있습니다.
- 이 분류기는 네트워크의 중간 단계에서 손실을 계산하여 역전파를 돕습니다.
- 이를 통해 그래디언트 신호가 초기 계층으로 전달되어 기울기 소실을 완화하고 학습을 안정화시킵니다.
Inception module
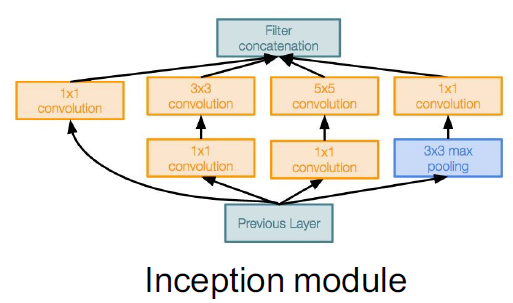
Inception 모듈은 좋은 지역 네트워크 토폴로지(지역적인 작은 네트워크의 구성)를 설계한다. 이 지역 네트워크는 서로 다른 크기의 필터를 사용하여 병렬로 연산을 수행하며, 다양한 필터 크기를 사용함으로써, 모델은 다양한 크기의 특징을 동시에 추출할 수 있다. 이는 네트워크의 표현 능력을 향상시키는 데 도움을 준다.
GoogleNet은 Inception 모듈들을 서로 쌓아 올림으로써, 전체 네트워크를 구성한다. 쌓인 Inception 모듈은 네트워크의 깊이를 증가시키고, 더 복잡한 패턴을 학습할 수 있도록 한다. 이렇게 설계된 Inception 모듈은 GoogLeNet의 핵심 구성 요소이며, 이미지 인식 작업에서 뛰어난 성능을 보이는 데 일조한다.
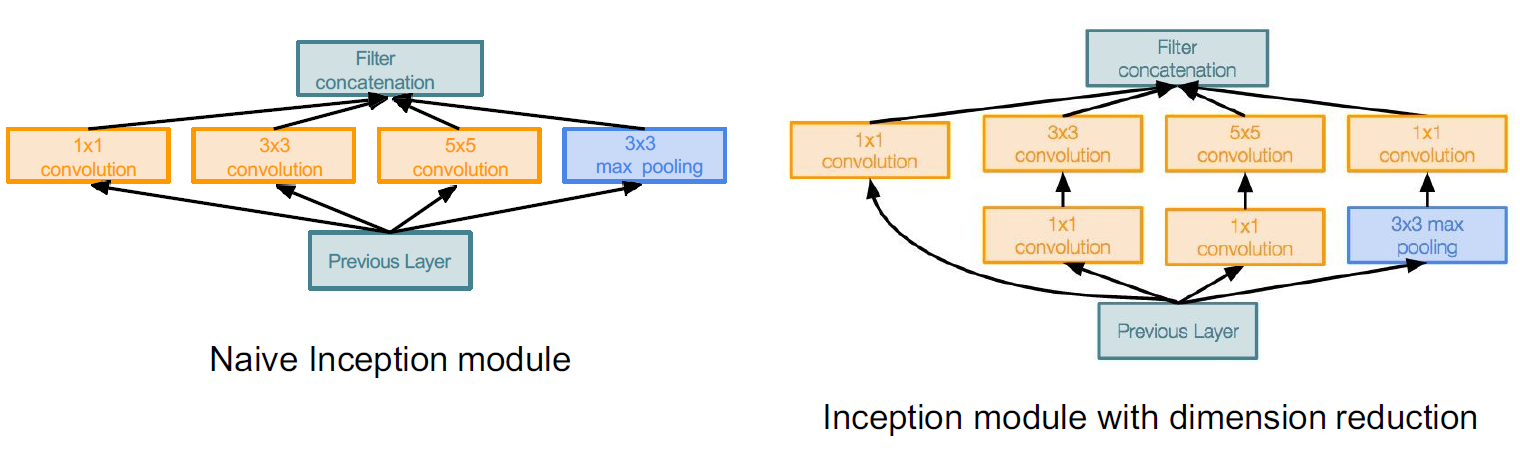
Naive Inception 모듈과 Inception module with dimension reduction은 Inception 네트워크의 구성 요소로서 차이가 있습니다.
- Naive Inception 모듈:
- Naive Inception 모듈은 각각 다른 필터 크기의 합성곱 연산을 수행하여 병렬로 연결됩니다.
- 예를 들어, 1x1, 3x3, 5x5 크기의 필터를 사용한 합성곱이 동시에 이루어집니다.
- 각각의 필터 크기마다 합성곱을 수행하고, 그 결과를 채널 방향으로 결합합니다.
- Inception 모듈 with dimension reduction:
- Inception 모듈 with dimension reduction은 입력 데이터의 채널 수를 줄이기 위해 1x1 합성곱을 사용합니다.
- 이러한 1x1 합성곱은 채널 간의 선형 결합을 통해 차원 축소를 수행합니다.
- 1x1 합성곱은 필터 크기를 줄이고 채널 수를 감소시키는 역할을 합니다.
- 이후에는 작은 필터 크기(예: 3x3, 5x5)를 사용한 병렬 합성곱이 수행됩니다.
따라서, Naive Inception 모듈은 각 필터 크기에 대한 병렬 합성곱만 수행하지만, Inception 모듈 with dimension reduction은 1x1 합성곱을 사용하여 차원 축소를 수행한 후에 병렬 합성곱을 수행한다. 이를 통해 Inception 모듈 with dimension reduction은 모델의 복잡성을 조절하면서도 효율적인 특징 추출을 가능하게 한다.
말로써는 이해하기 쉽지 않으니 그림을 통해 이해해보자.
Naive Inception
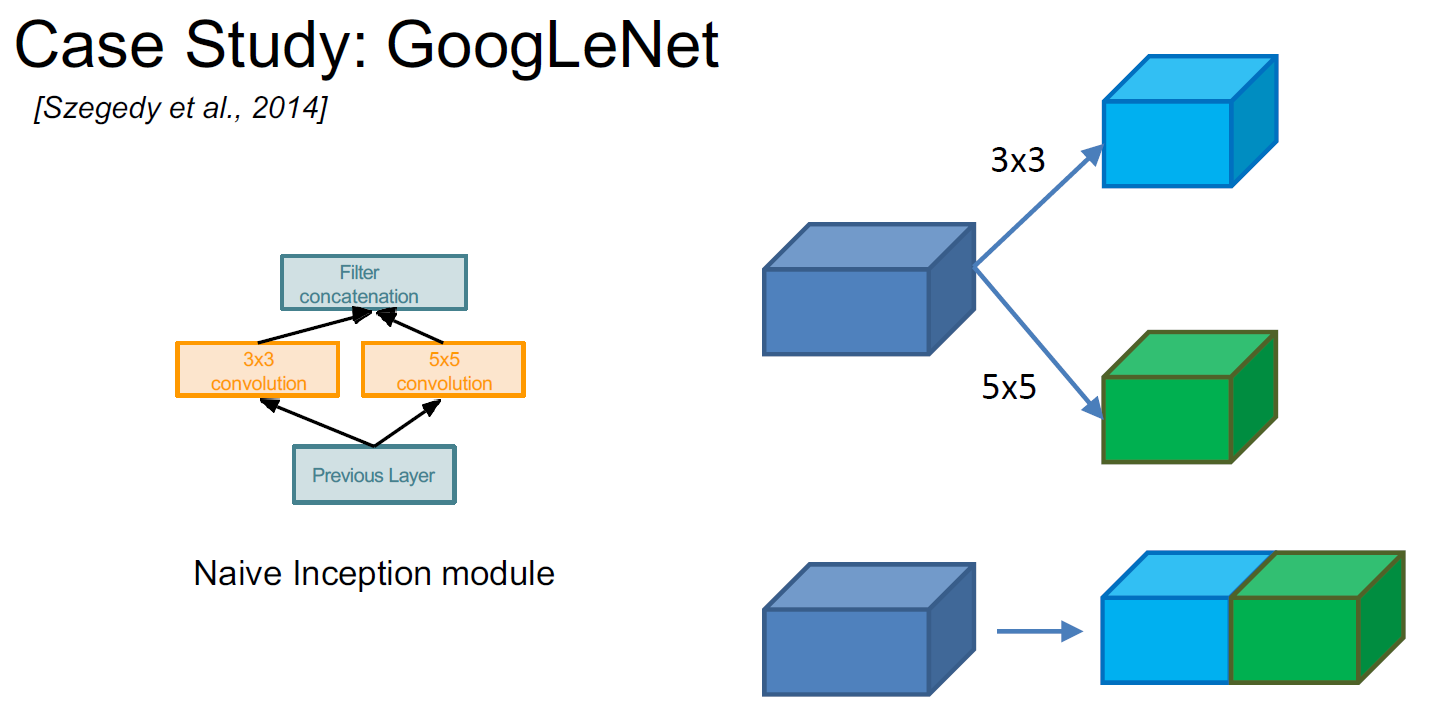
Naive Inception은 각각의 합성곱을 연산 후, 이어 붙인다고 생각하면 된다.
Inception module with dimension reduction
이걸 이해하려면 1 X 1 convolution을 이해해야된다.
1x1 합성곱은 다음과 같은 특징을 갖는다:
- 차원 축소(Dimension Reduction):
- 1x1 합성곱은 입력 데이터의 채널 수를 줄이는 역할을 합니다.
- 채널 수를 감소시키면 모델의 복잡성을 줄이고, 계산 비용을 절감할 수 있습니다.
- 비선형 연산:
- 1x1 합성곱은 비선형 활성화 함수를 적용합니다.
- 이를 통해 모델은 비선형성을 도입하고, 더 복잡한 특징을 추출할 수 있습니다.
- 특성 맵 결합:
- 1x1 합성곱은 여러 개의 1x1 필터를 사용하여 다양한 특성 맵을 동시에 계산할 수 있습니다.
- 이를 통해 모델은 다양한 특징을 동시에 학습하고, 다양한 정보를 포착할 수 있습니다.
- 파라미터 수 감소:
- 1x1 합성곱은 작은 필터 크기를 사용하므로 학습해야 할 파라미터 수가 크게 줄어듭니다.
- 이를 통해 모델의 메모리 요구사항을 줄이고, 학습 및 추론 속도를 향상시킬 수 있습니다.
1x1 합성곱은 네트워크에서 다양한 목적으로 사용된다. 가장 일반적인 용도는 차원 축소와 병렬 계산을 위한 특성 맵의 결합입니다. 이를 통해 모델의 성능과 효율성을 향상시킬 수 있다.
글만으로는 햇갈리니 그림을 통해 이해해보자.
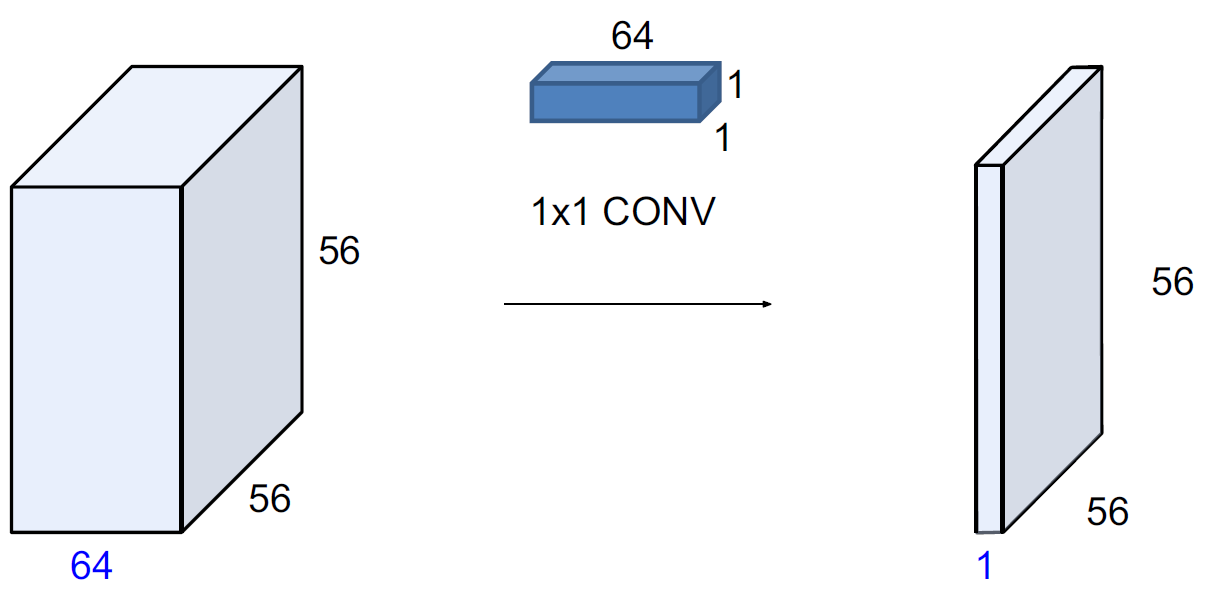
64x1x1 필터를 사용해서 64x56x56를 1x56x56으로 변환할 수 있다는 말이다. 즉, 우리가 원하는 형태로 1x1 합성곱은 공간적인 차원을 보존하면서도 깊이를 줄이며, 낮은 차원으로 깊이를 투영한다. 다음과 같은 형태로 말이다.
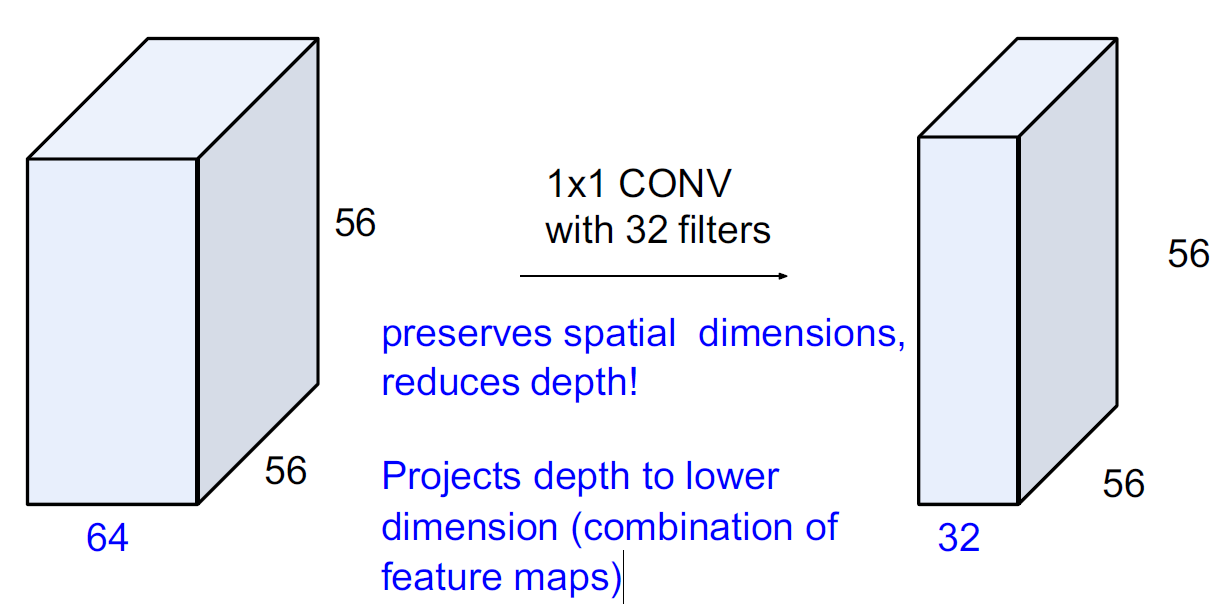
그래서 GoogLeNet에서는 다음과 같이 파라미터를 줄였다.

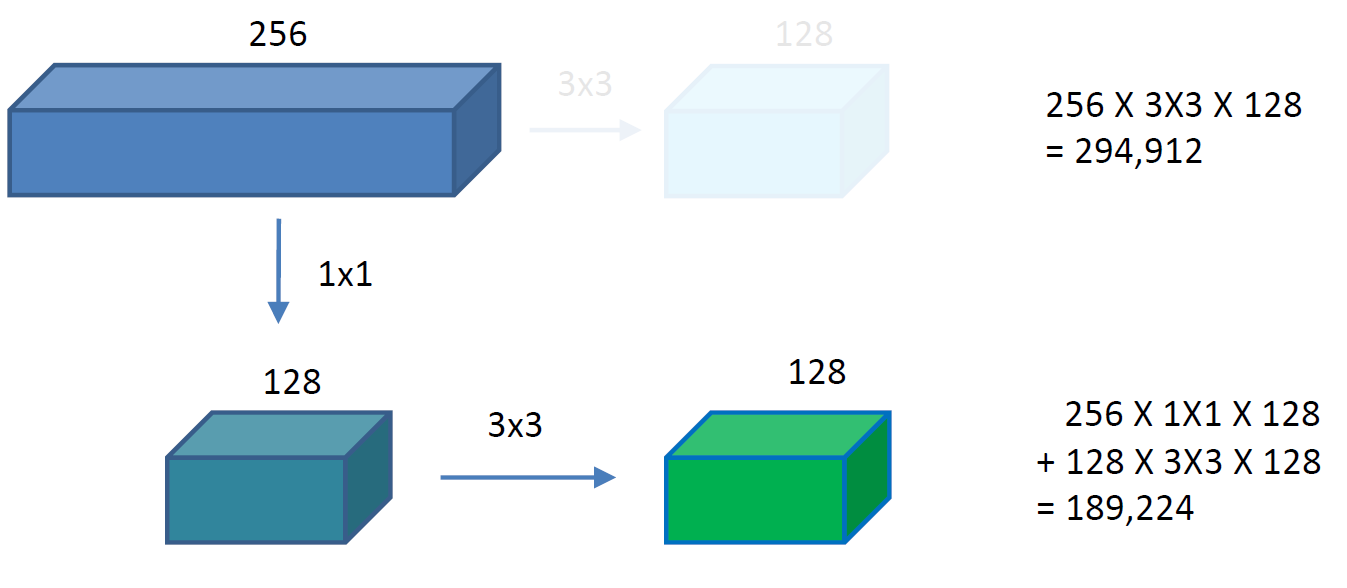
추가적으로 3x3 max pooling을 1x1 conolution이전에 실행하여 향상된 기능 맵(Enhanced feature map)을 만들어서 사용한다. (특성을 최대한 잃지 않기 위해서)

왜 이런일을 하냐고하면 결국 computing할 parameter를 줄이기위한것이다.
Auxiliary classification outputs to inject additional gradient at lower layers는 이전에 설명했으니 위치만 알면 될 듯하다.
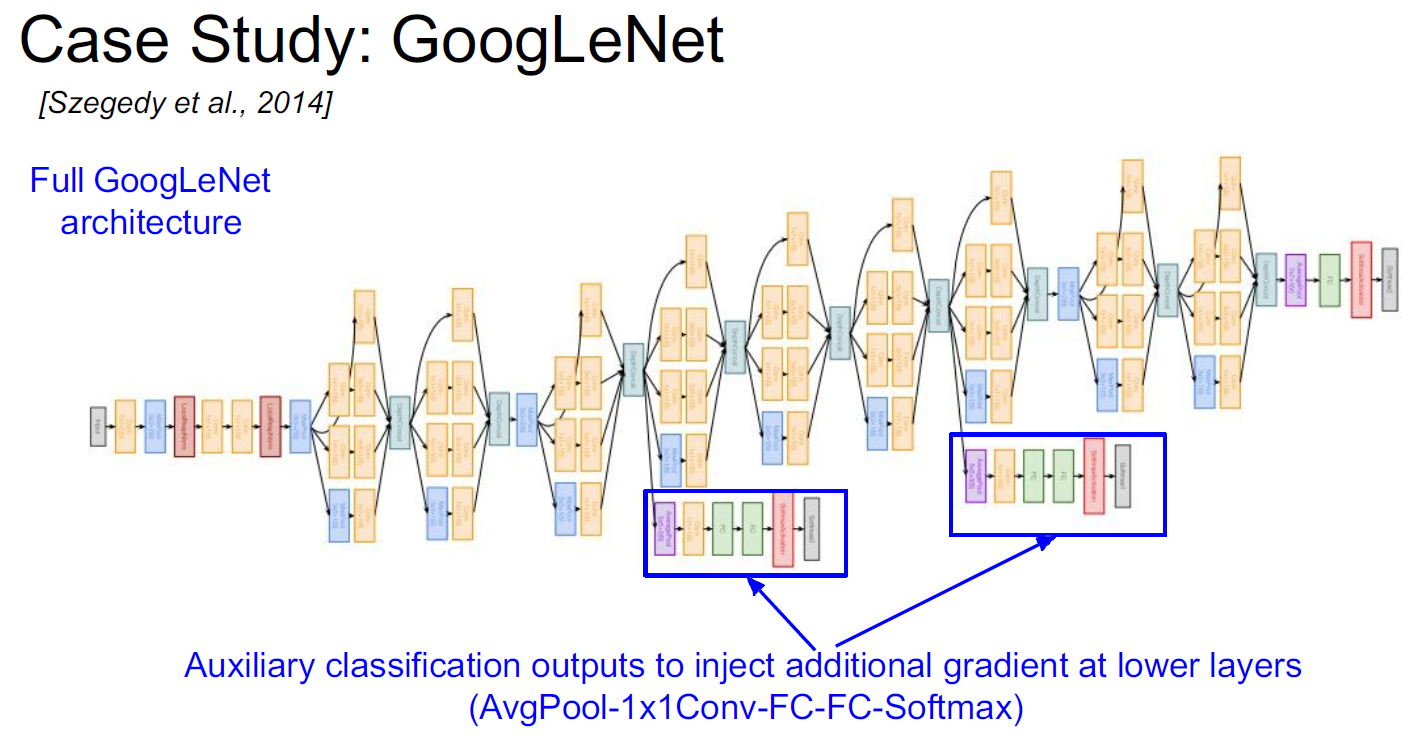
즉, GoogLeNet은 깊고 넓은 구조, 인셉션 모듈, 1x1 합성곱, Auxillary 분류기 등의 특징을 통해 이미지 인식 분야에서 높은 성능을 보이는 모델이다. 이러한 아키텍처는 모델의 표현 능력을 향상시키고, 계산 효율성을 유지하며, 기울기 소실 문제를 완화함으로써 학습을 개선했다.
더 많은 정보를 참조하려면 다음의 블로그를 참조하면 좋다.
[CNN 알고리즘들] GoogLeNet(inception v1)의 구조
LeNet-5 => https://bskyvision.com/418 AlexNet => https://bskyvision.com/421 VGG-F, VGG-M, VGG-S => https://bskyvision.com/420 VGG-16, VGG-19 => https://bskyvision.com/504 GoogLeNet(inception v1) => https://bskyvision.com/539 ResNet => https://bskyvision.co
bskyvision.com
ResNet
ResNet은 152개의 layer를 사용한 Revolution of Depth를 보여주었다.
"평범한" 합성곱 신경망에 더 깊은 계층을 계속 쌓으면 어떤 일이 벌어질까?

56 계층 모델은 학습 및 테스트 오류 모두에서 성능이 저하된다.
-> 더 깊은 모델은 성능이 저하되지만, 이는 과적합으로 인한 것이 아니다
보통의 합성곱 신경망에 더 깊은 계층을 추가하면 모델의 성능이 저하될 수 있습니다. 이는 더 깊은 모델이 과적합으로 인해 성능이 저하되는 것이 아니라는 것을 의미합니다. 즉, 더 깊은 신경망은 훈련 및 테스트 오류 모두에서 성능이 악화됩니다.
더 깊은 모델에서의 성능 저하는 그래디언트 소실이나 폭주와 같은 문제와 관련이 있을 수 있습니다. 네트워크가 깊어짐에 따라 그래디언트가 전파되는 것이 어려워지고, 정보가 손실될 수 있습니다. 이로 인해 모델이 제대로 학습되지 않아 성능이 저하될 수 있습니다.
따라서, "평범한" 합성곱 신경망에 계층을 추가할 때는 그저 더 깊은 모델을 만들어서 성능이 향상될 것으로 기대하는 것은 적절하지 않습니다. 대신에, 그래디언트 소실이나 폭주 등의 문제를 완화하기 위해 적절한 해결책이 필요합니다. 이를 위해서는 ResNet과 같은 구조적인 개선이나 다른 기법들을 적용하여 깊은 신경망의 학습을 개선해야 합니다.
이를 해결하기 위해 Residual을 사용했다. Residual을 그림으로 살펴보자.

Residual을 사용하면 매우 깊은 네트워크 깊은 네트워크를 만들 수 있다. 이게 가능한 이유를 그림을 통해 알아보자.
일반적은 NN은 다음과 같이 작용할 것이다.
하지만 Residual은 다음과 같이 작동한다. 먼저, Y-X에 대한 값을 예측하는 NN을 만든다.

이를 보완하기 위해, Y-X 계산 후에 추가적으로 X를 더해 Y값을 얻어낸다.
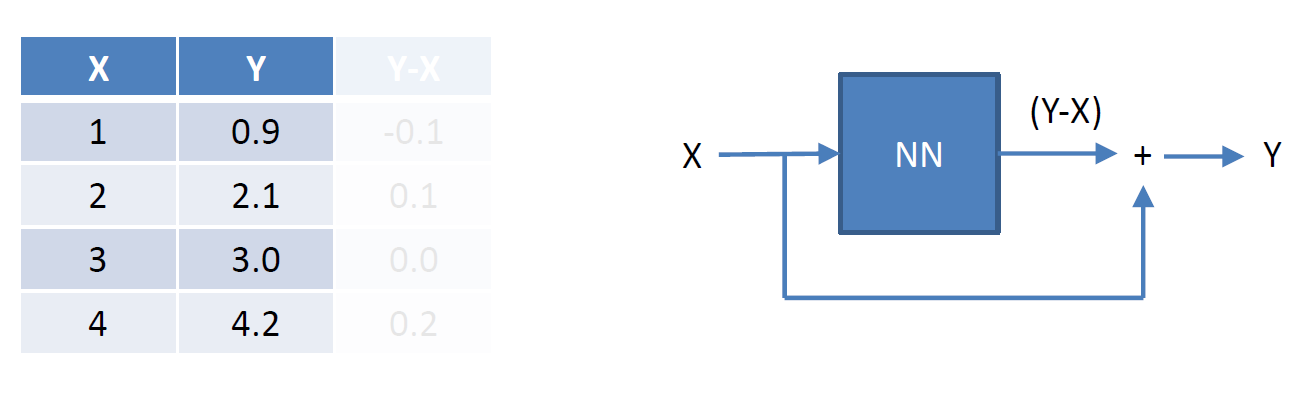
즉, 네트워크를 쌓는다면 다음과 같이 쌓일 것이다.
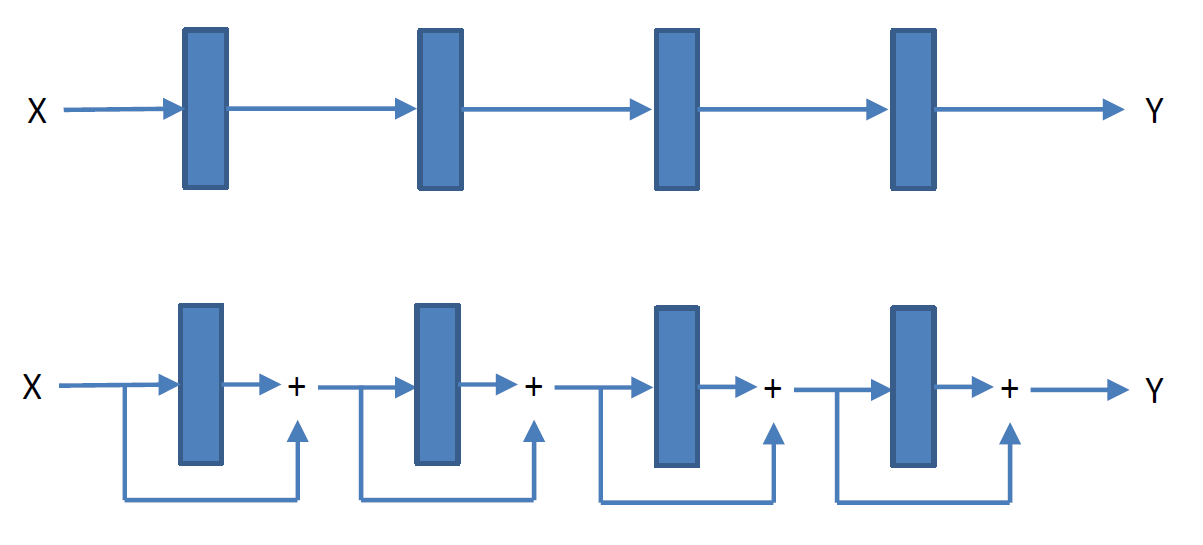
ResNet에서 사용된 방식은 다음과 같다.

ResNet은 다음과 같은 전체 아키텍처와 실제 훈련 방법을 가지고 있습니다:
- ResNet 아키텍처:
- 잔차 블록을 쌓습니다.
- 각 잔차 블록은 두 개의 3x3 크기의 합성곱 계층을 가지고 있습니다.
- 주기적으로 필터의 수를 두 배로 늘리고, 공간적으로 다운샘플링을 수행합니다. 이는 각 차원마다 stride 2 (/2)를 사용하여 공간 크기를 줄입니다.
- 시작 부분에 추가적인 합성곱 계층이 있습니다.
- 마지막에 FC (Fully Connected) 계층은 없으며, 출력 클래스에 대한 FC 1000 계층만 존재합니다.
- 마지막 합성곱 계층 이후에는 Global Average Pooling 계층이 적용됩니다.
- ResNet 훈련 방법:
- 각 합성곱 계층 뒤에 배치 정규화(Batch Normalization)가 적용됩니다.
- He et al.의 Xavier/2 초기화를 사용합니다.
- SGD + Momentum (0.9) 최적화 알고리즘을 사용합니다.
- 학습률은 0.1이며, 검증 오류가 더 이상 개선되지 않을 때 10으로 나눕니다.
- 미니 배치 크기는 256입니다.
- 가중치 감쇠(Weight decay)로 1e-5를 사용합니다.
- Dropout은 사용되지 않습니다.
이러한 방법으로 ResNet을 훈련시키면서 배치 정규화, 초기화, 최적화, 학습률 조절 등의 기법을 적용하여 네트워크를 효과적으로 학습시킬 수 있다.
추가적으로 ResNet을 정리하면 다음과 같다.
ResNet은 "Residual Network"의 줄임말로, 네트워크 깊이가 깊어질수록 발생하는 그래디언트 소실 문제를 해결하기 위한 구조적인 개선을 가지고 있다. 이러한 구조적인 개선은 네트워크의 깊이를 무제한으로 확장할 수 있는 장점을 가지며, 대규모 이미지 인식 작업에서 뛰어난 성능을 보인다.
다음은 ResNet의 주요 특징과 개선된 구성 요소에 대한 설명이다:
- 잔차 연결 (Residual Connection):
- ResNet은 잔차 연결을 도입하여 네트워크 깊이가 깊어질 때 발생하는 그래디언트 소실 문제를 해결합니다.
- 잔차 연결은 입력과 출력을 직접적으로 연결하여 중간 계층에서 발생한 잔차를 전파합니다.
- 이를 통해 기울기의 소실을 완화하고, 더 깊은 네트워크에서도 효과적인 학습을 가능하게 합니다.
- 합성곱 블록 (Convolutional Block):
- ResNet은 합성곱 블록이라고도 불리는 기본 구성 요소를 사용하여 네트워크를 구성합니다.
- 각 합성곱 블록은 여러 개의 합성곱 계층과 배치 정규화(Batch Normalization) 및 활성화 함수(ReLU) 등을 포함합니다.
- 이러한 합성곱 블록은 네트워크의 복잡성과 표현 능력을 조절하는 역할을 합니다.
- 스킵 연결 (Skip Connection):
- ResNet은 스킵 연결을 통해 정보의 바로 가기 경로를 만듭니다.
- 스킵 연결은 잔차 연결과 유사하지만, 더 짧은 경로를 사용하여 그래디언트 흐름을 보존합니다.
- 이를 통해 네트워크가 보다 원활하게 학습되며, 속도와 정확성을 동시에 향상시킵니다.
- 다양한 깊이의 ResNet:
- ResNet은 다양한 깊이의 모델을 제공합니다. 대표적으로 ResNet-18, ResNet-34, ResNet-50, ResNet-101, ResNet-152 등이 있습니다.
- 깊은 모델에서는 스킵 연결이 많이 사용되며, 네트워크의 깊이를 확장함에 따라 성능이 향상됩니다.
ResNet은 그래디언트 소실 문제를 극복하고 깊은 네트워크에서도 효과적인 학습을 가능하게 해주는 혁신적인 딥러닝 모델이다.
Densely Connected Convolutional Networks(DenseNet)
DenseNet은 2016년에 개발된 딥러닝 모델로, Kaiming He 등의 연구진에 의해 제안되었다. DenseNet은 네트워크의 각 계층이 이전 계층의 모든 출력과 연결되는 밀집 연결 구조를 가지고 있어 특징적인 특징을 가지고 있다. 이 구조는 그래디언트 흐름의 원활성과 효율적인 특징 재사용을 통해 네트워크의 성능과 학습 효율성을 향상시킨다.
DenseNet의 주요 특징과 구성 요소는 다음과 같다:
- 밀집 연결 (Dense Connections):
- DenseNet은 밀집 연결 구조를 사용하여 각 계층이 이전 계층의 모든 출력과 연결됩니다.
- 이러한 밀집 연결은 정보의 흐름을 최적화하고, 그래디언트를 보존하며, 특징 재사용을 촉진합니다.
- 각 계층은 이전 계층에서 생성된 특징 맵을 입력으로 받아들이며, 이를 연결하여 새로운 특징 맵을 생성합니다.
- 컴팩트한 구조:
- DenseNet은 비교적 적은 매개 변수를 가진 컴팩트한 구조를 가지고 있습니다.
- 밀집 연결로 인해 모든 계층이 이전 계층과 직접 연결되므로, 매개 변수의 수가 증가하지 않습니다.
- 이를 통해 모델의 복잡성을 조절하고, 메모리 요구사항과 계산 비용을 줄일 수 있습니다.
- 특징 재사용:
- 밀집 연결로 인해 이전 계층의 모든 출력이 현재 계층에 직접 전달되므로, 특징 재사용이 용이해집니다.
- 이는 모델이 훈련 데이터의 다양한 특징을 잘 학습하고, 작은 데이터셋에서도 효과적으로 일반화할 수 있도록 도와줍니다.
- 특징 병합:
- DenseNet은 각 밀집 블록에서 생성된 특징 맵을 병합(concatenate)하는 과정을 반복합니다.
- 이를 통해 네트워크는 다양한 수준의 추상화된 특징을 효과적으로 학습할 수 있습니다.
- 특징 병합은 모델이 풍부한 특징을 학습하고, 성능을 향상시키는 데 기여합니다.

DenseNet은 네트워크가 커지더라도 그래디언트 소실 문제를 해결하고 특징 재사용을 통해 성능을 향상시킬 수 있는 강력한 구조를 제공합니다.
- 각 계층이 순전파 방식으로 모든 다른 계층과 연결된 DenseNet에서의 Dense 블록은 다음과 같은 역할을 합니다:
- 그래디언트 소실 문제 완화: Dense 블록에서는 각 계층이 다른 모든 계층과 연결되므로, 그래디언트가 빠르게 전파되어 그래디언트 소실 문제를 완화시킵니다. 이는 깊은 신경망에서 그래디언트가 사라지는 것을 방지하고, 훈련 과정에서 더 효과적으로 가중치를 업데이트할 수 있게 도와줍니다.
- 특징 전파 강화: Dense 블록에서의 밀집한 연결 구조는 특징의 전파를 강화시킵니다. 각 계층은 모든 다른 계층과 직접적으로 연결되어 정보가 자유롭게 흐를 수 있게 합니다. 이는 네트워크의 표현 능력을 향상시키고, 각 계층이 공헌할 수 있는 특징을 최대한 활용할 수 있게 합니다.
- 특징 재사용 장려: Dense 블록에서는 각 계층이 다른 모든 계층과 연결되므로, 이전 계층에서 추출한 특징을 현재 계층에서 재사용할 수 있습니다. 이는 모델이 훈련 데이터의 다양한 특징을 잘 학습하고, 작은 데이터셋에서도 효과적으로 일반화할 수 있도록 도와줍니다.
- DenseNet의 Dense 블록은 그래디언트 소실 문제를 완화하고 특징 전파를 강화시키며, 특징 재사용을 장려하여 모델의 성능과 학습 효율성을 향상시킵니다. 이는 DenseNet이 다양한 컴퓨터 비전 작업에서 뛰어난 성능을 보이는 데 도움을 줍니다.
Summary: CNN Architectures
- VGG, GoogLeNet, ResNet 모두 널리 사용
- ResNet 현재 최상의 기본값
- 극도로 깊은 네트워크로의 트랜드
- 레이어/스킵 연결 설계 및 기울기 흐름 개선에 관한 중요한 연구 센터
- 깊이 대 너비 및 잔여 연결의 필요성을 검토하는 훨씬 더 최근의 추세
Depthwise Separable Convolution
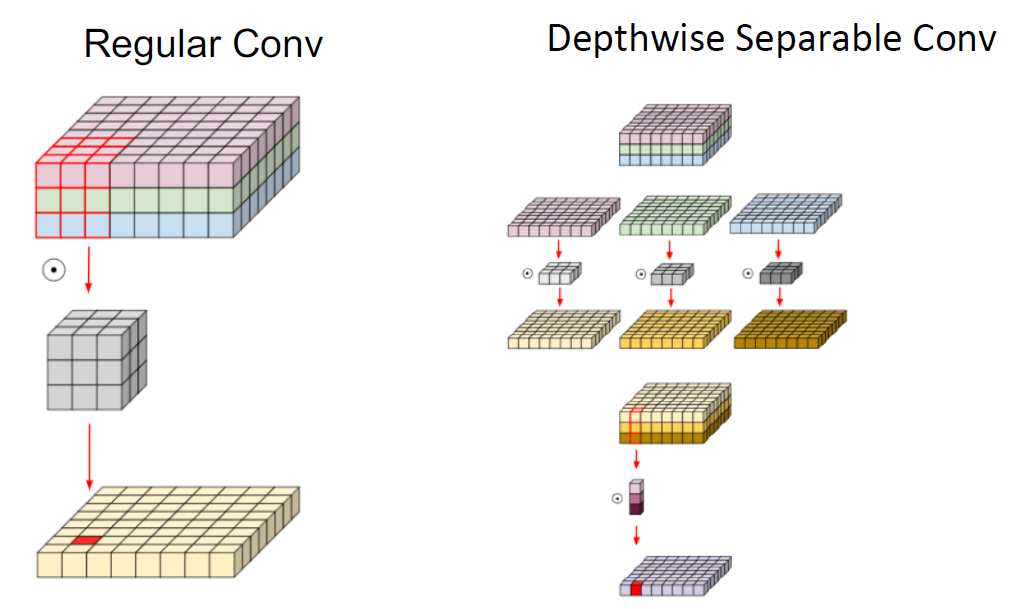
epthwise Separable Convolution은 컨볼루션 연산의 효율성을 높이기 위한 기법 중 하나입니다. 기존의 컨볼루션 연산은 입력 채널과 필터 사이의 모든 위치에서 독립적으로 계산을 수행합니다. 이에 비해 Depthwise Separable Convolution은 컨볼루션 연산을 두 단계로 나누어 수행하여 계산 비용을 줄입니다.
Depthwise Separable Convolution은 다음과 같은 단계로 이루어집니다:
- Depthwise Convolution:
- 입력 채널별로 필터를 적용하여 각 입력 채널에서 특징 맵을 독립적으로 계산합니다.
- 각 입력 채널에 대해 하나의 작은 필터를 사용하여 입력 채널별로 채널별 컨볼루션 연산을 수행합니다.
- 이 과정은 입력 채널 수에 따라 채널별 컨볼루션 연산을 병렬로 수행합니다.
- Pointwise Convolution:
- Depthwise Convolution의 결과로 나온 특징 맵에 1x1 크기의 필터를 사용하여 채널 간의 선형 결합을 수행합니다.
- 이는 각 채널의 특징 맵을 조합하여 최종 출력 특징 맵을 생성합니다.
- 즉, 채널 간의 관계를 학습하고, 공간 방향의 정보를 인코딩하는 역할을 합니다.
Depthwise Separable Convolution은 기존의 컨볼루션에 비해 매개 변수 수와 계산 비용을 크게 줄여준다. Depthwise Convolution에서는 입력 채널별로 필터를 공유하기 때문에 매개 변수 수가 감소하고, Pointwise Convolution에서는 채널 간의 선형 결합을 통해 필터 크기가 작아지기 때문에 계산 비용이 감소한다. 이를 통해 모델의 효율성과 경량화를 달성할 수 있다. Depthwise Separable Convolution은 모바일 장치와 같은 계산 자원이 제한된 환경에서 특히 유용하며, 작은 모델 크기와 빠른 추론 속도를 제공한다.
그림으로 이해하면 편하다.
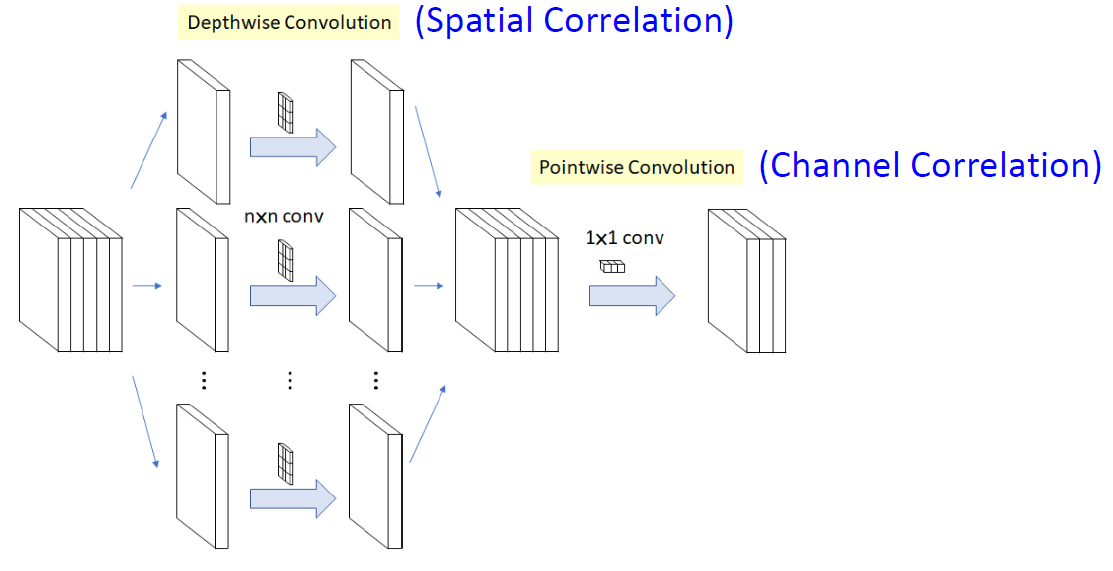
나머지는 참조하면 좋은 것들이다.

'인공지능' 카테고리의 다른 글
| Chapter 6 Transformer Model (0) | 2023.05.20 |
|---|---|
| Chapter 5 RNN, LSTM, GRU (1) | 2023.05.19 |
| Diffusion Model (0) | 2023.04.01 |
| Chapter 3 Convolutional Neural Networks (0) | 2023.02.13 |
| Chapter 2-2 Neural Networks (0) | 2023.02.05 |



