Ashish Vaswani, Noam Shazeer , Niki Parmar, Jakob Uszkoreit , Llion Jones, Aidan N. Gomez, Łukasz Kaiser, Illia Polosukhin , "Attention Is All You Need," NIPS 2018를 바탕으로 작성되었다.
우리는 Chapter 5에서 Attention model을 통해 Sequential computation 사용하여 병렬화를 방지했다. 하지만 GRU 및 LSTM에도 불구하고 RNN은 여전히 장거리 종속성을 처리하기 위한 attention mechanism이 필요하다.
이전을 살펴보면 다음과 같다.

이를 실제로 사용하면 생각보다 잘 되지 않는다는 것을 알 수 있다.
일단 이를 해결해보기 위해 attention mechanism을 나이브하게 보자.

이는 결국 다음과 같이 하나의 module로 보일 것이다.

결국 진행되다보면 다음과 같아질 것이다.

즉, 다음과 같게 볼 수 있다.

이런 인코더-디코더 접근법을 활용하여 Transformer가 탄생했다.
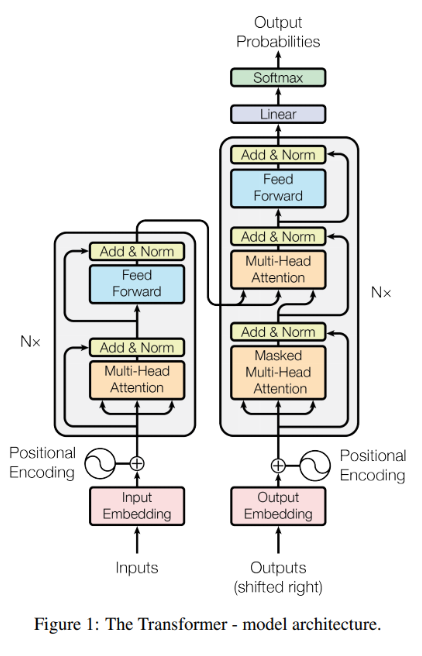
아래가 인코더 파트이다.

아래가 디코더 파트이다.

디코더는 후에 서술할 것이다.
인코더부터 살펴보자.
입력 문장에 단어를 삽입한 후 각 단어는 인코더의 두 계층을 통해 흐른다.
아래는 인코더를 더 간단하게 도식화시킨 것으로 Residual을 하나의 계층으로 보면 2개의 계층으로 나뉘는 것을 볼 수 있다.

이전의 Attention Mechanism을 생각해보자. 아래의 구조가 기억날 것이다.

이게 앞에서 많은 h를 거쳐왔다면 context(query)에 쌓여있을 것이고 이를 다음과 같이 표현할 수 있다.

식을 다시보면 이전의 어떤 식이 떠올라야한다. 그렇다 softmax다. 따라서 다음의 식으로 인지해야한다.

따라서 다음과 같은 형태로 인지할 수 있다.
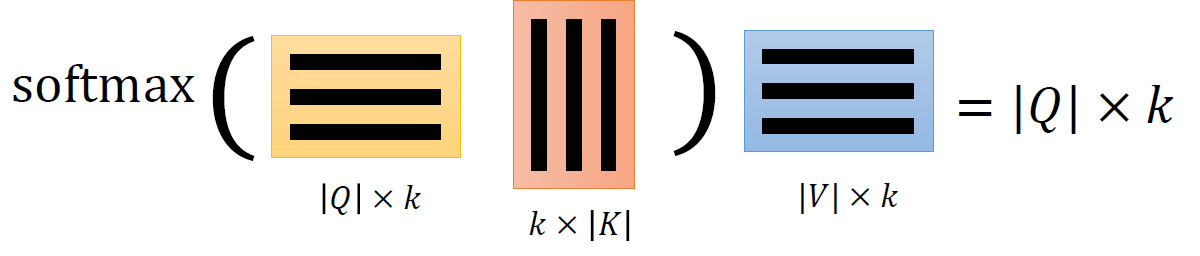
따라서 우리는 다음의 직관을 얻을 수 있다.
|𝑘|가 커짐에 따라, 𝑄𝐾𝑇의 분산은 증가한다.
→ 소프트맥스 내부의 일부 값들이 커진다
→ 소프트맥스는 매우 뾰족해진다
→ 그레디언트는 작아진다
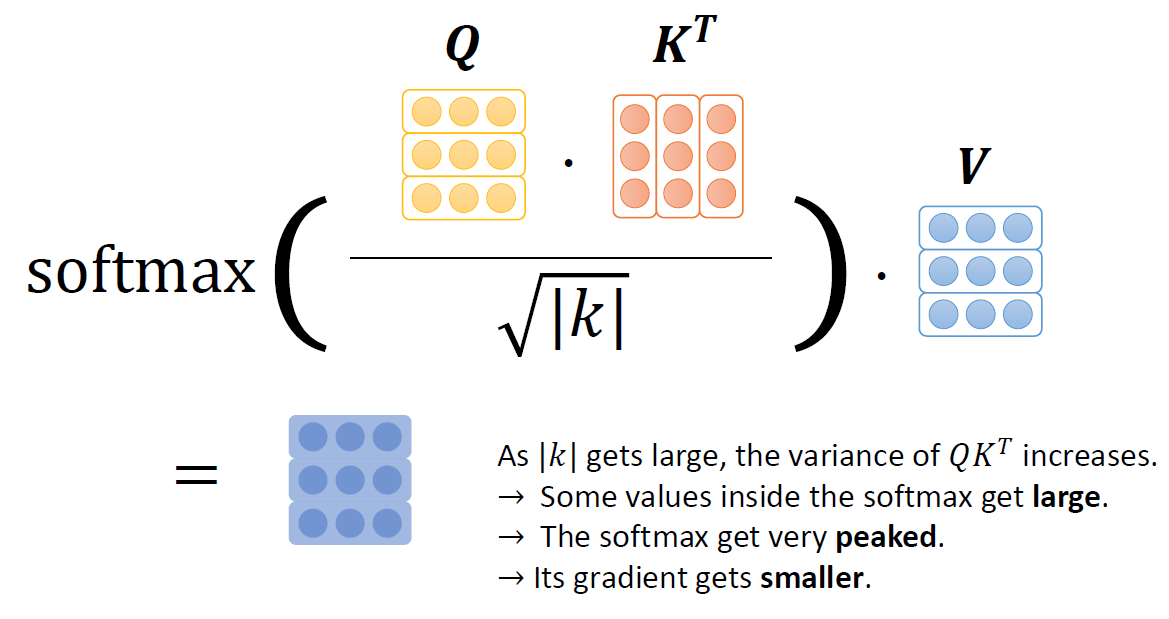
그래서 우리는 다음을 얻을 수 있다.
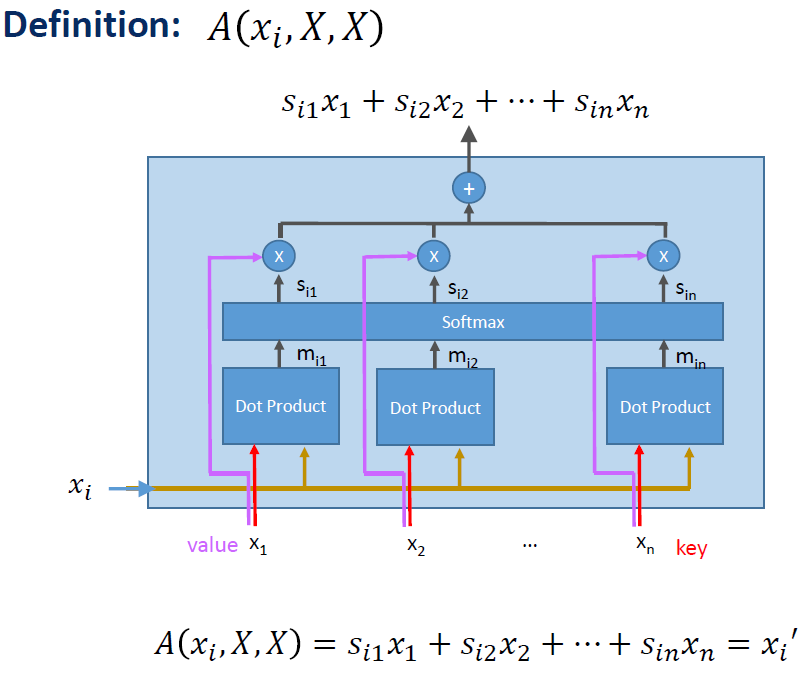
즉, 다음의 식을 얻는다는 것이다.

이를 Self-Attention이라고 부른다. 이는 네트워크에서 장거리 종속성 학습이 가능하며, 효율적인 계산을 위한 병렬화에 효과적이다.
아래와 같이 작동한다.

그러면 여기서 사용된 Multi-headed Attention은 무엇일까?

Self-Attention 메커니즘을 여러 개의 서로 다른 선형 변환을 통해 병렬로 수행하면, 각각의 어텐션 헤드는 다른 관점에서 입력 시퀀스를 조사하고, 서로 다른 문맥 정보를 학습할 수 있지 않을까?
Multi-headed Attention은 바로 위의 형태를 바탕으로 다수의 어텐션 헤드의 결과를 다시 결합되어 최종적인 어텐션 표현을 생성하는 방법이다.
수식으로 살펴보자.
우리는 Attention의 식이 다음인 것을 알고있다.

이전 설명에 따라 여러 개의 서로 다른 선형 변환을 통해 병렬로 수행하면 다음과 같다.

즉, head들은 다음의 식으로 표현된다.

Multi-headed Attention이 작동하는 예시를 보면 다음과 같다.
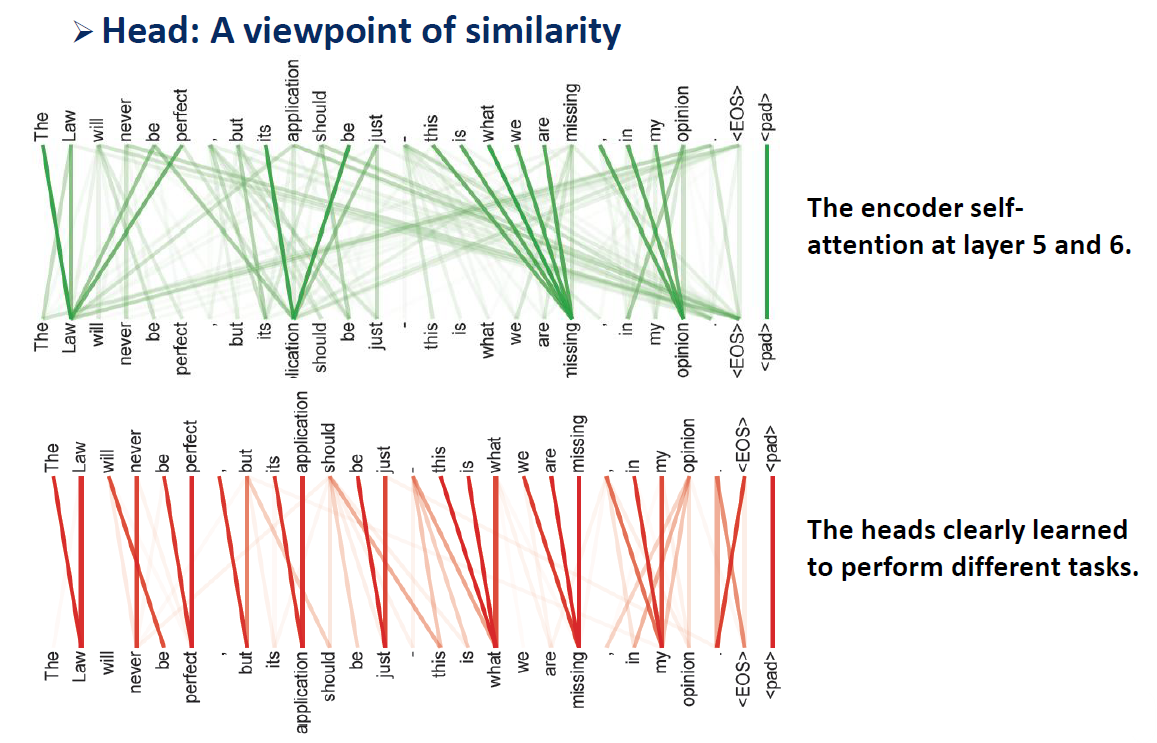
다음은 각각의 어텐션 헤드는 다른 관점에서 입력 시퀀스를 조사하고, 다수의 어텐션 헤드의 결과를 다시 결합되어 최종적인 어텐션 표현을 생성하는 방법은 다음과 같다.


인코더에서 이제 Feed Forward 부분이 남았다. 이 부분은 실제로는 Point wise Feed Forward라고 불리며 다음의 형태를 가지고 있다.

Pointwise Feed Forward는 각 위치(position)별로 독립적으로 작동하는 두 개의 완전히 연결된(feed-forward) 레이어로 구성된다. 이 레이어는 입력 벡터를 받아서 비선형 변환을 수행하고, 출력 벡터를 생성한다.
일반적으로 Pointwise Feed Forward는 두 개의 선형 변환 레이어와 활성화 함수로 구성된다. 입력 벡터에 첫 번째 선형 변환을 적용한 후, 활성화 함수(예: ReLU)를 적용하여 비선형성을 도입한다. 그런 다음, 두 번째 선형 변환을 적용하여 최종 출력을 얻는다.
Pointwise Feed Forward는 각 위치의 입력을 독립적으로 처리하기 때문에, 문장의 다른 위치에서 발생하는 정보를 캡처하고 조합할 수 있다. 이를 통해 모델은 문장 내의 다양한 문맥 정보를 이용하여 특징을 추출하고, 이를 기반으로 다음 단어를 예측하거나 인코딩된 입력을 변환할 수 있다.
Pointwise Feed Forward는 모델의 표현 능력을 향상시키고, 비선형성을 도입하여 모델이 더 복잡한 함수를 학습할 수 있도록 도와준다. 또한, 병렬 처리가 가능하므로 모델의 속도와 효율성을 향상시키는 데 도움이 된다.
생각해보니, 1개를 빼먹었다. 바로 Positional Encoding이다.
Positional Encoding은 Transformer 모델이 순서 정보를 알려주지 않는 입력 시퀀스를 다루기 때문에, 위치 인코딩은 모델이 문장 내의 단어 순서를 고려할 수 있도록 도와준다.
위치 인코딩은 임베딩 공간에 시퀀스 내의 각 단어의 상대적인 위치를 나타내는 벡터를 추가하는 방식으로 수행된다. 이렇게 인코딩된 벡터는 단어 임베딩과 합산되어 최종 입력 표현을 형성한다.
일반적으로, 위치 인코딩은 사인(Sine) 함수와 코사인(Cosine) 함수의 조합을 사용하여 계산된다. 위치 인코딩 벡터의 각 차원은 시퀀스 내의 해당 위치와 함께 특정 주파수를 나타내는 함수 값을 가지게 된다. 이러한 주기성을 통해 모델은 단어의 상대적인 위치 정보를 파악할 수 있다.
즉, Positional Encoding은 모델이 단어의 순서를 학습하는 데 도움을 주며, 임베딩 공간에 단어의 위치를 명시적으로 나타내는 방식이다.

이렇게 들어온것을 Positional Encoding을 통해 적용하면 다음과 같다.

Positional Encoding 값을 나타낸 것이다.

Add & Norm은 각각의 Multi head attention과 feed forward의 Residual 형태이다. 즉, 다음의 식으로 표현된다.

즉, 위의 인코더를 총합하면 다음과 같이 나온다.

다시 Transformer의 전체 모델로 돌아가서 이전 형태의 layer로 표현해보자.

2개의 적층된 인코더와 디코더로 구성된다면 다음과 같이 변할 것이다.

각각의 인코더의 출력은 어텐션 벡터 𝐾 및 𝑉 세트로 두자. encoder-decoder attention layer에서 이들을 활용할 것이다. 그렇게 적용되면 다음의 그림과 같을 것이다.
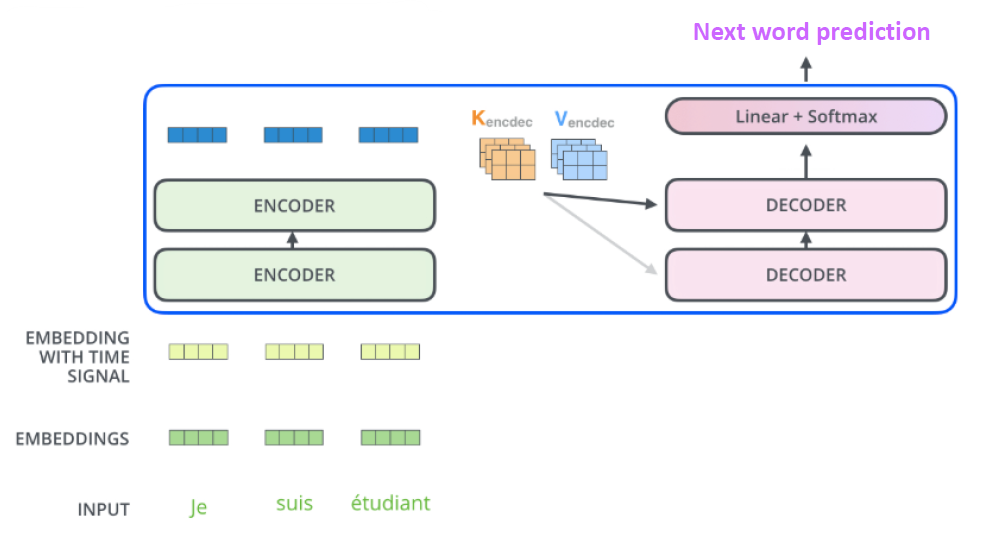
디코더의 자체 주의 레이어는 출력 시퀀스의 이전 위치에만 위칠할 수 있다.
즉, 인코더-디코더 어텐션은 디코더의 현재 위치에서 인코더의 모든 위치에 대한 어텐션 가중치를 계산한다.
추가로 디코더에 있는 masked decoder는 이전에 생성된 출력에 대한 셀프 어텐션만 사용된다. 즉, 이후에 생성된 건 사용못한다는 말이다.

masked multi-head attention이므로 Encoder decoder attention이 사용된다. Encoder decoder attention은 쿼리는 이전 디코더 층에서 가져오고, 키와 값은 인코더의 출력에서 가져옵니다.
마지막으로 출력되는 부분을 간소화해서 보면 다음과 같다.
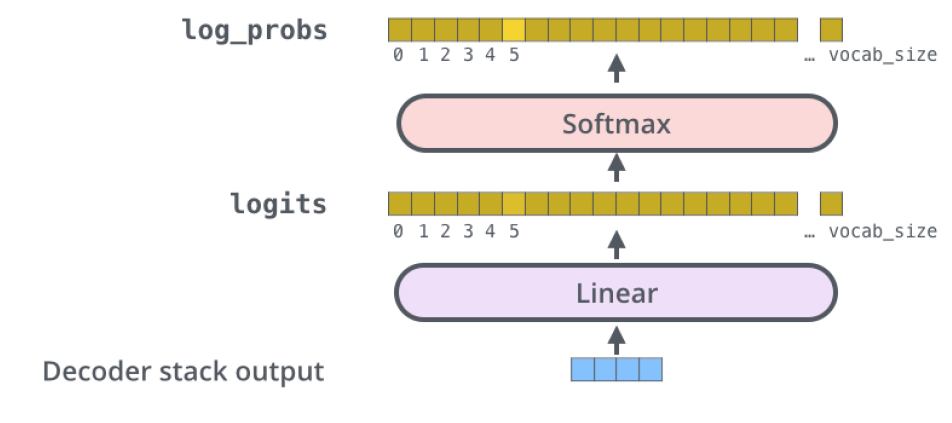
Linear 레이어는 디코더 스택에 의해 생성된 벡터를 logits 벡터라고 불리는 훨씬 더 큰 벡터로 투영하는 간단한 완전히 연결된 신경망이다.
그 다음 소프트맥스 레이어는 그 점수들을 확률로 변환한다(모두 양수이며, 총합은 1.0이 됩니다).
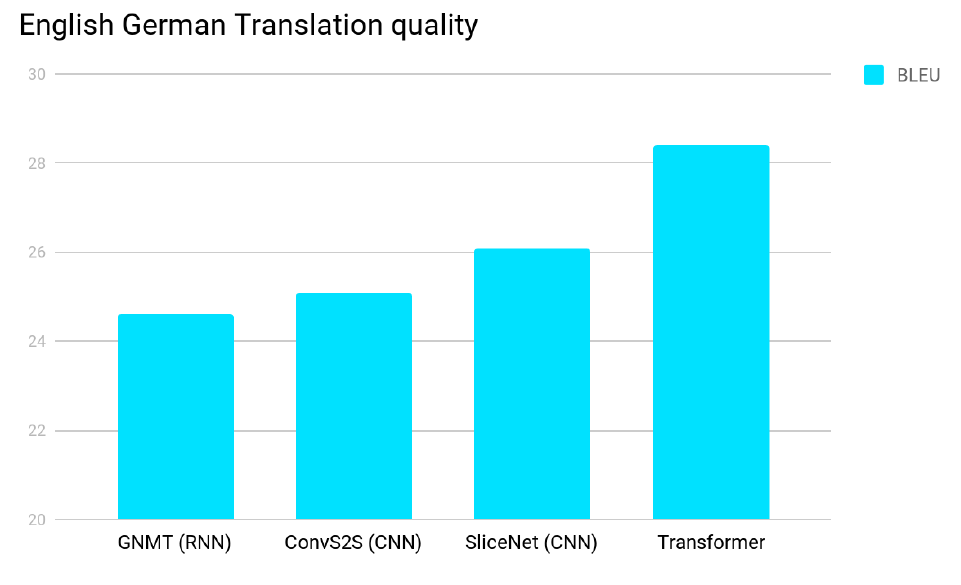
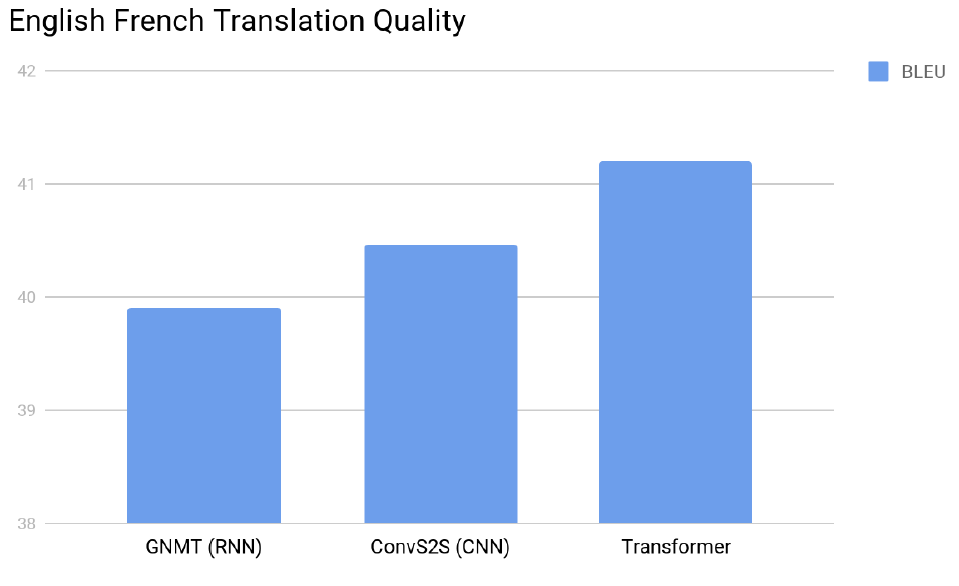
마지막으로 Transformer의 성능에 대해서 보고 마친다.

'인공지능' 카테고리의 다른 글
| Chapter 8 Small Nets and EfficientNet (1) | 2023.05.20 |
|---|---|
| Chapter 7 Generative Adverislal Network (0) | 2023.05.20 |
| Chapter 5 RNN, LSTM, GRU (1) | 2023.05.19 |
| Chapter 4 CNN Structures (1) | 2023.05.19 |
| Diffusion Model (0) | 2023.04.01 |



