Markov Decision Processes (MDP)는 강화 학습을 위한 환경을 공식적으로 설명하며, 환경을 완전히 관찰할 수 있는 경우 거의 모든 RL 문제는 MDP로 공식화할 수 있다. 그렇다고 부분적으로 관찰 가능한 문제를 MDP로 변환할 수 없는 것은 아니다.
여기서부터는 action, state, reward를 행동, 환경, 보상으로 섞어쓸 것이다.
Markov Property
• 미래는 현재 주어진 과거와 독립적이다
• state는 기록에서 모든 관련 정보를 캡처한다
• state가 알려지면 기록을 버릴 수 있다
즉 . state는 미래에 대한 충분한 통계이다

State Transition Matrix(상태 전이 행렬)
• Markov 상태 𝑠 및 후속 상태 𝑠′의 경우 상태 전이 확률은 다음과 같이 정의된다.

• state 전환 매트릭스 𝑃는 모든 전환 확률을 정의한다
• state s는 행렬의 각 행의 합이 1인 모든 후속 state s'이다

Markov Process
마르코프 과정은 메모리가 없는 무작위 과정이다. 예를 들어, 마르코프 특성을 갖는 무작위 상태인 𝑆1, 𝑆2, . . . 의 순서대로 발생하는 시퀀스로 나타낼 수 있다.

Example: Student Markov Chain
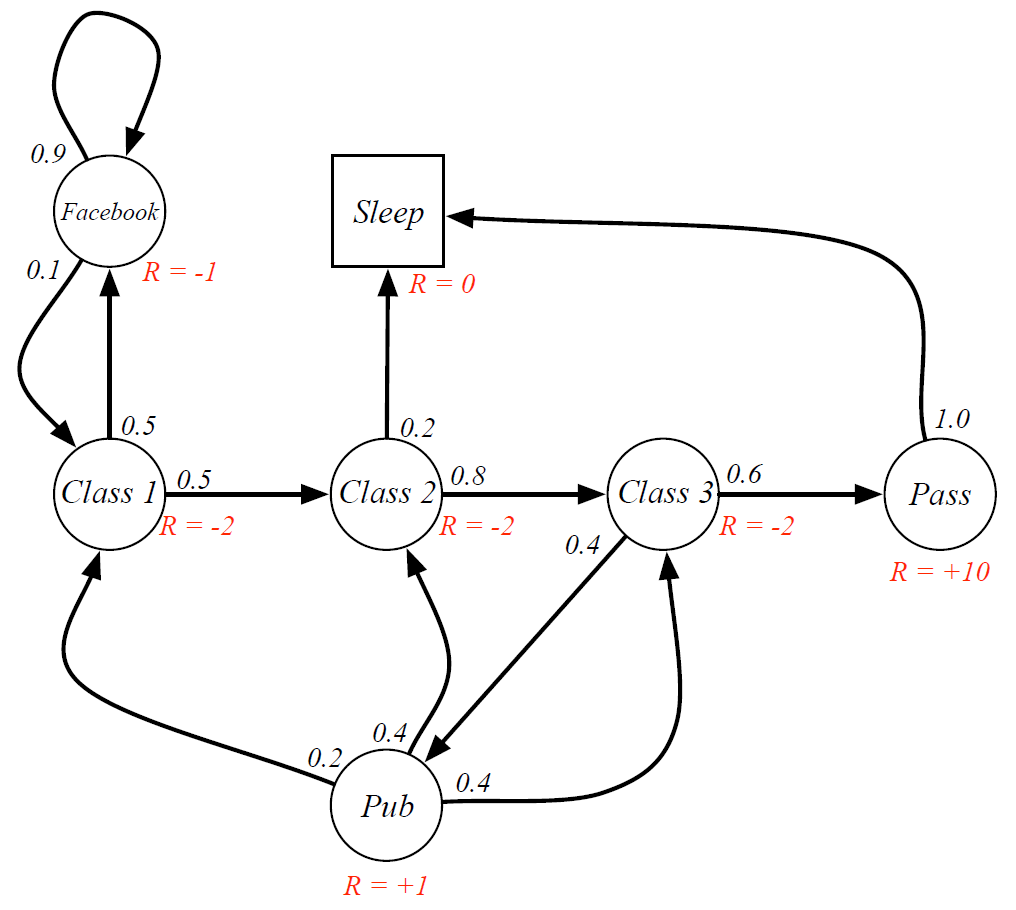
아래의 마르코프 체인이 있다고 가정하자

전체가 관찰 가능하기 때문에, 우리가 정의했던 P를 통해 다음의 행렬을 얻을 수 있다.

Markov Reward Process
Markov 보상 프로세스는 값(Reward)이 있는 Markov 체인이다. 다음으로 정의된다.

이 정의로 보면 state에 따른 discount factor를 통해 R을 구하는 방식이다. 일단 첫 step만 나타낸다면, 다음과 같이 나타낼수 있을것이다.
(Discounted) Return
discount factor를 통해 R을 구하는 방식을 알아야되기 때문에 이를 확인하면 아래와 같다.

• 할인율 𝛾∈[0,1]은 미래 보상의 현재 가치다
• 𝑘+1단계 후 보상 𝑅을 받는 값은 𝛾𝑘𝑅이다
• 이것은 지연된 보상보다 즉각적인 보상을 중요시한다
• 𝛾이 0에 가까울수록 "근시" 평가
• 𝛾이 1에 가까울수록 '원시적' 평가로 이어짐
왜 discount factor를 적용하는 것일까?
대부분의 Markov 보상 및 결정 프로세스는 할인된다 이는 순환 Markov 프로세스에서 무한 반환 방지를 위해서 그렇다. 추가적으로 미래에 대한 불확실성이 완전히 표현되지 않을 수 있고, 보상이 금전적인 경우 즉각적인 보상은 지연된 보상보다 더 많은 이자를 받을 수 있다. 일반적으로 동물/인간의 행동은 즉각적인 보상을 선호하기 때문에, 때때로 할인되지 않은 Markov 보상 프로세스를 사용할 수 있다.(예: 𝛾= 1 )
Value Function
가치 함수 𝑣(𝑠)는 상태 𝑠의 장기적인 가치를 제공한다. 이는 아래 수식으로 확인할 수 있다.

이전의 마르코프 체인에 discount factor와 value function을 적용하면 다음과 같다. 여기서 discount factor는 0.5이다.

discount factor에 따라 다시 구해보면 아래와 같은 그림이 된다.

Bellman Equation for MRPs
• 가치 함수는 두 부분으로 분해될 수 있다
• 즉각적인 보상 𝑅𝑡+1
• 후속 상태의 할인된 값 𝛾𝑣(𝑆𝑡+1)
이를 식으로 표한하면 다음과 같다.

그림으로 표현하면 다음과 같이 표현될 것이다. 두 부분으로 분해되기 때문에
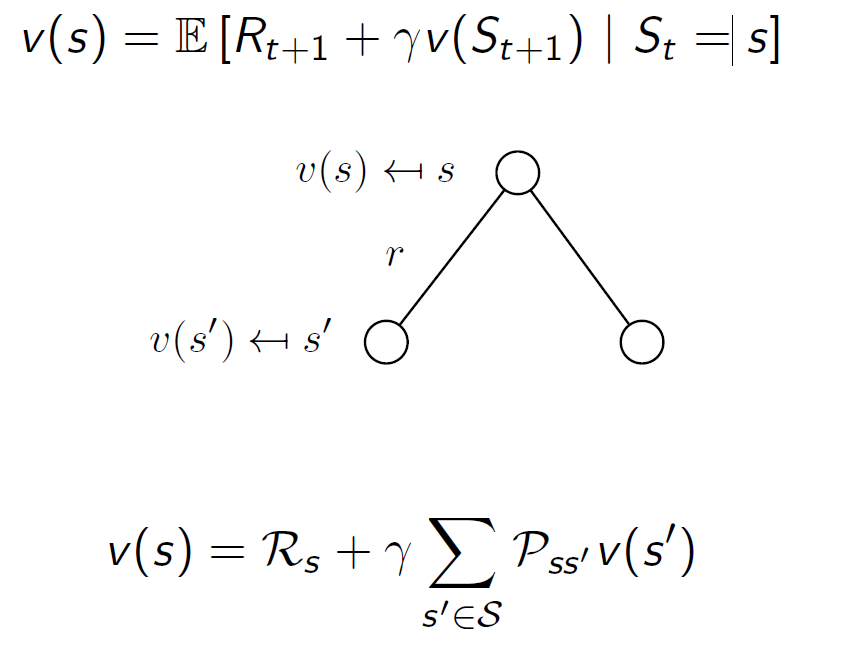
Markov Decision Process
• Markov 결정 프로세스(MDP)는 결정이 포함된 Markov 보상 프로세스이다다. 따라서 모든 상태가 Markov인 환경이다.

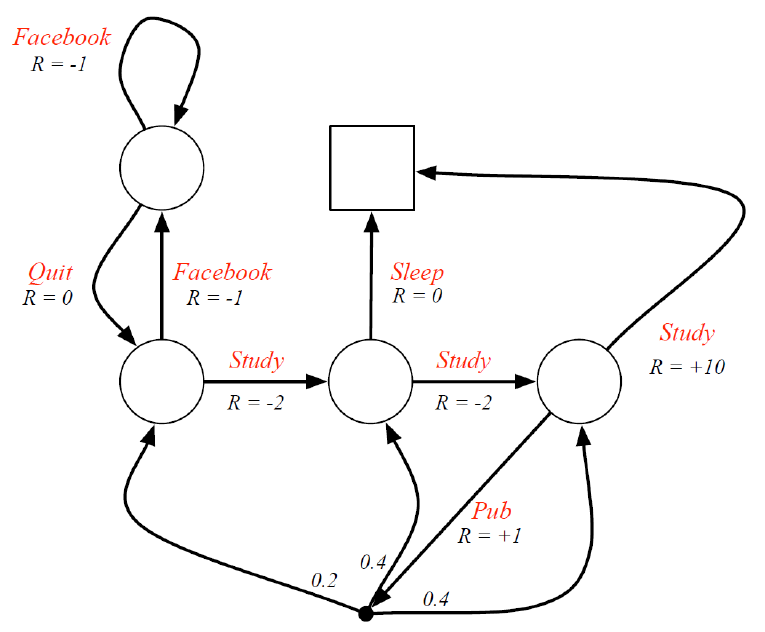
아까 예시를 들었던 student는 MDP로 볼 수 있다.
Policies
• 정책은 에이전트의 행동을 완전히 정의한다
• MDP 정책은 현재 상태에 따라 달라진다(이전에 했던 행동이 아님)
• 즉, 정책은 고정적(시간 독립적), 𝐴𝑡~𝜋(∙|𝑆𝑡),∀𝑡>0

• 주어진 MDP =𝑆,𝐴,𝑃,𝑅,𝛾 및 정책 𝜋
• 상태 시퀀스 𝑆1,𝑆2. . .는 마르코프 프로세스 <𝑆,𝑃𝜋>
• 상태 및 보상 시퀀스 𝑆1,𝑅2,𝑆2, . . . Markov 보상 프로세스< 𝑆,𝑃𝜋,𝑅𝜋,𝛾>
따라서 식으로 표현하면 다음과 같다.

Value Function
value function은 state-value function과 action-value function이 있다.
- 상태-가치 함수(State-Value Function): 상태-가치 함수는 주어진 상태에서 에이전트가 평균적으로 얻을 수 있는 기대 보상을 나타냅니다. 즉, 특정 상태에서 정책(policy)에 따라 행동을 선택하고 실행했을 때 얻을 수 있는 보상의 기댓값입니다. 상태-가치 함수는 다음과 같이 표현됩니다: V(s) = E[R | s], 여기서 V(s)는 상태 s에서의 가치를 나타내며, E는 기댓값을 의미하고, R은 에피소드(episode)에서 얻는 보상을 나타냅니다. 상태-가치 함수는 강화학습에서 가장 기본적이고 중요한 개념 중 하나입니다.
- 행동-가치 함수(Action-Value Function): 행동-가치 함수는 특정 상태에서 특정 행동을 선택했을 때 얻을 수 있는 기대 보상을 나타냅니다. 즉, 상태와 행동의 조합에 따라 얻을 수 있는 보상의 기댓값입니다. 행동-가치 함수는 다음과 같이 표현됩니다: Q(s, a) = E[R | s, a], 여기서 Q(s, a)는 상태-행동 쌍 (s, a)에서의 가치를 나타내며, E는 기댓값을 의미하고, R은 에피소드에서 얻는 보상을 나타냅니다. 행동-가치 함수는 상태와 행동의 조합에 따른 가치를 평가하는 데 사용되며, 최적의 정책을 찾는 강화학습 알고리즘에서 중요한 역할을 합니다.

Bellman Expectation Equation
• 상태 가치 함수는 다시 즉각적인 보상과 후속 상태의 할인된 가치로 분해될 수 있다.

• 액션 가치 함수도 유사하게 분해할 수 있다.



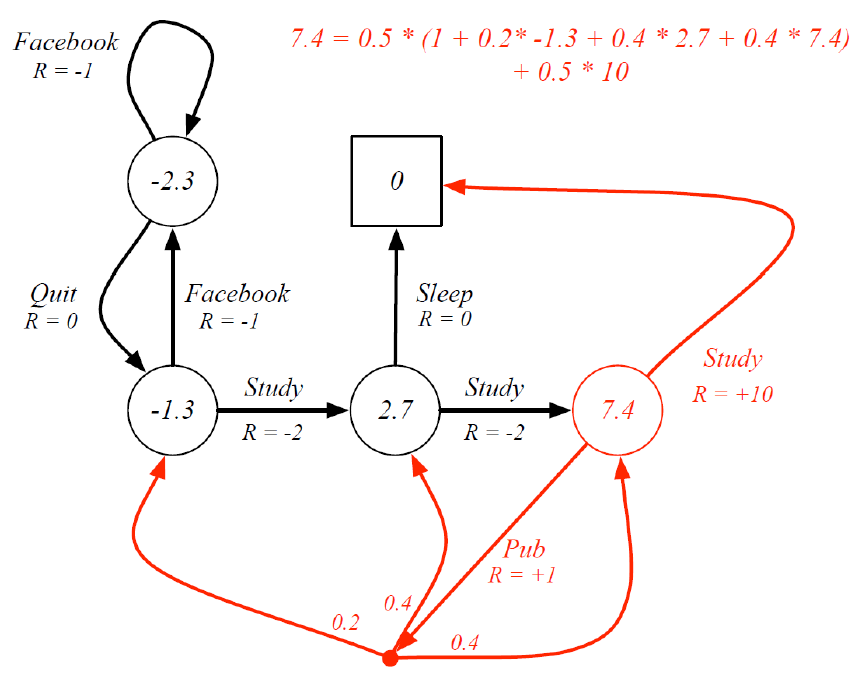
이전의 Student MDP에 state-value fucntion을 적용하면 다음과 같다.

Bellman Expectation Equation in Matrix Form
벨만 기대 방정식(Bellman Expectation Equation)은 현재 상태에서 다음 상태로 전이될 때의 가치와 보상을 고려하여 현재 상태의 가치를 예측한다.
벨만 기대 방정식을 행렬 형태로 표현하면 다음과 같다:
V = R + γPV
• V는 현재 상태의 상태-가치 함수를 나타내는 열 벡터
• R은 현재 상태에서 즉시 받는 보상을 나타내는 열 벡터
• γ는 할인율(discount factor)로, 0과 1 사이의 값입니다. 미래의 보상을 현재보다 덜 가치있게 여기는 역할
• P는 상태 전이 확률 행렬로, 상태 전이 확률을 나타내는 행렬
따라서 벨만 기대 방정식은 현재 상태의 가치 V를 현재 상태에서 받는 즉시 보상 R과 다음 상태의 가치 P*V를 고려하여 예측한다. 할인율 γ는 미래 보상의 중요성을 조절하는 역할을 하며, 높은 값일수록 미래 보상에 더 중점을 둔라고 이전에 설명했다.
따라서 식을 다음과 같이 전개하면 다음의 matricx form을 볼 수 있다.

• 계산 복잡도는 n 상태에 대해 O(n^3 )
• 소규모 MDP에만 가능한 다이렉트 솔루션
• 대규모 MRP에 대한 많은 반복 방법이 있다
이제 기본적인 policy, reward등에 대해서 계산하는 방법들을 배웠다.
어떻게 reward를 maximize하고 최적의 policy를 찾고, 더 좋은 policy를 결정하는 법에 대해서 들어가보자.
Optimal Value Function
최적 가치 함수(Optimal Value Function)는 주어진 환경에서 에이전트가 얻을 수 있는 최대 기대 보상을 나타낸다.
최적 가치 함수를 표현하기 위해 두 가지 종류의 가치 함수를 정의할 수 있다:
- 최적 상태-가치 함수(Optimal State-Value Function): 최적 상태-가치 함수는 각 상태에 대해 에이전트가 최적의 정책을 따랐을 때 얻을 수 있는 최대 기대 보상을 나타냅니다. 최적 상태-가치 함수는 다음과 같이 표현됩니다: V*(s) = max[Q*(s, a)], 여기서 V*(s)는 상태 s에서의 최적 가치를 나타내며, Q*(s, a)는 최적 행동-가치 함수를 의미합니다. max 연산은 가능한 모든 행동에 대한 가치를 비교하여 최대 값을 선택하는 것을 의미합니다.
- 최적 행동-가치 함수(Optimal Action-Value Function): 최적 행동-가치 함수는 각 상태와 행동 조합에 대해 에이전트가 최적의 정책을 따랐을 때 얻을 수 있는 최대 기대 보상을 나타냅니다. 최적 행동-가치 함수는 다음과 같이 표현됩니다: Q*(s, a) = max[R + γV*(s')], 여기서 Q*(s, a)는 상태-행동 쌍 (s, a)에서의 최적 가치를 나타내며, R은 즉시 받는 보상을 의미하고, γ는 할인율(discount factor)입니다. V*(s')는 다음 상태 s'에서의 최적 상태-가치 함수를 의미합니다.
최적 가치 함수를 찾기 위해서는 가치 함수를 초기화하고 벨만 최적 방정식(Bellman Optimality Equation)을 반복적으로 적용하여 가치 함수를 업데이트한다. 이를 통해 최적 가치 함수를 점진적으로 추정하고, 최적의 정책을 찾을 수 있다.

Optimal Policy
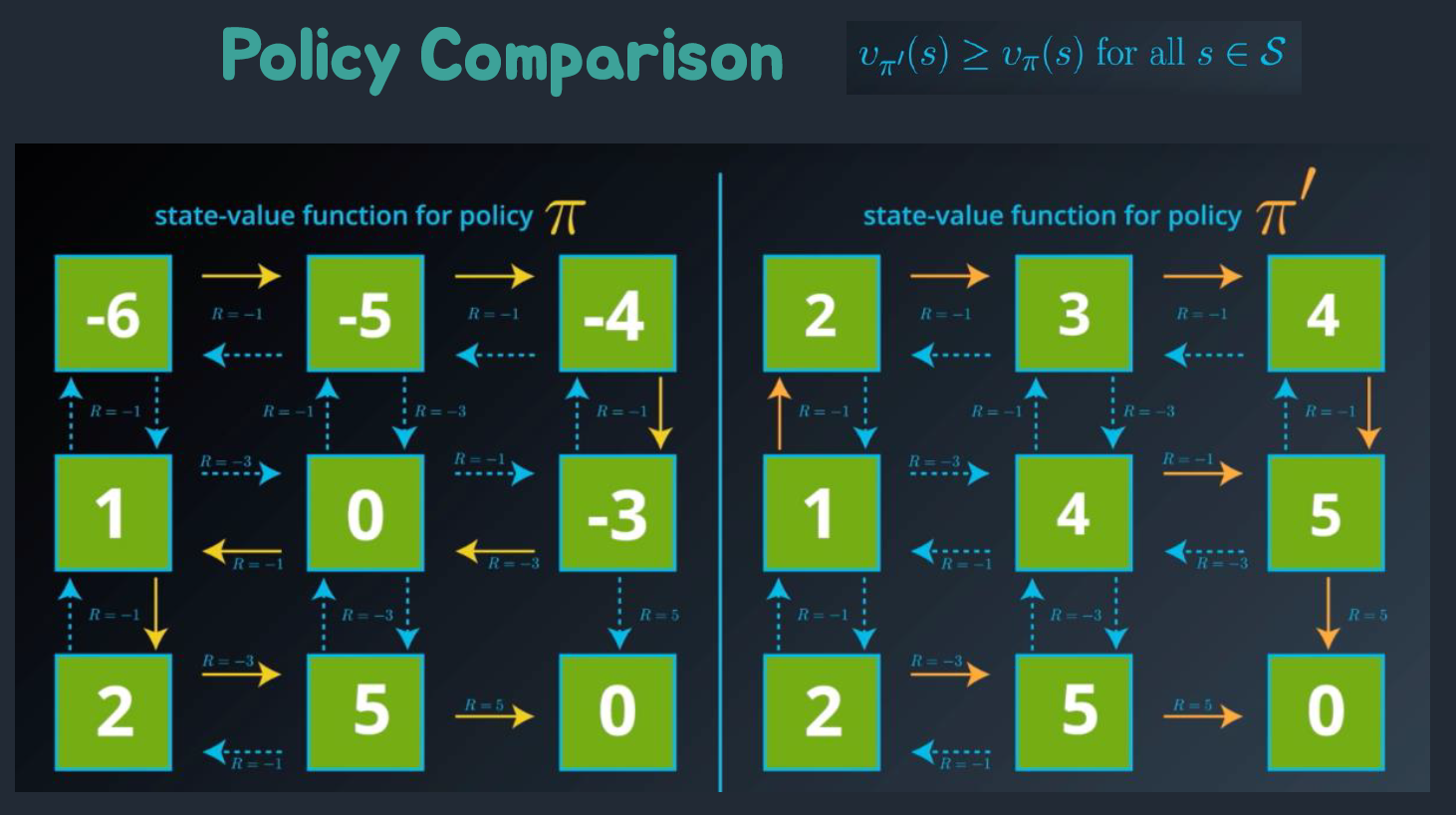
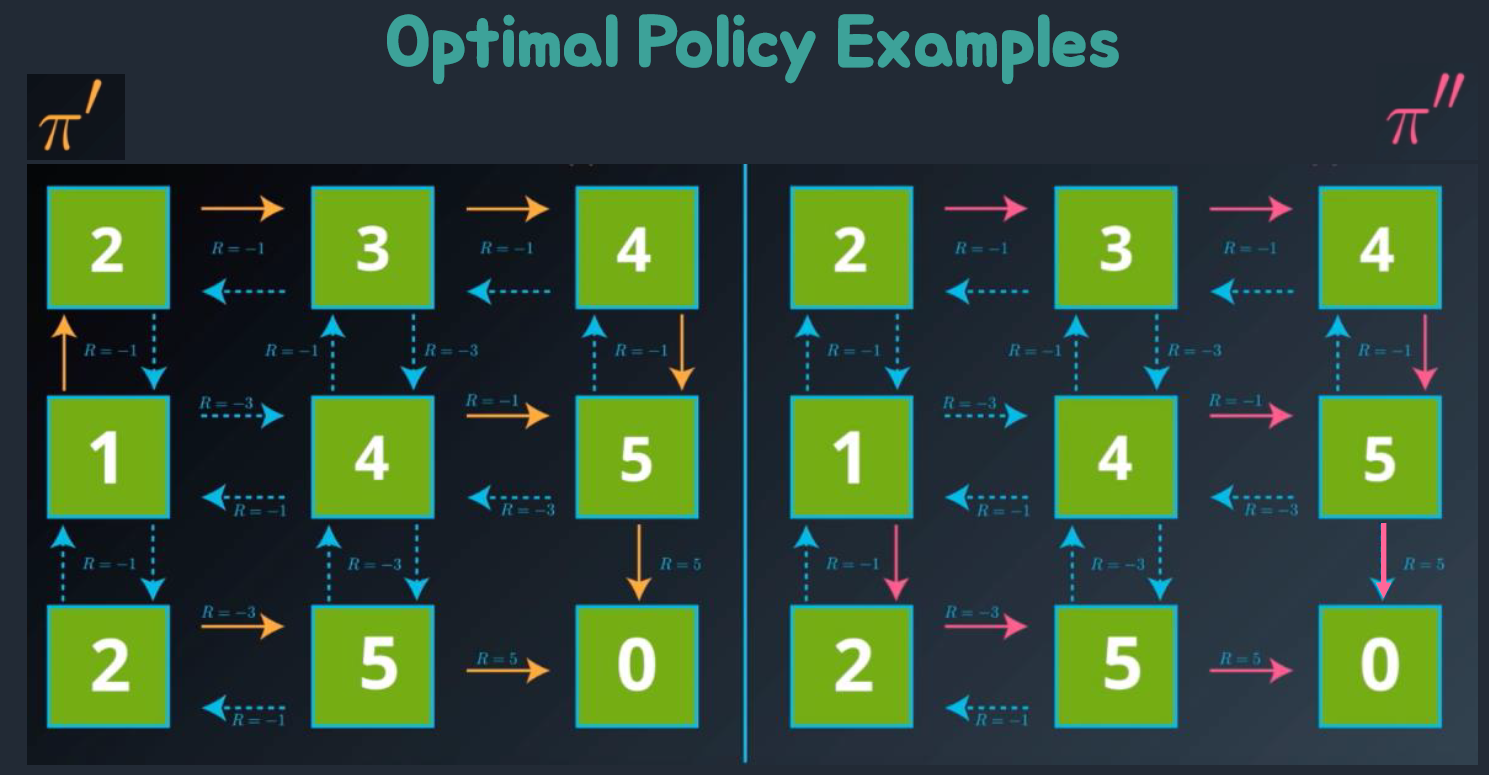
최적 정책(Optimal Policy)은 최적 가치 함수(Optimal Value Function)를 기반으로 결정된다.
강화학습에서 정책은 상태(state)에 따라 에이전트가 선택해야 할 행동(action)을 결정하는 매핑 함수로 나타낸다. 최적 정책은 에이전트가 상태에 따라 선택해야 할 최적의 행동을 결정하는 정책이다.
최적 정책은 최적 가치 함수와 관련되어 있습니다. 최적 상태-가치 함수(V*(s))를 사용하는 최적 정책은 각 상태에서 최적의 행동을 선택하는 방식으로 정의된다. 즉, 최적 정책에서는 각 상태에 대해 최대의 상태-가치를 갖는 행동이 선택됩니다. 따라서 최적 상태-가치 함수를 통해 최적 정책을 알 수 있다.
또한, 최적 행동-가치 함수(Q*(s, a))를 사용하는 최적 정책은 상태와 행동의 조합에 따라 최적의 행동을 선택하는 방식으로 정의된다. 최적 행동-가치 함수에서는 각 상태와 행동 조합에 대해 최대의 행동-가치를 갖는 행동이 선택된다. 따라서 최적 행동-가치 함수를 통해 최적 정책을 알 수 있다.
최적 정책을 찾기 위해서는 최적 가치 함수를 추정하고, 추정된 최적 가치 함수를 기반으로 최적 정책을 결정한다. 주로 가치 반복(Value Iteration)이나 정책 반복(Policy Iteration)과 같은 알고리즘을 사용하여 최적 가치 함수와 최적 정책을 동시에 추정하고 개선한다.
따라서 최적 정책은 강화학습에서 에이전트가 환경과 상호작용하며 최대의 보상을 얻을 수 있는 행동 선택을 도와준다.

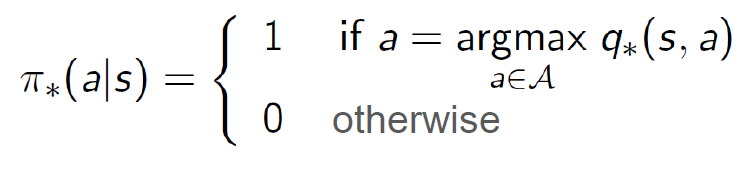
Bellman Optimality Equations
벨만 최적 방정식(Bellman Optimality Equations)은 강화학습에서 최적 가치 함수와 최적 정책을 찾기 위해 사용되는 중요한 방정식이다. 벨만 최적 방정식은 현재 상태에서 가능한 모든 행동에 대해 최적 가치를 계산하기 위한 재귀적인 관계를 제공한다.
벨만 최적 방정식을 상태-가치 함수와 행동-가치 함수로 나누어 설명할 수 있다.
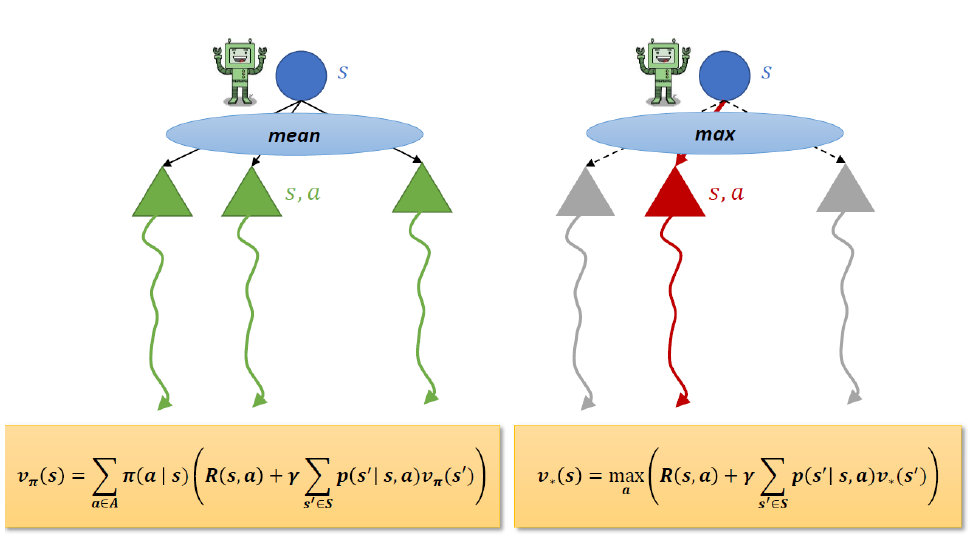
- 상태-가치 함수의 벨만 최적 방정식: 최적 상태-가치 함수의 벨만 최적 방정식은 다음과 같이 표현됩니다: V*(s) = max[Q*(s, a)], 여기서 V*(s)는 상태 s에서의 최적 상태-가치를 나타내며, Q*(s, a)는 최적 행동-가치 함수를 의미합니다. 최적 상태-가치 함수는 현재 상태에서 가능한 모든 행동에 대한 최적 행동-가치를 고려하여 가장 높은 가치를 선택합니다.
- 행동-가치 함수의 벨만 최적 방정식: 최적 행동-가치 함수의 벨만 최적 방정식은 다음과 같이 표현됩니다: Q*(s, a) = max[R + γV*(s')], 여기서 Q*(s, a)는 상태-행동 쌍 (s, a)에서의 최적 가치를 나타내며, R은 즉시 받는 보상을 의미하고, γ는 할인율(discount factor)입니다. V*(s')는 다음 상태 s'에서의 최적 상태-가치 함수를 의미합니다. 최적 행동-가치 함수는 현재 상태와 행동 조합에 대해 가능한 모든 다음 상태에서의 최적 상태-가치를 고려하여 가장 높은 가치를 선택합니다.
벨만 최적 방정식은 최적 가치 함수를 업데이트하기 위해 사용된다. 주어진 환경에서 최대의 보상을 얻기 위해 최적 가치 함수를 반복적으로 추정하고 개선하는 데 사용된다. 이를 통해 최적 가치 함수를 구하고, 이에 기반하여 최적 정책을 결정할 수 있다. 벨만 최적 방정식은 값 반복(Value Iteration)과 정책 반복(Policy Iteration)과 같은 알고리즘에서 주요한 개념으로 활용된다. 따라서 다음 그림이 유효하다.


Solving the Bellman Optimality Equation
벨만 최적 방정식(Bellman Optimality Equation)을 해결하는 것은 강화학습에서 최적 가치 함수를 추정하고, 이를 통해 최적 정책을 결정하는 과정이다. 벨만 최적 방정식을 해결하기 위해서는 반복적인 방법을 사용한다.
벨만 최적 방정식을 해결하는 일반적인 접근 방법은 다음과 같다:
- 초기화: 최적 가치 함수를 초기값으로 설정합니다. 초기값으로는 임의의 값을 사용하거나 모든 상태에 대해 초기값을 동일하게 설정할 수 있습니다.
- 가치 함수 업데이트: 벨만 최적 방정식을 기반으로 현재의 가치 함수를 업데이트합니다. 최적 상태-가치 함수인 경우에는 다음과 같이 업데이트됩니다: V_{k+1}(s) = max_a [Q_k(s, a)], 여기서 V_{k+1}(s)는 k+1번째 반복에서의 상태 s의 가치를 나타내며, Q_k(s, a)는 k번째 반복에서의 행동-가치 함수를 의미합니다. 모든 상태에 대해 최적 행동-가치를 계산하여 각 상태의 최적 상태-가치를 업데이트합니다.
- 행동-가치 함수 업데이트: 최적 행동-가치 함수를 업데이트합니다. 최적 행동-가치 함수인 경우에는 다음과 같이 업데이트됩니다: Q_{k+1}(s, a) = R(s, a) + γV_k(s'), 여기서 Q_{k+1}(s, a)는 k+1번째 반복에서의 상태-행동 쌍 (s, a)의 가치를 나타내며, R(s, a)는 즉시 받는 보상을 의미하고, γ는 할인율(discount factor)입니다. V_k(s')는 k번째 반복에서의 다음 상태 s'의 가치를 의미합니다.
- 수렴 검사: 가치 함수가 충분히 수렴할 때까지 2번과 3번의 단계를 반복합니다. 가치 함수가 수렴하는 조건은 알고리즘의 종료 조건으로 설정되는데, 일반적으로는 두 가치 함수 간의 차이가 작아지거나 일정한 값 미만이 될 때 수렴으로 간주합니다.
- 정책 결정: 최적 가치 함수를 기반으로 최적 정책을 결정합니다. 최적 상태-가치 함수인 경우에는 각 상태에서 최대 가치를 가지는 행동을 선택하여 최적 정책을 구성합니다. 최적 행동-가치 함수인 경우에는 각 상태와 행동 조합에서 최대 가치를 가지는 행동을 선택하여 최적 정책을 구성합니다.
벨만 최적 방정식을 해결하는 것은 최적 가치 함수와 최적 정책을 찾는 과정이다. 이를 통해 강화학습 에이전트는 주어진 환경에서 최대의 보상을 얻을 수 있는 최적의 행동 선택을 학습하게 된다.
반복으로 푸는 방식은 다음과 같다.
• Policy Iteration
• Value Iteration
• SARSA
• Q-Learning
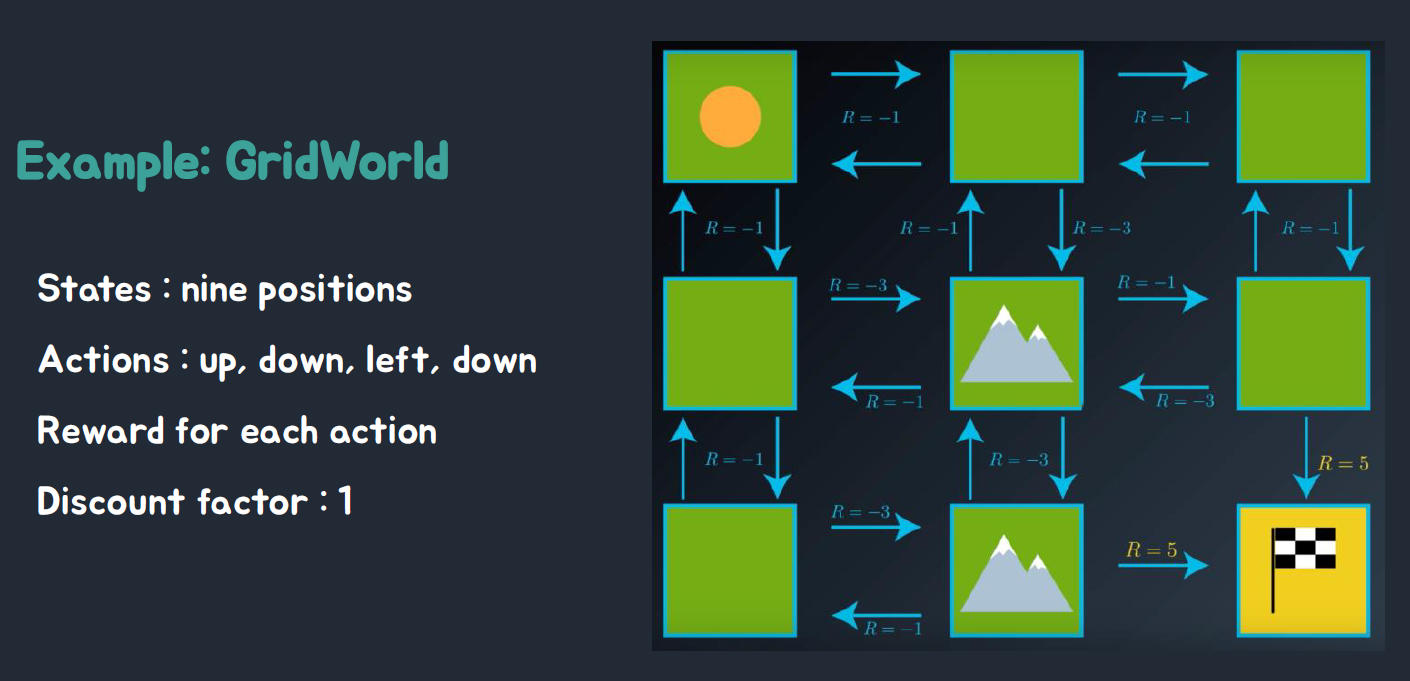
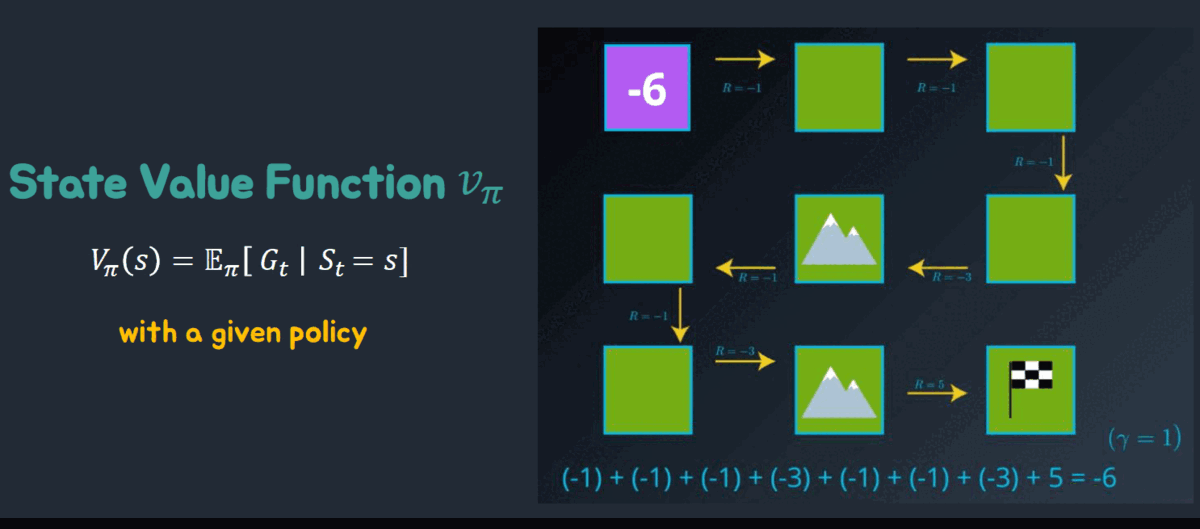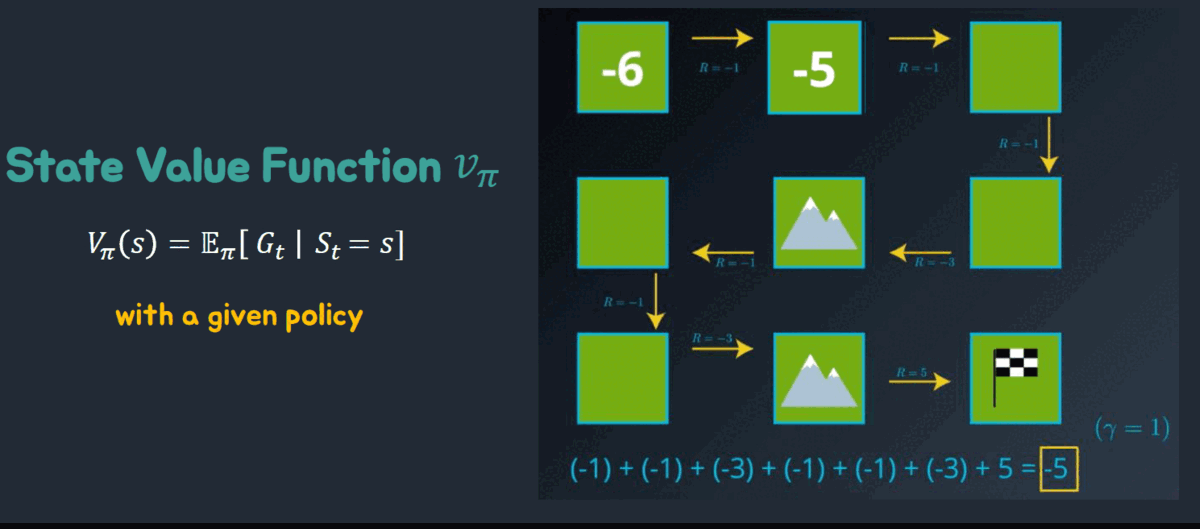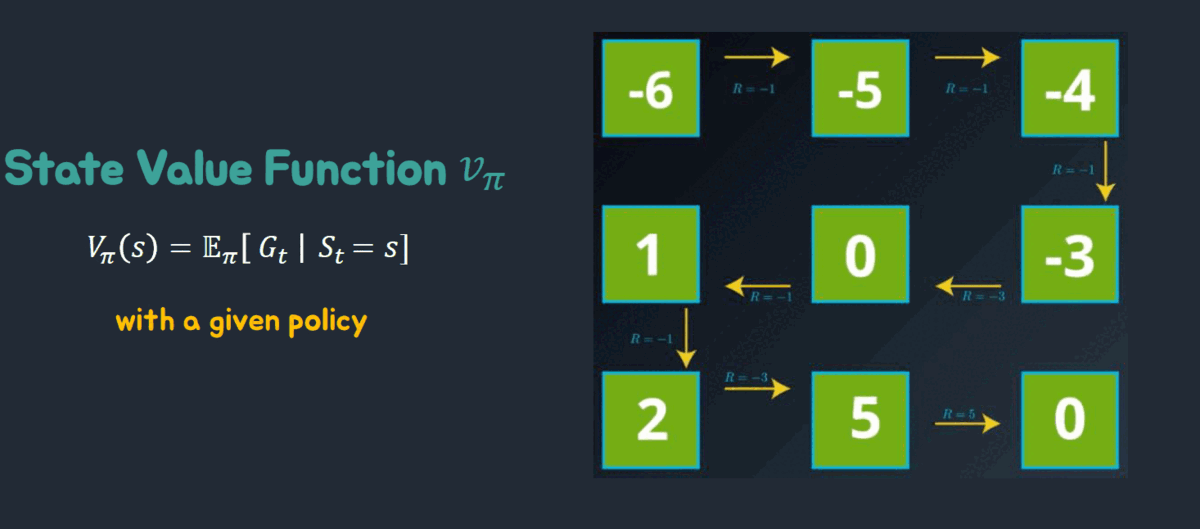
지금까지 했던걸 예제로 적용하면 다음과 같다.
예제 환경은 다음과 같다.


'강화학습' 카테고리의 다른 글
| Chapter6. Model-Free Control (0) | 2023.05.22 |
|---|---|
| Chapter 5. Model-free Prediction (1) | 2023.05.21 |
| Chapter4. Model-based Planning (0) | 2023.05.21 |
| Chapter 2 Reinforcement Learning Overview (0) | 2023.05.21 |
| Chapter 1 Introduction (0) | 2023.05.20 |



