지금까지 공식을 배웠다면 이를 적용하는 것에 대해서 알아보자.
Planning(계획)과 Reinforcement Learning(강화학습)은 강화학습의 두 가지 중요한 접근 방법이 있다. 각각의 방법은 다음과 같이 설명된다:
- Planning(계획): 계획은 미리 환경 모델을 알고 있고, 그 모델을 기반으로 일련의 행동을 예측하고 최적의 행동 계획을 세우는 프로세스입니다. 계획에서는 환경의 동작을 모델링하고 이 모델을 사용하여 가능한 행동 순서를 시뮬레이션하고 평가합니다. 계획은 주어진 환경에서 최적의 행동 시퀀스를 찾는 데 유용합니다.
- 환경 모델 구축: 주어진 환경에 대한 모델을 구축합니다. 모델은 상태 전이 확률과 보상 함수를 포함합니다.
- 계획 수립: 모델을 기반으로 가능한 행동 시퀀스를 탐색하고 평가하여 최적의 행동 계획을 수립합니다.
- 계획 실행: 수립된 계획에 따라 행동을 선택하고 실행합니다.
- Reinforcement Learning(강화학습): 강화학습은 주어진 환경에서의 상호작용을 통해 에이전트가 최적의 행동을 스스로 학습하는 프로세스입니다. 강화학습에서는 환경 모델을 사전에 알지 못하고, 실제 경험을 통해 행동을 선택하고 보상을 받으면서 최적의 정책을 학습합니다.
- 상태(state): 에이전트가 관찰하는 환경의 상태입니다.
- 행동(action): 에이전트가 특정 상태에서 선택할 수 있는 행동입니다.
- 보상(reward): 에이전트가 행동을 실행한 후 받는 보상입니다.
- 정책(policy): 상태에 따라 행동을 선택하는 정책입니다.
- 가치 함수(value function): 상태 또는 상태-행동 쌍의 가치를 나타내는 함수입니다.
Planning과 Reinforcement Learning은 강화학습에서 서로 보완적인 역할을 한다. Planning은 모델을 알고 있을 때 최적의 행동 계획을 수립하는 반면, Reinforcement Learning은 실제 환경과의 상호작용을 통해 최적의 행동을 학습한다.
좀 더 자세하게 설명하기 위해서 다음을 설명하겠다.
동적 프로그래밍이란?
• 재귀적인 방식으로 더 간단한 하위 문제로 분해하여 복잡한 문제를 단순화한다
• 하위 문제를 해결하며, 하위 프로그램을 최종 솔루션에 결합하는 방법이다
그렇다면 동적 프로그래밍이 왜 필요할까?
바로 다이나믹 프로그래밍(Dynamic Programming)의 두 가지 특성을 때문이다.
• 최적 부분 구조(Optimal Substructure): 최적의 해결 방법이 부분 문제들의 최적 해결 방법으로 구성될 수 있다
• 최적성의 원리(Principle of Optimality): 최적의 해결 방법은 여러 부분 문제로 분해될 수 있으며, 이러한 부분 문제들은 중복되어 반복적으로 발생한다. 이에 따라 이전에 계산된 해답을 저장해두고 재사용할 수 있다
즉 ,다이나믹 프로그래밍은 문제를 작은 부분 문제들로 분할하고, 이러한 부분 문제들을 반복적으로 해결하여 최적의 해답을 찾는 방법이다. 이때, 부분 문제들은 겹치는 구조를 가지며, 동일한 부분 문제들이 여러 번 반복해서 나타난다.
Markov 결정 프로세스는 두 속성을 모두 만족한다는 것을 우리는 알고 있다.
Bellman 방정식은 재귀 분해를 제공하며, Value function은 솔루션을 저장하고 재사용하기 때문이다.
Planning by Dynamic Programming으로 Planning을 어떻게 진행할까?
먼저, MDP의 완전한 지식을 가정하자. 그러면 주어진 MDP와 정책(policy)을 활용하여 예측(prediction) 또는 제어(control)를 수행할 수 있다.
예측의 경우, 입력으로는 MDP와 정책이 주어지며, 출력으로는 값 함수(value function)를 얻는다.
제어의 경우, 입력으로는 MDP가 주어지며, 출력으로는 최적 값 함수(optimal value function)와 최적 정책(optimal policy)를 얻는다.
예측의 경우, 주어진 MDP와 정책에 대해 값 함수를 계산한다. 값 함수는 각 상태(state)에서의 기대 반환값을 나타내며, 주어진 정책에 따라 상태 전이와 보상을 고려하여 계산된다.
제어의 경우, 주어진 MDP에 대해 최적의 값 함수와 최적 정책을 찾는다. 최적 값 함수는 각 상태에서의 최대 기대 반환값을 나타내며, 최적 정책은 최대 기대 반환값을 제공하는 행동(action)을 선택하는 방식으로 구성된다.
다이나믹 프로그래밍은 MDP 문제에 대해 최적의 값 함수와 정책을 계산하는데 사용되며, 이를 통해 최적의 행동 선택을 가능하게 할 수 있다.
즉, 다음과 같다.

이를 반복해서 얻기 때문에, Iterative Policy Evaluation를 살펴보자.
반복 정책 평가(Iterative Policy Evaluation)는 강화학습에서 주어진 정책에 대한 상태-가치 함수를 추정하는 알고리즘이다. 반복 정책 평가는 벨만 기대 방정식(Bellman Expectation Equation)을 활용하여 가치 함수를 반복적으로 업데이트하여 최적 가치 함수에 수렴하도록 한다.
반복 정책 평가 알고리즘은 다음과 같은 단계로 수행된다:
- 초기화: 상태-가치 함수 V(s)를 임의의 초기값으로 초기화합니다.
- 반복 업데이트: 아래의 식을 반복적으로 적용하여 상태-가치 함수를 업데이트합니다: V(s) = Σₐπ(a|s) Σₛ' Pₐₛₛ' [Rₐₛₛ' + γV(s')], 여기서 s는 상태, a는 행동, π(a|s)는 상태 s에서 행동 a를 선택하는 정책의 확률, Pₐₛₛ'은 상태 s에서 행동 a를 선택하여 다음 상태 s'로 전이될 확률, Rₐₛₛ'은 상태 s에서 행동 a를 선택하여 다음 상태 s'로 전이될 때 받는 보상, γ는 할인율(discount factor)입니다.
- 업데이트 반복: 상태-가치 함수가 수렴할 때까지 2번 단계를 반복합니다. 수렴 조건은 일정한 값 미만의 변화 또는 두 가치 함수 간의 차이가 작아질 때로 정의됩니다.
반복 정책 평가 알고리즘은 주어진 정책에 대한 상태-가치 함수를 점진적으로 추정하고, 이를 통해 각 상태에서의 기대 반환값을 알 수 있다. 이를 통해 에이전트는 주어진 정책에 따라 최적의 행동을 선택할 수 있게 된다. 반복 정책 평가는 값 반복(Value Iteration)과 같은 알고리즘의 기반 구성 요소로 사용되며, 최적 가치 함수를 추정하는 데 활용된다.
따라서 아래로 간단하게 정의할 수 있다.

벨만 기대 방정식을 infinite하게 적용하면 다음과 같이 표현할 수 있다.
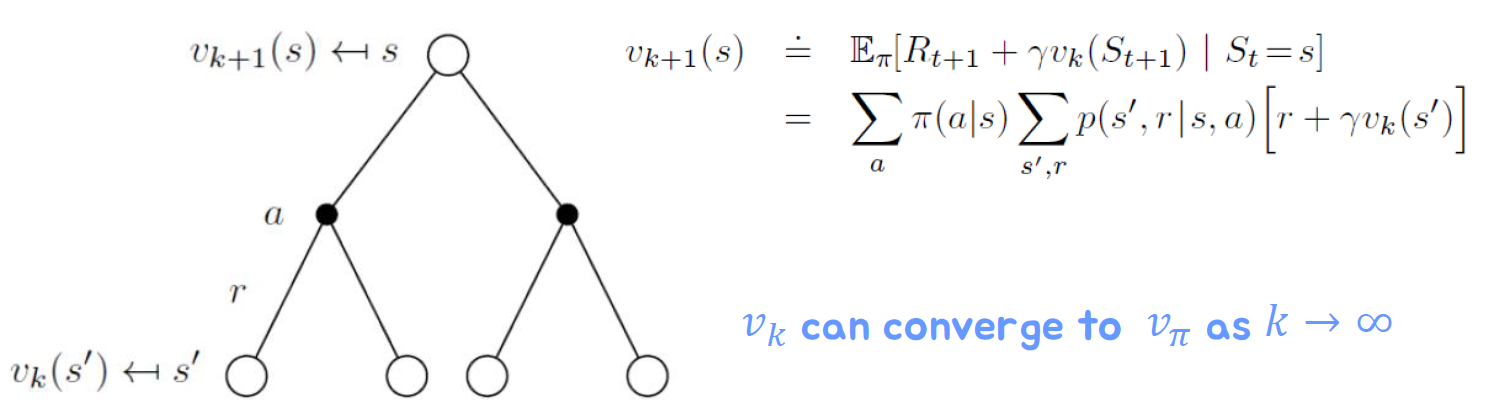
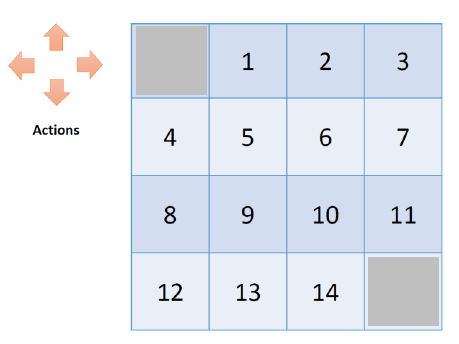
다음 형태의 Small Grid World에 우리가 배웠던 것들을 적용해보자.
• 할인되지 않은 에피소드형 MDP( 𝜸=𝟏)
• 비종단 상태 1, …, 14
• 공유 사각형의 최종 상태
• 그리드 외부로 이어지는 작업은 상태를 변경하지 않고 그대로 둡니다.
• 보상은 모든 움직임에 대해 1입니다.
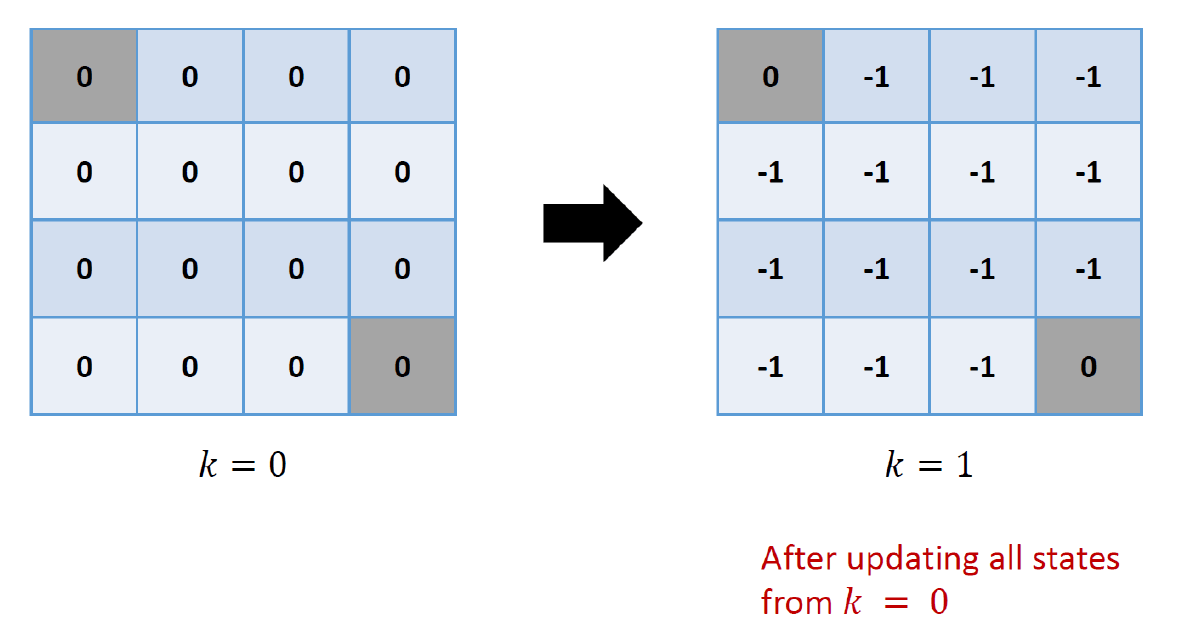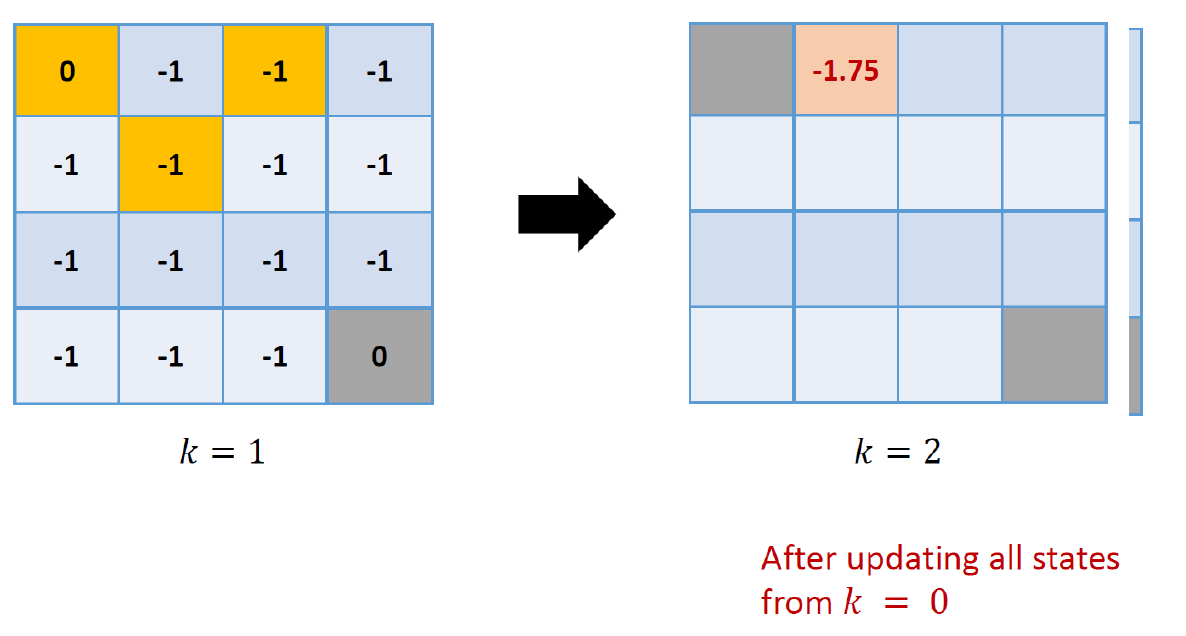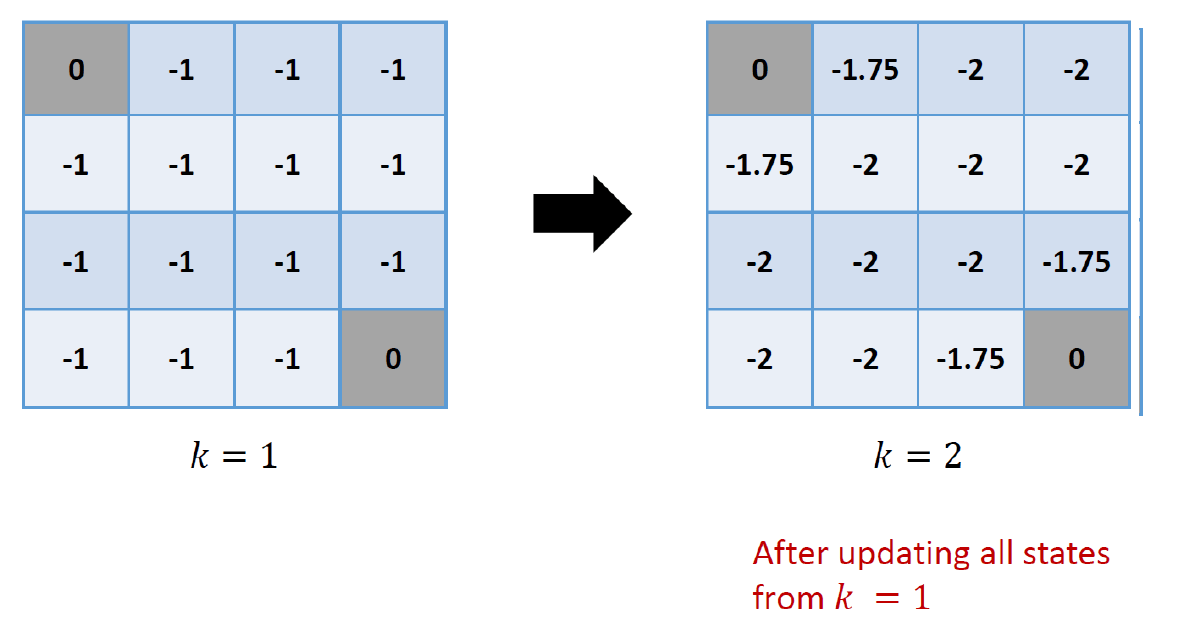
Small Grid World with Random Policy의 에이전트는 균일한 무작위 정책을 따르기 때문에 다음과 같을 것이다.

나온 이유는 다음과 같다.

이를 iterative하게 하나씩 적용하면 다음과 같다.
따라서 다음의 결과를 얻을 수 있다.
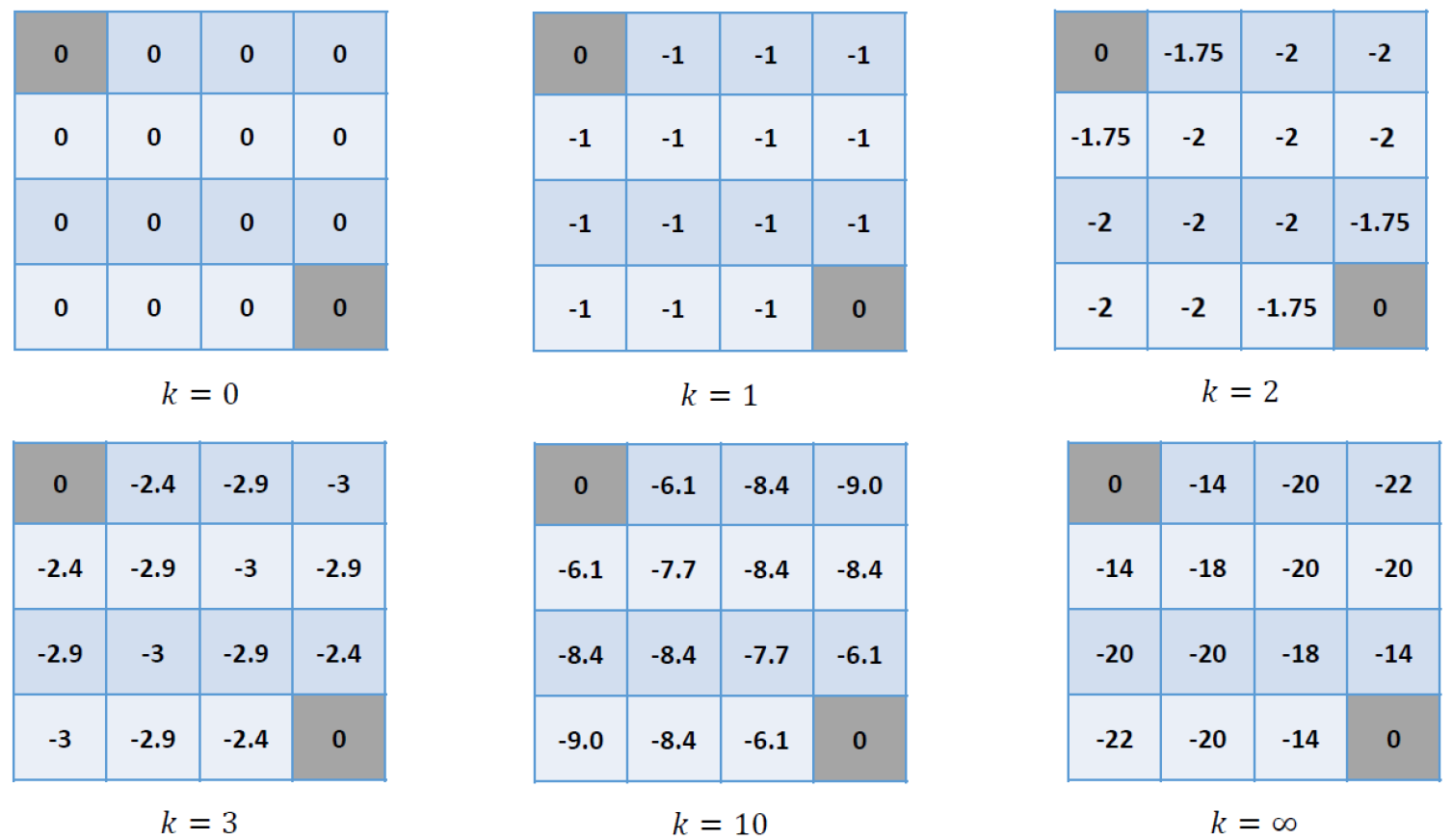
Random이 아닌 Policy로 알고리즘을 작성하면 다음과 같다.

이를 아까의 Random을 대체하면 다음 그림처럼 단계적으로 진행될 것이다.
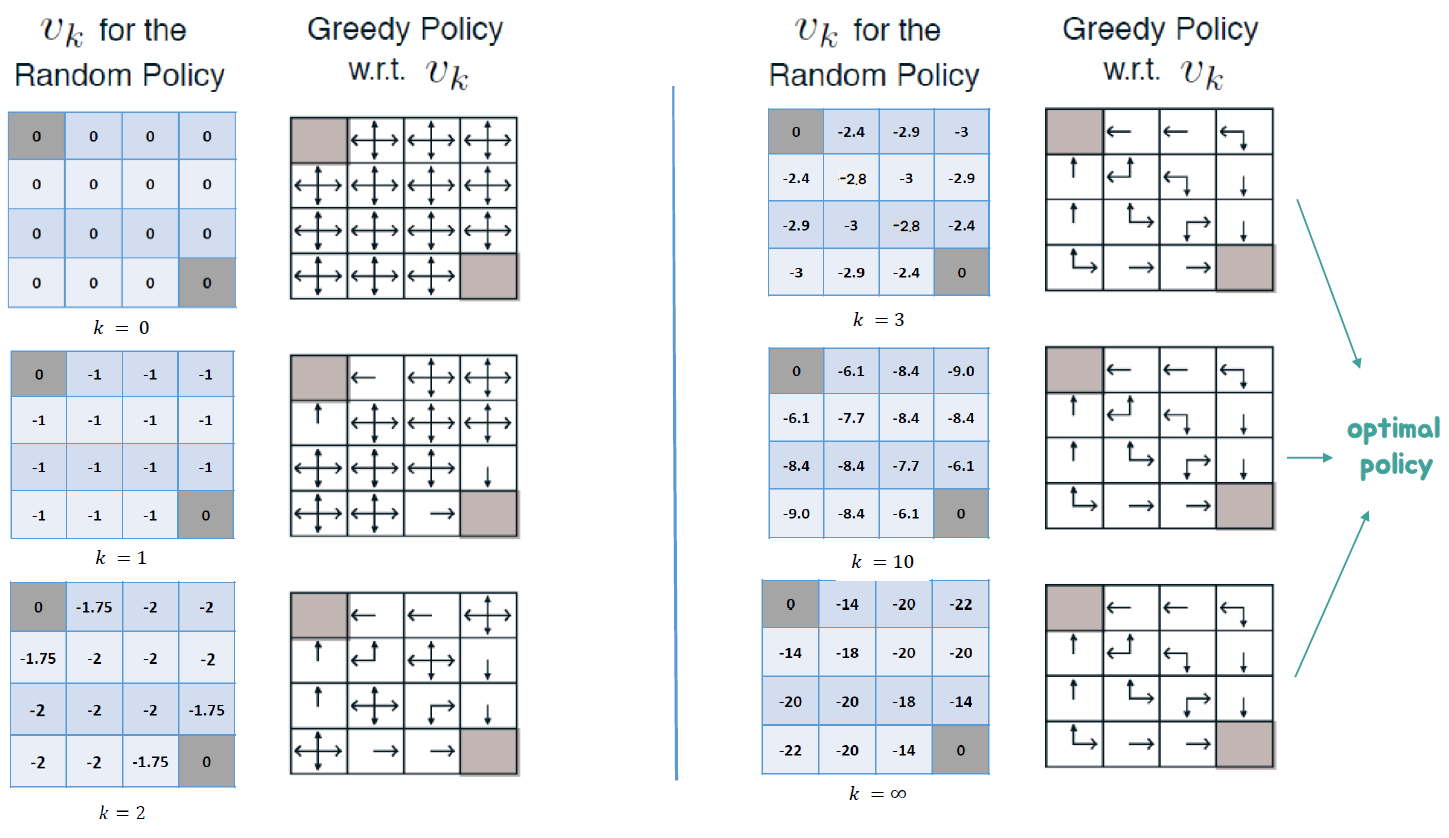
Policy Improvement를 식으로 정리해보자.
Deterministic policy를 𝑎=𝜋(𝑠)로 정의하자. 그렇다면 acting greed에 따라 다음의 식이 나올 것이다.

이는 일정 스탭 s이후 다음과 같이 표현될 수 있다.

따라서 value function을 다음과 같이 작성할 수 있다.

따라서 𝜋는 optimal policy이다.
실제 유도식은 다음과 같다.
Policy Improvement에서 Iteration이 진행되면 간단하게 다음 그림일 것이다.
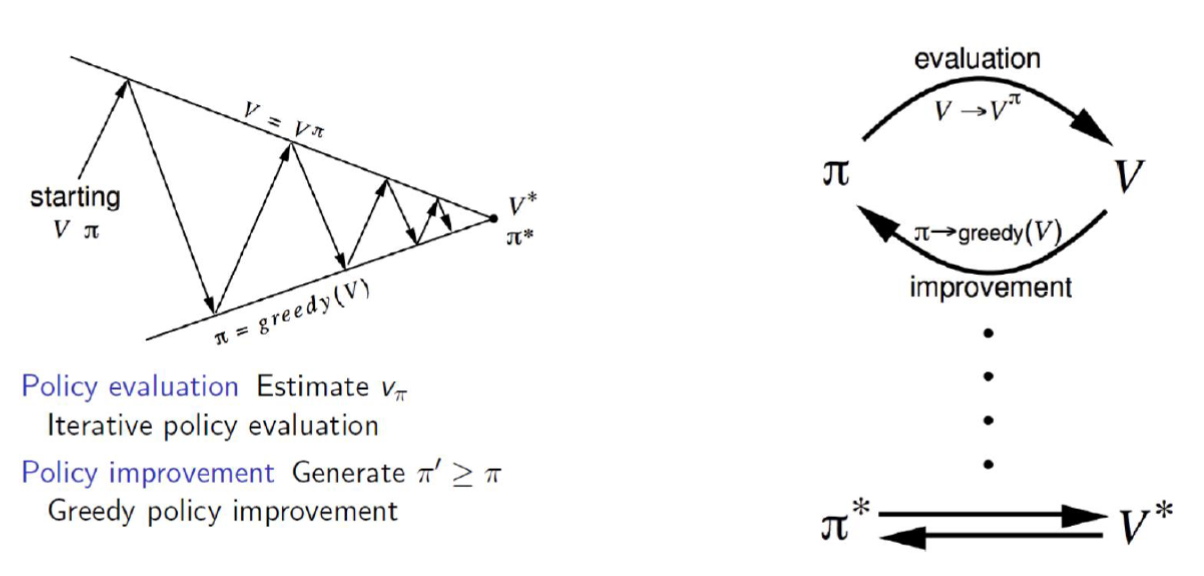
이를 Policy Iteration이라고 명명하면 알고리즘은 다음과 같다.

이를 더 효율성있게 하는 방법은 없을까?
Modified Policy Iteration은 정책 평가와 정책 개선을 번갈아 가면서 수행하는 것은 비효율적이다. 그렇다면 한 번의 가치 평가로 최적 가치 함수에 수렴시키면 효율적이지 않을까? 그렇다면 어떻게 최적 정책을 찾을 수 있을까? 탐색과 exploitation을 적절하게 사용하면 될 것이다! 이게 바로 Value Iteration이다.
Value Iteration은 다음과 같이 표현할 수 있다.


알고리즘은 다음과 같다.

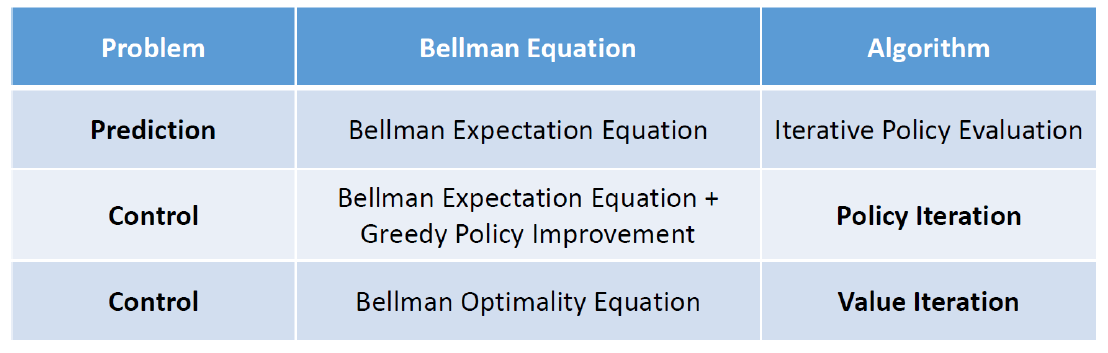
요약하면 다음과 같다.
'강화학습' 카테고리의 다른 글
| Chapter6. Model-Free Control (0) | 2023.05.22 |
|---|---|
| Chapter 5. Model-free Prediction (1) | 2023.05.21 |
| Chapter3. Markov Decision Process (0) | 2023.05.21 |
| Chapter 2 Reinforcement Learning Overview (0) | 2023.05.21 |
| Chapter 1 Introduction (0) | 2023.05.20 |




