우리는 전 chapter에서는 Model-based Planning에 대해서 알아보았다. Model-based Planning(모델 기반 계획)은 주어진 환경 모델을 사용하여 계획을 수립하는 방법이었다. 모델 기반 계획은 환경의 동작을 사전에 알고 있으며, 이를 활용하여 가능한 행동 시퀀스를 시뮬레이션하고 평가하여 최적의 행동 계획을 수립했다. 모델 기반 계획은 환경 모델을 사용하여 미리 상태 전이 확률과 보상 함수를 추정하고, 이를 기반으로 최적의 행동 선택을 수행했다.

이번 chapter에서는 주어진 상태에서의 기대 반환값 또는 가치를 추정하여 에이전트가 어떤 상태에서 얼마나 좋은지를 평가하는 Model-free Prediction에 대해서 알아보자.
Model-free Reinforcement Learning은 true MDP 모델 없이 특정 정책의 예상 reward를 추정한다. 즉, 환경 모델 없이 주어진 환경과 상호작용하면서 최적의 행동을 학습하는 방법이다.
에이전트는 주어진 정책이 얼마나 좋은지를 평가할 수 있는 Model-free prediction은 어떻게 추정될까?
이는 2가지 방식으로 진행된다.
- Monte Carlo Prediction(몬테카를로 예측): 몬테카를로 예측은 실제 에피소드를 통해 주어진 정책을 따라 에이전트가 상태와 보상을 관찰하고, 이를 기반으로 가치 함수를 추정하는 방법입니다. 몬테카를로 예측은 에피소드가 끝날 때까지 관찰된 상태와 보상을 토대로 가치 함수를 업데이트합니다. 이를 통해 각 상태의 기대 반환값을 추정하여 가치 함수를 개선합니다.
- Temporal Difference(TD) Learning: TD 학습은 에피소드가 종료되지 않아도 중간 중간에 관찰된 상태의 보상을 토대로 가치 함수를 업데이트하는 방법입니다. TD 학습은 현재 상태의 보상과 다음 상태의 가치 추정값을 이용하여 가치 함수를 업데이트합니다. 이를 통해 TD 오차(Temporal Difference error)를 최소화하고 가치 함수를 개선합니다.
Monte-Carlo Methods의 정의를 보자.
수치 결과를 얻기 위해 반복되는 임의 샘플링에 의존하는 계산 알고리즘 클래스로 정의된다.
그렇다면 Monte-Carlo를 Reinforcement Learning에서 사용한다면 다음과 같다.
• MC 방법은 경험의 에피소드에서 직접 학습
• MC는 모델이 없음: MDP 전환/보상에 대한 지식 없음
• MC는 전체 에피소드에서 학습 -> 부트스트래핑 없음
• MC는 가능한 가장 간단한 아이디어를 사용: value == mean return
• 에피소드 MDP만 해당(모든 에피소드가 종료되어야 함)
즉, 위에 설명한 1번과 같다.
Monte-Carlo Policy Evaluation은 다음과 같다.
목표는 정책 𝜋에 따른 에피소드 경험을 통해 𝑣𝜋(𝑠)를 학습하는 것이다. 에피소드 경험은 상태 𝑆1, 행동 𝐴1, 보상 𝑅2, ..., 상태 𝑆𝑘을 𝜋에 따라 무작위로 선택하여 얻는 것이다.
리턴은 총 감가된 보상을 나타내며, 𝑅𝑡+1, 𝑅𝑡+2, ..., 𝑅𝑇을 𝛾로 감가하여 계산한다. 𝛾는 할인율로, 미래의 보상에 대한 중요도를 조절한다.
가치 함수는 상태 𝑠에서의 기대 리턴을 나타내며, 에피소드를 진행하면서 각 상태에서의 리턴을 측정하고 평균을 구한다. 이를 통해 가치 함수를 추청한다
몬테카를로 정책 평가는 기대 리턴 대신 경험적인 평균 리턴을 사용한다. 즉, 여러 번의 에피소드를 진행하면서 각 에피소드에서 얻은 리턴을 모두 더하고 에피소드 수로 나누어 평균을 구한다. 이렇게 구한 평균 리턴을 통해 가치 함수를 추청한다.
몬테카를로 정책 평가는 환경 모델에 대한 사전 지식이 필요하지 않으며, 주어진 정책에 따라 에피소드를 플레이하면서 가치 함수를 추정하는 강력한 방법이다.
First-Visit Monte-Carlo Policy Evaluation은 특정 상태 𝑠를 평가하는 방법이다. 이 방법은 에피소드 동안 상태 𝑠가 처음으로 방문된 시점인 𝑡를 찾습니다.
각 상태는 해당 상태를 방문한 횟수를 나타내는 카운터 𝑁(𝑠)를 가지고 있다. 따라서 𝑁𝑠를 1 증가시킨다. 동시에 상태 𝑠에서 발생한 총 리턴을 나타내는 S𝑠에 현재 리턴을 더 한다.
가치 함수는 해당 상태의 평균 리턴으로 추정된다. 따라서 𝑉(𝑠)는 S(𝑠)를 𝑁(𝑠)로 나눈 값으로 계산된다. 이를 통해 가치 함수를 추정할 수 있다.
First-Visit Monte-Carlo Policy Evaluation은 상태 𝑠가 에피소드 동안 처음 방문된 시점인 𝑡를 찾고, 이를 기반으로 해당 상태의 가치를 추정한다. 큰 수의 법칙에 따라 𝑁(𝑠)가 무한히 커질수록 𝑉(𝑠)는 𝑣𝜋(𝑠)로 수렴하게 된다.
이 방법은 각 상태의 방문 횟수와 리턴을 추적하여 정확한 가치 함수 추정을 가능하게 한다.
따라서 이를 Every-Visit Monte-Carlo Policy Evaluation에 그대로 적용할 수 있다.
Mars Rover라는 예제를 통해 이를 적용해보자.
"Mars Rover" 예제에서는 우리가 상태 전이 확률 𝑃(𝑆′|𝑆,𝐴)과 같은 모델에 대한 정보를 알지 못한다. 정책은 모든 상태에서 "왼쪽으로 이동"만 하는 것이며, 보상은 이동할 때마다 -1이 주어지고, S1에 도착하면 +1이 주어진다. 할인율은 𝛾=0.5로 설정된다.

First-Visit MC의 경우, 샘플 에피소드는 다음과 같다:
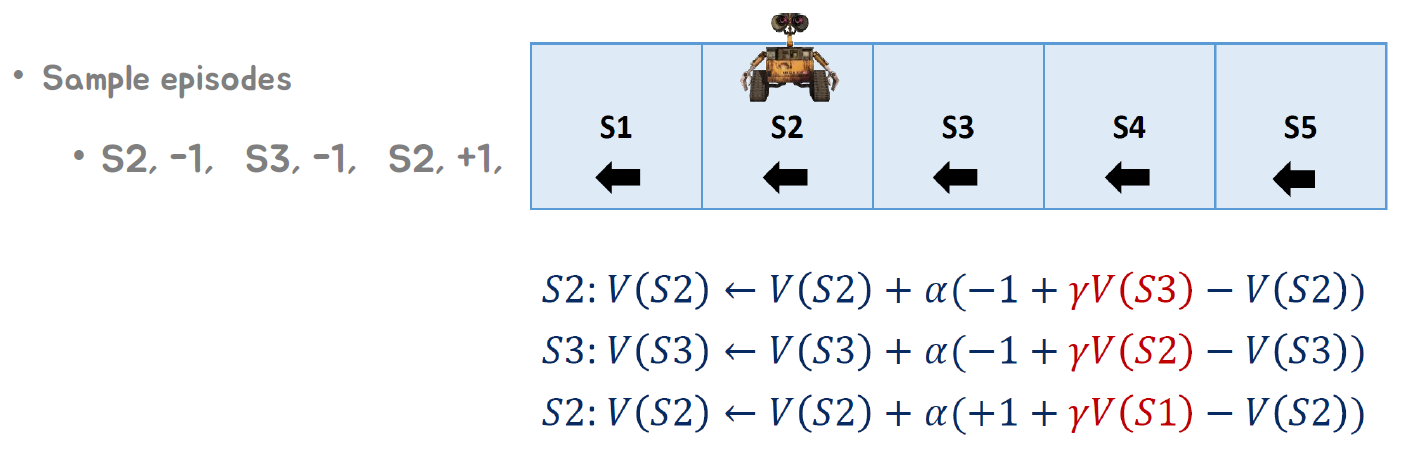
• 에피소드 1: S2, -1, S3, -1, S2, +1, S1
• 에피소드 2: S2, +1, S1

Every-Visit MC의 경우, 샘플 에피소드는 다음과 같다:
• 에피소드 1: S2, -1, S3, -1, S2, +1, S1
• 에피소드 2: S2, +1, S1
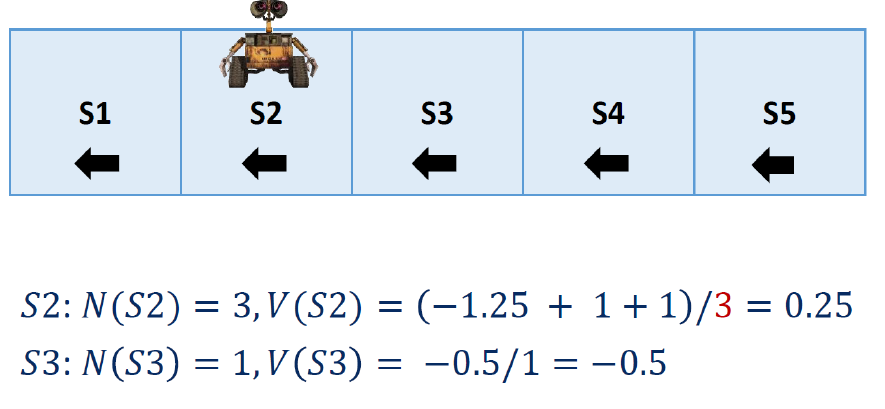
이 예제에서는 우리가 상태 전이 확률을 알지 못하기 때문에 Monte Carlo 방법을 사용하여 가치 함수를 추정한다. First-Visit MC와 Every-Visit MC는 모든 에피소드에서 각 상태의 방문 횟수와 리턴을 추적하여 가치 함수를 추정한다.
First-Visit MC의 경우, 각 상태가 첫 번째 방문된 시점에서 리턴을 계산하고, 그에 따라 가치 함수를 업데이트 한다. 에피소드 1에서는 S2, S3, S2, S1이 첫 번째 방문된 상태이다.
Every-Visit MC의 경우, 모든 방문 시점에서 상태의 방문 횟수와 리턴을 추적하여 가치 함수를 추정한다. 따라서 에피소드 1과 에피소드 2에서 S2와 S1이 여러 번 방문된 상태이다.
이렇게 에피소드를 통해 First-Visit MC와 Every-Visit MC를 활용하여 가치 함수를 추정할 수 있다.
Incremental Monte-Carlo Update는 에피소드가 종료된 후 𝑆1,𝐴1,𝑅2,…,𝑆𝑘~𝜋와 같은 에피소드를 기반으로 가치 함수를 점진적으로 업데이트하는 방법이다.
각 상태 𝑆𝑡에 대해 해당 상태의 리턴 𝐺𝑡을 이용하여 가치 함수를 업데이트한다. 𝑁(𝑆𝑡)는 해당 상태를 방문한 횟수를 나타내는 카운터로, 𝑁(𝑆𝑡)를 1 증가시킵니다. 그리고 𝑉(𝑆𝑡)를 현재의 가치 함수 값에서 다음과 같이 업데이트합니다:
𝑉(𝑆𝑡)←𝑉(𝑆𝑡)+(1/𝑁(𝑆𝑡))(𝐺𝑡−𝑉(𝑆𝑡)).
또한, 비정상적인(non-stationary) 문제의 경우, 진행되는 평균을 추적하는 것이 유용할 수 있다. 𝑉(𝑆𝑡)를 다음과 같이 업데이트하여 이전 데이터를 잊어버리지 않고 가치 함수를 추정한다: 𝑉(𝑆𝑡)←𝑉(𝑆𝑡)+𝛼(𝐺𝑡−𝑉(𝑆𝑡)).
여기서 𝛼는 학습률을 나타내며, 1/𝑁(𝑆)보다 큰 값을 설정하면 이전 데이터를 빠르게 잊어버릴 수 있다. 이를 통해 최신 데이터에 더 많은 중요성을 부여하여 가치 함수를 업데이트할 수 있다.
Incremental Monte-Carlo Update는 에피소드가 종료된 후에 각 상태의 리턴을 이용하여 가치 함수를 점진적으로 업데이트하는 강력한 방법이다.
Temporal-Difference Learning은 에피소드 경험을 통해 직접 학습하는 방법이다. TD 방법은 모델의 전이 확률이나 보상에 대한 사전 지식 없이 진행된다.
TD 방법은 불완전한 에피소드로부터 학습을 진행하며, 부트스트래핑(bootstrapping)을 통해 학습한다. 부트스트래핑은 현재 추정값을 이용해 추정값을 업데이트하는 것을 의미한다.
TD 방법은 "추측을 추측으로부터 업데이트한다"는 특징을 가지고 있다. 즉, 현재 추정값을 다음 추정값으로 업데이트합니다. 이를 통해 TD 방법은 불완전한 에피소드에서도 학습이 가능하다.
"Temporal-Difference Learning"은 모델의 전이 확률이나 보상에 대한 사전 지식이 없이도 직접 학습하는 강력한 방법이다.
Monte Carlo vs. Temporal Difference
Monte Carlo와 Temporal Difference는 모두 정책 𝜋에 따른 에피소드 경험을 통해 가치 함수 𝑣𝜋(𝑠)를 학습하는 방법이다.
Monte Carlo 방법에서는 인크리멘털 모델로 업데이트하는 방식을 사용한다. 즉, 𝑉(𝑆𝑡)를 다음과 같이 업데이트한다: 𝑉𝑆𝑡←𝑉𝑆𝑡+𝛼(𝐺𝑡−𝑉𝑆𝑡).
여기서 𝛼는 학습률을 의미한다. Monte Carlo 방법은 에피소드가 끝나야 전체 리턴을 계산하고 가치 함수를 업데이트한다.
반면 Temporal Difference 방법은 TD 학습 알고리즘을 사용한다. 가치 함수를 추정하기 위해 𝑅(𝑡+1)+𝛾𝑉(𝑆𝑡+1)을 추정값으로 설정하여 𝑉(𝑆𝑡)를 다음과 같이 업데이트한다: 𝑉(𝑆𝑡)←𝑉(𝑆𝑡)+𝛼(𝑅(𝑡+1)+𝛾𝑉(𝑆𝑡+1)−𝑉(𝑆𝑡)). 여기서 𝑅(𝑡+1)+𝛾𝑉(𝑆𝑡+1)을 TD 타겟(TD target)이라고 부릅니다. 또한, 𝑅(𝑡+1)+𝛾𝑉(𝑆𝑡+1)−𝑉(𝑆𝑡)는 TD 오차(TD error)라고 부릅니다.
Monte Carlo 방법은 에피소드가 끝날 때까지 기다려야 전체 리턴을 계산하여 가치 함수를 업데이트합니다. 반면 Temporal Difference 방법은 에피소드 중간에도 가치 함수를 업데이트하며, 추정값을 기반으로 현재 가치를 업데이트합니다.
Example : TD Policy Evaluation
Driving Home Example


즉, MC와 TD를 비교하면 다음과 같다.
Monte Carlo 방법은 완전한 시퀀스에서만 학습할 수 있다. 즉, 에피소드가 종료될 때까지 기다려야 전체 리턴을 계산하고 가치 함수를 업데이트한다. 또한, Monte Carlo 방법은 에피소드가 종결되는 환경에서만 동작한다.
반면 Temporal Difference 방법은 불완전한 시퀀스에서도 학습이 가능하다. 에피소드 중간에도 가치 함수를 업데이트할 수 있으며, 최종 결과를 알기 전에도 학습이 가능하다. Temporal Difference 방법은 한 번의 스텝이 끝날 때마다 온라인으로 학습할 수 있다. 또한, Temporal Difference 방법은 종료되지 않는 환경에서도 동작한다.
Monte Carlo 방법은 에피소드의 완전한 결과를 기다려야하고, TD 방법은 에피소드 중간에도 학습이 가능하며 온라인으로 업데이트할 수 있기 때문에 더 빠르게 학습할 수 있다. 또한, TD 방법은 종료되지 않는 환경에서도 적용 가능하므로 더 넓은 범위의 문제에 적용할 수 있다.
Bias/Variance Trade-Off
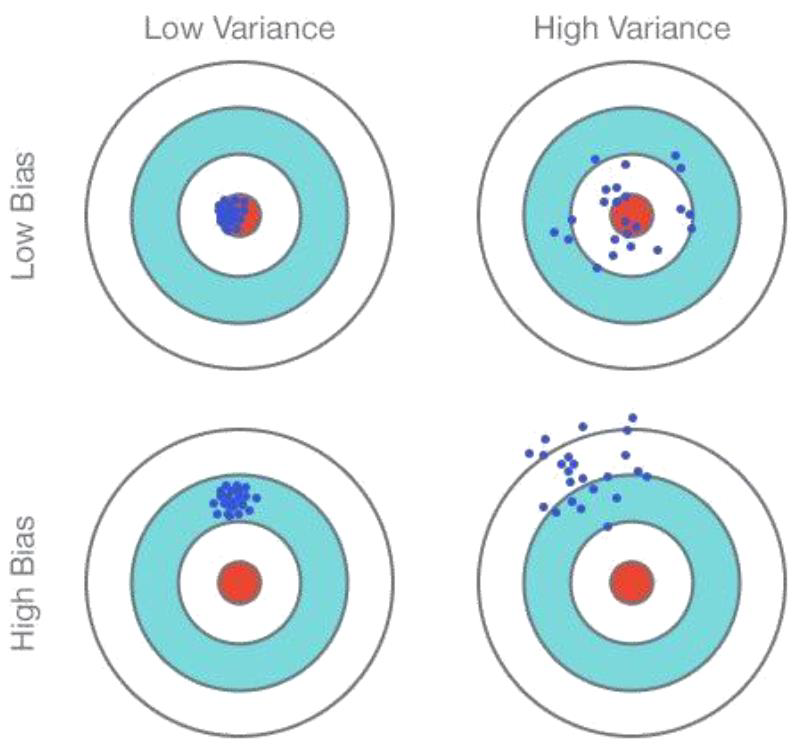
"Bias"는 학습 알고리즘에서 잘못된 가정으로 인한 오차를 의미한다. 즉, 학습 알고리즘이 잘못된 가정을 하여 발생하는 오차이다.
"Variance"는 학습 데이터의 작은 변동에 민감하여 발생하는 오차를 의미한다. 즉, 학습 데이터의 작은 변화에도 모델의 예측이 크게 영향을 받는 것을 말한다.
Return 𝐺𝑡=𝑅(𝑡+1)+𝛾𝑅(𝑡+2)+...은 𝑣𝜋(𝑠𝑡)의 무편향(unbiased) 추정치다. 즉, 이는 𝑣𝜋(𝑠𝑡)를 정확하게 추정하는 경향이 있다.
실제 TD 타겟은 𝑣𝜋(𝑠𝑡)의 무편향 추정치다. 하지만 보통 TD 타겟은 𝑣𝜋(𝑠𝑡)의 불완전한(biased) 추정치다. 즉, TD 타겟은 정확한 추정치가 아닐 수 있다.
하지만 TD 타겟은 리턴에 비해 분산이 훨씬 낮다. 즉, TD 타겟은 학습 데이터의 작은 변동에 덜 민감하며, 더 일반화된 예측을 할 수 있다.
MC vs. TD variance와 bias에 대해서 비교해보자
Monte Carlo 방법은 분산이 높지만 편향이 없다. 즉, Monte Carlo 방법은 많은 변동성을 가지지만 추정치의 편향은 없다. Monte Carlo 방법은 좋은 수렴 성질을 가지고 있으며, 함수 근사화와 함께 사용되더라도 잘 수렴한다. 초기값에 대한 민감도도 낮다. 또한, 이해하고 사용하기 매우 간단하다.
Temporal Difference 방법은 분산이 낮지만 약간의 편향이 있을 수 있다. 일반적으로 Monte Carlo 방법보다 효율적이다. Temporal Difference 방법은 𝑣𝜋𝑠에 수렴하지만 함수 근사화와 함께 사용할 때 항상 수렴하지는 않을 수 있다. 초기값에 대해 민감도가 더 높다.
즉, Monte Carlo 방법은 분산이 높기 때문에 변동이 크지만, 편향이 없기 때문에 추정치가 일반화된 예측을 할 수 있다. 반면 Temporal Difference 방법은 분산이 낮고 편향이 있는 편이므로 더 효율적이지만 초기값에 더 민감할 수 있다.
Batch MC and TD
Batch MC and TD는 유한한 데이터셋에 대한 배치(오프라인) 솔루션이다. 주어진 K개의 에피소드 집합이 있을 때, 반복적으로 𝑘∈[1,𝐾] 범위에서 에피소드를 샘플링하고, 해당 샘플링된 에피소드에 대해 MC 또는 TD를 적용한다.
MC(Monte Carlo)와 TD(Temporal Difference)는 어떤 값에 수렴하게 될까?
MC는 에피소드 전체를 기반으로 가치 함수를 추정하는 방법이므로, Batch MC는 주어진 데이터셋에 대해 에피소드마다 가치 함수를 추정한 후 평균을 취한다. 따라서 Batch MC는 주어진 데이터셋에 대해 가치 함수를 추정하는데 수렴하게 된다.
TD는 한 스텝씩 진행하면서 가치 함수를 업데이트하는 방법이므로, Batch TD는 주어진 데이터셋에 대해 각 스텝에서의 TD 업데이트를 적용한다. 따라서 Batch TD는 주어진 데이터셋에 대해 가치 함수를 추정하는데 수렴하게 된다.
AB Example
AB 예제에서는 두 개의 상태 𝐴와 𝐵가 있으며 할인율(𝛾)은 1로 설정됩니다. 주어진 8개의 에피소드 경험은 다음과 같다:
• 에피소드 1: 𝐴,0,𝐵,0
• 에피소드 2: 𝐵,1
• 에피소드 3: 𝐵,1
• 에피소드 4: 𝐵,1
• 에피소드 5: 𝐵,0
• 에피소드 6: 𝐵,1
• 에피소드 7: 𝐵,1
• 에피소드 8: 𝐵,1

주어진 에피소드에서 𝐴와 𝐵의 가치 함수 𝑉(𝐴)과 𝑉(𝐵)을 추정해보겠습니다.
먼저, MC(Monte Carlo) 방법을 사용하여 가치 함수를 추정하면 다음과 같습니다:
• 𝑉(𝐴) = (0 + 0) / 2 = 0
• 𝑉(𝐵) = (1 + 1 + 1 + 0 + 1 + 1 + 1 + 1) / 8 = 0.875
다음으로, TD(Temporal Difference) 방법을 사용하여 가치 함수를 추정하면 다음과 같습니다:
• 𝑉(𝐴) = 0 + 1 = 1
• 𝑉(𝐵) = 1 + 0.875 = 1.875
따라서, 주어진 8개의 에피소드에서 𝐴의 가치 함수는 0 또는 1로, 𝐵의 가치 함수는 0.875 또는 1.875로 추정됩니다.
추가적으로 사용시 MC(Monte Carlo)와 TD(Temporal Difference) 방법의 차이점을 알아보자.
가장 간단한 TD 방법에서는 (𝑠,𝑎,𝑟,𝑠′)를 사용하여 𝑉(𝑠)를 업데이트합니다. 즉, 𝑉(𝑠)를 업데이트하는 데에는 𝑂(1)의 연산이 필요합니다. 에피소드의 길이가 𝐿인 경우에도 𝑂(𝐿)의 연산이 필요합니다.
반면 MC 방법에서는 에피소드가 끝날 때까지 기다려야하며, 이때도 업데이트에는 𝑂(𝐿)의 연산이 필요합니다.
TD 방법은 Markov 구조를 활용합니다. 즉, (𝑠,𝑎,𝑟,𝑠′)의 정보를 활용하여 가치 함수를 업데이트합니다. Markov 도메인에서 이러한 구조를 활용하는 것이 도움이 됩니다.
반면 MC 방법은 Markov 속성을 활용하지 않습니다. 따라서 비-Markov 환경에서는 보통 MC 방법이 더 효과적입니다.
결론적으로, TD 방법은 𝑂(1)의 연산으로 가치 함수를 업데이트하며 Markov 구조를 활용합니다. 반면 MC 방법은 에피소드의 종료까지 기다려야하며 Markov 속성을 활용하지 않습니다. 따라서 비-Markov 환경에서는 MC 방법이 일반적으로 더 효과적입니다.
DP vs. MC vs. TD
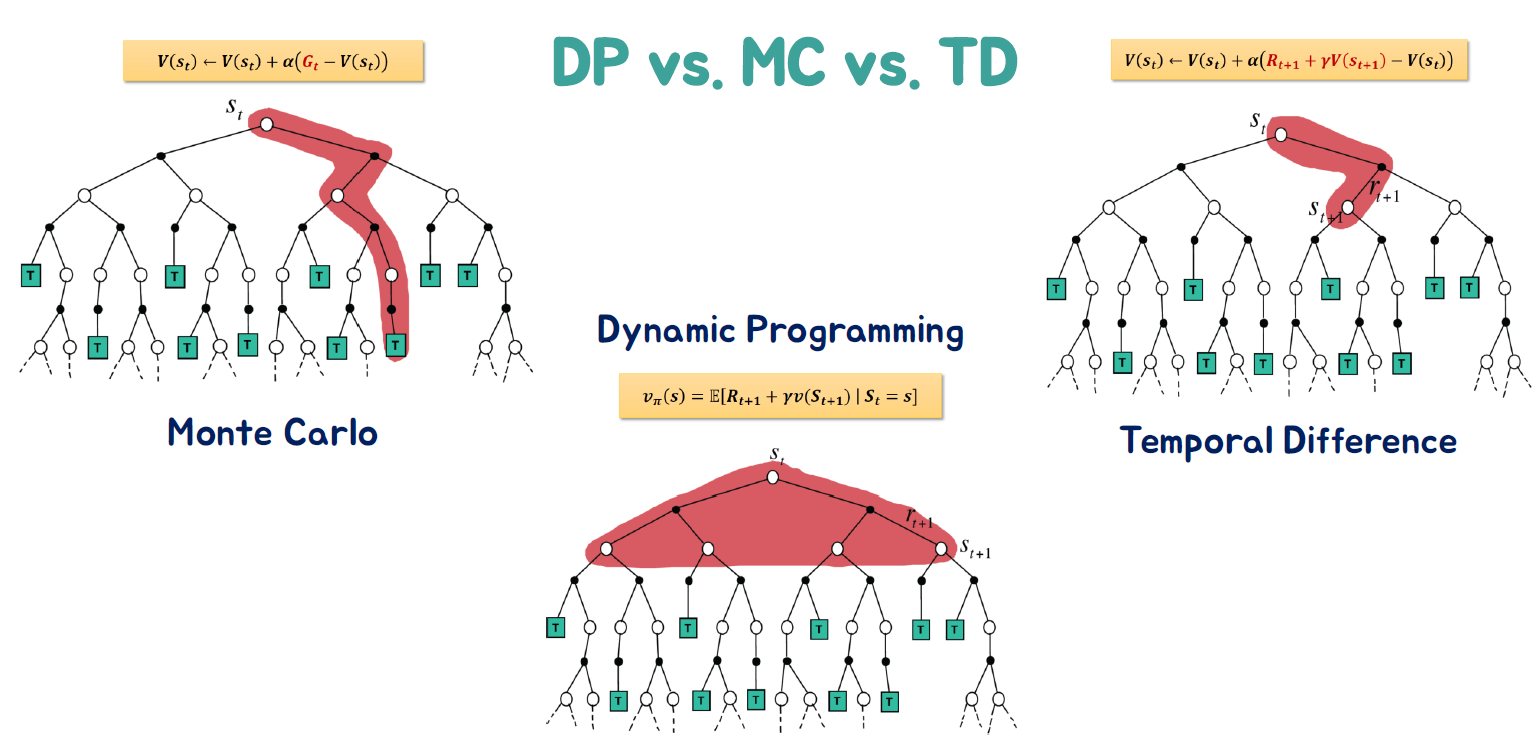
Sampling and Bootstrapping
"Sampling"은 에피소드 경험에서 정보를 수집하는 것을 의미합니다. 동적 계획법(DP)은 샘플링하지 않고 모든 가능한 상태와 행동을 고려하여 문제를 해결합니다. 반면에 Monte Carlo(MC)와 Temporal Difference(TD) 방법은 에피소드를 샘플링하여 정보를 수집합니다.
"Bootstrapping"은 다른 추정치를 기반으로 추정치를 업데이트하는 것을 의미합니다. 동적 계획법은 부트스트래핑을 사용하여 추정치를 업데이트합니다. 즉, 현재 추정치를 기반으로 다른 추정치를 계산하고 업데이트합니다. 반면에 Monte Carlo 방법은 부트스트래핑을 사용하지 않고, 에피소드가 종료될 때까지 기다려야 전체 리턴을 계산하여 추정치를 업데이트합니다. 마찬가지로 Temporal Difference 방법은 추정치를 업데이트할 때 부트스트래핑을 사용합니다.
간단히 말하면, Sampling은 에피소드 경험에서 정보를 수집하는 것이고, Bootstrapping은 추정치를 다른 추정치로 업데이트하는 것입니다. 동적 계획법은 샘플링하지 않고 부트스트래핑을 사용하며, Monte Carlo와 Temporal Difference 방법은 샘플링과 부트스트래핑을 각각 사용합니다.
Blackjack Example (https://gym.openai.com/envs/Blackjack-v0/)
Blackjack 예제에서는 다음과 같은 상태와 행동을 가지고 있습니다.
상태 (총 280개):
현재 카드의 합계 (4~21)
딜러가 보여주는 카드 (에이스~10)
"사용 가능한" 에이스가 있는지 여부 (예 또는 아니오)
행동:
stick: 카드를 더이상 받지 않고 게임을 종료합니다.
hit: 추가 카드를 받습니다. (교체 없이)
전이 (Transitions): 카드의 합계가 12 미만인 경우 자동으로 hit 행동이 선택됩니다.
stick에 대한 보상:
카드의 합계가 딜러의 카드 합계보다 큰 경우: +1
카드의 합계가 딜러의 카드 합계와 같은 경우: 0
카드의 합계가 딜러의 카드 합계보다 작은 경우: -1
hit에 대한 보상:
카드의 합계가 21을 초과하는 경우: -1 (게임 종료)
그 외의 경우: 0
이러한 설정으로 Blackjack 예제에서 게임이 진행됩니다.
Blackjack Value Function after Prediction

𝑛-Step Prediction
𝑛-Step Prediction은 TD 타겟이 미래로 𝑛스텝을 바라보도록 하는 것을 의미합니다.
일반적으로 TD(Temporal Difference) 학습에서는 TD 타겟을 현재 보상과 다음 상태의 가치 함수를 이용하여 업데이트합니다. 하지만 𝑛-Step Prediction에서는 TD 타겟이 더 멀리 미래의 보상과 상태의 가치 함수를 고려하여 업데이트합니다. 즉, 𝑛스텝만큼 미래로 전진하여 TD 타겟을 계산합니다.
예를 들어, 𝑛=2로 설정한 경우, TD 타겟은 현재 보상과 현재 상태에서 2스텝 후의 보상과 상태의 가치 함수를 고려하여 계산됩니다. 이를 통해 미래의 정보를 좀 더 포함한 업데이트를 수행할 수 있습니다.
𝑛-Step Prediction은 𝑛의 값을 조정함으로써 현재와 멀리 미래의 정보를 얼마나 고려할지 조절할 수 있습니다. 작은 𝑛값은 즉각적인 보상에 더 중점을 두며, 큰 𝑛값은 장기적인 보상을 고려합니다.
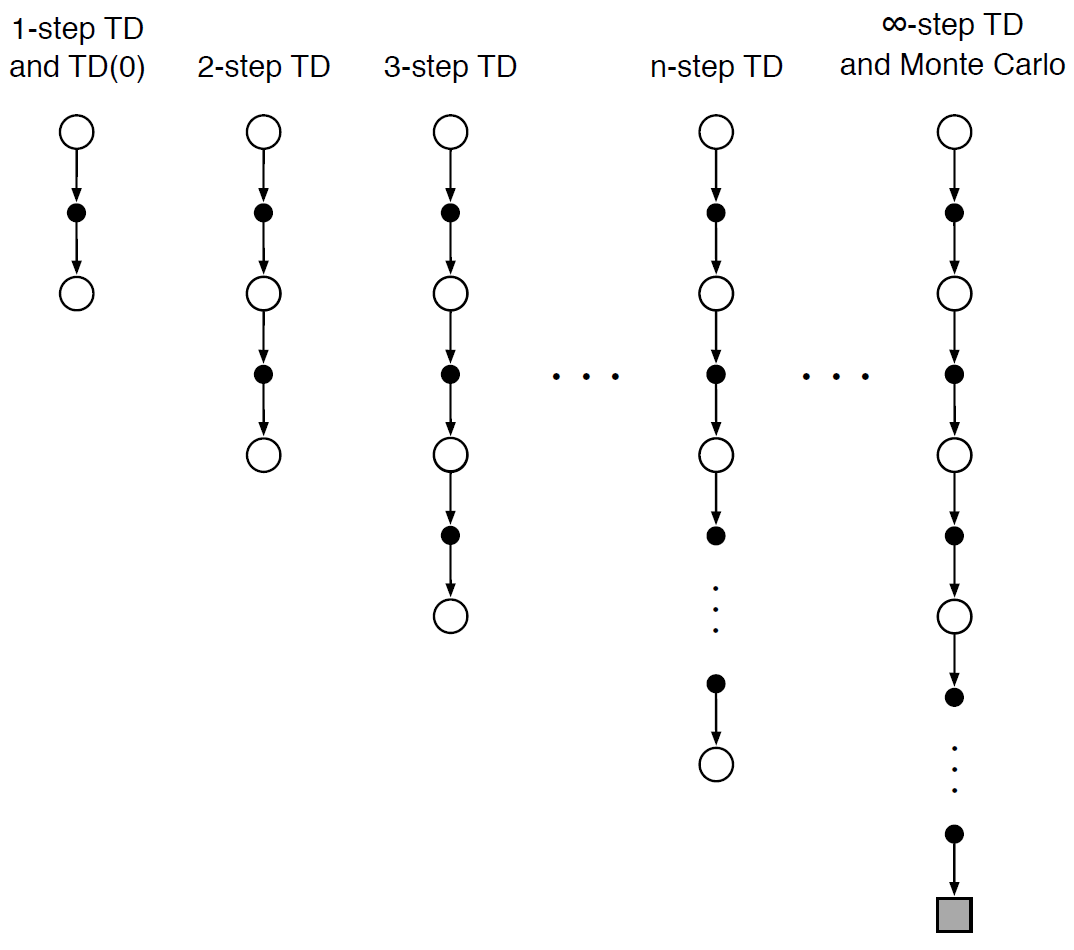
𝑛-Step Return
𝑛-Step Return은 𝑛=1,2,..∞에 대한 다음과 같은 n-스텝 리턴을 고려합니다:

n-스텝 리턴을 정의합니다. n-스텝 리턴은 현재 시점에서부터 n스텝 뒤까지의 리턴을 의미합니다. 즉, 현재 시점에서부터 n스텝 동안의 보상들을 합산한 값입니다. 이를 통해 현재 시점에서부터 n스텝 후의 리턴을 추정할 수 있습니다.

n-스텝 Temporal-Difference(TD) 학습은 n-스텝 리턴을 이용하여 TD 타겟을 업데이트합니다. TD 타겟은 현재 보상과 현재 상태에서부터 n스텝 후의 상태의 가치 함수를 고려하여 계산됩니다. 이를 통해 현재 시점에서부터 n스텝 후의 가치를 추정하고, 이를 이용하여 TD 학습을 수행합니다.

𝑛-Step Return은 𝑛의 값을 조정함으로써 현재와 멀리 미래의 정보를 얼마나 고려할지 조절할 수 있습니다. 작은 𝑛값은 즉각적인 보상에 더 중점을 두며, 큰 𝑛값은 장기적인 보상을 고려합니다.

Averaging 𝑛-Step Returns
우리는 서로 다른 𝑛에 대한 𝑛-스텝 리턴들을 평균화할 수 있습니다. 예를 들어, 2-스텝과 4-스텝 리턴을 평균화할 수 있습니다. 이를 통해 두 가지 다른 시간 단계의 정보를 결합할 수 있습니다. 즉, 2-스텝과 4-스텝 리턴의 평균값을 계산하여 정보를 결합합니다.
그렇다면 모든 시간 단계의 정보를 효과적으로 결합할 수 있을까요? 이는 경우에 따라 다를 수 있습니다. 모든 시간 단계의 리턴을 효과적으로 결합하기 위해서는 과거에서부터 현재까지의 모든 시간 단계를 고려해야 합니다. 이는 연산량이 매우 많아질 수 있습니다. 따라서 모든 시간 단계의 정보를 효율적으로 결합하는 것은 어려울 수 있습니다.
그러나 𝑛-스텝 리턴을 평균화하는 것은 두 개의 시간 단계를 결합하는 방법으로, 상대적으로 계산량이 적은 방법입니다. 따라서 보통은 일부 시간 단계에 대한 평균 리턴을 사용하여 정보를 결합합니다.
𝝀-return
𝝀-리턴은 TD(𝜆) 방법의 한 종류로, 𝜆 값에 따라 𝑛-스텝 업데이트를 평균화하는 방식입니다. 𝜆 값을 [0, 1] 범위에서 선택하며, 각각의 업데이트는 𝜆𝑛−1에 비례하여 가중치를 가지게 됩니다.
𝝀-리턴은 다음과 같이 계산됩니다:
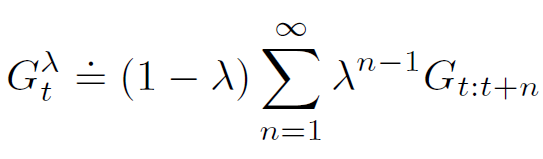
여기서, 𝐺𝑡는 𝑛-스텝 리턴이고, 𝑔𝑡+1은 𝑡+1 시점에서의 가치 추정치입니다.
𝝀-리턴을 이용한 백업은 다음과 같이 수행됩니다:

이를 통해 현재 상태 𝑠에서의 가치 함수 추정치를 𝝀-리턴을 활용하여 업데이트합니다. 𝛼는 학습률을 의미하며, 업데이트의 크기를 조절하는 역할을 합니다.
𝝀-리턴은 𝜆 값에 따라 즉각적인 리턴과 장기적인 리턴을 조절할 수 있습니다. 𝜆 값을 0에 가까워지게 설정하면 즉각적인 리턴에 가중치를 두고, 1에 가까워지게 설정하면 장기적인 리턴에 가중치를 둘 수 있습니다.
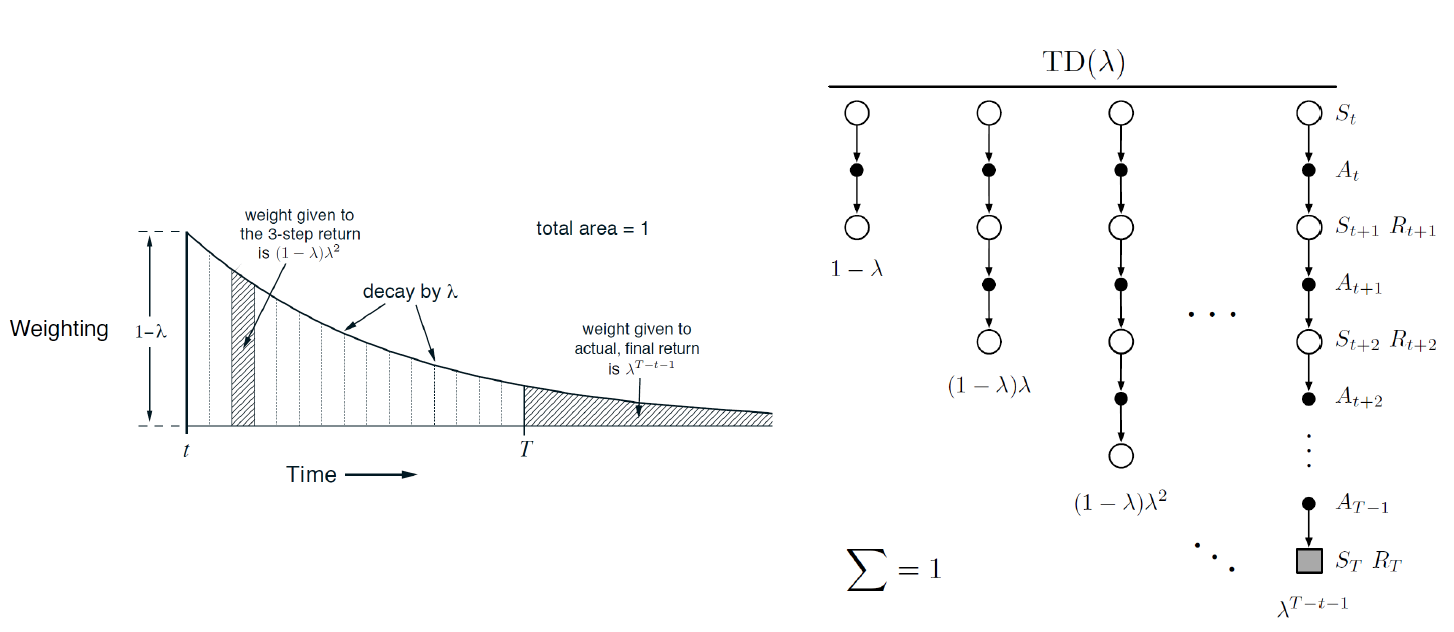
Relation to TD and MC
𝜆-리턴에서 𝜆 값을 조절함에 따라 다음과 같은 관계가 있습니다:
만약 𝜆=0이라면, 𝜆-리턴은 한 단계 TD(0)와 동일해집니다. 즉, 현재 상태에서 바로 다음 상태로의 리턴을 계산하여 업데이트합니다. 이는 한 단계 TD(0) 방법과 같은 방식으로 동작합니다.
반대로, 𝜆=1이라면, 𝜆-리턴은 MC와 동일해집니다. 즉, 전체 에피소드를 통해 리턴을 계산하고 업데이트합니다. MC는 모든 에피소드가 종료될 때까지 기다려야하고, 에피소드가 종료된 후에 업데이트를 수행합니다.

따라서 𝜆 값을 조절함으로써 𝜆-리턴은 TD와 MC 사이의 중간 방법으로 작동합니다. 𝜆 값을 0에 가깝게 설정하면 한 단계 TD(0)에 가까워지고, 1에 가깝게 설정하면 MC에 가까워집니다.
Forward-view TD(𝝀)

Forward-view TD(𝝀)는 𝝀-리턴을 기준으로 가치 함수를 업데이트하는 방법입니다. Forward-view는 미래를 바라보며 𝐺𝑡𝝀를 계산합니다. 따라서, MC와 마찬가지로 완전한 에피소드에서만 계산할 수 있습니다.
Forward-view TD(𝝀)는 다음과 같은 방식으로 가치 함수를 업데이트합니다. 𝝀-리턴인 𝐺𝑡𝝀를 이용하여 가치 함수를 계산한 후, 현재 가치 함수와의 차이를 학습률을 곱하여 업데이트합니다.
𝑉𝑠𝑡 = 𝑉𝑠𝑡 + 𝛼(𝐺𝑡𝝀 - 𝑉𝑠𝑡)
Forward-view TD(𝝀)는 MC와 유사한 방식으로 동작하지만, 𝝀-리턴을 사용하여 가치 함수를 업데이트한다는 점에서 차이가 있습니다. 따라서, 완전한 에피소드가 필요하며, 에피소드가 종료된 후에 업데이트를 수행해야 합니다.

'강화학습' 카테고리의 다른 글
| Chapter 7. Value Function Approximation (0) | 2023.05.22 |
|---|---|
| Chapter6. Model-Free Control (0) | 2023.05.22 |
| Chapter4. Model-based Planning (0) | 2023.05.21 |
| Chapter3. Markov Decision Process (0) | 2023.05.21 |
| Chapter 2 Reinforcement Learning Overview (0) | 2023.05.21 |



