지난 Chapter 내용을 간단히 복습해보겠습니다.
우리가 실제 모델을 알지 못할 때는 어떻게 해야 하는지, 일반화된 정책 개선 방법에 대해 배웠습니다. 탐험의 중요성을 이해하고, MC와 TD를 사용한 모델 없는 제어에 대해서도 알아보았습니다. SARSA와 Q-러닝에 대해서도 다루었습니다.
실제 모델을 알지 못할 때에도 모델 없는 강화 학습을 사용하여 최적의 정책을 학습하는 방법을 알아보았습니다. MC와 TD를 사용하여 정책을 개선하는 방법에 대해서도 살펴보았습니다. 또한, SARSA와 Q-러닝 알고리즘을 이용하여 최적의 행동 가치 함수를 학습하는 방법에 대해서도 다루었습니다.

Example : Q-Table for FrozenLake
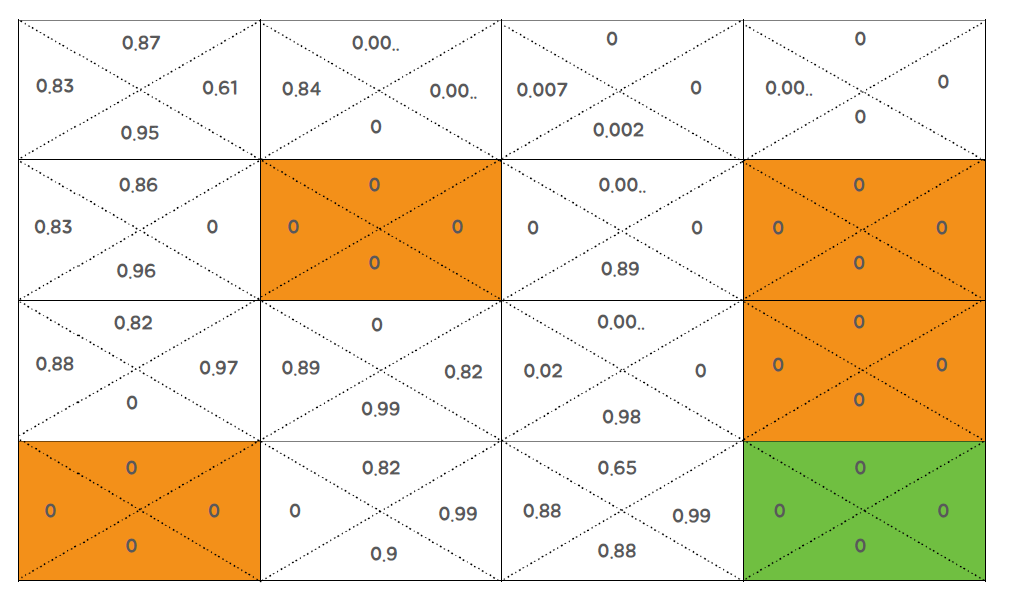
Limitation of Q-Learning using a Q-Table
Q 테이블을 사용한 강화 학습의 한계점을 예시로서 FrozenLake 문제를 통해 설명해보겠습니다. FrozenLake은 작은 크기의 맵(4 x 4)을 가지고 있으며, 각 상태에서 가능한 행동의 수는 4개입니다. 따라서 Q 테이블은 64개의 상태 (4 x 4 위치 x 4 행동)를 표현해야 합니다.
하지만 만약 크기가 더 큰 문제라면 어떨까요? 큰 문제의 경우 상태 공간의 크기가 기하급수적으로 증가하여 Q 테이블을 효율적으로 사용하는 것이 어려워집니다. 예를 들어, 맵의 크기가 10 x 10이라면 상태의 수는 100개이고 각 상태에서 가능한 행동의 수가 여전히 4개라면 Q 테이블의 크기는 400개가 됩니다. 상태 공간이 커질수록 Q 테이블의 크기도 기하급수적으로 증가하게 되는데, 이는 메모리 요구량과 계산 복잡도를 크게 증가시키는 문제를 야기할 수 있습니다.
따라서 큰 문제에서 Q 테이블을 사용하는 것은 실용적이지 않을 수 있습니다. 이러한 경우에는 상태 공간의 차원을 줄이거나 함수 근사를 사용하는 등의 방법을 통해 문제를 해결하는 것이 필요합니다. 함수 근사를 사용하면 상태-행동 값 함수를 파라미터화하여 근사적으로 표현하고, 이를 업데이트하는 방식으로 학습을 진행할 수 있습니다.
큰 문제에서 Q 테이블의 한계를 극복하기 위해 다양한 방법과 알고리즘이 개발되었으며, 이를 통해 더 복잡하고 대규모의 문제에 대한 강화 학습을 수행할 수 있게 되었습니다.
Large-scale Problem Examples

Model free RL을 어떻게 확장할 수 있을까요?
Value Function Approximation
지금까지는 값 함수를 룩업 테이블로 표현했습니다. 각 상태 s에는 V(s)라는 항목이 있었고, 각 상태-행동 쌍 s, a에는 Q(s, a)라는 항목이 있었습니다. 하지만 대규모 MDP(Markov Decision Process)의 경우에는 문제가 발생합니다. 상태나 행동이 너무 많아서 모두 메모리에 저장하기 어렵거나, 각 상태의 값을 개별적으로 학습하는 데 시간이 너무 오래 걸리는 경우가 있습니다. 이러한 대규모 MDP의 문제를 해결하기 위해 함수 근사를 사용하여 값 함수를 추정하는 방법이 있습니다. 이 때, 파라미터화된 함수를 사용하여 값을 근사적으로 표현합니다.

함수 근사를 통해 값 함수를 추정하면 상태나 행동의 수에 관계없이 일부 파라미터만을 이용하여 값을 계산할 수 있습니다.
이를 통해 대규모 MDP에 대한 강화 학습을 수행할 수 있으며, 메모리 요구량과 학습 시간을 크게 줄일 수 있습니다.
함수 근사에는 다양한 기법과 알고리즘이 사용되며, 주로 신경망, 선형 모델, 트리 기반 모델 등이 사용됩니다.
함수 근사를 사용하면 값 함수 추정이 더 효율적이고 실용적으로 가능해지며, 이를 통해 대규모이고 복잡한 문제에 대한 강화 학습을 수행할 수 있습니다.
Type of Value Function Approximation
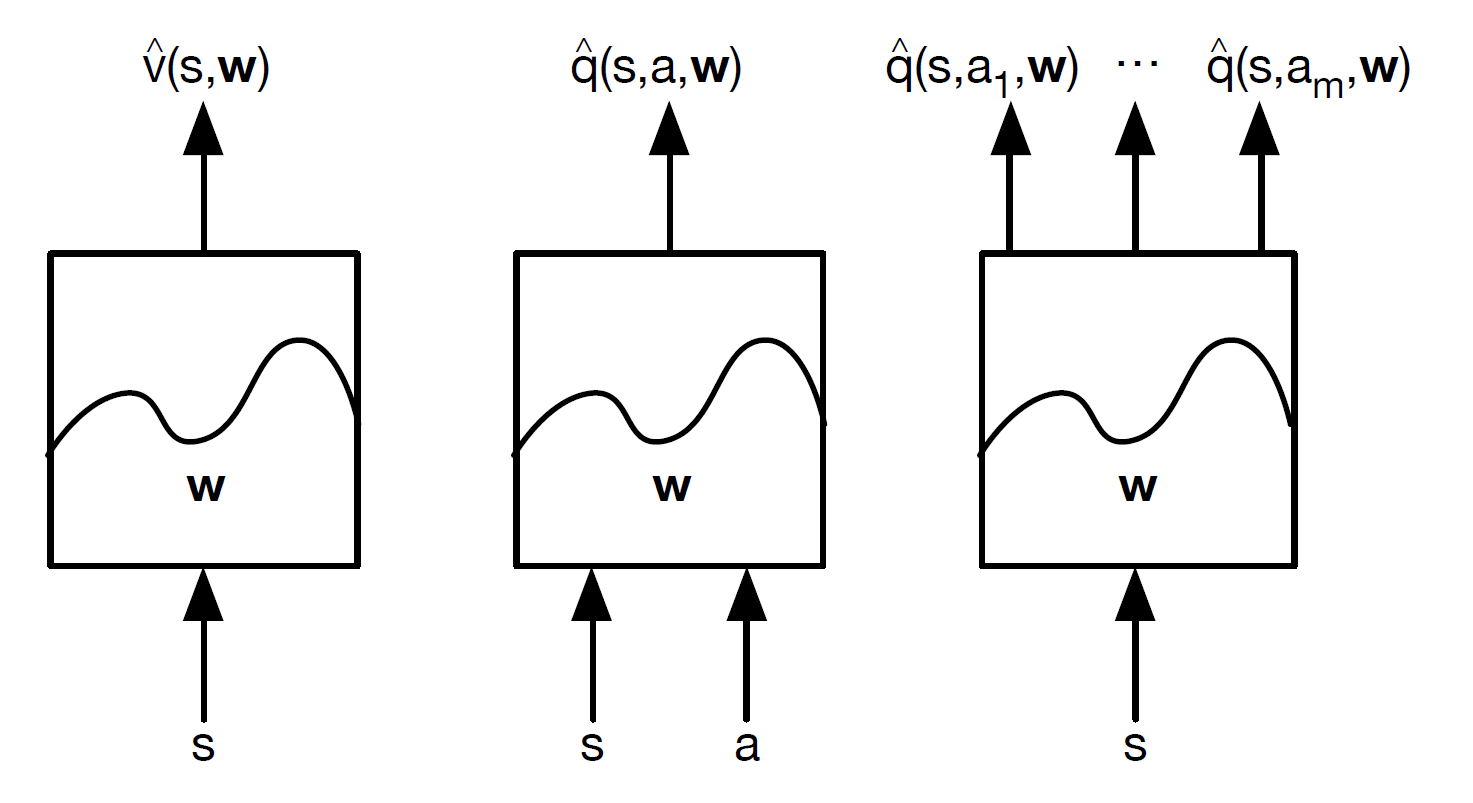
Motivation for VFA
• 각각의 개별 상태에 대해 명시적으로 저장하거나 학습할 필요가 없습니다.
• 동적 모델이나 보상 모델을 대신 사용합니다.
• 값 함수, 상태-행동 값 함수, 정책 등을 보다 간결한 표현으로 나타낼 수 있습니다.
• 상태들 사이에서 일반화할 수 있는 더 압축된 표현을 원합니다.
Benefits of Generalization
• (𝑃,𝑅)/𝑉/𝑄/𝜋을 저장하는 데 필요한 메모리를 줄일 수 있습니다.
• (𝑃,𝑅)/𝑉/𝑄/𝜋을 계산하는 데 필요한 계산량을 줄일 수 있습니다.
• 좋은 (𝑃,𝑅)/𝑉/𝑄/𝜋을 찾기 위해 필요한 경험을 줄일 수 있습니다.
Function Approximators
함수 근사에는 다양한 방법이 있습니다:
• 특성들의 선형 조합
• 신경망
• 결정 트리
• 최근접 이웃
• 푸리에/웨이블릿 기저 등
이 강의에서는 미분 가능한 함수 근사 방법에 초점을 맞출 것입니다:
• 선형 특성 표현
• 신경망
Review: Gradient Descent (https://junhan-ai.tistory.com/2)
Value Function Approx. By Stochastic Gradient Descent
확률적 경사 하강법을 사용하여 값 함수를 근사화합니다.
• 목표: 근사 값 함수 ො 𝑣(𝑠,𝑤)와 실제 값 함수 𝑣(𝑠) 사이의 평균 제곱 오차를 최소화하는 매개 변수 벡터 𝑤를 찾는 것입니다.
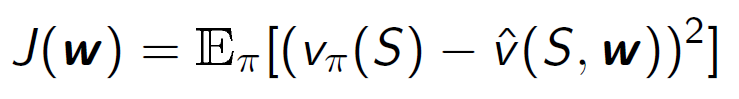
• 경사 하강법은 지역 최솟값을 찾습니다.
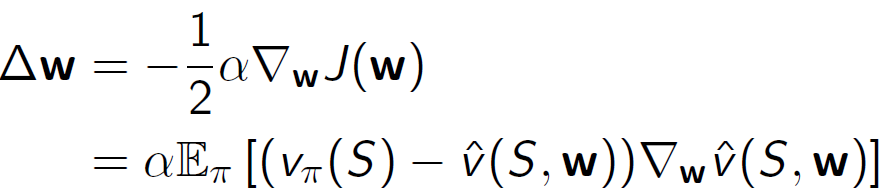
• 확률적 경사 하강법은 그레이디언트를 샘플링합니다.
이 방법을 사용하면 값 함수 근사화에 필요한 파라미터 벡터를 효과적으로 학습할 수 있습니다.
Feature Vectors
• 상태를 특징 벡터로 표현합니다.
• 예를 들어:
- 로봇과 랜드마크 사이의 거리
- 주식 시장의 추세
- 체스에서의 말의 배치

특징 벡터는 상태를 표현하기 위해 사용되는 값의 모음입니다. 각 특징은 해당 상태에서 중요한 정보를 나타내며, 학습 알고리즘이 이러한 특징을 기반으로 값을 근사화하고 예측하는 데 사용합니다. 이를 통해 복잡한 문제를 효과적으로 처리할 수 있습니다.
Linear Value Function Approximation
• 가치 함수를 특징들의 선형 조합으로 표현합니다.
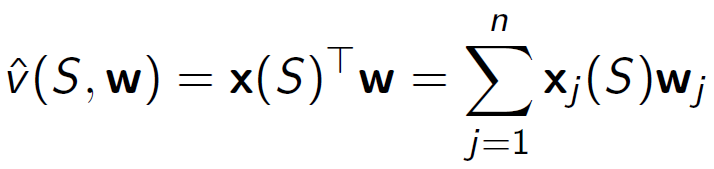
• 목적 함수는 파라미터 𝑤에 대해 이차식입니다.
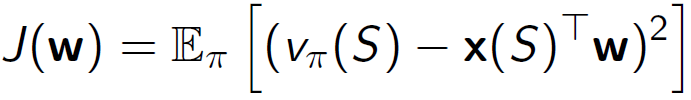
• 업데이트는 다음과 같습니다.

선형 가치 함수 근사화는 가치 함수를 선형 모델로 근사화하는 방법입니다. 각 특징은 가중치와 함께 곱해져 가치 함수를 계산하고 예측합니다. 목적 함수는 파라미터 𝑤를 최적화하는데 사용되며, 이를 통해 가치 함수를 효과적으로 학습할 수 있습니다. 업데이트 단계에서는 경사 하강법을 사용하여 파라미터를 조정하고 예측 오차를 최소화합니다.
Incremental Prediction Algorithms
• 지금까지는 감독자에 의해 제공되는 실제 가치 함수 𝑣𝜋(𝑠)가 있다고 가정했습니다.
• 하지만 강화학습에서는 감독자가 없고 보상만 존재합니다.
• 실제로는 𝑣𝜋(𝑠)에 대한 대체 타겟을 사용합니다.
• MC의 경우, 타겟은 반환값 𝐺𝑡입니다.

• TD의 경우, 타겟은 TD 타겟인 𝑅𝑡+1+𝛾𝑣𝑆𝑡+1,𝑤입니다.

증분적 예측 알고리즘은 감독자가 없는 상황에서 가치 함수를 추정하기 위해 사용됩니다. 강화학습에서는 타겟 값을 사용하여 추정된 가치 함수를 업데이트합니다. MC의 경우, 반환값이 예측의 타겟으로 사용되며, TD의 경우 TD 타겟이 타겟으로 사용됩니다. 이러한 타겟 값을 활용하여 예측 오차를 줄이고 가치 함수를 점진적으로 업데이트합니다.
Control with Value Function Approximation

• 정책 평가 (Approximate Policy Evaluation): 𝑞(𝑠,𝑎,𝑤)≈𝑞𝜋
• 정책 개선 (𝜖-Greedy Policy Improvement)
가치 함수 근사를 사용한 제어에서는 주어진 정책에 대한 가치 함수를 근사적으로 평가합니다. 이를 위해 가치 함수를 근사하는 함수 근사기를 사용하여 𝑞(𝑠,𝑎,𝑤)를 추정합니다. 이렇게 추정된 가치 함수를 기반으로 𝜖-Greedy 정책 개선을 수행하여 정책을 개선합니다.
가치 함수 근사를 사용한 제어는 주어진 정책에 대한 가치 함수를 근사하여 제어 문제를 해결하는 방법입니다.
Action Value Function Approximation
• 행동 가치 함수를 근사합니다.
𝑞(𝑆,𝐴,𝑤)≈𝑞𝜋
• 근사 행동 가치 𝑞(𝑆,𝐴,𝑤)와 실제 행동 가치 𝑞𝜋(𝑆,𝐴) 사이의 평균 제곱 오차를 최소화합니다.
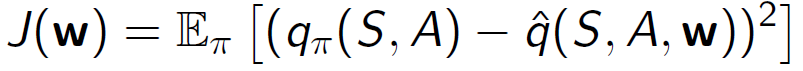
• 확률적 경사 하강법을 사용합니다.

행동 가치 함수 근사는 주어진 상태와 행동에 대한 행동 가치 함수를 근사하는 방법입니다. 이를 위해 행동 가치 함수를 근사하는 함수 근사기를 사용하여 𝑞(𝑆,𝐴,𝑤)를 추정합니다. 추정된 근사 행동 가치와 실제 행동 가치 사이의 평균 제곱 오차를 최소화하는 방식으로 학습을 진행합니다. 이를 위해 확률적 경사 하강법을 사용하여 근사 행동 가치 함수의 파라미터를 업데이트합니다.
Linear Action Value Function Approximation
• 상태와 행동을 특성 벡터로 나타냅니다.

• 행동 가치 함수를 특성의 선형 조합으로 나타냅니다.
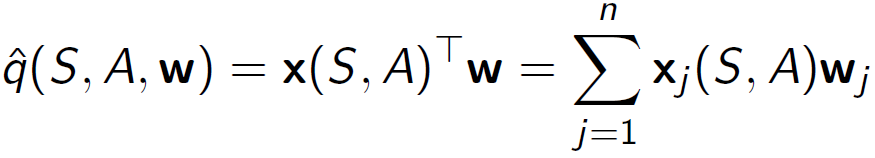
선형 행동 가치 함수 근사는 상태와 행동을 특성 벡터로 표현하고, 행동 가치 함수를 특성의 선형 조합으로 근사하는 방법입니다. 특성 벡터는 상태와 행동에 대한 특징을 나타내는 값들로 구성됩니다. 선형 조합은 특성 벡터의 각 요소와 그에 대응하는 가중치의 곱을 합하여 행동 가치 함수의 근사값을 계산합니다. 이를 통해 주어진 상태와 행동에 대한 행동 가치를 근사하는 것이 목표입니다.
Incremental Control Algorithms
예측과 마찬가지로 𝑄𝜋(𝑆,𝐴)에 대한 대체 타겟을 사용해야 합니다.
• MC (Monte Carlo)의 경우, 타겟은 반환값 𝐺𝑡입니다.
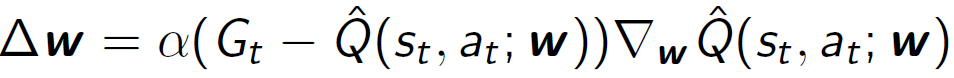
• SARSA의 경우, 현재 함수 근사값을 활용한 TD 타겟인 𝑅+𝛾𝑄(𝑠′,𝑎′,𝑤)를 사용합니다.
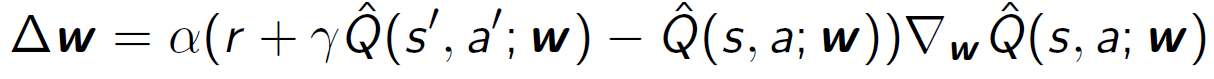
• Q-learning의 경우, 현재 함수 근사값을 활용한 TD 타겟인 𝑅+𝛾max𝑎𝑄(𝑠′,𝑎′,𝑤)를 사용합니다.

증분형 제어 알고리즘에서는 𝑄(𝑠,𝑎)의 근사값을 업데이트하기 위해 위의 타겟을 사용합니다. 이를 통해 현재의 함수 근사값을 활용하여 행동 가치를 업데이트하며, 최적의 정책을 찾는 것이 목표입니다.
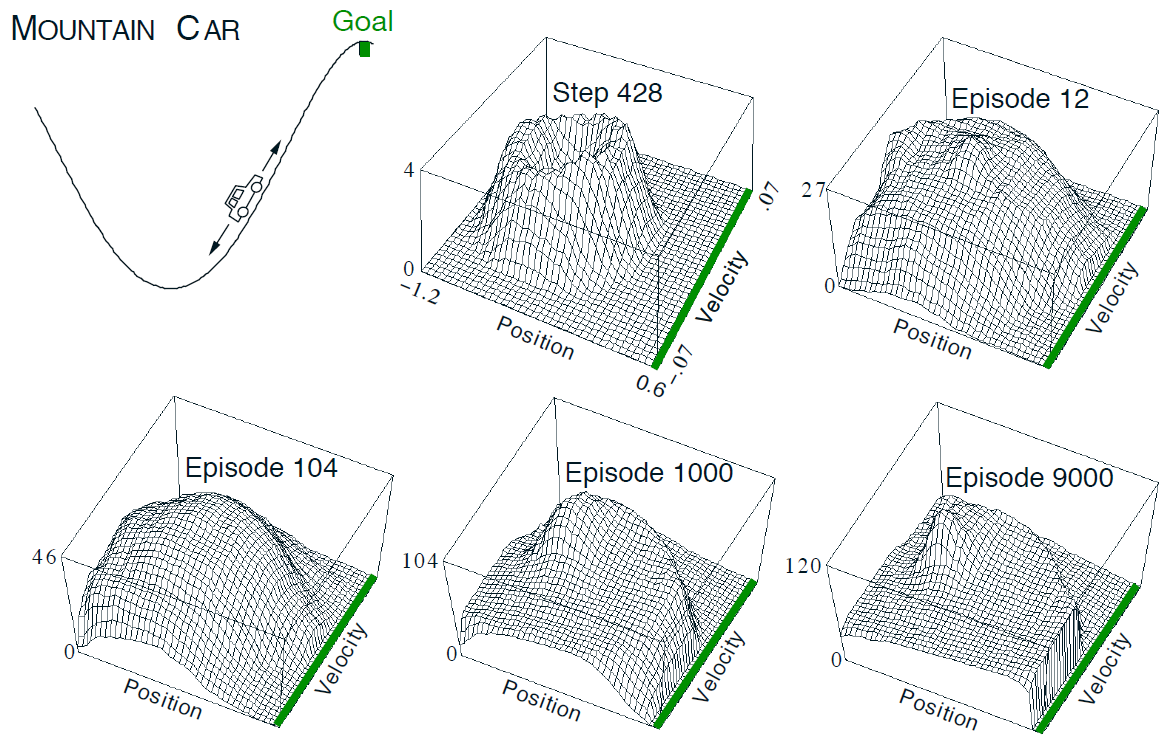
Deep Reinforcement Learning
심층 신경망을 사용하여 다음과 같은 요소들을 표현합니다.
• 가치 함수 (Value function)
• 정책 (Policy)
• 모델 (Model)
이들을 신경망의 구조를 통해 표현하고, 확률적 경사 하강법 (Stochastic Gradient Descent, SGD)을 사용하여 손실 함수를 최적화합니다.
심층 강화학습은 기존의 강화학습 방법과 달리 신경망을 활용하여 높은 차원의 입력과 복잡한 환경을 다룰 수 있습니다. 이를 통해 더 복잡한 문제에 대한 학습과 일반화를 달성할 수 있습니다.
Deep Q-Networks (DQNs)
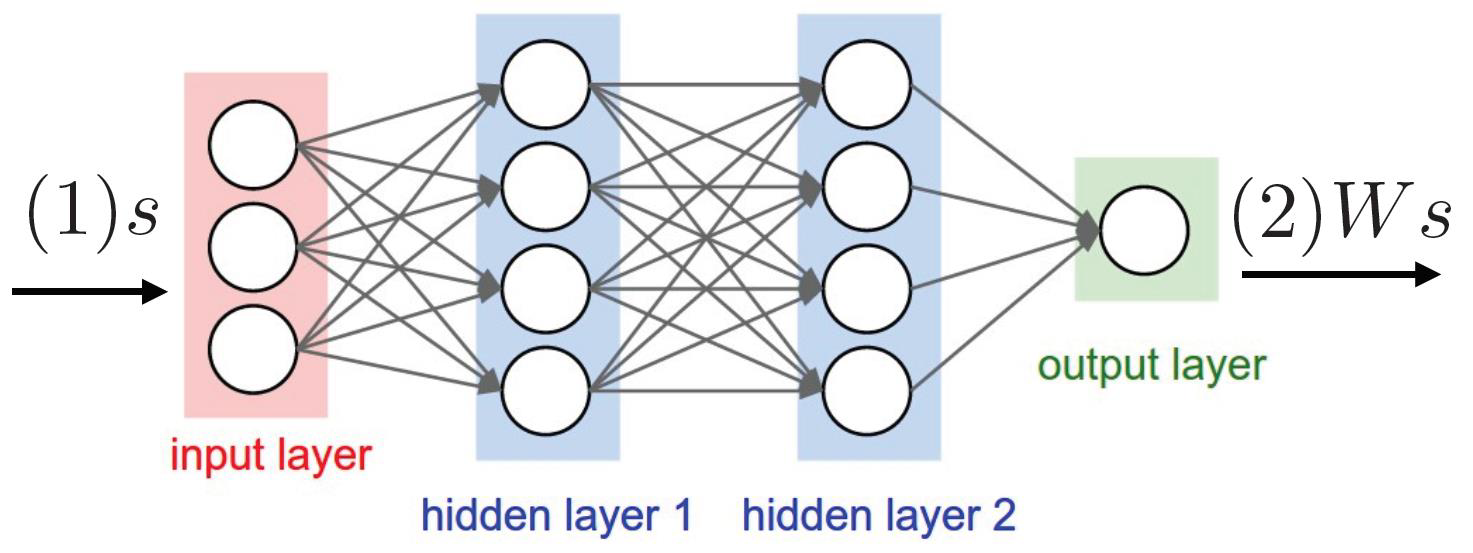
딥 Q-네트워크는 상태-행동 가치 함수를 가중치 𝑤로 표현하는 모델입니다. 이 모델은 심층 신경망을 기반으로 구성되며, 각 상태와 행동의 조합에 대한 가치를 추정하는 역할을 수행합니다.
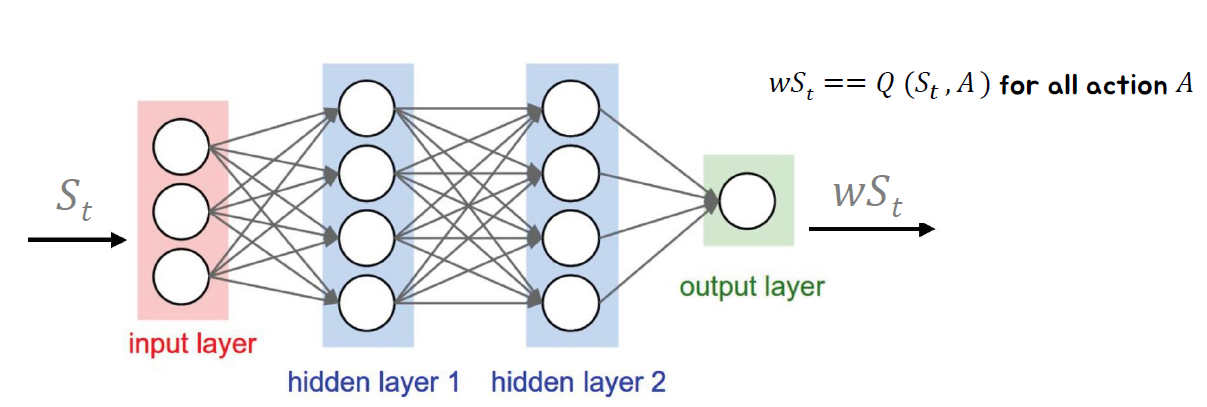
DQN은 딥 강화학습에서 중요한 알고리즘으로, 이 네트워크는 대규모 상태-행동 공간을 처리하고, 복잡한 환경에서도 학습과 일반화를 효과적으로 수행할 수 있습니다. DQN은 Q-러닝 알고리즘을 기반으로 하며, 경험 재생 (experience replay)과 타겟 네트워크 (target network)를 사용하여 학습의 안정성과 성능을 향상시킵니다.
Deep Q-Network Training
딥 Q-네트워크의 학습은 다음과 같은 절차를 따릅니다:

- 초기화: 네트워크의 가중치를 무작위로 초기화합니다.
- 상태 관찰: 환경에서 현재 상태를 관찰합니다.
- 행동 선택: 𝑞값을 기반으로 탐욕적인 정책을 사용하여 행동을 선택합니다. 일정한 확률(탐색 비율)로 무작위 행동을 선택할 수도 있습니다.
- 행동 실행: 선택한 행동을 환경에 적용하고, 다음 상태와 보상을 관찰합니다.
- 경험 저장: 상태, 행동, 보상, 다음 상태를 경험 버퍼에 저장합니다.
- 경험 샘플링: 경험 버퍼에서 무작위로 일부 경험을 선택하여 학습에 사용합니다.
- 타겟 계산: 선택한 경험을 기반으로 타겟 Q-값을 계산합니다. 이는 타겟 네트워크를 사용하여 계산할 수도 있습니다.
- 손실 계산: 타겟 Q-값과 현재 Q-값의 차이를 최소화하는 손실 함수를 계산합니다.
- 역전파: 손실 함수를 사용하여 역전파를 수행하여 네트워크의 가중치를 업데이트합니다.
- 반복: 위 단계를 반복하여 네트워크를 계속해서 학습시킵니다.
딥 Q-네트워크의 학습은 경험의 다양성을 활용하고, 타겟 네트워크를 사용하여 학습의 안정성을 높이는 등의 기법을 적용할 수 있습니다. 이를 통해 딥 Q-네트워크는 복잡한 환경에서도 뛰어난 성능을 발휘할 수 있습니다.
Example:CartPole in OpenAI Gym
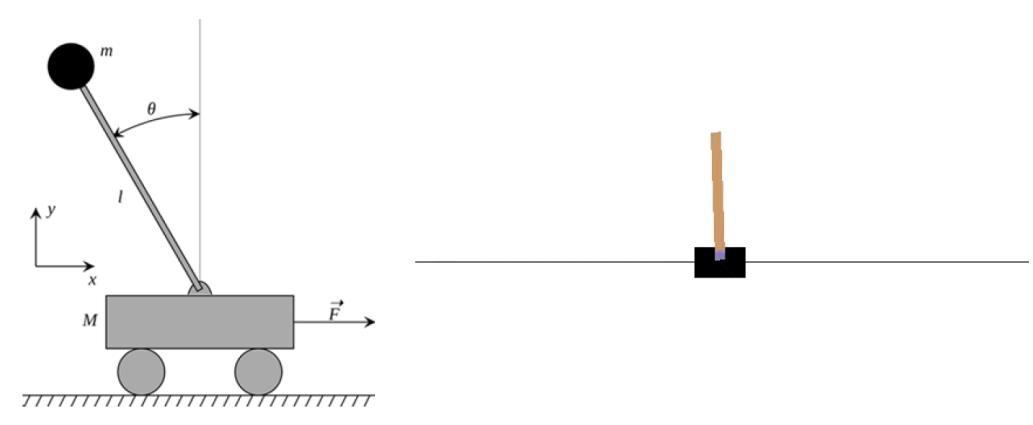
• 목표: 움직이는 카트 위에 막대를 균형잡기
• 상태: 막대의 각도, 각속도, 카트의 위치, 수평 속도
• 행동: 카트에 가해지는 수평 힘 (예: 왼쪽으로 가속, 오른쪽으로 가속)
• 보상: 막대가 수직 상태를 유지할 때마다 각 시간 단계마다 보상 1점
Convergence Issues
• 𝑞(𝑆𝑡,𝐴𝑡,𝑤)는 학습자의 현재 근사값으로 𝑞(𝑆𝑡,𝐴𝑡)를 나타냅니다.
• 최소화

• 테이블 룩업 표현을 사용할 때는 𝑞∗로 수렴하지만, 신경망을 사용할 때는 다음과 같은 이유로 발산할 수 있습니다:
- 샘플 간 상관관계
- 비정상적인 타깃
딥 Q-네트워크(DQN) 학습 시에는 이러한 수렴 문제가 발생할 수 있습니다. 신경망은 샘플 간 상관관계와 타깃의 비정상성 때문에 수렴하지 않을 수 있습니다. 이러한 문제를 해결하기 위해 몇 가지 기법을 적용할 수 있습니다. 예를 들어, 타깃 네트워크를 사용하여 타깃 값을 안정화하고, 경험 재생 메모리를 사용하여 상관관계를 줄일 수 있습니다. 또한, 학습률 스케줄링, 정규화, 더 작은 학습 단계 등의 기법을 적용하여 네트워크의 안정성을 향상시킬 수 있습니다.
딥 Q-네트워크 학습에서 수렴 문제를 다루는 것은 중요한 과제이며, 다양한 기법을 시도하고 조정하여 최적의 결과를 얻을 수 있도록 해야 합니다.
Correlations between samples(샘플 간 상관관계)

Non stationary targets
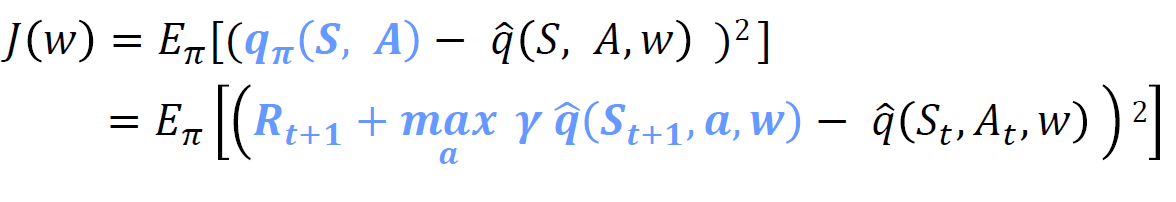
• 우리는 추정치를 추정치로 업데이트합니다.
• 예측 𝑄를 업데이트할 때마다 타깃 𝑄도 영향을 받습니다.
• 타깃 𝑄를 예측 𝑄와 분리해야 합니다.
딥 Q-네트워크 학습에서 발생하는 비정상적인 타깃 문제는 업데이트하는 동안 타깃 값이 예측 값을 변경하기 때문에 발생합니다. 이로 인해 네트워크가 수렴하지 않을 수 있습니다. 이 문제를 해결하기 위해 "타깃 네트워크"라고 알려진 별도의 네트워크를 사용하여 예측과 타깃을 분리할 수 있습니다. 타깃 네트워크는 일정한 간격으로 예측 네트워크의 가중치를 복사하여 사용하며, 이를 통해 안정적인 타깃 값을 유지할 수 있습니다. 이를 통해 비정상적인 타깃 문제를 완화하고 학습의 안정성을 향상시킬 수 있습니다.
Deep Q-Networks (DQN) [NIPS 2013], [Nature2015]
• 심층 신경망
• 경험 재생 (Experience Replay)
- 샘플들 간의 상관관계 해결
• 고정된 타깃 (Fixed Target)
- 비정상적인 타깃 문제 해결
딥 Q-네트워크 (DQN)은 강화학습에서 널리 사용되는 알고리즘입니다. DQN은 딥 신경망을 사용하여 Q-값을 근사화하며, 이를 통해 복잡한 환경에서도 고차원 상태 공간을 다룰 수 있습니다.
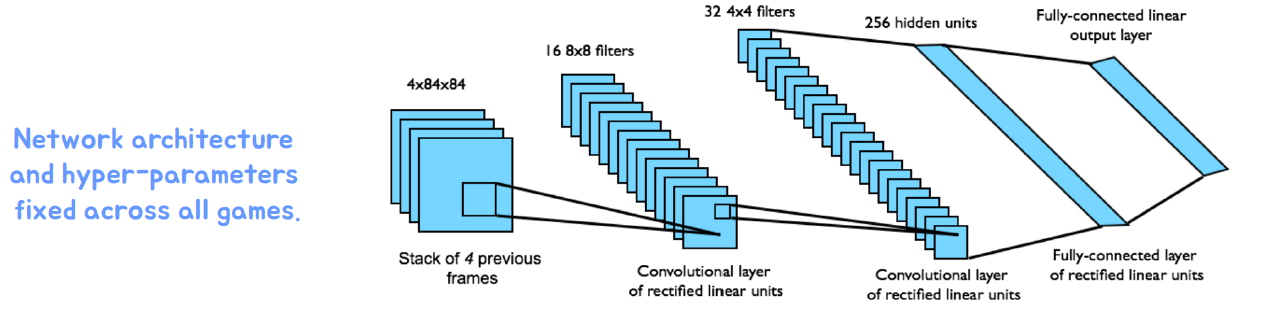
DQN의 핵심 개념 중 하나는 "경험 재생"입니다. 경험 재생은 에이전트가 이전에 경험한 상태 및 행동 샘플을 저장하고, 이를 임의로 선택하여 네트워크를 학습시키는 것입니다. 이를 통해 샘플들 간의 상관관계를 해결하고 학습의 안정성을 향상시킬 수 있습니다. 예) 경험 (𝑠𝑡,𝑎𝑡,𝑟𝑡+1,𝑠𝑡+1)를 리플레이 메모리𝐷에 저장


또한, DQN은 "고정된 타깃"을 사용하여 비정상적인 타깃 문제를 해결합니다. 타깃 네트워크를 사용하여 예측 네트워크의 가중치를 일정한 간격으로 복사하여 타깃 값을 유지합니다. 이를 통해 타깃 값의 비정상적인 변화를 완화하고 학습의 안정성을 개선할 수 있습니다.
딥 Q-네트워크 (DQN)는 강화학습 분야에서의 중요한 알고리즘으로서 다양한 문제에 적용될 수 있으며, 이를 통해 높은 성능과 안정성을 달성할 수 있습니다.
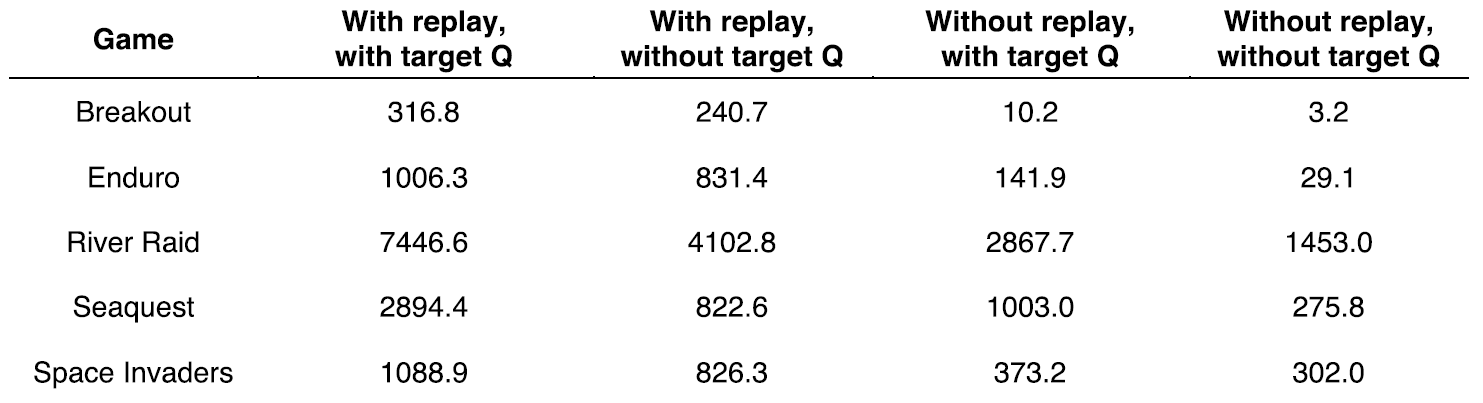
DQN Results on 49 Atari Games

The effects of experience replay and fixed target network
DQNs Summary
• DQN은 경험 재생과 고정된 Q 타깃을 사용합니다.
• 전이 (𝑠𝑡,𝑎𝑡,𝑟𝑡+1,𝑠𝑡+1)를 재생 메모리 𝐷에 저장합니다.
• 𝐷에서 무작위 미니 배치의 전이 (𝑠,𝑎,𝑟,𝑠′)를 샘플링합니다.
• 이전에 고정된 매개변수 𝑤−에 대한 Q 학습 타깃을 계산합니다.
• Q 네트워크와 Q 학습 타깃 사이의 평균 제곱 오차(MSE)를 최소화합니다.
• 확률적 경사 하강법을 사용합니다.
'강화학습' 카테고리의 다른 글
| Chapter 9. Policy Gradients (0) | 2023.05.22 |
|---|---|
| Chapter 8. Advanced Value Function Approximation (0) | 2023.05.22 |
| Chapter6. Model-Free Control (0) | 2023.05.22 |
| Chapter 5. Model-free Prediction (1) | 2023.05.21 |
| Chapter4. Model-based Planning (0) | 2023.05.21 |



