https://proceedings.neurips.cc/paper/2012/hash/c399862d3b9d6b76c8436e924a68c45b-Abstract.html
ImageNet Classification with Deep Convolutional Neural Networks
Requests for name changes in the electronic proceedings will be accepted with no questions asked. However name changes may cause bibliographic tracking issues. Authors are asked to consider this carefully and discuss it with their co-authors prior to reque
proceedings.neurips.cc
초록
우리는 ImageNet LSVRC-2010 대회의 1.2백만 개의 고해상도 이미지를 1000개의 서로 다른 클래스들로 분류하기 위해 대규모, 깊은 합성곱 신경망(convolutional neural network, CNN)을 훈련시켰습니다. 테스트 데이터에서 우리는 top-1 에러율 37.5%와 top-5 에러율 17.0%를 달성했으며, 이는 이전의 최첨단 성능보다 상당히 뛰어났습니다. 이 신경망은 6천만 개의 파라미터와 65만 개의 뉴런을 포함하고 있으며, 5개의 합성곱 계층으로 구성되어 있습니다. 이 중 일부 계층 뒤에는 최대 풀링(max-pooling) 계층이 있으며, 마지막으로 1000개의 출력을 갖는 소프트맥스(softmax) 계층이 있는 3개의 완전 연결(fully-connected) 계층이 있습니다. 훈련 속도를 높이기 위해 우리는 비포화(non-saturating) 뉴런을 사용했으며, 합성곱 연산의 매우 효율적인 GPU 구현을 적용했습니다. 완전 연결 계층에서 과적합을 줄이기 위해 "드롭아웃(dropout)"이라는 최근 개발된 정규화 기법을 사용했으며, 이는 매우 효과적임을 입증했습니다. 우리는 또한 이 모델의 변형을 ILSVRC-2012 대회에 제출하여 top-5 테스트 에러율 15.3%를 달성했으며, 이는 26.2%를 기록한 2등 엔트리보다 우수한 성과였습니다.
1 서론
현재의 객체 인식 방법들은 본질적으로 기계 학습 기법을 사용하고 있습니다. 성능을 향상시키기 위해 우리는 더 큰 데이터셋을 수집하고, 더 강력한 모델을 학습하며, 과적합을 방지하기 위한 더 나은 기법들을 사용할 수 있습니다. 최근까지도, 라벨이 달린 이미지 데이터셋은 비교적 작았으며, 수만 장의 이미지 수준이었습니다(예: NORB [16], Caltech-101/256 [8, 9], CIFAR-10/100 [12]). 이러한 규모의 데이터셋으로 간단한 인식 작업은 특히 라벨을 보존하는 변환으로 증강된 경우 상당히 잘 해결할 수 있습니다. 예를 들어, MNIST 숫자 인식 작업에서 현재 최고 오류율은 0.3% 미만으로 인간 성능에 근접하고 있습니다 [4]. 그러나 현실적인 환경에서의 객체들은 상당한 변화를 보이기 때문에, 그들을 인식하기 위해서는 더 큰 훈련 세트가 필요합니다. 실제로 작은 이미지 데이터셋의 한계는 널리 인식되고 있었지만 (예: Pinto et al. [21]), 수백만 장의 라벨이 달린 데이터를 수집하는 것이 최근에야 가능해졌습니다. 새로운 더 큰 데이터셋에는 수십만 개의 완전히 분할된 이미지를 포함하는 LabelMe [23]와, 15백만 장 이상의 라벨이 달린 고해상도 이미지를 22,000개 이상의 카테고리로 나눈 ImageNet [6]이 포함됩니다.
수백만 개의 이미지로부터 수천 개의 객체를 학습하려면, 학습 용량이 큰 모델이 필요합니다. 그러나 객체 인식 작업의 엄청난 복잡성으로 인해, ImageNet과 같은 대규모 데이터셋으로도 이 문제를 완전히 정의할 수 없으므로, 모델은 우리가 가지고 있지 않은 데이터에 대한 보상을 제공할 수 있는 많은 사전 지식도 포함해야 합니다. 합성곱 신경망(CNN)은 이러한 모델 중 하나입니다 [16, 11, 13, 18, 15, 22, 26]. CNN의 용량은 깊이와 넓이를 조절함으로써 제어할 수 있으며, 이미지의 특성(즉, 통계의 정지성 및 픽셀 의존성의 국소성)에 대해 강력하고 대체로 정확한 가정을 합니다. 따라서 비슷한 크기의 계층을 가진 표준 피드포워드 신경망에 비해 CNN은 연결과 파라미터가 훨씬 적어 훈련이 더 용이하며, 이론적으로 최상의 성능은 약간 더 나쁠 수 있지만 큰 차이는 아닙니다.
CNN의 매력적인 특성과 지역 아키텍처의 상대적 효율성에도 불구하고, 여전히 대규모로 고해상도 이미지에 적용하는 것은 금전적 부담이 컸습니다. 다행히도, 현재의 GPU는 2D 합성곱의 고도로 최적화된 구현과 결합하여 흥미롭게도 큰 CNN을 훈련할 수 있을 만큼 강력해졌으며, 최근의 ImageNet과 같은 데이터셋은 심각한 과적합 없이 이러한 모델을 훈련할 수 있을 만큼 충분한 라벨이 달린 예제를 포함하고 있습니다.
이 논문의 구체적인 기여는 다음과 같습니다: 우리는 ImageNet의 ILSVRC-2010과 ILSVRC-2012 대회에서 사용된 하위 데이터셋에 대해 지금까지 가장 큰 합성곱 신경망 중 하나를 훈련시켰으며, 이 데이터셋에서 사상 최고 성과를 달성했습니다. 우리는 2D 합성곱 및 합성곱 신경망 훈련에 본질적인 모든 다른 연산을 고도로 최적화된 GPU 구현으로 작성했으며, 이를 공개적으로 제공했습니다. 우리의 네트워크는 성능을 개선하고 훈련 시간을 줄이는 여러 가지 새로운 기능들을 포함하고 있으며, 이는 3장에서 자세히 설명합니다. 120만 개의 라벨이 달린 훈련 예제를 사용해도 네트워크의 크기로 인해 과적합이 중요한 문제로 대두되었기 때문에, 우리는 이를 방지하기 위한 여러 가지 효과적인 기법을 사용했으며, 이는 4장에서 설명합니다. 최종 네트워크는 5개의 합성곱 계층과 3개의 완전 연결 계층으로 구성되었으며, 이 깊이는 매우 중요한 것으로 보입니다. 합성곱 계층 중 하나라도 제거하면 성능이 저하되었으며, 각 계층은 모델의 파라미터 중 1% 미만을 포함합니다.
결국, 네트워크의 크기는 주로 현재 GPU의 메모리 용량과 우리가 수용할 수 있는 훈련 시간에 의해 제한됩니다. 우리의 네트워크는 두 개의 GTX 580 3GB GPU에서 5일에서 6일 동안 훈련됩니다. 우리의 모든 실험은 더 빠른 GPU와 더 큰 데이터셋이 제공되면 우리의 결과가 단순히 개선될 수 있음을 시사합니다.
2 데이터셋
ImageNet은 약 22,000개의 카테고리에 속하는 1,500만 장 이상의 라벨이 달린 고해상도 이미지로 구성된 데이터셋입니다. 이 이미지들은 웹에서 수집되었으며, Amazon의 Mechanical Turk 크라우드소싱 도구를 사용해 인간 라벨러들에 의해 라벨링되었습니다. 2010년부터 Pascal Visual Object Challenge의 일환으로 매년 ImageNet Large-Scale Visual Recognition Challenge(ILSVRC)라는 대회가 열리고 있습니다. ILSVRC는 ImageNet의 하위 집합을 사용하며, 1,000개의 카테고리마다 약 1,000장의 이미지가 포함됩니다. 총 120만 장의 훈련 이미지, 5만 장의 검증 이미지, 그리고 15만 장의 테스트 이미지가 있습니다.
ILSVRC-2010은 테스트 세트 라벨이 공개된 유일한 ILSVRC 버전으로, 우리는 주로 이 버전을 사용해 실험을 진행했습니다. 또한 우리는 ILSVRC-2012 대회에도 참가했기 때문에, 6장에서 해당 데이터셋 버전에서의 결과도 보고합니다. 이 버전에서는 테스트 세트 라벨이 공개되지 않았습니다. ImageNet에서는 두 가지 오류율을 보고하는 것이 관례입니다: top-1 오류율과 top-5 오류율입니다. top-5 오류율은 모델이 가장 가능성이 높다고 판단한 다섯 개의 라벨 안에 정답이 없는 테스트 이미지의 비율을 의미합니다.
ImageNet은 해상도가 다양한 이미지로 구성되어 있지만, 우리의 시스템은 일정한 입력 크기를 요구합니다. 따라서 우리는 이미지를 고정된 해상도인 256 x 256으로 다운샘플링했습니다. 직사각형 이미지의 경우, 먼저 짧은 쪽의 길이가 256이 되도록 이미지를 재조정한 다음, 결과 이미지에서 중앙 256 x 256 영역을 잘라냈습니다. 이외에는 특별한 전처리를 하지 않았으며, 각 픽셀에서 훈련 세트의 평균 활동값을 빼주는 것만 적용했습니다. 따라서 우리는 (중앙화된) 원시 RGB 픽셀 값을 사용해 네트워크를 훈련시켰습니다.
3 아키텍처
우리 네트워크의 아키텍처는 그림 2에 요약되어 있습니다. 이 네트워크는 학습 가능한 8개의 계층으로 구성되어 있으며, 그 중 5개는 합성곱 계층이고 3개는 완전 연결 계층입니다. 아래에서는 네트워크 아키텍처에서 새롭거나 특이한 몇 가지 특징을 설명합니다. 3.1-3.4절은 우리가 중요하다고 판단한 순서대로 정리되었으며, 가장 중요한 부분이 먼저 나옵니다.

그림 1: ReLU를 사용하는 4계층 합성곱 신경망(실선)은 tanh 뉴런을 사용하는 동등한 네트워크(점선)에 비해 CIFAR-10 데이터셋에서 25%의 훈련 오류율에 도달하는 속도가 6배 더 빠릅니다. 각 네트워크의 학습 속도를 최대로 하기 위해 학습률은 독립적으로 선택되었습니다. 이 실험에서는 어떠한 정규화도 적용되지 않았습니다. 여기서 나타난 효과의 크기는 네트워크 아키텍처에 따라 다르지만, ReLU를 사용하는 네트워크는 항상 포화 뉴런을 사용하는 네트워크보다 여러 배 빠르게 학습하는 경향이 있습니다.
3.1 ReLU 비선형성


3.2 다중 GPU에서의 훈련
하나의 GTX 580 GPU는 메모리가 3GB에 불과하여 훈련할 수 있는 네트워크의 최대 크기에 제약이 있습니다. 120만 개의 훈련 예제가 네트워크가 너무 커서 한 GPU에 모두 적재되지 않는 상황을 만들기에 충분하다는 것이 밝혀졌습니다. 따라서 우리는 네트워크를 두 개의 GPU에 분산시켰습니다. 현재의 GPU는 교차 GPU 병렬화에 특히 적합한데, 이는 GPU 간의 메모리를 직접 읽고 쓸 수 있어 호스트 머신 메모리를 거치지 않아도 되기 때문입니다. 우리가 사용한 병렬화 방식은 본질적으로 각 GPU에 절반의 커널(또는 뉴런)을 배치하는 것이지만, 하나의 추가적인 트릭이 있습니다: GPU들은 특정 계층에서만 서로 통신합니다. 예를 들어, 3번째 계층의 커널은 2번째 계층의 모든 커널 맵으로부터 입력을 받습니다. 하지만 4번째 계층의 커널은 같은 GPU에 있는 3번째 계층의 커널 맵으로부터만 입력을 받습니다. 이러한 연결 패턴을 선택하는 것은 교차 검증의 문제이지만, 이를 통해 계산량에 비해 통신량이 허용 가능한 비율로 조정되도록 정확하게 조정할 수 있습니다.
결과적으로 이 아키텍처는 Cireșan 등 [5]이 사용한 "열형(columnar)" CNN과 약간 유사하지만, 우리의 열은 독립적이지 않습니다(그림 2 참조). 이 방식은 각 합성곱 계층에서 절반의 커널만 사용하는 네트워크를 하나의 GPU에서 훈련했을 때와 비교하여, top-1 오류율을 1.7%, top-5 오류율을 1.2% 줄였습니다. 또한, 두 개의 GPU를 사용하는 네트워크는 하나의 GPU를 사용하는 네트워크보다 훈련 시간이 약간 더 짧습니다.
추가 설명: 하나의 GPU를 사용하는 네트워크는 실제로 두 GPU를 사용하는 네트워크와 마지막 합성곱 계층에서 동일한 수의 커널을 가지고 있습니다. 이는 네트워크의 대부분의 파라미터가 마지막 합성곱 계층을 입력으로 받는 첫 번째 완전 연결 계층에 있기 때문입니다. 따라서 두 네트워크가 대략 같은 수의 파라미터를 가지도록 하기 위해 마지막 합성곱 계층(및 그 뒤의 완전 연결 계층)의 크기를 절반으로 줄이지 않았습니다. 이로 인해 이 비교는 하나의 GPU를 사용하는 네트워크에 유리하게 작용하는데, 이는 두 GPU 네트워크의 "절반 크기"보다 크기 때문입니다.

그림 2: 우리의 CNN 아키텍처를 설명하는 그림으로, 두 GPU 간의 역할 분담을 명확하게 보여줍니다. 하나의 GPU는 그림 상단의 계층 부분을 실행하고, 다른 GPU는 하단의 계층 부분을 실행합니다. GPU들은 특정 계층에서만 서로 통신합니다. 네트워크의 입력은 150,528차원이고, 나머지 계층의 뉴런 수는 다음과 같습니다: 253,440–186,624–64,896–64,896–43,264–4096–4096–1000.
3.3 지역 응답 정규화

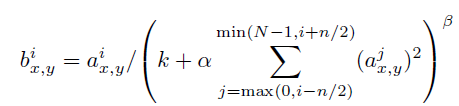
여기서 합(sum)은 동일한 공간 위치에서 "인접한" n개의 커널 맵에 대해 계산되며, N은 해당 계층의 총 커널 수를 나타냅니다. 커널 맵의 순서는 임의적으로 정해지며 훈련이 시작되기 전에 결정됩니다. 이러한 응답 정규화 방식은 실제 뉴런에서 발견되는 형태에서 영감을 받아 구현된 일종의 측면 억제를 수행하며, 서로 다른 커널을 사용해 계산된 뉴런 출력들 사이에서 큰 활성화를 두고 경쟁을 유도합니다. 여기서 사용된 상수들인 , , β, 그리고 는 하이퍼파라미터로, 검증 세트를 통해 그 값을 결정합니다. 우리는 k=2, n=5, β=10^{-4}, α=0.75의 값을 사용했습니다. 우리는 특정 계층에서 ReLU 비선형성을 적용한 후 이 정규화를 적용했습니다(3.5절 참조). 이 방식은 Jarrett 등 [11]의 지역 대비 정규화 방식과 유사하지만, 우리는 평균 활성도를 빼지 않기 때문에 더 정확히 말하면 "밝기 정규화"로 불립니다. 응답 정규화는 우리의 top-1 오류율을 1.4%, top-5 오류율을 1.2% 줄였습니다. 우리는 또한 이 방식을 CIFAR-10 데이터셋에서 확인했습니다: 4계층 CNN은 정규화를 적용하지 않았을 때 13%의 테스트 오류율을, 정규화를 적용했을 때 11%의 오류율을 기록했습니다.
(네트워크에 대한 상세 설명은 공간 제약으로 인해 포함하지 못했지만, 여기에서 제공되는 코드와 파라미터 파일로 정확히 명시되어 있습니다: http://code.google.com/p/cuda-convnet/.)
3.4 겹치는 풀링
CNN에서 풀링 계층은 동일한 커널 맵에서 이웃하는 뉴런 그룹의 출력을 요약합니다. 전통적으로 인접한 풀링 유닛이 요약하는 영역들은 겹치지 않습니다(예: [17, 11, 4]). 풀링 계층은 풀링 유닛들이 픽셀 간격으로 배치된 격자로 구성된 것으로 생각할 수 있으며, 각 유닛은 해당 위치를 중심으로 하는 z×z 크기의 영역을 요약합니다. s=z로 설정하면 전통적인 지역 풀링을 얻을 수 있으며, 이는 CNN에서 흔히 사용됩니다. 반면, s<z로 설정하면 겹치는 풀링이 됩니다. 우리는 네트워크 전반에서 이 겹치는 풀링 방식을 사용했으며, s=2, z=3을 적용했습니다. 이 방식은 s=2, z=2로 설정한 비겹치는 방식과 비교하여 top-1 오류율을 0.4%, top-5 오류율을 0.3% 줄였습니다. 훈련 중에는 일반적으로 겹치는 풀링을 사용한 모델이 과적합에 빠지기 약간 더 어려운 경향을 보였습니다.
3.5 전체 아키텍처
이제 우리 CNN의 전체 아키텍처를 설명할 준비가 되었습니다. 그림 2에 나타난 것처럼, 이 네트워크는 8개의 가중치가 있는 계층으로 구성됩니다. 첫 다섯 계층은 합성곱 계층이고, 나머지 세 계층은 완전 연결 계층입니다. 마지막 완전 연결 계층의 출력은 1000개의 클래스 레이블에 대한 분포를 생성하는 1000-방향 소프트맥스(softmax)로 전달됩니다. 우리의 네트워크는 다항 로지스틱 회귀 목표를 최대화하며, 이는 예측 분포에서 올바른 레이블의 로그 확률을 훈련 케이스마다 평균하여 최대화하는 것과 동일합니다.
두 번째, 네 번째, 다섯 번째 합성곱 계층의 커널은 이전 계층의 동일한 GPU에 있는 커널 맵에만 연결됩니다(그림 2 참조). 반면에, 세 번째 합성곱 계층의 커널은 두 번째 계층의 모든 커널 맵에 연결됩니다. 완전 연결 계층의 뉴런들은 이전 계층의 모든 뉴런들과 연결됩니다. 첫 번째와 두 번째 합성곱 계층 뒤에는 응답 정규화 계층이 있습니다. 최대 풀링 계층은 3.4절에서 설명된 것처럼 응답 정규화 계층 뒤와 다섯 번째 합성곱 계층 뒤에 위치합니다. ReLU 비선형성은 모든 합성곱 계층과 완전 연결 계층의 출력에 적용됩니다.
첫 번째 합성곱 계층은 224×224×3 입력 이미지를 96개의 11×11×3 크기의 커널로 필터링하며, 스트라이드는 4 픽셀입니다(이는 커널 맵에서 인접한 뉴런들의 수용 영역 중심 간의 거리입니다). 두 번째 합성곱 계층은 (응답 정규화되고 풀링된) 첫 번째 합성곱 계층의 출력을 입력으로 받아 256개의 5×5×48 크기의 커널로 필터링합니다. 세 번째, 네 번째, 다섯 번째 합성곱 계층은 풀링이나 정규화 계층 없이 서로 연결되어 있습니다. 세 번째 합성곱 계층은 256개의 (정규화되고 풀링된) 두 번째 합성곱 계층 출력에 연결된 384개의 3×3×256 크기의 커널을 가집니다. 네 번째 합성곱 계층은 384개의 3×3×192 크기의 커널을 가지며, 다섯 번째 합성곱 계층은 256개의 3×3×192 크기의 커널을 가집니다. 완전 연결 계층은 각각 4096개의 뉴런을 포함합니다.
4 과적합 줄이기
우리의 신경망 아키텍처는 6천만 개의 파라미터를 가지고 있습니다. ILSVRC의 1000개 클래스가 각 훈련 예제에 대해 이미지에서 라벨로의 매핑에 10비트의 제약을 부과하지만, 이는 과적합 없이 이 많은 파라미터를 학습하기에는 충분하지 않습니다. 아래에서는 과적합을 방지하기 위해 사용하는 두 가지 주요 방법을 설명합니다.
4.1 데이터 증강
이미지 데이터에서 과적합을 줄이는 가장 쉽고 일반적인 방법은 라벨을 유지한 상태에서 데이터셋을 인위적으로 확장하는 것입니다(예: [25, 4, 5]). 우리는 두 가지 형태의 데이터 증강을 사용했으며, 두 방식 모두 변환된 이미지를 원본 이미지로부터 거의 계산 비용 없이 생성할 수 있어 디스크에 저장할 필요가 없습니다. 우리의 구현에서는 변환된 이미지를 CPU의 Python 코드로 생성하며, GPU는 이전 배치의 이미지를 훈련하는 동안 이를 처리합니다. 따라서 이 데이터 증강 방식은 사실상 계산 비용이 들지 않습니다.
첫 번째 데이터 증강 방식은 이미지의 평행 이동과 수평 반사를 생성하는 것입니다. 우리는 256×256 크기의 이미지에서 무작위로 224×224 크기의 패치를 추출하고(그리고 그 수평 반사본도 포함), 네트워크를 이러한 추출된 패치들로 훈련시킵니다. 이 방식은 훈련 세트 크기를 2048배로 늘리지만, 결과적으로 생성된 훈련 예제들은 상호 의존성이 높습니다. 이 방식이 없다면, 우리의 네트워크는 상당한 과적합에 시달렸을 것이며, 우리는 훨씬 작은 네트워크를 사용해야 했을 것입니다. 테스트 시, 네트워크는 네 가지 모서리 패치와 중앙 패치를 포함한 다섯 개의 224×224 패치를 추출하고, 그들의 수평 반사본도 추출합니다(따라서 총 10개의 패치). 네트워크는 이 10개의 패치에서 소프트맥스 계층의 예측을 평균하여 최종 예측을 만듭니다.

4.2 드롭아웃 (Dropout)
여러 다른 모델의 예측을 결합하는 것은 테스트 오류를 줄이는 매우 성공적인 방법입니다 [1, 3]. 하지만, 이미 훈련에 여러 날이 걸리는 대규모 신경망에서는 이 방식이 너무 비효율적일 수 있습니다. 그러나 모델 결합의 매우 효율적인 버전이 있는데, 이는 훈련 중 약 두 배의 비용만 추가됩니다. 최근 도입된 "드롭아웃" [10]이라는 기술은 각 은닉 뉴런의 출력을 0.5의 확률로 0으로 설정하는 방식입니다. 이 방식으로 "드롭아웃"된 뉴런들은 순방향 계산에 기여하지 않으며 역전파에도 참여하지 않습니다. 따라서 입력이 주어질 때마다 신경망은 다른 아키텍처를 샘플링하지만, 이들 아키텍처는 모두 가중치를 공유합니다. 이 기술은 뉴런들의 복잡한 공동 적응(co-adaptations)을 줄입니다. 왜냐하면 뉴런은 특정 다른 뉴런들의 존재에 의존할 수 없기 때문입니다. 따라서 뉴런은 다른 뉴런들의 다양한 무작위 부분 집합과 함께 사용될 수 있는 더 견고한 특징을 학습해야 합니다.
테스트 시에는 모든 뉴런을 사용하지만, 출력에 0.5를 곱합니다. 이는 지수적으로 많은 드롭아웃 네트워크들이 생성하는 예측 분포의 기하 평균을 취한 것과 비슷한 합리적인 근사값입니다.
우리는 그림 2에서 첫 두 개의 완전 연결 계층에 드롭아웃을 사용했습니다. 드롭아웃 없이 네트워크는 상당한 과적합을 보였습니다. 드롭아웃은 수렴하는 데 필요한 반복 횟수를 대략 두 배로 늘립니다.

그림 3: 224×224×3 크기의 입력 이미지에 대해 첫 번째 합성곱 계층이 학습한 96개의 11×11×3 크기의 합성곱 커널들. 상단 48개의 커널은 GPU 1에서 학습되었고, 하단 48개의 커널은 GPU 2에서 학습되었습니다. 자세한 내용은 6.1절을 참조하세요.
5 학습 세부사항
우리의 모델은 배치 크기 128, 모멘텀 0.9, 가중치 감소(weight decay) 0.0005를 사용하여 확률적 경사 하강법으로 훈련되었습니다. 이 작은 가중치 감소는 모델 학습에 중요하다는 것을 발견했습니다. 즉, 이 가중치 감소는 단순한 정규화 기법이 아니라, 모델의 훈련 오류를 줄이는 역할을 했습니다. 가중치 w에 대한 갱신 규칙은 다음과 같습니다:

각 계층의 가중치는 평균이 0이고 표준편차가 0.01인 가우시안 분포에서 초기화되었습니다. 두 번째, 네 번째, 다섯 번째 합성곱 계층 및 완전 연결 은닉 계층의 뉴런 바이어스는 상수 1로 초기화되었으며, 이는 ReLU에 긍정적인 입력을 제공함으로써 초기 학습 단계를 가속화합니다. 나머지 계층의 뉴런 바이어스는 상수 0으로 초기화되었습니다.
우리는 모든 계층에 동일한 학습률을 사용했으며, 학습 중 수동으로 학습률을 조정했습니다. 우리가 따랐던 기준은 검증 오류율이 현재 학습률에서 더 이상 개선되지 않을 때 학습률을 10분의 1로 줄이는 것이었습니다. 학습률은 초기값으로 0.01로 설정되었고, 종료 전에 세 번 감소시켰습니다. 네트워크는 120만 개의 이미지로 구성된 훈련 세트를 약 90번 순환하면서 훈련되었으며, 이는 두 개의 NVIDIA GTX 580 3GB GPU에서 5~6일이 걸렸습니다.
6 결과
우리의 ILSVRC-2010 결과는 표 1에 요약되어 있습니다. 우리의 네트워크는 테스트 세트에서 top-1 오류율 37.5%, top-5 오류율 17.0%를 달성했습니다. ILSVRC-2010 대회 기간 동안의 최고 성능은 서로 다른 특징들에 대해 훈련된 6개의 희소 코딩 모델의 예측을 평균한 접근 방식으로, top-1 오류율 47.1%, top-5 오류율 28.2%였습니다 [2]. 그 이후로, Fisher 벡터(FVs)로부터 계산된 두 가지 종류의 밀집 샘플링 특징에 대해 훈련된 두 분류기의 예측을 평균한 방법으로 top-1 오류율 45.7%, top-5 오류율 25.7%라는 최고 성능이 발표되었습니다 [24].
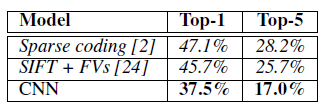
표 1: ILSVRC-2010 테스트 세트에서의 결과 비교. 이탤릭체로 표시된 값은 다른 연구자들이 달성한 최고 성과입니다.
우리는 또한 ILSVRC-2012 대회에 모델을 제출했으며, 그 결과를 표 2에 보고했습니다. ILSVRC-2012 테스트 세트의 라벨은 공개되지 않았기 때문에, 우리가 시도한 모든 모델에 대해 테스트 오류율을 보고할 수는 없습니다. 이 단락의 나머지 부분에서는 검증 오류율과 테스트 오류율을 서로 혼용하여 사용하고 있는데, 우리의 경험에 따르면 이 두 값은 0.1% 이상 차이나지 않습니다(표 2 참조). 이 논문에서 설명한 CNN은 top-5 오류율 18.2%를 달성했습니다. 다섯 개의 유사한 CNN의 예측을 평균하면 오류율이 16.4%로 줄어듭니다. 마지막 풀링 계층 위에 추가로 여섯 번째 합성곱 계층을 가진 CNN을 학습시키고, 이를 ILSVRC-2012 데이터셋에 대해 "미세 조정"했을 때 오류율은 16.6%였습니다. 전체 Fall 2011 ImageNet 릴리즈(1,500만 개 이미지, 22,000개 카테고리)를 사전 훈련(pre-training)한 두 개의 CNN의 예측을 앞서 언급한 다섯 개의 CNN과 평균했을 때, 오류율은 15.3%로 감소했습니다. 두 번째로 좋은 성능을 기록한 참가자는 밀집 샘플링된 여러 종류의 특징에서 계산된 Fisher 벡터(FVs)로 훈련된 여러 분류기의 예측을 평균하는 방식으로 26.2%의 오류율을 달성했습니다 [7].
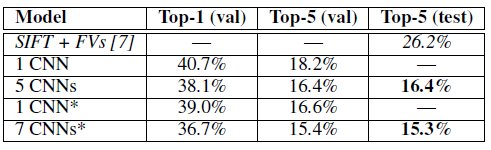
표 2: ILSVRC-2012 검증 및 테스트 세트에서의 오류율 비교. 이탤릭체로 표시된 값은 다른 연구자들이 달성한 최고 성과입니다. 별표(*)가 있는 모델은 전체 2011년 가을 ImageNet 릴리즈를 분류하기 위해 사전 훈련된 모델입니다. 자세한 내용은 6절을 참조하세요.
마지막으로, 우리는 Fall 2009 버전의 ImageNet(10,184개의 카테고리와 890만 개의 이미지)에 대한 오류율도 보고합니다. 이 데이터셋에서는 문헌에 따라 이미지를 절반은 훈련용, 절반은 테스트용으로 사용하는 방식을 따릅니다. 확립된 테스트 세트가 없기 때문에 우리의 데이터 분할은 이전 연구자들이 사용한 분할 방식과 다를 수 있지만, 이로 인해 결과에 큰 차이는 없습니다. 이 데이터셋에서 우리의 top-1 오류율은 67.4%, top-5 오류율은 40.9%이며, 이는 앞서 설명한 네트워크에 마지막 풀링 계층 위에 여섯 번째 합성곱 계층을 추가한 모델로 달성되었습니다. 이 데이터셋에 대한 이전에 발표된 최고 성과는 top-1 오류율 78.1%와 top-5 오류율 60.9%입니다 [19].
6.1 정성적 평가
그림 3은 네트워크의 두 데이터 연결 계층에서 학습된 합성곱 커널들을 보여줍니다. 네트워크는 다양한 주파수와 방향을 선택하는 커널뿐만 아니라 여러 색상의 점(blob)도 학습했습니다. 3.5절에서 설명한 제한된 연결성으로 인해, 두 GPU가 각각 다른 특성을 학습하는 것을 주목할 수 있습니다. GPU 1에서 학습된 커널들은 주로 색상에 무관한 커널인 반면, GPU 2에서 학습된 커널들은 주로 색상에 특정한 커널들입니다. 이러한 종류의 특화 현상은 모든 실행에서 발생하며, 특정 초기 가중치 설정과는 무관합니다(단, GPU의 번호 재지정은 가능합니다).


그림 4: (왼쪽) ILSVRC-2010 테스트 이미지 8개와 모델이 가장 가능성이 높다고 판단한 다섯 개의 라벨들. 각 이미지 아래에 정답 라벨이 적혀 있으며, 정답이 상위 5개의 라벨에 포함될 경우 빨간색 막대로 해당 라벨에 할당된 확률도 표시됩니다. (오른쪽) 첫 번째 열에는 ILSVRC-2010 테스트 이미지 5개가 있습니다. 나머지 열들은 테스트 이미지의 마지막 은닉 계층에서 나온 특징 벡터와 유클리드 거리가 가장 작은 6개의 훈련 이미지를 보여줍니다.
그림 4의 왼쪽 패널에서 우리는 8개의 테스트 이미지에 대한 네트워크의 top-5 예측을 계산하여 네트워크가 학습한 내용을 정성적으로 평가했습니다. 왼쪽 상단에 있는 진드기처럼 중앙에 있지 않은 객체들도 네트워크가 인식할 수 있음을 알 수 있습니다. 대부분의 top-5 라벨은 합리적인 것처럼 보입니다. 예를 들어, 표범에 대해서는 다른 종류의 고양이들만이 타당한 라벨로 간주되었습니다. 일부 경우(그릴, 체리)에는 사진의 초점에 대한 진정한 모호성이 존재합니다.
네트워크의 시각적 지식을 탐구하는 또 다른 방법은 이미지가 마지막 4096차원의 은닉 계층에서 유도한 특징 활성화를 고려하는 것입니다. 만약 두 이미지가 유클리드 거리가 작은 특징 활성화 벡터를 생성한다면, 신경망의 상위 계층은 이 이미지들을 유사하다고 간주할 수 있습니다. 그림 4는 테스트 세트의 5개 이미지와 이 측정에 따라 훈련 세트에서 각 이미지와 가장 유사한 6개의 이미지를 보여줍니다. 주목할 점은 픽셀 수준에서는 가져온 훈련 이미지들이 첫 번째 열의 쿼리 이미지와 L2 거리 상 가까운 것이 아니라는 것입니다. 예를 들어, 가져온 개와 코끼리들은 다양한 자세로 나타납니다. 더 많은 테스트 이미지들에 대한 결과는 추가 자료에서 제시됩니다.
4096차원의 실수 벡터 간의 유클리드 거리를 사용하여 유사성을 계산하는 것은 비효율적이지만, 오토인코더를 훈련시켜 이 벡터들을 짧은 이진 코드로 압축하면 효율적으로 만들 수 있습니다. 이는 원시 픽셀에 오토인코더를 적용하는 것보다 훨씬 더 나은 이미지 검색 방법을 제공할 것입니다 [14]. 원시 픽셀은 이미지 라벨을 사용하지 않기 때문에 의미적으로 유사한지 여부와 관계없이 유사한 에지 패턴을 가진 이미지를 검색하는 경향이 있습니다.
7 논의
우리의 결과는 대규모 깊은 합성곱 신경망이 순수하게 지도 학습을 사용하여 매우 어려운 데이터셋에서 기록적인 성과를 달성할 수 있음을 보여줍니다. 신경망의 성능이 단일 합성곱 계층을 제거하면 저하된다는 점도 주목할 만합니다. 예를 들어, 중간 계층 중 하나를 제거하면 네트워크의 top-1 성능이 약 2% 감소합니다. 따라서 이 깊이가 우리가 달성한 결과에 중요합니다.
실험을 단순화하기 위해, 우리는 비지도 사전 학습을 사용하지 않았습니다. 하지만 사전 학습이 도움이 될 것으로 예상되며, 특히 네트워크 크기를 상당히 늘리면서 라벨이 있는 데이터의 양을 크게 늘리지 못하는 경우에는 더욱 그럴 것입니다. 지금까지 우리의 결과는 네트워크를 더 크게 하고 더 오래 훈련시킬수록 개선되었지만, 인간 시각 시스템의 하부 측두 경로와 일치하려면 아직 많은 도약이 필요합니다. 궁극적으로 우리는 비디오 시퀀스에서 매우 크고 깊은 합성곱 신경망을 사용하고 싶습니다. 비디오의 시간적 구조는 정적 이미지에서 부족하거나 덜 명확한 매우 유용한 정보를 제공합니다.



