https://arxiv.org/abs/2407.13278
Deep Time Series Models: A Comprehensive Survey and Benchmark
Time series, characterized by a sequence of data points arranged in a discrete-time order, are ubiquitous in real-world applications. Different from other modalities, time series present unique challenges due to their complex and dynamic nature, including
arxiv.org
를 살펴보다가 발견
https://github.com/thuml/iTransformer
https://arxiv.org/abs/2310.06625
iTransformer: Inverted Transformers Are Effective for Time Series Forecasting
The recent boom of linear forecasting models questions the ongoing passion for architectural modifications of Transformer-based forecasters. These forecasters leverage Transformers to model the global dependencies over temporal tokens of time series, with
arxiv.org
초록
최근의 선형 예측 모델의 붐은 Transformer 기반 예측기의 구조적 수정에 대한 지속적인 열정을 의문시하고 있습니다. 이러한 예측기들은 시계열 데이터의 시간 토큰 간의 전역 의존성을 모델링하기 위해 Transformer를 활용하며, 각 토큰은 동일한 타임스탬프의 여러 변수로 구성됩니다. 그러나 Transformer는 더 큰 과거 관찰 창(lookback window)을 가진 시계열을 예측하는 데 성능 저하와 계산 복잡성 증가의 문제에 직면해 있습니다. 또한, 각 시간 토큰의 임베딩은 잠재적인 지연 이벤트와 서로 다른 물리적 측정을 나타내는 여러 변수를 결합하는데, 이는 변수 중심의 표현을 학습하는 데 실패할 수 있으며, 의미 없는 주의(attention) 맵을 초래할 수 있습니다.
이 연구에서는 Transformer 구성 요소들의 역할에 대해 재고하고, 기본 구성 요소를 수정하지 않고 Transformer 아키텍처를 재활용하는 방법을 제안합니다. 우리는 iTransformer를 제안하며, 이는 단순히 전치된(inverted) 차원에 대해 주의(attention)와 피드포워드 네트워크를 적용합니다. 구체적으로, 개별 시계열의 시간 지점을 변수 토큰으로 임베딩하고, 주의 메커니즘은 이 변수 토큰들을 활용하여 다변량 상관관계를 캡처합니다. 한편, 피드포워드 네트워크는 각 변수 토큰에 대해 비선형 표현을 학습합니다. iTransformer 모델은 실제 데이터셋에서 최첨단(state-of-the-art) 성능을 달성하며, Transformer 계열 모델의 성능 향상, 다양한 변수들에 대한 일반화 능력, 그리고 임의의 과거 관찰 창을 더 잘 활용할 수 있는 능력을 갖추도록 합니다. 이러한 특징은 시계열 예측의 기본 백본으로서 iTransformer를 좋은 대안으로 만듭니다.
1. 서론

그림 1: iTransformer의 성능. TimesNet (2023)을 따라 평균 결과(MSE)가 보고됩니다.
Transformer(Vaswani et al., 2017)는 자연어 처리(Brown et al., 2020)와 컴퓨터 비전(Dosovitskiy et al., 2021)에서 큰 성공을 거두었으며, 확장 법칙(Kaplan et al., 2020)을 따르는 기초 모델로 성장해 왔습니다. 이러한 광범위한 분야에서의 큰 성공에 영감을 받아, 쌍방 의존성을 묘사하고 시퀀스에서 다중 수준 표현을 추출하는 강력한 능력을 가진 Transformer는 시계열 예측에서도 두각을 나타내고 있습니다(Li et al., 2021; Wu et al., 2021; Nie et al., 2023).
하지만 최근 연구자들은 Transformer 기반 예측기의 타당성에 대해 의문을 제기하기 시작했습니다. 이는 일반적으로 동일한 타임스탬프의 여러 변수를 구분 불가능한 채널로 임베딩하고, 이러한 시간 토큰에 주의를 적용하여 시간 의존성을 캡처합니다. 시간 지점 간의 수치적이지만 덜 의미 있는 관계를 고려했을 때, 연구자들은 통계적 예측기까지 거슬러 올라갈 수 있는 단순한 선형 레이어가 성능과 효율성 모두에서 복잡한 Transformer를 능가한다고 발견했습니다(Zeng et al., 2023; Das et al., 2023). 동시에, 변수의 독립성을 보장하고 상호 정보를 활용하는 것은 명확하게 다변량 상관관계를 모델링하여 정확한 예측을 달성하려는 최근 연구에 의해 더욱 강조되고 있지만(Zhang & Yan, 2023; Ekambaram et al., 2023), 이는 기존 Transformer 아키텍처를 완전히 뒤집지 않고서는 거의 달성하기 어려운 목표입니다.
Transformer 기반 예측기에 대한 논란을 고려할 때, 우리는 왜 Transformer가 다른 많은 분야에서는 주로 사용되면서 시계열 예측에서는 오히려 선형 모델보다 성능이 떨어지는지에 대해 고민해 보았습니다. 기존 Transformer 기반 예측기의 구조가 다변량 시계열 예측에는 적합하지 않을 수 있다는 점을 주목하게 되었습니다. 그림 2의 상단에 나타난 바와 같이, 기본적으로 불일치한 측정값에 의해 기록된 완전히 다른 물리적 의미를 나타내는 동일한 시간 단계의 포인트들이 하나의 토큰으로 임베딩되어 다변량 상관관계가 사라집니다. 그리고 단일 시간 단계로 형성된 토큰은 지나치게 국소적인 수용 영역과 시간 정렬이 맞지 않는 이벤트를 나타내어 유용한 정보를 드러내는 데 어려움을 겪을 수 있습니다. 또한, 시계열 변동이 시퀀스 순서에 크게 영향을 받을 수 있는 상황에서도 순서에 불변한 주의 메커니즘이 부적절하게 시간 차원에 적용됩니다(Zeng et al., 2023). 그 결과, Transformer는 필수적인 시계열 표현을 포착하고 다변량 상관관계를 묘사하는 데 약해지며, 다양한 시계열 데이터에서 그 용량과 일반화 능력이 제한됩니다.
타임스탬프의 다변량 포인트를 하나의 시간 토큰으로 임베딩하는 잠재적 위험을 고려하여, 우리는 시계열을 반전시켜 각 변수를 독립적으로 전체 시계열을 (변수) 토큰으로 임베딩하는 방식을 채택했습니다. 이는 국소 수용 영역을 확장하는 Patching(Nie et al., 2023)의 극단적인 사례입니다. 반전함으로써, 임베딩된 토큰은 다변량 상관관계를 위해 부흥하는 주의 메커니즘에 의해 더 잘 활용될 수 있는, 보다 변수 중심적인 글로벌 표현을 집계합니다. 한편, 피드포워드 네트워크는 임의의 과거 시계열로부터 인코딩된 변수들에 대해 일반화 가능한 표현을 학습하고, 이를 통해 미래 시계열을 예측하는 데 충분한 능력을 발휘할 수 있습니다.
이상의 동기를 바탕으로, Transformer가 시계열 예측에 비효과적이라는 것이 아니라 제대로 사용되지 않았음을 믿게 되었습니다. 본 논문에서는 Transformer 구조를 재검토하고 iTransformer를 시계열 예측의 기본 백본으로 제안합니다. 기술적으로는, 각 시계열을 변수 토큰으로 임베딩하고, 다변량 상관관계를 위한 주의를 채택하며, 시계열 표현을 위해 피드포워드 네트워크를 사용합니다. 실험적으로, 제안된 iTransformer는 그림 1에 제시된 실제 예측 벤치마크에서 최첨단 성능을 달성하며, Transformer 기반 예측기의 고질적인 문제점을 해결합니다. 우리의 기여는 세 가지 측면에서 요약됩니다:

그림 2: 기존 Transformer(상단)과 제안된 iTransformer(하단)의 비교. Transformer는 각 시간 단계의 다변량 표현을 포함하는 시간 토큰을 임베딩합니다. iTransformer는 각 시계열을 독립적으로 변수 토큰으로 임베딩하여 주의 모듈이 다변량 상관관계를 묘사하고 피드포워드 네트워크가 시계열 표현을 인코딩할 수 있도록 합니다.
• 우리는 Transformer의 아키텍처를 재고하고, 다변량 시계열에서 기존 Transformer 구성 요소의 유능한 능력이 충분히 탐구되지 않았음을 밝혀냈습니다.
• 우리는 독립된 시계열을 토큰으로 간주하여 자체 주의 메커니즘을 통해 다변량 상관관계를 포착하고, 계층 정규화와 피드포워드 네트워크 모듈을 활용하여 시계열 예측을 위한 더 나은 시리즈-글로벌 표현을 학습하는 iTransformer를 제안합니다.
• 실험적으로, iTransformer는 실제 벤치마크에서 포괄적인 최첨단 성능을 달성합니다. 우리는 반전된 모듈과 아키텍처 선택을 광범위하게 분석하여 Transformer 기반 예측기의 향후 개선 방향에 대한 유망한 경로를 제시합니다.
2. 관련 연구
자연어 처리 및 컴퓨터 비전 분야에서의 점진적인 돌파구와 함께, 정교하게 설계된 Transformer 변형 모델들이 보편적인 시계열 예측 응용을 해결하기 위해 제안되었습니다. 동시대의 TCN(Bai et al., 2018; Liu et al., 2022a)과 RNN 기반 예측기(Zhao et al., 2017; Rangapuram et al., 2018; Salinas et al., 2020)를 넘어서, Transformer는 강력한 시퀀스 모델링 능력과 유망한 모델 확장성을 보여주었으며, 이는 시계열 예측을 위해 적응된 열정적인 수정의 트렌드를 이끌었습니다.
Transformer 기반 예측기에 대한 체계적인 리뷰를 통해, 기존 수정은 구성 요소 및 아키텍처를 수정하는지 여부에 따라 네 가지 범주로 나눌 수 있음을 결론지었습니다. 그림 3에 나타난 것처럼, 첫 번째 범주(Wu et al., 2021; Li et al., 2021; Zhou et al., 2022)는 가장 일반적인 접근으로, 주로 구성 요소의 적응에 관한 것이며, 특히 시간적 의존성 모델링을 위한 주의(attention) 모듈과 긴 시퀀스의 복잡도 최적화에 중점을 둡니다. 하지만 선형 예측기(Oreshkin et al., 2019; Zeng et al., 2023; Das et al., 2023; Liu et al., 2023)의 급속한 등장과 함께, 뛰어난 성능과 효율성은 이 방향에 지속적인 도전을 가하고 있습니다. 그 후 두 번째 범주는 Transformer를 충분히 활용하려고 시도합니다. 이는 시계열의 고유한 처리를 더 주목하는데, 예를 들어 정상화(Stationarization)(Liu et al., 2022b), 채널 독립성(Channel Independence), 그리고 패칭(Patching)(Nie et al., 2023)과 같은 접근이 일관된 성능 향상을 가져왔습니다. 게다가, 다변량의 독립성과 상호작용의 중요성이 증가하면서, 세 번째 범주는 구성 요소와 아키텍처 양면에서 Transformer를 개조합니다. 대표적인 연구(Zhang & Yan, 2023)는 갱신된 주의 메커니즘과 아키텍처를 통해 시간 간 및 변수 간 의존성을 명시적으로 포착합니다.
기존 연구들과 달리, iTransformer는 Transformer의 기본 구성 요소를 전혀 수정하지 않습니다. 대신, 반전된 차원에서 구성 요소를 채택하고 수정된 아키텍처를 사용하며, 현재까지 알려진 바에 따르면 네 번째 범주에 속하는 유일한 사례입니다. 우리는 이 구성 요소들의 능력이 광범위하게 테스트를 견뎌왔음을 믿으며, 실제 문제는 Transformer의 아키텍처가 부적절하게 채택되었다는 점이라고 생각합니다.

그림 3: 구성 요소 및 아키텍처 수정에 따라 분류된 Transformer 기반 예측기.
3. iTransformer
다변량 시계열 예측
다변량 시계열 예측에서, 주어진 과거 관찰 값 $$\mathbf{X} = \{\mathbf{x}_1, \dots, \mathbf{x}_T\} \in \mathbb{R}^{T \times N}$$ (여기서 \(T\)는 시간 단계 수, \(N\)은 변수 수)로부터 향후 \(S\) 단계 동안의 값을 예측합니다.
예측할 미래 값은 다음과 같이 정의됩니다: $$\mathbf{Y} = \{\mathbf{x}_{T+1}, \dots, \mathbf{x}_{T+S}\} \in \mathbb{R}^{S \times N}$$.
편의를 위해, \(\mathbf{X}_{t, :}\) 은 시간 단계 \(t\)에서 동시에 기록된 시간 지점을 나타내며, \(\mathbf{X}_{:, n}\) 은 각 변수 \(n\)에 대한 전체 시계열을 나타냅니다.
주목할 점은 데이터셋의 변수들 간 체계적인 시간 지연으로 인해 \(\mathbf{X}_{t, :}\) 이 실제 시나리오에서 동일한 사건을 반영하는 시간을 포함하지 않을 수 있다는 것입니다.
또한, \(\mathbf{X}_{t, :}\) 의 요소들은 물리적 측정과 통계적 분포가 서로 다를 수 있으며, 이는 일반적으로 변수 \(\mathbf{X}_{:, n}\) 과 관련이 있습니다.
3.1 구조 개요
그림 4에 설명된 제안된 iTransformer는 Transformer(Vaswani et al., 2017)의 인코더만을 채택한 아키텍처를 사용하며, 임베딩, 투영, Transformer 블록을 포함합니다.

그림 4: iTransformer의 전체 구조. Transformer의 인코더와 동일한 모듈 배열을 공유합니다. (a) 다양한 변수의 원시 시계열을 독립적으로 토큰으로 임베딩합니다. (b) 다변량 상관관계를 나타내는 해석 가능성이 강화된 상태에서 자기 주의를 임베딩된 변수 토큰에 적용합니다. (c) 각 토큰의 시계열 표현은 공유 피드포워드 네트워크에 의해 추출됩니다. (d) 계층 정규화를 채택하여 변수 간 차이를 줄입니다.
전체 시계열을 토큰으로 임베딩
대부분의 Transformer 기반 예측기는 일반적으로 동일한 시간의 여러 변수를 (시간) 토큰으로 간주하고 예측 작업의 생성적 공식화에 따릅니다. 그러나 우리는 수치적 방식에서의 접근이 주의 맵을 학습하는 데 덜 유익할 수 있음을 발견했으며, 이는 관련 필드를 확장하는 Patching(Dosovitskiy et al., 2021; Nie et al., 2023)의 증가하는 응용으로 뒷받침됩니다. 한편, 선형 예측기의 성공은 토큰 생성을 위해 무거운 인코더-디코더 Transformer를 채택할 필요성에 도전합니다. 대신, 제안된 인코더만 사용하는 iTransformer는 다변량 시계열의 표현 학습과 적응적 상관에 초점을 맞춥니다. 기본적으로 복잡한 과정에 의해 구동되는 각 시계열은 먼저 변수의 특성을 설명하기 위해 토큰화되고, 상호작용을 위해 자기 주의가 적용되며, 각 시계열 표현을 위해 피드포워드 네트워크에 의해 개별적으로 처리됩니다. 특히, 예측 시계열을 생성하는 작업은 본질적으로 선형 레이어에 전달되며, 이는 이전 연구(Das et al., 2023)에 의해 능력을 입증하였으며, 다음 섹션에서 자세한 분석을 제공합니다.
iTransformer 예측 과정 공식화
위의 고려 사항을 바탕으로, iTransformer에서는 특정 변수 \(\hat{Y}_n\)의 미래 시계열을 \(X_n\)을 기반으로 예측하는 과정을 다음과 같이 간단히 공식화합니다:
여기서 \( H = \{ h_1, \dots, h_N \} \in \mathbb{R}^{N \times D} \) 는 차원 \( D \)의 \( N \)개의 임베딩된 토큰을 포함하며, 윗첨자는 레이어 인덱스를 나타냅니다.
임베딩 \( \mathbb{R}^T \rightarrow \mathbb{R}^D \) 및 투영 \( \mathbb{R}^D \rightarrow \mathbb{R}^S \) 는 모두 다층 퍼셉트론 (MLP)에 의해 구현됩니다.
얻어진 변수 토큰은 자기 주의에 의해 상호작용하며, 각 TrmBlock에서 공유된 피드포워드 네트워크에 의해 독립적으로 처리됩니다.
특히, 피드포워드 네트워크의 뉴런 순열에서 시퀀스 순서가 암시적으로 저장되기 때문에, 기존 Transformer의 위치 임베딩은 여기에서 더 이상 필요하지 않습니다.
iTransformers
이 아키텍처는 다변량 상관관계를 위한 주의가 적용된다는 점 외에는 Transformer 변형에 대해 더 이상의 특정 요구사항을 전제하지 않습니다. 따라서 효율적인 주의 메커니즘 모음(Li et al., 2021; Wu et al., 2022; Dao et al., 2022)이 플러그인으로 사용될 수 있으며, 변량 수가 증가할 때 복잡성을 줄일 수 있습니다. 또한, 주의의 입력 유연성을 통해 학습에서 추론까지 토큰 수를 다르게 할 수 있으며, 모델은 임의의 변수 수로 학습될 수 있습니다. 반전된 Transformer인 iTransformers는 4.2 섹션의 실험에서 광범위하게 평가되었으며 시계열 예측에서의 장점을 입증합니다.
3.2 반전된 Transformer 구성 요소
우리는 층 정규화(layer normalization), 피드포워드 네트워크, 자기 주의(self-attention) 모듈로 구성된 L 개의 블록을 쌓아서 구성합니다. 그러나 반전된 차원에서 이들의 역할은 신중히 재고되었습니다.
층 정규화
층 정규화(Ba et al., 2016)는 원래 심층 네트워크의 수렴성과 학습 안정성을 높이기 위해 제안되었습니다. 일반적인 Transformer 기반 예측기에서 이 모듈은 동일한 타임스탬프의 다변량 표현을 정규화하여 점차적으로 변수들을 상호 결합합니다. 수집된 시간 지점이 동일한 사건을 나타내지 않을 경우, 이 작업은 인과성이 없는 과정 또는 지연된 과정 간의 상호작용 잡음을 도입할 수 있습니다. 반전된 버전에서는 개별 변수의 시계열 표현에 정규화를 적용하는데(수식 2와 같이), 이는 비정상적 문제를 해결하는 데 효과적임이 입증되었습니다(Kim et al., 2021; Liu et al., 2022b). 또한, 모든 시계열이 (변수) 토큰으로 가우시안 분포로 정규화되기 때문에, 불일치한 측정값으로 인한 차이를 줄일 수 있습니다. 반대로, 이전 아키텍처에서는 시간 단계의 서로 다른 토큰들이 정규화되므로 시계열이 지나치게 부드러워질 수 있었습니다.

피드포워드 네트워크
Transformer는 피드포워드 네트워크(FFN)를 토큰 표현을 인코딩하는 기본 빌딩 블록으로 채택하며, 각 토큰에 동일하게 적용됩니다. 앞서 언급했듯이, 기존 Transformer에서 동일한 타임스탬프의 여러 변수가 형성하는 토큰은 잘못된 위치에 있을 수 있고 지나치게 국소화되어 있어 예측에 충분한 정보를 드러내지 못할 수 있습니다. 반전된 버전에서는 FFN이 각 변수 토큰의 시계열 표현에 적용됩니다. 보편 근사 정리(Hornik, 1991)에 따라 FFN은 시계열을 설명하는 복잡한 표현을 추출할 수 있습니다. 반전된 블록의 스택을 통해, FFN은 관찰된 시계열을 인코딩하고 미래 시계열을 위한 표현을 해독하는 데 전념하며, 이는 최근 완전히 MLP(다층 퍼셉트론) 기반으로 구축된 연구에서 효과적으로 작동하고 있습니다(Tolstikhin et al., 2021; Das et al., 2023).
더 흥미로운 점은 독립된 시계열에서의 동일한 선형 작업이 최근의 선형 예측기(Zeng et al., 2023)와 채널 독립성(Nie et al., 2023)의 결합으로 작용한다는 것입니다. 이는 시계열 표현을 이해하는 데 유익할 수 있습니다. 선형 예측기에 대한 최근의 재조명(Li et al., 2023)은 MLP가 추출한 시간적 특징이 서로 다른 시계열에서 공유되어야 함을 강조합니다. 우리는 MLP의 뉴런들이 시계열의 본질적인 속성, 예를 들어 진폭, 주기성, 심지어 주파수 스펙트럼(뉴런을 필터로 간주)을 묘사하도록 학습된다는 합리적인 설명을 제안합니다. 이는 시간 지점에 적용된 자기 주의보다 더 유리한 예측 표현 학습자로서 작용합니다. 실험적으로, 우리는 섹션 4.3에서 선형 계층의 이점을 누리는 데 도움이 되는 노동의 분할을 검증했으며, 더 큰 과거 시계열을 제공할 때 향상된 성능과 보지 못한 변수에 대한 일반화 능력을 포함합니다.
자기 주의(Self-attention)
자기 주의(Self-attention)
주의 메커니즘은 이전 예측기에서 시간적 의존성 모델링을 촉진하기 위해 일반적으로 채택되었지만, 반전된 모델은 하나의 변수 전체 시계열을 독립적인 과정으로 간주합니다. 구체적으로, 각 시계열의 종합적으로 추출된 표현 $$ \mathbf{H} = \{ \mathbf{h}_0, \dots, \mathbf{h}_N \} \in \mathbb{R}^{N \times D} $$ 을 가지고, 자기 주의 모듈은 선형 투영을 사용하여 쿼리, 키, 값 $$ \mathbf{Q}, \mathbf{K}, \mathbf{V} \in \mathbb{R}^{N \times d_k} $$ 를 얻습니다. 여기서 \( d_k \)는 투영된 차원입니다.
특정 쿼리와 키를 \( \mathbf{q}_i, \mathbf{k}_j \in \mathbb{R}^{d_k} \)로 표기하면, Pre-Softmax 점수의 각 항목은 다음과 같이 표현됩니다:
각 토큰이 그 특징 차원에서 이전에 정규화되었기 때문에, 항목들은 어느 정도 변수 간 상관관계를 나타낼 수 있으며, 전체 점수 맵 $$ \mathbf{A} \in \mathbb{R}^{N \times N} $$ 은 쌍으로 된 변수 토큰 간의 다변량 상관관계를 나타냅니다.
결과적으로, 상관관계가 높은 변수는 다음 표현 상호작용에서 값 \( \mathbf{V} \)와 함께 더 많은 가중치를 가지게 됩니다. 이러한 직관을 바탕으로 제안된 메커니즘은 다변량 시계열 예측에 대해 더 자연스럽고 해석 가능하다고 생각됩니다. 우리는 섹션 4.3과 부록 E.1에서 점수 맵에 대한 시각적 분석을 추가로 제공합니다.
4. 실험
우리는 제안된 iTransformer를 다양한 시계열 예측 응용 프로그램에서 철저히 평가하고, 제안된 프레임워크의 일반성을 검증하며, 시계열의 반전된 차원에서 Transformer 구성 요소를 적용하는 효과를 더욱 깊이 탐구합니다.
데이터셋
우리는 실험에서 7개의 실제 데이터셋을 광범위하게 포함하였으며, 여기에는 ECL, ETT(4개의 하위 집합), Exchange, Traffic, Weather(이들은 Autoformer(Wu et al., 2021)에서 사용됨), Solar-Energy(LSTNet(Lai et al., 2018)에서 제안됨), 그리고 SCINet(Liu et al., 2022a)에서 평가된 PEMS(4개의 하위 집합)가 포함됩니다. 또한, 부록 F.4에서는 Market(6개의 하위 집합)에 대한 실험 결과도 제공합니다. 이 데이터셋은 수백 개의 변수를 가진 Alipay 온라인 거래 애플리케이션의 분 단위 샘플링 서버 부하를 기록하며, 우리는 다른 기준 모델을 일관되게 능가하였습니다. 데이터셋의 자세한 설명은 부록 A.1에 제공되어 있습니다.
4.1 예측 결과
이 섹션에서는 제안된 모델의 예측 성능을 고급 예측기들과 함께 평가하기 위한 광범위한 실험을 수행합니다.
기준 모델(Baselines)
우리는 벤치마크로 10개의 잘 알려진 예측 모델을 신중하게 선택하였습니다. 여기에는 다음이 포함됩니다: (1) Transformer 기반 방법: Autoformer(Wu et al., 2021), FEDformer(Zhou et al., 2022), Stationary(Liu et al., 2022b), Crossformer(Zhang & Yan, 2023), PatchTST(Nie et al., 2023); (2) 선형 기반 방법: DLinear(Zeng et al., 2023), TiDE(Das et al., 2023), RLinear(Li et al., 2023); (3) TCN 기반 방법: SCINet(Liu et al., 2022a), TimesNet(Wu et al., 2023).
주요 결과(Main results)
종합적인 예측 결과는 표 1에 나와 있으며, 가장 좋은 결과는 빨간색으로, 두 번째로 좋은 결과는 밑줄로 표시되어 있습니다. 더 낮은 MSE/MAE는 더 정확한 예측 결과를 의미합니다. 다른 예측기들과 비교했을 때, iTransformer는 특히 고차원 시계열 예측에서 우수한 성능을 보입니다. 또한, 이전 최첨단 모델인 PatchTST는 PEMS의 여러 사례에서 실패하였는데, 이는 데이터셋의 매우 변동이 심한 시계열 때문일 수 있으며, PatchTST의 패칭 메커니즘이 급격한 변동을 처리하는 데 있어 특정 지역성에 초점을 잃을 수 있기 때문입니다. 반면, 제안된 모델은 시계열 표현을 위해 전체 시계열 변동을 집계하므로 이러한 상황에 더 잘 대처할 수 있습니다. 주목할 점은 다변량 상관관계를 명시적으로 포착하는 대표 모델인 Crossformer의 성능이 여전히 iTransformer에 미치지 못하는데, 이는 서로 다른 다변량에서 시간 정렬이 맞지 않는 패치들의 상호작용이 예측에 불필요한 잡음을 초래할 수 있음을 나타냅니다. 따라서, 기존 Transformer 구성 요소는 시간적 모델링과 다변량 상관에 충분히 유능하며, 제안된 반전 아키텍처는 실제 시계열 예측 시나리오를 효과적으로 처리할 수 있습니다.
표 1: 다변량 예측 결과
예측 길이 S∈{12,24,36,48}은 PEMS에 대해, 그리고 S∈{96,192,336,720}은 다른 데이터셋에 대해 적용되었으며, 고정된 과거 관찰 길이 T=96니다. 결과는 모든 예측 길이에 대해 평균화되었습니다. 'Avg'는 하위 집합들에 대해 추가적으로 평균화된 값을 의미합니다. 전체 결과는 부록 F.4에 나와 있습니다.

-----
이 표에서는 7개의 다양한 시계열 데이터셋에 대해 각 모델의 성능을 MSE(평균 제곱 오차)와 MAE(평균 절대 오차)로 평가하고 있습니다. 낮은 MSE와 MAE 값이 더 나은 예측 성능을 나타냅니다.
1. ECL 데이터셋
- iTransformer의 MSE와 MAE는 각각 0.178과 0.270으로, 다른 모델들보다 낮아 가장 우수한 성능을 보였습니다. 특히 RLinear, PatchTST, Crossformer보다 성능이 뛰어나며, 이는 iTransformer가 고차원 데이터에서도 효과적으로 예측할 수 있음을 보여줍니다.
- TimesNet은 MSE 0.192로 두 번째로 좋은 성능을 보였으며, RLinear(MSE 0.219)와 PatchTST(MSE 0.216)는 유사한 수준을 보였습니다.
2. ETT 데이터셋 (평균)
- iTransformer의 MSE는 0.383, MAE는 0.399로 RLinear(MSE 0.380, MAE 0.392)와 매우 비슷한 성능을 보였으며, 두 모델 모두 이 데이터셋에서 뛰어난 성능을 보였습니다.
- 반면 SCINet과 FEDformer는 상대적으로 높은 MSE를 보여 iTransformer가 특히 긴 시계열 예측에서도 강점을 나타낸다는 점을 알 수 있습니다.
3. Exchange 데이터셋
- iTransformer는 MSE 0.360, MAE 0.403으로 RLinear와 PatchTST보다 좋은 성능을 보였습니다.
- PatchTST와 TiDE는 서로 유사한 성능을 보였으며, SCINet은 비교적 성능이 저조했습니다(MSE 0.750).
- TimesNet의 성능도 나쁘지 않지만(MSE 0.416), iTransformer와는 차이가 있음을 확인할 수 있습니다.
4. Traffic 데이터셋
- iTransformer는 MSE 0.428, MAE 0.282로 이 데이터셋에서도 가장 좋은 성능을 보였습니다.
- 반면 RLinear(MSE 0.626)와 PatchTST(MSE 0.555)는 상대적으로 더 높은 MSE를 보여, 특히 변동성이 크고 데이터가 복잡한 시계열에서 iTransformer가 더 강력함을 보여줍니다.
- FEDformer와 SCINet은 이 데이터셋에서 성능이 다소 낮았습니다.
5. Weather 데이터셋
- 이 데이터셋에서도 iTransformer가 우수한 성능을 보였습니다(MSE 0.258, MAE 0.279). PatchTST와 TiDE도 유사한 수준의 성능을 보였지만, 여전히 iTransformer가 가장 낮은 MSE를 기록했습니다.
- Stationary와 Autoformer는 상대적으로 높은 MAE를 보여 복잡한 환경에서의 예측력이 떨어지는 것으로 보입니다.
6. Solar-Energy 데이터셋
- iTransformer의 MSE와 MAE는 각각 0.233과 0.262로 다른 모델들에 비해 월등히 낮았습니다.
- RLinear(MSE 0.369)와 PatchTST(MSE 0.270)는 더 높은 MSE를 보였으며, SCINet과 FEDformer는 특히 높은 MSE를 보여 복잡한 에너지 소비 패턴을 예측하는 데 약점을 보였습니다.
7. PEMS 데이터셋 (평균)
- iTransformer는 MSE 0.119, MAE 0.218로 이 데이터셋에서도 가장 우수한 성능을 나타냈습니다. SCINet(MSE 0.121)도 좋은 성능을 보였으나, PatchTST와 TiDE는 상대적으로 낮은 성능을 보였습니다.
- TimesNet과 FEDformer는 이 데이터셋에서 MSE가 0.148, 0.151로 iTransformer보다는 성능이 떨어집니다.
종합적인 분석
- iTransformer의 강점
- 고차원 시계열 예측에서 특히 뛰어난 성능을 보였습니다. 다양한 데이터셋에서 consistently 높은 예측 정확도를 기록했으며, 특히 복잡한 변동성이나 많은 변수를 포함하는 데이터셋에서 다른 모델들보다 월등히 나은 결과를 보였습니다.
- 대부분의 경우에서 기준 모델들보다 낮은 MSE와 MAE를 기록함으로써 더 높은 정확성과 안정성을 나타냈습니다.
- PatchTST와 Crossformer의 한계
- PatchTST는 데이터셋에 따라 성능의 편차가 크며, 특히 변동성이 큰 데이터셋에서는 iTransformer보다 예측력이 떨어졌습니다. 이는 패치 메커니즘이 급격한 변동을 다루기 어려움을 의미합니다.
- Crossformer는 명시적으로 다변량 상관관계를 포착하지만, 다른 다변량에서 시간 정렬이 맞지 않는 패치들이 상호작용할 때 불필요한 잡음을 초래할 수 있음을 보여주었습니다.
- 선형 모델 대비 성능
- RLinear, DLinear, TiDE와 같은 선형 기반 모델들은 간단하면서도 특정 데이터셋에서는 우수한 성능을 보였지만, iTransformer가 대부분의 데이터셋에서 이를 능가하는 결과를 보였습니다.
- 이는 iTransformer가 더 복잡한 비선형 상호작용을 잘 학습하고, 고차원 데이터를 처리하는 데 있어 더 나은 성능을 발휘한다는 점을 의미합니다.
결론적으로, iTransformer는 다양한 시계열 데이터셋에서 고도의 예측 정확도를 유지하며, 특히 복잡한 다변량 상호작용을 잘 모델링함으로써 기존의 최신 모델들보다 뛰어난 성능을 보여주었습니다.
-----
4.2 iTransformer의 일반성
이 섹션에서는 iTransformer 프레임워크를 Transformer 및 그 변형 모델에 적용하여 평가합니다. 이 모델들은 일반적으로 자기 주의(self-attention) 메커니즘의 이차 복잡성을 해결하는 데 중점을 두며, Reformer(Kitaev et al., 2020), Informer(Li et al., 2021), Flowformer(Wu et al., 2022), FlashAttention(Dao et al., 2022)을 포함합니다. 놀랍고 유망한 결과가 나타났으며, 이는 단순한 반전된 관점이 Transformer 기반 예측기들의 성능을 향상시키고 효율성, 미지의 변수에 대한 일반화, 과거 관찰 데이터를 더 잘 활용하는 능력을 증진할 수 있음을 시사합니다.
성능 향상
우리는 Transformer 및 해당 iTransformer의 성능을 평가하였으며, 표 2에 보고된 성능 향상 결과를 제시합니다. 주목할 점은 프레임워크가 다양한 Transformer 모델을 일관되게 개선한다는 것입니다. 전반적으로 Transformer에서 평균 38.9%, Reformer에서 36.1%, Informer에서 28.5%, Flowformer에서 16.8%, 그리고 Flashformer에서 32.2%의 성능 향상을 달성하였으며, 이는 시계열 예측에서 기존 Transformer 아키텍처의 잘못된 사용을 드러냅니다. 또한, 반전된 구조에서는 주의 메커니즘이 변수 차원에 적용되기 때문에, 선형 복잡성을 가진 효율적인 주의 메커니즘의 도입이 다변량이 많은 경우 발생하는 계산 문제를 본질적으로 해결합니다. 이는 실제 응용에서 일반적으로 발생하는 문제이며, 채널 독립성(Channel Independence)(Nie et al., 2023)에 있어 자원 소모적인 특성을 가질 수 있습니다. 따라서 iTransformer의 아이디어는 Transformer 기반 예측기에 효율적인 주의 메커니즘을 활용할 수 있도록 광범위하게 적용될 수 있습니다.
표 2: 우리의 반전된 프레임워크에 의해 얻어진 성능 향상
Flashformer는 하드웨어 가속된 FlashAttention이 장착된 Transformer를 의미합니다(Dao et al., 2022). 우리는 평균 성능과 상대적인 MSE 감소(성능 향상)를 보고합니다. 전체 결과는 부록 F.2에서 확인할 수 있습니다.

-----
이 표에서는 Transformer 및 다양한 변형 모델들에 대해 원래 모델과 반전(iTransformer 적용) 버전의 성능을 비교하고, 그 성능 향상도를 %로 나타내고 있습니다. 주요 지표로는 MSE(평균 제곱 오차)와 MAE(평균 절대 오차)를 사용하며, 낮을수록 더 나은 성능을 의미합니다.
1. ECL 데이터셋
- Transformer 원래 버전은 MSE 0.277, MAE 0.372였으며, 반전된 버전은 MSE 0.178, MAE 0.270으로 각각 35.6%, 27.4%의 향상을 보였습니다. 이는 반전 구조가 이 모델의 성능을 크게 개선함을 보여줍니다.
- Reformer의 경우, 원래 모델의 MSE는 0.338이었으나, 반전 구조를 도입한 후 0.208로 약 38.4%의 성능 향상을 기록했습니다. MAE 또한 28.7% 향상되었습니다.
- Flashformer의 경우에도 MSE가 0.285에서 0.206으로, 약 27.8%의 향상이 있었으며 MAE 역시 22.9% 개선되었습니다. 이는 반전 구조가 특히 다변량 시계열의 정밀도를 높이는 데 효과적임을 시사합니다.
2. Traffic 데이터셋
- Transformer 원래 버전의 MSE는 0.665, MAE는 0.363으로 기록되었으며, 반전 구조를 적용한 후에는 MSE 0.428, MAE 0.282로 각각 35.6%, 22.3%의 향상을 보였습니다. 이는 특히 복잡한 도로 교통 데이터에서도 iTransformer가 더 높은 예측력을 발휘한다는 것을 보여줍니다.
- Flowformer의 경우, 반전된 버전에서 MSE가 0.524로 30.1% 향상되었고, MAE는 15.6% 개선되었습니다. 이는 Flowformer가 반전 구조에서 더욱 효율적으로 시계열을 모델링할 수 있음을 의미합니다.
- 반면 Flashformer는 MSE가 25.2% 개선되었으나 MAE의 개선폭은 6.4%로, MAE 성능 향상이 다른 모델들에 비해 비교적 적었습니다. 이는 데이터의 복잡성에 따른 MAE 개선의 한계일 수 있습니다.
3. Weather 데이터셋
- Transformer 원래 버전은 MSE 0.657, MAE 0.572였으며, 반전된 구조 적용 후에는 MSE가 0.258, MAE가 0.279로 각각 60.2%, 50.8%의 큰 성능 향상을 보였습니다. 이는 날씨 데이터와 같은 특정 시간적 특성을 강하게 가진 데이터에서 반전 구조가 매우 효과적임을 보여줍니다.
- Reformer의 경우 MSE가 0.803에서 0.248로 약 69.2%의 성능 향상을 기록했습니다. MAE 역시 55.5% 개선되었는데, 이는 반전 구조가 긴 시계열을 다루는 데 특히 강력함을 의미합니다.
- Flowformer의 경우 원래 버전의 MSE는 0.286, MAE는 0.308이었으며, 반전 후 MSE는 0.266으로 7.2%, MAE는 7.7% 개선되었습니다. 이는 이 모델이 이미 고성능이었기 때문에 추가적인 향상의 폭이 작았음을 시사합니다.
- Flashformer는 MSE 0.659에서 0.262로, 60.2%의 향상을 기록했으며, MAE도 50.8% 개선되었습니다. 이 역시 반전 구조가 모델 성능을 대폭 개선하는 것을 보여줍니다.
종합적인 분석
- 전반적인 성능 향상
- 모든 모델에서 iTransformer의 반전 구조를 적용했을 때 성능이 크게 향상되었음을 확인할 수 있습니다. 특히 ECL과 Weather 데이터셋에서는 성능 향상의 폭이 매우 컸으며, 이는 복잡한 다변량 특성이나 계절적 변동이 중요한 데이터에서 반전 구조가 더 효율적인 표현을 학습할 수 있음을 의미합니다.
- 모델별 성능 향상
- Reformer와 Transformer는 반전 구조의 도입으로 가장 큰 성능 향상을 보였으며, 이는 기존 자기 주의 메커니즘이 반전 구조와 결합되었을 때 더욱 효율적으로 시계열을 모델링할 수 있음을 보여줍니다.
- Flowformer의 경우 원래 모델 자체가 이미 효율적인 구조로 설계되어 있어, 반전 구조 도입 후의 향상폭이 다른 모델들에 비해 작았으나 여전히 의미 있는 성능 개선이 있었습니다.
- Flashformer도 모든 데이터셋에서 향상된 성능을 기록했으며, 이는 하드웨어 가속 기능과 반전 구조의 결합이 실시간 응용에서도 큰 도움이 될 수 있음을 시사합니다.
- MSE와 MAE의 개선 폭 비교
- 모든 모델에서 MSE와 MAE가 함께 개선되었지만, 데이터셋과 모델에 따라 MAE의 개선 폭이 다소 작은 경우도 있었습니다. 이는 절대 오차 기준이 데이터의 개별적인 변동성에 더욱 민감할 수 있음을 의미합니다.
- 예를 들어, Traffic 데이터셋에서 Flashformer의 MAE 개선이 상대적으로 낮았는데, 이는 교통 데이터의 높은 불확실성과 변동성 때문일 수 있습니다.
결론적으로, 반전된 iTransformer 구조는 다양한 Transformer 변형에 걸쳐 일관된 성능 향상을 가져왔으며, 특히 복잡한 시간적 상관관계와 다변량 특성을 더 잘 모델링할 수 있도록 도움을 주었습니다. 이는 향후 Transformer 기반의 시계열 예측기 설계에 있어 매우 유망한 접근 방식임을 보여줍니다.
-----
변수 일반화(Variate Generalization)
기존 Transformer를 반전시킴으로써 모델들이 보지 못한 변수에 대한 일반화 능력을 가지게 된다는 점이 주목됩니다. 첫째로, 입력 토큰 수의 유연성 덕분에 변수 채널의 수가 더 이상 제한되지 않으며, 따라서 학습과 추론 시 변할 수 있게 되었습니다. 또한, iTransformer에서는 피드포워드 네트워크가 독립적인 변수 토큰에 동일하게 적용됩니다. 앞서 언급한 바와 같이, 필터 역할을 하는 뉴런들은 모든 시계열의 내재적 패턴을 학습하며, 이는 서로 다른 변수 간에 공유되고 이전될 수 있는 경향이 있습니다.
이 가설을 검증하기 위해, 우리는 다른 일반화 전략인 채널 독립성(Channel Independence)과의 비교를 수행했습니다. 이는 모든 변수를 예측하기 위해 공유된 백본을 훈련하는 방법입니다. 각 데이터셋의 변수를 다섯 개의 폴더로 나누고, 한 폴더의 변수 중 단 20%만을 사용하여 모델을 학습한 후, 모든 변수를 직접 예측하는 방식으로 실험을 진행했습니다. 성능 비교는 그림 5에 나와 있으며, 각 막대는 폴더의 랜덤성을 피하기 위해 모든 폴더의 평균 결과를 나타냅니다. CI-Transformers는 추론 중 각 변수를 하나씩 예측하는 데 많은 시간이 걸리는 반면, iTransformers는 모든 변수를 직접 예측하며 일반적으로 더 적은 성능 저하를 보였습니다. 이는 피드포워드 네트워크가 이전 가능한 시계열 표현을 학습하는 데 충분히 유능하다는 것을 의미합니다. 이로 인해 다양한 변수 수를 가진 다변량 시계열을 함께 학습할 수 있는 기반 모델을 iTransformer를 통해 구축하는 방향이 유망할 수 있습니다.
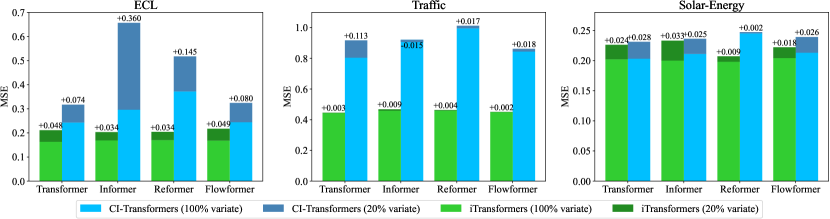
그림 5: 보지 못한 변수에 대한 일반화 성능
각 데이터셋의 변수를 다섯 개의 폴더로 나누고, 20% 변수로 모델을 학습한 뒤 부분적으로 학습된 모델을 사용해 모든 변수를 예측합니다. iTransformers는 효율적으로 학습할 수 있으며, 예측 시 좋은 일반화 능력을 보입니다.
과거 관찰 길이의 증가(Increasing Lookback Length)
이전 연구에서는 Transformer에서 과거 관찰 길이(lookback length)가 증가해도 예측 성능이 반드시 향상되지 않는 현상을 목격했습니다(Nie et al., 2023; Zeng et al., 2023). 이는 입력이 증가하면서 주의(attention)가 분산되기 때문일 수 있습니다. 반면, 선형 예측에서는 일반적으로 과거 정보가 커짐에 따라 예측 성능이 향상되는 경향이 있으며, 이는 통계적 방법(Box & Jenkins, 1968)에 의해 이론적으로도 뒷받침됩니다. 주의 메커니즘과 피드포워드 네트워크의 작동 차원이 반전됨에 따라, 우리는 그림 6에서 과거 관찰 길이가 증가함에 따른 Transformer와 iTransformer의 성능을 평가했습니다. 결과는 놀랍게도 MLP를 시간 차원에서 활용하는 것이 합리적임을 검증하였으며, 이를 통해 Transformer가 확장된 과거 창을 활용해 더 정밀한 예측을 할 수 있다는 것을 확인했습니다.

그림 6: 과거 관찰 길이 T∈{48,96,192,336,720}와 고정된 예측 길이 S=96에서의 예측 성능
Transformer 기반 예측기는 과거 관찰 길이 증가로 성능이 반드시 향상되지는 않지만, 반전된 프레임워크는 기존 Transformer와 그 변형 모델들이 확장된 과거 창에서도 향상된 성능을 보이도록 돕습니다.
4.3 모델 분석
제거 실험(Ablation Study)
Transformer 구성 요소의 합리성을 검증하기 위해, 구성 요소를 대체하거나(Replace), 제거하는(w/o) 실험을 포함한 상세한 제거 실험을 제공합니다. 결과는 표 3에 나와 있습니다. 변수 차원에서 주의(attention)를 사용하고 시간 차원에서 피드포워드 네트워크를 사용하는 iTransformer가 일반적으로 가장 좋은 성능을 달성했습니다. 특히, 기본 Transformer(세 번째 행)의 성능은 이 디자인들 중 가장 나쁜 성과를 보였으며, 이는 우리가 부록 E.3에서 자세히 설명한 기존 아키텍처의 잠재적인 위험성을 나타냅니다.
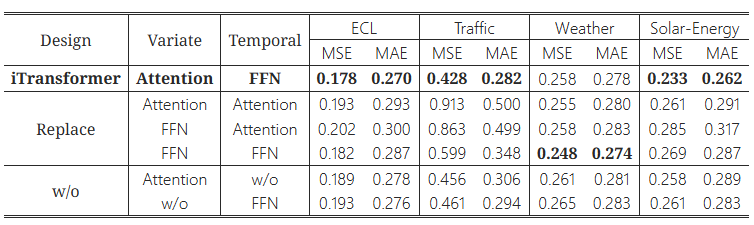
표 3: iTransformer의 제거 실험
우리는 다변량 상관관계(Variate)와 시계열 표현(Temporal)을 학습하기 위해 각각의 차원에서 다양한 구성 요소를 교체하는 실험과 구성 요소를 제거하는 실험을 수행했습니다. 모든 예측 길이에 대한 평균 결과가 여기에 나와 있습니다.
-----
이 표는 각각의 데이터셋 (ECL, Traffic, Weather, Solar-Energy)에 대해 MSE(평균 제곱 오차)와 MAE(평균 절대 오차)로 성능을 평가합니다. 각 행은 iTransformer에서의 다양한 설계 실험을 나타내며, 구성 요소를 교체하거나 제거했을 때의 성능 차이를 보여줍니다. 낮은 MSE와 MAE가 더 나은 성능을 의미합니다.
표의 주요 결과 해석
- iTransformer (Attention, FFN)
- 설계: 변수(Variate) 차원에서는 Attention을 사용하고, 시간(Temporal) 차원에서는 **Feed-Forward Network (FFN)**을 사용합니다.
- 성능: 모든 데이터셋에서 가장 낮은 MSE와 MAE를 기록하며, ECL (MSE: 0.178, MAE: 0.270), Traffic (MSE: 0.428, MAE: 0.282), Weather (MSE: 0.258, MAE: 0.278), **Solar-Energy (MSE: 0.233, MAE: 0.262)**에서 최고의 성능을 보였습니다.
- 분석: 이 결과는 변수 상관관계 학습을 위해 Attention을, 시계열 표현 학습을 위해 FFN을 사용하는 설계가 가장 효과적임을 보여줍니다. 이는 변수 간의 상호작용을 적절히 학습하고 시간적 패턴을 잘 추출할 수 있는 구조임을 나타냅니다.
- Attention, Attention (Replace)
- 설계: 변수와 시간 두 차원 모두에서 Attention을 사용합니다.
- 성능: Traffic 데이터셋에서 MSE가 0.913로 매우 높고, MAE가 0.500으로 성능이 가장 저조했습니다. 다른 데이터셋에서도 전반적으로 성능이 낮았습니다.
- 분석: 변수와 시간 차원 모두에서 Attention을 사용하는 경우, 특히 변동이 심한 시계열 데이터에서는 성능이 크게 떨어지는 것을 확인할 수 있습니다. 이는 Attention 메커니즘이 많은 정보를 동시에 다룰 때 집중력이 분산되어 예측 성능이 저하될 수 있음을 시사합니다.
- FFN, Attention (Replace)
- 설계: 변수 차원에서는 FFN을, 시간 차원에서는 Attention을 사용합니다.
- 성능: Traffic 데이터셋에서 성능이 좋지 않았으며(MSE: 0.863, MAE: 0.499), Solar-Energy 데이터셋에서도 MSE가 0.285로 높았습니다.
- 분석: 시간 차원에서 Attention을 사용하면 시계열의 시간적 종속성을 효과적으로 학습하기 어려울 수 있습니다. 이는 시간적 패턴을 FFN보다 적절히 학습하지 못해 예측 성능이 떨어진다는 것을 의미합니다.
- FFN, FFN (Replace)
- 설계: 변수와 시간 차원 모두에서 FFN을 사용합니다.
- 성능: ECL 데이터셋에서 MSE 0.182, MAE 0.287로 상당히 좋은 성능을 보였지만, Traffic 데이터셋에서는 MSE가 0.599로 성능이 떨어졌습니다.
- 분석: 두 차원 모두에서 FFN을 사용하면 어느 정도 성능은 보장되지만, Attention을 통해 변수 간의 복잡한 상호작용을 모델링하지 못해 다변량 데이터에서는 성능이 저하될 수 있습니다.
- w/o Attention (w/o Attention, w/o)
- 설계: Attention을 제거하고 피드포워드 네트워크만 사용합니다.
- 성능: 모든 데이터셋에서 iTransformer보다 성능이 떨어졌습니다. 예를 들어, Traffic 데이터셋에서 MSE가 0.456으로 높았습니다.
- 분석: Attention이 제거되면서 변수 간의 상호작용을 학습하지 못해 다변량 데이터셋에서 성능이 저하되었습니다. 이는 Attention 메커니즘이 다변량 간의 복잡한 관계를 잘 학습할 수 있음을 보여줍니다.
- w/o FFN (w/o FFN)
- 설계: FFN을 제거하고 Attention만 사용합니다.
- 성능: 모든 데이터셋에서 FFN이 포함된 설계보다 성능이 떨어졌습니다. 예를 들어, Weather 데이터셋에서 MSE가 0.265로 더 높았습니다.
- 분석: FFN이 제거된 경우, 시간적 패턴을 비선형적으로 학습할 수 있는 능력이 떨어져 성능이 저하됩니다. 이는 시간 차원에서 FFN의 역할이 매우 중요함을 의미합니다.
종합적인 분석
- 최고 성능 설계: Attention + FFN
- 변수 차원에서의 Attention과 시간 차원에서의 FFN을 사용하는 기본 iTransformer 설계가 모든 데이터셋에서 일관되게 가장 좋은 성능을 보였습니다. 이는 다변량 상관관계 학습과 시간적 패턴 학습의 균형을 잘 잡는 설계임을 시사합니다.
- 대체 및 제거 실험
- Attention을 두 차원 모두에 사용하는 경우와 FFN만 사용하는 경우는 다변량 간의 상호작용과 시간적 패턴을 동시에 잘 모델링하지 못해 성능이 저하되었습니다.
- Attention이나 FFN을 제거한 경우에도 전반적으로 성능이 떨어졌습니다. 이는 두 구성 요소가 서로 보완적으로 작용하여 복잡한 다변량 시계열 예측에서 중요한 역할을 한다는 점을 보여줍니다.
- 특히 Traffic 데이터셋에서의 성능
- Traffic 데이터셋은 다른 데이터셋보다 복잡한 변동을 가지고 있어, 모든 구성 요소가 조화를 이루어야만 높은 성능을 달성할 수 있습니다. 여기서 iTransformer의 성능이 돋보였으며, 이 구조가 변동성이 큰 데이터에서도 안정적으로 작동함을 알 수 있습니다.
결론적으로, 변수 차원에서의 Attention과 시간 차원에서의 FFN을 사용하는 iTransformer의 설계가 모든 실험에서 가장 좋은 성능을 보였으며, 이는 Transformer의 구성 요소들을 올바르게 사용하는 것이 시계열 예측 성능에 매우 중요하다는 점을 강력히 뒷받침합니다.
-----
시계열 표현 분석
피드포워드 네트워크가 시계열 표현을 추출하는 데 더 적합하다는 주장을 추가로 검증하기 위해, 중심 커널 정렬(CKA) 유사성(Kornblith et al., 2019)에 기반한 표현 분석을 수행했습니다. CKA 값이 높을수록 더 유사한 표현을 나타냅니다. Transformer 변형 모델들과 iTransformer에 대해, 우리는 첫 번째 블록과 마지막 블록의 출력 특징들 간의 CKA를 계산했습니다. 주목할 점은 이전 연구들이 시계열 예측은 저수준 생성 작업으로서 더 나은 성능을 위해 높은 CKA 유사성을 선호한다는 것을 보여주었습니다(Wu et al., 2023; Dong et al., 2023). 그림 7에 나타난 것처럼, 명확한 구분선이 존재하며, 이는 iTransformer가 차원을 반전하여 더 적절한 시계열 표현을 학습하였고 따라서 더 정확한 예측을 달성했음을 의미합니다. 이 결과는 또한 Transformer의 반전이 예측 백본의 근본적인 개혁이 될 가치가 있음을 지지합니다.
다변량 상관관계 분석
다변량 상관관계의 역할을 주의 메커니즘에 부여함으로써, 학습된 맵은 향상된 해석 가능성을 갖습니다. 우리는 그림 7에서 Solar-Energy 데이터의 시계열에 대한 사례 시각화를 제공하며, 과거 창과 미래 창에서 뚜렷한 상관관계를 보여줍니다. 얕은 주의 레이어에서는 학습된 맵이 원시 입력 시계열의 상관관계와 많은 유사성을 공유하는 것을 관찰할 수 있습니다. 깊은 레이어로 들어갈수록, 학습된 맵은 점차 미래 시계열의 상관관계와 유사해지며, 이는 반전된 작업이 상관 관계를 해석할 수 있는 주의 메커니즘을 강화하고, 과거를 인코딩하고 미래를 예측하는 과정이 피드포워딩 동안 시계열 표현에서 본질적으로 수행된다는 것을 검증합니다.

그림 7: 시계열 표현과 다변량 상관관계 분석
왼쪽: Transformer와 iTransformer 간의 시계열 표현의 MSE 및 CKA 유사성 비교. 더 높은 CKA 유사성은 더 정확한 예측을 위한 더 적합한 표현을 나타냅니다.
오른쪽: 반전된 자기 주의 메커니즘에 의해 학습된 점수 맵과 원시 시계열의 다변량 상관관계 사례 시각화.
효율적인 학습 전략
자기 주의의 이차 복잡성으로 인해, 많은 변수를 학습하는 것이 상당히 부담이 될 수 있으며, 이는 실제 시나리오에서 매우 흔합니다. 효율적인 주의 메커니즘 외에도, 우리는 이전에 입증된 변수 생성 능력을 활용하여 고차원 다변량 시계열에 대한 새로운 학습 전략을 제안합니다. 구체적으로, 각 배치에서 변수의 일부만을 무작위로 선택하고, 선택된 변수로만 모델을 학습합니다. 반전 덕분에 변수 채널의 수가 유연하기 때문에, 모델은 예측을 위해 모든 변수를 예측할 수 있습니다. 그림 8에 나타난 것처럼, 제안된 전략의 성능은 전체 변수 학습과 비교했을 때 여전히 유사하지만, 메모리 사용량은 크게 줄일 수 있습니다.
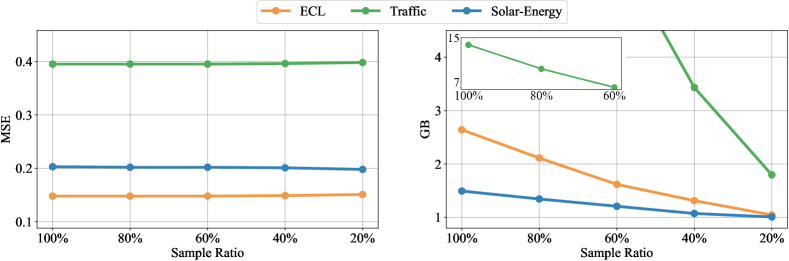
그림 8: 효율적인 학습 전략 분석
각 배치에서 부분적으로 학습된 변수에 대해 성능(왼쪽)은 다양한 샘플링 비율에서 안정적으로 유지되는 반면, 메모리 사용량(오른쪽)은 크게 줄일 수 있습니다. 종합적인 모델 효율성 분석은 부록 D에 제공합니다.
5. 결론 및 향후 작업
다변량 시계열의 특성을 고려하여, 우리는 기본 모듈을 수정하지 않고 Transformer의 구조를 반전시킨 iTransformer를 제안합니다. iTransformer는 독립된 시계열을 변수 토큰으로 간주하여 주의 메커니즘을 통해 다변량 상관관계를 포착하고, 층 정규화와 피드포워드 네트워크를 활용하여 시계열 표현을 학습합니다. 실험적으로, iTransformer는 최첨단 성능을 달성하였고, 유망한 분석에 의해 뒷받침되는 뛰어난 프레임워크 일반성을 보였습니다. 향후에는 대규모 사전 학습과 더 많은 시계열 분석 작업을 탐구할 계획입니다.
'인공지능' 카테고리의 다른 글
| [모델까지만]Moshi: a speech-text foundation model for real-time dialogue (1) | 2024.11.26 |
|---|---|
| LLaMA-Omni: Seamless Speech Interaction with Large Language Models (2) | 2024.11.26 |
| Pixtral 12B (1) | 2024.11.23 |
| DeepSeek-V2.5 (1) | 2024.11.23 |
| De novo design of high-affinity protein binders with AlphaProteo (3) | 2024.11.22 |


