Traveling Waves Integrate Spatial Information Through Time

https://arxiv.org/abs/2502.06034?utm_source=pytorchkr&ref=pytorchkr

Traveling waves of neural activity are widely observed in the brain, but their precise computational function remains unclear. One prominent hypothesis is that they enable the transfer and integration of spatial information across neural populations. Howev

arxiv.org

초록
뇌에서는 신경 활동의 진행파(traveling wave)가 널리 관찰되지만, 그 정확한 계산적 기능은 아직 명확히 밝혀지지 않았다. 한 가지 유력한 가설은 이러한 진행파가 신경 집단 간의 공간 정보를 전달하고 통합하는 데 기여한다는 것이다. 그러나 이러한 통합 처리에 진행파가 어떻게 활용될 수 있는지를 탐구한 계산 모델은 드물다. 우리는 "드럼의 모양을 들을 수 있는가?"라는 유명한 문제에서 영감을 받아—파동 역학의 정상모드(normal modes)가 기하 정보를 어떻게 인코딩하는지를 조명하는 문제—유사한 원리가 인공 신경망에서 활용될 수 있는지를 조사한다.

구체적으로, 우리는 시각 자극에 반응하여 은닉 상태에서 진행파를 생성하도록 학습하는 합성곱 순환 신경망(convolutional recurrent neural networks)을 제안하며, 이를 통해 공간 통합(spatial integration)을 가능하게 한다. 이후 이러한 파형(wave-like)의 활성화 시퀀스를 시각 표현(visual representations) 그 자체로 간주함으로써, 전역적 공간 맥락이 필요한 작업에서 지역 피드포워드 네트워크(local feed-forward networks)를 능가하는 강력한 표현 공간을 얻게 된다. 특히, 진행파는 지역 연결 뉴런(locally connected neurons)의 수용장을 효과적으로 확장시켜, 장거리 인코딩 및 정보 전달을 지원하는 것으로 나타났다.

우리는 이 메커니즘을 갖춘 모델이 전역 통합(global integration)이 요구되는 시각 의미 분할(semantic segmentation) 작업을 성공적으로 해결하며, 지역 피드포워드 모델보다 뛰어난 성능을 보이고, 더 적은 파라미터로 비지역적(non-local) U-Net 모델과 견줄 만한 성능을 달성함을 보여준다. 이는 인공 신경망에서 진행파 기반의 통신 및 시각 표현을 향한 첫걸음으로, 우리의 연구는 파동 역학(wave dynamics)이 효율성과 학습 안정성 측면에서 이점을 제공할 뿐 아니라, 생물학적 신경 활동 기록과 인공 모델을 연결하는 새로운 틀을 제시할 수 있음을 시사한다.

키워드: 진행파(Traveling Waves); 진동(Oscillation); 정보 통합(Information Integration)

서론

신경 활동의 진행파(traveling wave) 전파는 가장 초기의 신경 기록(Adrian & Matthews, 1934; Goldman 외, 1949; Lilly, 1949; Mickle & Ades, 1953)에서도 대뇌 표면에서 측정된 바 있다. 이러한 파동은 피질 영역을 국지적(local)으로 또는 전역적(globally)으로 다양한 속도로 이동하는 것으로 측정되었다(Reimer 외, 2010; Muller 외, 2016; Zhang 외, 2018). 자극에 의해 유발된 진행파는 시각 피질에서 직접 측정되었으며(Cowey, 1964), 이후 침습 전극(Ebersole & Kaplan, 1981)부터 전압 민감 염색(vsd) 영상(Muller 외, 2014), 그리고 깨어 있는 영장류의 행동 실험(Davis 외, 2020)까지 점점 더 정교한 방법론으로 연구되었다.

이러한 관찰 결과를 바탕으로, 이 동역학(dynamics)의 기능적 역할을 설명하기 위한 다양한 이론들이 제안되어 왔다. 예를 들어, 진행파는 예측 부호화(predictive coding)(Alamia & VanRullen, 2019), 대칭성 표현(symmetry representation)(Keller 외, 2024), 장기 기억의 고착화(consolidation)(Muller 외, 2018), 운동 정보의 인코딩(Heitmann & Ermentrout, 2020)과 관련된 것으로 제안되어 왔다.

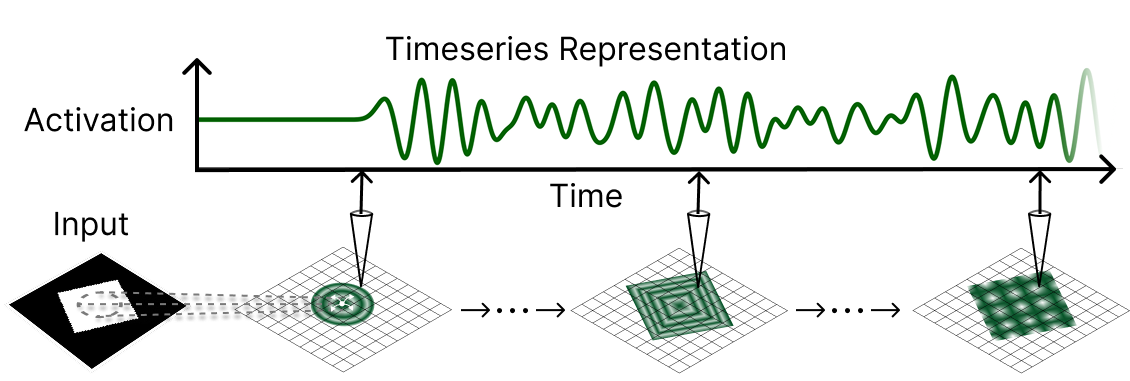
그림 1 설명
시각 자극은 뉴런 격자(lattice)의 초기 조건을 설정하고, 각 뉴런의 국지적 수용장(local receptive field) 및 순환 연결(recurrent connectivity)에 기반한 반응 특성을 정의한다. 이 초기 조건은 순환 파동 동역학(recurrent wave dynamics)에 따라 시간이 지남에 따라 진화하며, 각 뉴런에서 생성된 시계열(timeseries)은 시각 자극에 대한 전역적으로 통합된 표현(global integrated representation)이 된다.

본 연구와 가장 관련 깊은 가설 중 하나는, 진행파가 장거리 정보 통합 및 전달을 위한 메커니즘 역할을 한다는 것이다. 특히, 이러한 메커니즘은 시각 피질 내에서 중요한 역할을 수행하는 것으로 여겨진다(Sato 외, 2012). 예를 들어, Kitano 외(1994)는 시각 자극이 고전적인 망막 위치 수용장(retinotopic receptive field) 바깥에 있을 때도 1차 시각 피질의 뉴런에서 국소장 전위(LFP) 반응이 유도될 수 있으며, 반응 지연(latency)은 거리와 비례한다는 점을 보여주었다. 이는 장거리 거리 지연 통합(long-range distance-delayed integration)을 시사한다. 이러한 발견은 이후 Bringuier 외(1999)의 세포내 막전위 기록을 통해 강화되었으며, 이들은 확장된 수용장을 "시각 유도 시냅스 통합 필드(visually evoked synaptic integration field)"라 명명하였다.

그러나 정보 통합과 전달이라는 가설적 역할은 시각 자극을 넘어서 확장된다. 예를 들어, Rubino 외(2007)는 운동 준비 중인 원숭이의 운동 피질에서 베타 주파수 진동(beta-frequency oscillations)이 공간적으로 전파되며, 이러한 파동이 시각 목표물의 정보를 직접 인코딩한다고 보고했다. 또한 Besserve 외(2015)는 방향 특이적인 인과 정보 전달 지표를 통해 감마 주파수 대역의 진행파가 서로 다른 피질 영역 간의 정보 전달과 상관되어 있음을 보여주었으며, Bhattacharya 외(2022)는 작업 기억 과제 중 정보 검색과 처리 과정에서 진행파의 방향이 바뀐다는 사실을 밝혀냈다.

하지만 이러한 유망한 관찰 결과에도 불구하고, 진행파 동역학을 보이는 과제 학습 가능(task-trainable)한 인공 신경망 모델이 부족하기 때문에, 이를 계산적으로 탐구하는 일은 여전히 도전적이다. 현대 인공 신경망에서는 입력(예: 이미지)의 공간적인 거리 또는 시퀀스의 ‘토큰’ 간 정보를 통합하거나 전달하기 위해 매우 깊은 합성곱 신경망(He 외, 2015), 병목/풀링 계층(Ronneberger 외, 2015), 또는 트랜스포머에서처럼 전체 연결 구조(all-to-all connectivity)(Vaswani 외, 2023)를 사용한다. 이러한 접근 방식은 각기 고유한 계산 복잡도와 표현력 한계를 가지므로, 신경계에서 분산된 정보를 통합하는 대안적 방법을 탐색하는 것은 큰 의미가 있다.

이 논문에서 우리는 파동 기반 모델의 계산적 잠재력을 탐색하고, 정보 전달에서의 파동 동역학의 인과적 역할을 이해하기 위한 첫걸음을 내딛는다. 이를 위해 우리는 “드럼의 모양을 들을 수 있는가?”라는 수학적 질문에서 영감을 받아, 이 문제의 핵심 기법인 파동 기반 동적 시스템(wave-based dynamical systems)의 정상해(stationary solutions)를 통해 전역 정보를 표현하는 방식이 시간에 따라 변화하는 순환 신경망 은닉 상태에서도 전역 정보를 추출하는 데 동일하게 적용될 수 있는지를 탐구한다.

논문의 첫 번째 부분에서는 이 문제와 관련된 형식적 이론을 검토하고, 이 아이디어를 계산 원리로 활용할 수 있는 학습 가능한 순환 신경망을 어떻게 구성할 수 있는지를 개괄한다. 단순 과제에서 우리는 이러한 간단한 모델이 실제로 이론적 예측과 일치하며(Figure 2), 주파수 공간에서 단순한 형태들을 구분(disentangle)하는 파동 동역학을 생성할 수 있음을 보여준다(Figures 3 & 4).

논문의 두 번째 부분에서는 이 직관을 바탕으로, 초기 인코더와 순환 연결이 모두 국지적 수용장 제약을 가진 합성곱 순환 신경망(conv-RNN)을 구축하고, 이를 보다 복잡한 전역 정보 처리 과제(의미 분할 등)에 적용해본다. 우리는 각 뉴런의 순환 활성화 시계열을 학습 중 주요 표현(primary representation)으로 사용하여(Figure 1 도식 참조), 이 모델이 지역적으로 제약된 다른 모델보다 우수한 성능을 내고, 일부 깊은 합성곱 모델(U-Net 등)과도 경쟁할 수 있으며, 학습이 더 안정적으로 수렴함을 보여준다. 결국 이는 진행파 기반 정보 통합이 기존 딥러닝 기반 공간 통합 기술에 대한 효율적이고 안정적인 대안이 될 수 있음을 시사한다.

동기: 드럼의 모양을 들을 수 있을까?

진행파(traveling wave)가 공간 상의 정보를 어떻게 통합할 수 있는지에 대한 직관을 얻기 위해, 우리는 Mark Kac(1966)이 제기한 유명한 수학적 질문 “드럼의 모양을 들을 수 있는가?”에서 영감을 얻는다. 간단히 말해, 이 질문은 이상화된 드럼 헤드(진동막)가 진동하는 고유 진동수들로부터 그 경계 조건(boundary condition)을 고유하게 식별할 수 있는지를 묻는다.

직관적으로 설명하자면, 드럼 헤드를 한 번 두드리면 초기 자극이 일시적인 진행파로 바깥쪽으로 퍼져나가며, 고정된 경계 조건에 도달하면 위상 이동과 함께 반사된다. 이 반사파는 경계에 대한 정보를 수집한 뒤 중심을 향해 돌아오게 된다. 이러한 파동들은 결국 모양의 모든 가장자리에서 반사된 파동들과 충돌하고, 다양한 파면(wavefront)이 중첩되어(superposition) 파형이 형성된다. 궁극적으로, 이는 경계 조건에 의해 제한된 이산적인 정상 모드(normal modes)의 중첩으로 표현되는 해(solution)로 수렴하게 된다.

높은 수준에서 볼 때, Kac의 질문은 공간적으로 국지적인 파동 방정식(wave equation)이 전역적인 조건(고정된 드럼 경계)에 의해 결정되는 정상 상태 해로 진화함으로써, 어떻게 전역 정보를 통합할 수 있는지를 보여주는 메커니즘 하나를 탐구한다. 물론 뇌줄기에서 발견되는 부울부엉이(owl)의 지연선(delay-line) 메커니즘(Jeffress, 1948; Carr & Konishi, 1988)이나, 파면 간섭(interfering wave fronts)과 같은 복잡한 메커니즘(Gong & Van Leeuwen, 2009; Izhikevich & Hoppensteadt, 2009) 등, 정보 전달 및 통합을 설명할 수 있는 다른 메커니즘들도 존재한다. 하지만 이 정상 상태 해 기반의 메커니즘은 계산 모델을 구축하기 위한 출발점으로서 강력하며 잘 이해된 접근이다.

형식적으로 이 문제에서의 "드럼"은 완전히 탄성적인 2차원 막(membrane)으로 간주되며, 공간과 시간에 따른 수직 변위(vertical displacement)는
u(x, y, t)
로 나타낸다. 이 드럼 헤드는 일정한 장력 하에 모양이 Ω인 경계(boundary)로 팽팽하게 고정되어 있으며, 그 동역학은 파동 속도 c가 일정한 2차원 파동 방정식(two-dimensional wave equation)을 만족한다.

원래 문제에서는, 드럼 헤드가 경계에서 변위가 0이 되도록 고정(clamped)되어 있으며, 이는 Dirichlet 경계 조건(Dirichlet boundary condition)으로 알려져 있다. 이러한 조건은 보통 다음과 같이 표현된다:
u |_∂Ω= 0.
우리는 정상 상태의 진동 해(steady-state oscillatory solutions)에 관심이 있으므로, 해는 반드시 특정 진동수 ω_k를 갖는 고유 진동 모드(normal mode)
ϕ_k(x, y)
의 형태를 가져야 한다고 볼 수 있다.

이를 식 (1)에 대입하면, 해는 다음 조건을 만족해야 함을 알 수 있다:

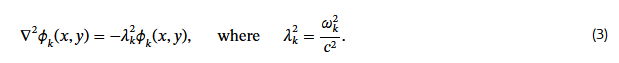
이 형태로 보면, λ_k는 표면 u에 작용하는 라플라시안(Laplacian) 연산자의 고유값(eigenvalue)임이 명확하다. 요약하자면, Kac(1966)이 제기한 질문은 다음과 같다: 주어진 경계 조건 위에서 라플라시안이 갖는 전체 고유값 집합 {λ₁, λ₂, …} (이를 고유스펙트럼, eigenspectrum이라 함)가 모든 2차원 경계(boundary)를 고유하게 식별하기에 충분한가?

이 질문이 처음 제기되었을 당시, 드럼 헤드의 면적은 그 고유스펙트럼으로부터 유일하게 추론할 수 있음이 알려져 있었다. 그러나 이후 고유스펙트럼이 동일하지만 서로 다른 모양을 가진 드럼 헤드들이 존재한다는 반례(counterexample)가 발견되기까지는 25년 이상이 걸렸다(Gordon 외, 1992). 이후 Zelditch(1999)의 연구에서는 고유하게 식별 가능한 형상의 클래스를 정밀하게 특성화할 수 있었다.

종합적으로 볼 때, 이러한 결과들은 스펙트럼 표현(spectral representation)에 담긴 고유한 기하학적 정보가 상당히 풍부하며, 일부 병적인(pathological) 예외를 제외하면 대부분의 형상은 ‘등스펙트럼(isospectral)’이 아니다, 즉 서로 다른 고유스펙트럼을 가진다는 점을 보여준다.

정사각형 드럼에 대한 해

변의 길이가 L인 정사각형 드럼의 경우, 위에서 설명한 경계값 문제(boundary value problem)는 잘 알려진 단순한 해를 갖는다(Bérard & Helffer, 2014).
구체적으로, 이 경우의 정상 모드(normal modes)와 해당하는 라플라시안 고유값(Laplacian eigenvalues)는 다음과 같다:

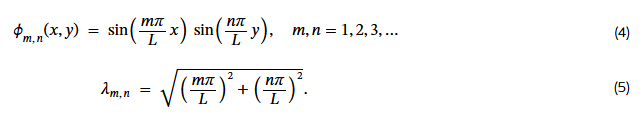
이러한 모드들이 정사각형 경계에서 정확히 0이 됨을 우리는 쉽게 확인할 수 있다.
예를 들어,
sin(n·π·x / L) = sin(0) = 0 일 때 x = 0,
sin(n·π·x / L) = sin(n·π) = 0 일 때 x = L이기 때문이다.

식 (3)에 따라, 파동 방정식에서의 진동수(oscillation frequencies)는 다음과 같다:

ω_m,n = c · λ_m,n = c · (π / L) · √(m² + n²)

따라서, 정사각형 드럼의 가장 낮은 공진 주파수(lowest resonant frequency)는 다음과 같다:

(진동수는) 초당 라디안 단위(radians per second)로 측정되며, 이는 드럼의 크기 L이 클수록 더 낮은 음정(더 작은 ω_1,1)을 낸다는 우리의 직관과 일치한다.

우리가 제안하는 핵심 아이디어—이러한 전역 정보 통합 메커니즘이 순환 신경망(recurrent neural network, RNN) 내에서 합리적으로 시뮬레이션될 수 있는지—를 검증하기 위해, 다음 단계에서는 파동 동역학(wave dynamics)을 모방하는 간단한 RNN 모델을 구현하고, 그 은닉 상태의 동역학으로부터 얻어진 푸리에 변환(Fourier transform)이 실제로 이러한 기본 진동수(fundamental frequencies*를 나타내는지를 측정한다.

순환 신경망에서의 모사 (Emulation in a Recurrent Neural Network)

위의 파동 방정식(식 1)을 RNN에서 시뮬레이션하기 위해, 우리는 파동 방정식이 시공간상에서 이산화(discretization)될 수 있으며, 이때 유도되는 일련의 방정식들이 RNN 구조와 매우 유사하다는 점에 주목한다.
이는 Keller 외(2024)가 1차 편향 파동 방정식(one-way wave equation)에 대해 사용한 접근 방식이며, Rusch & Mishra(2021)가 상호 연결된 진동 네트워크(coupled oscillations)에 대해 적용했던 방식과 유사하나, 여기서는 이를 표준적인 2차원 파동 방정식에 맞게 조정하였다.

구체적으로, 우리는 Verlet 적분(Verlet integration)을 사용하여 파동 방정식을 정확하게 수치적으로 적분하는 RNN 구조를 구성하며, 이에 따라 은닉 상태 𝐡와 연관된 속도 상태 𝐯(coupled velocity state)에 대해 다음과 같은 업데이트 식을 얻게 된다:

여기서
𝐡 ∈ ℝ_H×W 는 두 개의 공간 차원(H, W)을 가지는 은닉 상태로 정의되며,
⋆ 는 이 공간 차원에 대한 합성곱(convolution)을 의미한다.
또한 K_∇² 는 2차원에서 이산 라플라시안 연산자(discrete Laplacian operator)를 표현하는 5점 스텐실(five-point stencil)을 나타낸다:

RNN에 ‘드럼을 입력으로 제공’하는 가장 직관적인 방법은, 드럼을 이산화된 격자(discretized grid) 위에 존재하는 것으로 간주하고 (이미지처럼), 각 공간 위치 (x, y)를 해당하는 뉴런 h_x,y에 매핑하는 것이다.

그런 다음, 학습된 이상적 인코더를 모방하기 위해 정사각형의 경계 및 그 외부에 있는 뉴런들의 값을 0으로 고정(clamp)한다. 명시적으로는 다음과 같다:
h_x,y = 0 ∀ {x, y} ∈ ∂Ω.

이후 초기 조건(initial condition)을 설정할 수 있는데, 드럼 중앙의 은닉 상태 h_cₓ,cᵧ를 1로 설정하고, 그 외의 모든 위치는 0으로 설정한 뒤, 앞서 정의한 동역학을 시간에 따라 전개(unfold)하도록 하면 된다.

그림 2: Wave-RNN은 이론적인 주파수를 생성한다.

변의 길이 L이 다른 정사각형 드럼 헤드에 대해, 이론적으로 예측된 기본 주파수(Hz 단위, cycles/sec)와, 정사각형 입력을 기반으로 순환 동역학을 결정하는 파동 기반 RNN(wave-based RNN)에서 측정된 가장 낮은 피크 주파수를 비교한 결과를 나타낸다.

그림 2에서는 이 실험의 결과를 제시한다.

x축에는 정사각형의 변 길이 L을 13에서 21까지 변화시키며, 각 L에 대해 이론적인 기본 주파수(Hz)를 ω_1,1 = c·2 / (2·L)
로 계산한다. 그에 대응하는 가장 낮은 피크 주파수는, 은닉 상태 h_cₓ,cᵧ의 동역학을 40,000 타임스텝 동안 (Δt = 0.025) 시뮬레이션한 후 푸리에 변환(Fourier transform)을 통해 측정하며, 이 값을 y축에 나타낸다. 결과적으로, 파동 기반 RNN의 출력은 이론적 예측과 거의 완벽하게 일치하며, 작은 오차는 수치적 적분(numerical integration)의 한계에 기인한 것으로 보인다.

그림 3: 파동은 도형의 내부와 외부에서 다르게 전파되며, 전역적인 형태 정보를 내부로 통합한다.

다각형 이미지에서 변의 개수에 따라 픽셀을 분류하도록 학습된 국지 인코더(local encoder)와 순환 연결(recurrent connection)만을 사용하는 진동자 모델(oscillator model, NWM)의 은닉 상태 시퀀스를 보여준다. 모델은 도형의 내부와 외부에 서로 다른 고유 진동수(natural frequency)를 사용함으로써 부드러운 경계(soft boundary)를 형성하고, 이를 통해 파동 반사(reflection)를 유도하여, 도형의 형태에 따라 상이한 내부 동역학을 생성하는 법을 학습한 것을 볼 수 있다.

실험: 시맨틱 분할 (Semantic Segmentation)

이제 앞서 이론적 동기에서 얻은 직관을 바탕으로, 진행파(traveling wave)가 전역 정보 통합(global information integration)이 필요한 작업을 해결하기 위해 국지적으로 제약된 순환 신경망 구조에서 사용될 수 있는지를 실험적으로 살펴본다.

모든 실험에서의 과제는 시맨틱 분할(semantic segmentation)이며, 이는 원본 이미지의 각 픽셀을 배경(background) 또는 데이터셋 내 클래스 중 하나로 분류하는 작업이다. 모델은 픽셀 단위의 교차 엔트로피 손실(pixel-wise cross-entropy loss)을 최소화하도록 학습된다.

핵심적으로, 모든 국지적 제약(locally restricted) 모델은

3×3 커널을 사용하는 얕은(shallow) 합성곱 인코더,
합성곱 순환 연결(convolutional recurrent connections),
그리고 픽셀 단위 디코더(pixel-local decoders)를 사용한다.

이로써, 각 뉴런의 피드포워드 경로 내 수용장(spatial receptive field)은 단일 전파만으로는 클래스 레이블 판별에 필요한 특징의 전역 크기(inherent length scale)보다 훨씬 작게 제한된다.
즉, 모델이 과제를 성공적으로 수행한다면, 그것은 반드시 순환 연결을 통해 전역 정보를 통합한 결과임을 의미한다.

비교 기준으로는, 2층부터 32층까지 다양한 깊이의 CNN 모델을 사용하며, 이들은 이미지 상에서 국지(local)에서 전역(global)에 이르는 다양한 수용장을 갖는다.
또한, 마지막의 보다 복잡한 데이터셋들에 대해서는, 전역 정보 전달을 위해 깊이(depth)와 공간 병목(spatial bottleneck)을 동시에 사용하는 고급 U-Net 구조(Ronneberger 외, 2015)와도 비교를 수행한다.

전체 학습 세부사항은 보충 자료(supplementary material)를 참고하고,
논문 결과에 대한 전체 코드 및 영상 시각화는 아래에서 확인할 수 있다:
https://github.com/anonymous123-user/Traveling_Waves_Integrate

데이터셋 (Datasets)

진행파(traveling waves)를 이용해 넓은 공간적 거리(spatial distance)를 따라 정보를 전달할 수 있는지, 그리고 이러한 전역 정보를 과제에 맞게 해석(decode)할 수 있는지를 검증하기 위해, 다음의 네 가지 주요 데이터셋을 사용한다:

1. Polygons

가장 먼저, 흰색 다각형이 검정 배경 위에 그려진 단순한 합성 데이터셋을 사용한다.
여기서 클래스는 다각형의 변(edge) 개수로 정의된다.

입력: 1~2개의 다각형이 있는 75×75 픽셀의 회색조 이미지
각 도형: 변의 수가 3-6개이며, 반지름 15-20픽셀의 원 안에 근사적으로 내접
특징: 각의 개수(즉, 코너의 각도 정보)가 해당 클래스 식별에 충분하지만,
→ 이를 내부 영역까지 전달해야 도형 내부 픽셀을 정확히 분할할 수 있다
→ 정보의 전파가 필요한 구조

2. Tetrominoes

조금 더 복잡한 구조로, 이전 시맨틱 분할 연구(Miyato 외, 2024)에서 사용된 Tetrominoes 데이터셋을 다시 구현하여 사용한다 (Kabra 외, 2019).
이는 테트리스 조각과 유사한 다양한 형태와 색상의 블록들로 구성된 이미지이다.

입력: 1~5개의 블록이 있는 이미지 (검정 배경 위에 무작위 배치)
총 6개의 고유한 블록 클래스, 크기: 14~28픽셀
특징: Polygons보다
→ 형태 다양성,
→ 블록 수 증가
→ → 분할 과제가 더 어려움

3. MNIST

기본적인 MNIST 데이터셋(LeCun, 1998)을 사용하되,
이미지 해상도를 56×56으로 업샘플링(interpolation)한다.

처리: 픽셀 값을 0.5 기준으로 이진화(binarization)
라벨: 해당 숫자의 클래스 레이블 또는 배경
특징: 앞선 두 과제보다 훨씬 어려움
→ 같은 숫자라도 필기체 형태가 다름
→ 모델은 동역학 표현(dynamic representation) 안에서 불변성(invariance)을 학습해야 함

4. Multi-MNIST

마지막으로, 기존 Multi-MNIST 데이터셋(Sabour 외, 2017)을 변형하여 사용한다.

입력: 하나의 이미지에 1~4개의 숫자가 무작위로, 겹치지 않게 배치됨 (128×128 해상도)
생성 방식:
- 각 숫자(MNIST, 28×28)를 42×42로 업샘플링
- 이를 큰 캔버스에 무작위로 배치
처리: 0.5 기준 이진화, 각 픽셀은 해당 숫자 클래스 또는 배경으로 라벨링
특징:
- 이미지 크기 증가 → 공간 통합 거리 증가
- 숫자 개수/위치의 조합적 다양성 증가
  → 따라서 전 과제들보다 훨씬 어려운 분할 문제

이러한 데이터셋들은 난이도에 따라 구성되며, 진행파 기반 모델이 전역 정보를 어떻게 학습하고 활용하는지를 단계적으로 검증하기 위해 설계되어 있습니다.

그림 4: 파동 기반 모델은 주파수 공간에서 서로 다른 형태를 분리하는 법을 학습한다.

(왼쪽): 특정 테스트 이미지에 대해, 예측된 시맨틱 분할 결과와 각 픽셀에 대한 선택된 일부 주파수 구간(frequency bin)을 시각화한 그래프
(오른쪽): 데이터셋 내 각 도형 클래스에 대해, 해당 클래스 라벨을 가지는 모든 픽셀의 주파수 스펙트럼을 평균한 결과

이 그래프들을 통해 우리는 서로 다른 도형들이 서로 질적으로 다른 주파수 스펙트럼(frequency spectrum)을 갖는다는 것을 확인할 수 있으며,
이를 바탕으로 테스트 세트에서 픽셀 단위 분류 정확도 99% 이상을 달성할 수 있었다.

모델 구조 (Models)

이 절에서는 본 연구에서 사용한 국지 순환 모델(local recurrent models)과 전역 처리 기반 기준 모델(global baselines)에 대해 설명한다. 모든 모델에서 입력 이미지는 𝐱 ∈ ℝ_C×H×W 형태이고, 목표 출력은 𝐲 ∈ ℝ_N×H×W, 즉 각 픽셀에 대해 N개의 클래스 로짓(logit)을 예측하는 구조이다.

Locally Coupled Oscillatory RNN (NWM)

앞서 소개한 드럼 비유(drum analogy)를 가장 밀접하게 따르는 모델로서, 우리는 국지적으로 연결된 진동자(locally coupled oscillators) 네트워크 형태로 파라미터화된 순환 신경망(RNN)을 구현한다. 이 모델은 이전 연구들에서 Neural Wave Machine (NWM)이라 불렸으며 (Keller & Welling, 2023), coRNN 구조(Rusch & Mishra, 2021)를 기반으로 하고 있고, 진행파 동역학(traveling wave dynamics)을 자연스럽게 유도하는 경향이 있는 것으로 알려져 있다. 실제로 뉴런 수가 매우 많아지는 연속계 극한(continuum limit)에서는, 이러한 결합 진동자 네트워크(coupled oscillator networks)는 식 (1)에 해당하는 파동 방정식(wave dynamics)으로 정확히 수렴하는 것으로 알려져 있다(Schwartz, 2016). 구체적으로, 이 모델의 동역학은 다음과 같다:

여기서 σ = tanh는 쌍곡 탄젠트 함수(hyperbolic tangent function)이다. 본 연구에서는 이론 섹션에서처럼 은닉 상태를 명시적으로 고정(clamp)하지 않고도 순환 동역학이 입력에 따라 달라지도록 만들기 위해, 기존 NWM 구조를 다음과 같이 수정한다:

각 진동자의 자연 진동수 γ와 감쇠 항 α를 입력 이미지의 함수로 정의하며, 이 값들은 얕은 3층 CNN 모델을 통해 계산된다
→ γ_θ(𝐱), α_θ(𝐱)

이러한 설계는 은닉 상태 상에서의 파동 전파 방식(즉, 시간에 따른 동역학)을 입력 이미지가 직접 결정하도록 해주며, 특히 자연 진동수의 큰 차이를 통해 부드러운 경계 조건(soft boundary conditions)을 모사할 수 있게 해준다 (이는 Figure 3에서 확인 가능).

또한 모델의 초기 은닉 상태는 얕은 4층 CNN 인코더 f_θ(𝐱)를 통해 설정되며, 3×3 커널을 사용한다. 중요하게도, 이 인코더의 최종 레이어에서의 수용장 크기(receptive field)는 9×9로 제한되어 있으며, 이는 앞서 언급된 모든 데이터셋의 도형 크기보다 현저히 작다.

→ 따라서 네트워크가 과제를 잘 수행하려면 반드시 순환 동역학을 통해 전역 정보를 통합해야 한다.

우리는 모델이 진행파 전파(wave propagation)에 편향되도록 유도하기 위해, 순환 합성곱 커널 𝐰ₕ를 식 (10)의 라플라시안 연산자(Laplacian operator)에 대한 유한차 근사(finite difference approximation)로 초기화한다. 또한, 부드러운 경계 조건(soft boundaries)을 유도하기 위해, 자연 진동수 인코더 γ_θ(𝐱)는 항등 함수(identity)로 초기화한다. 마지막으로 위에서 정의한 2차 미분 방정식(ODE)은 Rusch & Mishra (2021)의 Implicit-Explicit 통합 방식을 사용해 타임스텝 크기 0.1로 수치적으로 적분하며, 총 100 타임스텝 동안 시뮬레이션한다. 이 논문에서 사용된 모든 순환 합성곱은 경계 효과를 방지하기 위해 원형 패딩(circular padding)을 적용하였다.

MNIST 및 Tetrominoes 실험에서는 은닉 상태에 2채널을,
Multi-MNIST 실험에서는 16채널을 사용하였다.

컨볼루셔널 LSTM (Convolutional LSTM)

진행파 동역학(wave-dynamics)에 사전 편향을 두지 않고도, 다른 국지적 제약을 가진 순환 구조(locally-constrained recurrent architectures)가 어떻게 이 과제를 해결할 수 있는지를 탐구하기 위해, 우리는 전통적인 LSTM(Hochreiter & Schmidhuber, 1997)을 공간 차원에 대해 지역 합성곱(local convolution)으로 확장한 컨볼루셔널 LSTM을 구현한다. 즉, 원래의 밀집 연결(dense connections)을 모두 합성곱으로 대체한 구조이며, 구체적으로 다음과 같은 계산 과정을 따른다:

여기서

σ는 시그모이드(sigmoid) 활성화 함수
⊙는 요소별 곱(Hadamard product)
⋆는 공간 차원에 대한 합성곱(convolution)

🔧 구성 및 학습 조건

이 모델은 특별한 초기화 없이도 학습되며,
Figure 5에서 보여주듯이, 은닉 상태 내에서 파동 형태의 동역학을 자발적으로 형성하며
→ 공간 정보를 통합하고
→ 과제를 해결하는 법을 스스로 학습한다.
은닉 상태 채널 수는 2개로, 다른 모델들과 동일하게 맞췄다.
모든 LSTM은 20 타임스텝으로 학습되었는데,
이는 소규모 데이터셋에서 가장 성능이 좋게 나타난 설정이었다.
더 복잡한 설정에서는 100 스텝이 유리할 수 있지만,
→ 학습 시간이 지나치게 길어지기 때문에
→ 대규모 실험에서는 기본적으로 NWM 모델을 사용한다.

순환 읽기(예측) 방식 (Recurrent Readout)

위에서 설명한 두 개의 순환 모델(NWM과 ConvLSTM)에 대해, 은닉 상태 시퀀스로부터 클래스 레이블을 어떻게 추론(readout)할지를 결정해야 한다.가장 단순한 방법은, 마지막 타임스텝의 은닉 상태를 픽셀 단위 분류를 위한 ‘readout’ 네트워크에 입력하는 것이다. 이 방식을 사용한 모델은 Table 1에서 “Last”로 표기된다.

대안으로는, 더 긴 시간 구간의 은닉 상태 시퀀스에 대해 어떤 함수를 적용한 뒤 그 결과를 readout 네트워크에 입력하는 방법이 있다. 이때 사용할 수 있는 시간 프로젝션(time-projection) 함수에는 다음과 같은 방식들이 있다:

Max: 타임스텝별 은닉 상태의 최댓값을 취함
Mean: 평균값을 취함
FFT: 은닉 상태 시계열의 푸리에 계수 크기(Fourier coefficient amplitudes)를 계산
Linear: 전체 시계열에 대해 학습 가능한 선형 투영(learnable linear projection)을 적용

모든 경우에 대해, readout 모듈은 다음과 같이 구성된다:

Polygons, MNIST, Tetrominoes: 4층 MLP
Multi-MNIST: 6층 MLP

즉, 시간 정보를 어떻게 요약하느냐에 따라 예측 성능에 영향을 줄 수 있으며, 이를 다양한 방식으로 실험해 본 것이다.

피드포워드 CNN 기준 모델 (Feed-Forward CNN Baselines)

CNN 기준 모델(baseline)은 총 L개의 합성곱 계층으로 구성되며, 각 계층은 3×3 커널과 16개의 채널을 갖는다. 이 기준 모델은 다음 두 가지 목적을 가진다:

작은 L일 때:
→ 제한된 수용장(local receptive field)만을 갖는 뉴런들이
→ 전역 정보가 필요한 작업을 수행할 수 없음을 보여주는 것
큰 L일 때:
→ 수용장이 넓어지며
→ 전역 정보 통합이 가능해지고 성능이 향상되는 현상을 보여주는 것

구체적으로, 각 계층의 합성곱 커널을 𝐰_l 활성화 함수를 ReLU (σ)라고 할 때, 출력은 다음과 같이 계산된다:

여기서 ŷ는 각 채널을 따라 선형 계층(linear layer)에 입력되며, 이 계층은 출력 채널 수 100개를 생성한다.
→ 이는 위에서 설명한 RNN 모델의 시간 프로젝션 결과와 동등한 크기이다.

최종적으로 이 선형 계층의 출력은
→ 각 픽셀에 대해 개별적으로 작동하는 ‘readout’ MLP에 입력되어
→ 클래스 로짓(class logits)을 생성하게 된다.

비지역 U-Net 기준 모델 (Non-local U-Net Baseline)

마지막으로, 국지 모델들의 성능에 대한 경쟁력 있는 비지역적 상한선(effective upper bound)으로서, U-Net 모델(Ronneberger 외, 2015)을 구현하여 분할 작업을 수행하게 한다.

간단히 말해, 이 모델은

4개의 인코더 계층: 공간 해상도를 점차 줄이고
4개의 디코더 계층: 공간 해상도를 다시 증가시키는 구조이다.
초기 채널 수는 c_in이며,
병목 구간(bottleneck)에서는 c_in × 2⁴ 채널에 도달한다.

특히 이 구조는 공간적 병목(spatial bottleneck)을 통해
→ 출력 계층의 각 픽셀 수용장이 전체 이미지를 포함하도록 만들기 때문에,
→ 시맨틱 분할(semantic segmentation) 과제를 단순하게 해결할 수 있게 해준다.

U-Net 모델의 경우에는, 디코더 네트워크 자체가 일종의 'readout' 역할을 하므로,
→ 최종 출력을 로짓(logit)으로 바로 사용한다.

이 모델은 가장 난이도 높은 데이터셋인 Multi-MNIST에 대해 평가된다.

그림 5: 진행파에 편향된 모델과 일반적인 국지 순환 모델 모두, 공간 정보를 통합하기 위해 진행파 동역학을 학습한다.

학습이 완료된 후, 특정 이미지(왼쪽)에 대해 LSTM과 NWM의 은닉 상태 변화(hidden state evolution) 중 일부를 시각화한 결과를 위쪽에 나타냈다. 여기서 우리는 시간이 지남에 따라 파동이 도형 전체에 걸쳐 전파되는 모습(wave propagation)을 확인할 수 있다. 아래쪽에는 은닉 상태의 시간적 동역학(hidden state time-dynamics)에 대해 픽셀 단위로 학습된 선형 투영(linear projection) 결과를 시각화하였다. 그 결과, 각기 다른 도형들이 서로 다른 차원 상에서 뚜렷하게 분리되어(pop out) 나타나는 것을 확인할 수 있다.

결과 (Results)

▪ Polygons

개념 증명의 초기 사례로서, 그림 3에서는 식 (11)의 NWM 모델이 FFT 기반 readout 방식으로 Polygons 데이터셋의 한 예제를 처리할 때의 은닉 상태 변화(hidden state evolution)를 시각화하였다. 이 예제에서 모델은 은닉 상태를 물체의 가장자리에서 사방으로 파동이 퍼져나가도록 초기화함을 확인할 수 있다. 시퀀스를 단순히 관찰해봐도, 도형 내부에서는 파동이 서로 다르게 전파되며, 그 결과 육각형 내부 각 지점의 주파수 표현(spectral representation)이 서로 구별되는 방식으로 변화하고 있음을 알 수 있다.

그림 4 (왼쪽)에서는, 테스트 이미지에 대해 모든 뉴런이 반응한 결과로부터 일부 푸리에 계수의 크기(Fourier coefficient magnitudes)를 시각화하였다. 그림 4 (오른쪽)에서는, 검증 세트 내에서 특정 클래스 라벨이 할당된 모든 픽셀에 대해 객체 클래스별 주파수 표현(frequency representations)을 평균하여 나타냈다. 이 결과들을 통해, 모델이 도형 간의 명확한 주파수적 차이를 포착하고 있으며, 이를 통해 모든 다각형을 99% 이상의 정확도로 식별할 수 있음을 확인할 수 있다. Polygons 데이터셋에서의 추가적인 결과 분석은 부록(Appendix)의 그림 6 및 7에 제시되어 있다.

Tetrominoes & MNIST

국지 순환 모델(local recurrent models)의 다양한 readout 방식과, 수용장 크기(receptive field)가 다른 피드포워드 모델(feed-forward models)을 비교하기 위해, 표 1(Table 1)에는 Tetrominoes와 MNIST에서 학습된 총 300개의 모델 결과가 집계되어 있다. 예상대로, 2층 및 4층 CNN은 두 데이터셋 모두에서 성능이 낮았으며, 수용장이 커질수록 성능이 향상되었다. 이러한 성능 향상은 특히 다음과 같은 경우에서 가장 두드러졌다:

MNIST: 16층 CNN (유효 수용장 33)
Tetrominoes: 8층 CNN (유효 수용장 17)

그러나,

MNIST에서는 32층 CNN,
Tetrominoes에서는 16층 및 32층 CNN에서 평균 성능이 다시 하락하였다.
다만, 분산은 여전히 높게 유지되었다.

이는 깊은 네트워크일수록 파라미터 수가 많고 최적화가 어려워, 학습 수렴이 불안정해지는 경향이 있기 때문이다. 그럼에도 불구하고, 최고 성능(peak performance)은 층 수가 많을수록 향상되는 경향을 보였으며, 이는 학습 실패율이 더 높더라도 일부 실험에서는 뛰어난 결과가 나왔음을 시사한다. 최소, 최대, 중앙값 성능은 보충 자료의 표 5 및 6에 제시되어 있다.

순환 모델 중에서는,

선형 투영(linear projection)을 사용하는 모델들이 가장 우수한 성능을 보였으며,
그중에서도 NWM이 다른 기준 모델들을 뛰어넘는 성능을 나타냈다.

반면,

마지막 은닉 상태만을 사용한 모델은 가장 낮은 성능을 보였다.
NWM은 분산이 가장 낮아, 학습 안정성(training stability) 면에서도 강점을 보였다.

그림 5는 샘플 이미지에 대한 순환 은닉 상태 및 선형 투영 결과를 시각화한 것이다.
흥미롭게도, LSTM은 명시적인 inductive bias가 없음에도 불구하고 파동 동역학을 자발적으로 학습하는 모습을 보였다.

Multi-MNIST

가장 인상적인 결과로, 표 2(Table 2)에서는 54K 파라미터를 가진 NWM 모델이, 30K 및 68K 파라미터를 가진 U-Net 모델보다 더 나은 성능을 보였다. 이는 NWM이 skip connection 없이, 국지 연결만으로 이루어졌다는 점에서 특히 주목할 만하다. 또한, NWM은 122K 및 190K 파라미터를 가진 U-Net 모델보다도 약간 낮은 성능만을 보이며, 비교적 작은 규모로도 경쟁력 있는 성능을 유지하고 있다. 또한 NWM은 모든 모델 중에서 foreground loss가 가장 낮았으며, 이는 다른 모델에 비해 예측(예: background)에 대한 신뢰(confidence)가 높아서일 가능성이 있다. 마찬가지로, NWM은 분산이 매우 낮아, 동급 U-Net 모델보다 훨씬 더 안정적인 학습 과정을 보였다는 점도 확인할 수 있다.

이러한 결과는,

시간 축에 대해 선형 readout을 수행하는 파동 동역학 기반 모델이
U-Net 스타일 아키텍처에 대한 강력하고 효율적인 대안이 될 수 있음을 시사한다.
특히 인공 신경망에서 공간 정보를 통합하는 새로운 접근으로서의 가능성을 보여준다.

표 1: 시간 시계열 기반 readout을 사용하는 국지 제약 순환 모델(locally constrained recurrent models)은, 전역 정보가 필요한 픽셀 단위 시맨틱 분할(semantic segmentation) 작업을 성공적으로 수행할 수 있다. 가장 낮은 foreground loss를 기록한 모델은 굵게 표시되어 있다. Arch (architecture)는 CNN 계층 수와, LSTM 및 NWM에 대한 readout 방식의 유형을 의미한다. 결과는 10개의 무작위 시드로 실험한 평균 ± 표준편차(mean ± std) 형식으로 표기되어 있다.

표 2: 파동 기반 모델(wave-based models)은 보다 어려운 Multi-MNIST 분할 과제에서, 유사한 규모의 U-Net 모델들보다 더 우수한 성능을 보인다. U-Net #c는 첫 번째 계층의 출력 채널 수(feature map 수)를 나타내며, 이후 각 계층마다 채널 수가 2배씩 증가한다. #θ는 전체 모델 파라미터 수를 의미한다. 표의 행은 #θ(파라미터 수) 기준으로 정렬되어 있으며, 결과는 12개의 무작위 시드로 실험한 평균 ± 표준편차(mean ± std) 형식으로 표시되어 있다.

한계 및 향후 연구 (Limitations & Future Work)

우리는 위 실험들을 통해, 진행파(traveling waves)가 시간 축을 통해 공간 정보를 통합하는 효과적이고 효율적인 메커니즘이라는 점을 충분히 입증했다고 믿지만, 이 접근법에는 본질적인 한계들도 존재한다. 우선 머신러닝 관점에서, 파동 기반 모델이 이 논문에서 제시한 Multi-MNIST 과제에서 파라미터 수가 유사한 U-Net보다 더 높은 성능을 보일 수 있음에도 불구하고, 현재 하드웨어에서는 실행 시간이 훨씬 오래 걸린다.
→ 이는 파동 동역학(oscillatory wave dynamics)을 정확히 수치적으로 적분해야 하며(Δt가 작아야 함),
→ 반면 U-Net 계열 모델은 GPU 병렬 처리에 최적화되어 있기 때문이다.

향후 연구에서는, 진동 기반 상태공간 모델(oscillatory state space models) (Rusch & Rus, 2025)을 활용하여 순환적 NWM 동역학을 시퀀스 길이에 대해 병렬 처리할 수 있는 가능성을 탐색할 예정이다.
→ 이를 통해 현재의 계산 병목(computational bottleneck)을 크게 완화할 수 있을 것으로 기대된다.

신경과학 관점에서,
우리가 제안한 파동 기반 모델은 피질 시트(cortical sheet)의 구조를 고도로 추상화한 이상화 모델이기 때문에
→ 계산적으로는 다루기 쉽지만,
→ 자연 진동수(natural frequency)나 감쇠 계수(damping parameter)와 같은 일부 파라미터들이
실제 신경생물학적 구성요소에 어떻게 대응되는지는 불분명하다. 그럼에도 불구하고, 본 모델은 과제 중심(task-oriented) 방식으로 파동 동역학을 학습할 수 있는 드문 사례 중 하나이므로, 향후 연구에서는 이 프레임워크를 활용해 실제 신경 기록과의 비교를 보다 정밀하게 진행할 계획이다.

마지막으로, 비록 본 연구는 “드럼의 모양을 들을 수 있는가?”(hearing the shape of a drum) 문제에서 영감을 얻었지만,
→ 우리가 훈련한 모델이 실제로 그 방식대로 이미지를 표현하고 있다고 보장할 수는 없다.
다만, 이 유추는 모델 설계를 이끄는 데 유용한 직관을 제공하며, 시간 기반 readout의 성공이 이 직관을 어느 정도 뒷받침해 준다. 하지만 우리는 독자들이 이 유추를 모델의 작동 원리를 문자 그대로 해석하는 것에는 주의하길 바란다.

결론 (Conclusion)

이 논문에서는 이론적 근거와 실험 결과를 통해,

진행파(traveling waves)가 국지적 제약(local constraint)을 갖는 신경망 구조 내에서 시간 차원을 통해 공간 정보를 통합할 수 있는 메커니즘이 될 수 있으며, 전역 연결 모델들과 비슷한 성능을 달성할 수 있음을 보여주었다.

또한,

파동 기반 정보(wave-encoded information)는 대부분의 기존 recurrent 모델들과 달리, 은닉 상태의 시계열에 대한 선형 투영(linear projection)을 통해 가장 직접적으로 활용 가능하다는 점도 실증적으로 밝혔다.

우리는 Conv-LSTM처럼 파동 동역학에 사전 편향이 없는 모델조차,

효과적인 공간 정보 전달을 위해 스스로 진행파를 학습한다는 사실을 보여주었으며,
→ 이는 파동 및 파동 기반 표현이 이러한 제약 조건 하에서 정보 전달의 최적 해법이 될 수 있음을 시사한다.

마지막으로, 우리는

파동 기반 정보 통합 방식이, 안정적이고 파라미터 효율이 높은 대안으로서
흔히 사용되는 U-Net 아키텍처와 경쟁할 수 있음을 보여주었다.

주목할 점은,

이러한 파동 기반 해법은 본질적으로 공간 도메인과 주파수 도메인 모두에 걸쳐 작동하기 때문에,
→ 신경과학에서는 EEG 또는 MEG와 같은 뇌파 기반 측정값과 더 직접적으로 연관될 수 있고,
→ 머신러닝 측면에서는 글로벌 self-attention 구조의 계산 병목을 해결하는 데 도움이 될 수 있다는 가능성도 제시한다.

우리는 이 연구가

생물학적 시스템과 인공 시스템 모두에서 파동 기반 표현이 전역적으로 과제 관련 정보를 전달할 수 있다는 생각에 대한 관심을 불러일으키고,
→ 이 분야의 후속 연구를 활성화하는 계기가 되기를 바란다.

'인공지능' 카테고리의 다른 글

Symbolic Discovery of Optimization Algorithms (2)	2025.05.07
Descanning: From Scanned to the Original Images with a Color Correction Diffusion Model (3)	2025.05.03
EdgeNeXt: Efficiently Amalgamated CNN-Transformer Architecture for Mobile Vision Applications (2)	2025.04.30
LLMs can see and hear without any training (2)	2025.04.28
Reasoning Models Can Be Effective Without Thinking (2)	2025.04.25

JunHan's AI Factory