우리는 지금까지 모델 구조에 대해서 이야기했다. 안에 들어가는 변수들에 대한 조정을 크게 다루지 않았다. 예를들어, Learning rate, Momentum rate, Dropout, Normalization, Number of layers, number of nodes에 대해서 말이다. 하지만 이 변수들을 효과적으로 setting하는 방법이 있을까? 현재는 없다고 알고 있다.
예시를 한번 들어보자.
우리가 3-layer perceptron을 만들었다고 하자. 그렇다면 다음의 hyperparameter들을 최적화해야 될 것이다.
• Learning rate: 𝜂
• Momentum rate: 𝑟
• Dropout probability: 𝑝
• Number of nodes in the first hidden layer: 𝑚
• Number of nodes in the second hidden layer: 𝑛
그렇다면 우리의 NN의 정확도는 𝜂, 𝑟, 𝑝, 𝑚, 𝑛의 함수이다. 즉, 다음의 식이 나온다.

결국 최적화를 위한 솔루션은 다음의 식이 되어야한다.

문제점은 다음과 같다.
• 𝑓 𝜂, 𝑟, 𝑝, 𝑚, 𝑛의 특정 정답이 무엇인지 모르겠다
• 일부 설정에 대해 평가할 수 있지만 신경망을 훈련해야 하기 때문에 평가 비용이 매우 비싸다
즉, 다음 그림과 같이 경험적으로 진행되어야 한다는 것이다.

그래도 이 비용을 최소로 하는 방법을 찾아보자.
Random하게 하다보면 나오지 않을까?와 하이퍼파라미터 탐색 공간을 정해두고 이를 다 찾아보는 방법 이렇게 두개가 바로 떠오른다. 즉, Random search, Grid search이다.
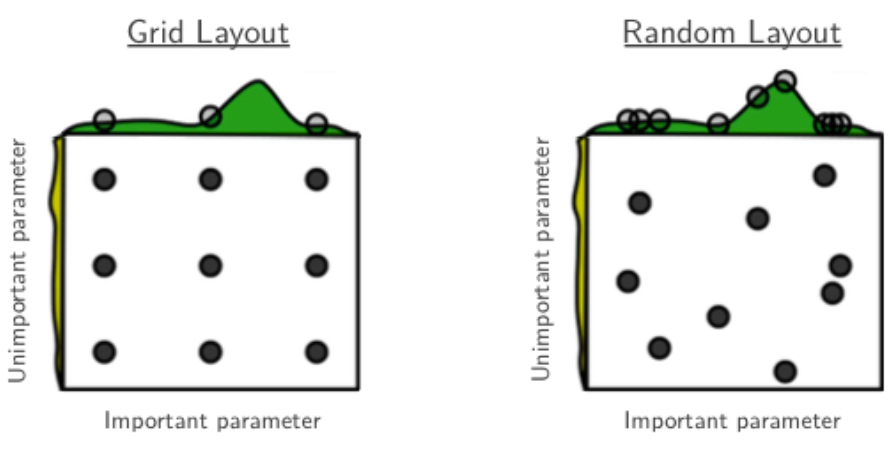
Random search은 운에 맡기는 것을 바로 알 수 있다. Grid search는 무엇일까?
첫 번째 하이퍼파라미터는 "learning_rate"이고, 가능한 값으로 0.001, 0.01, 0.1을 가질 수 있다. 두 번째 하이퍼파라미터는 "batch_size"이고, 가능한 값으로 16, 32, 64를 가질 수 있다. 이렇게 가정하면 모든 조합을 아래처럼 해보는 것이다.
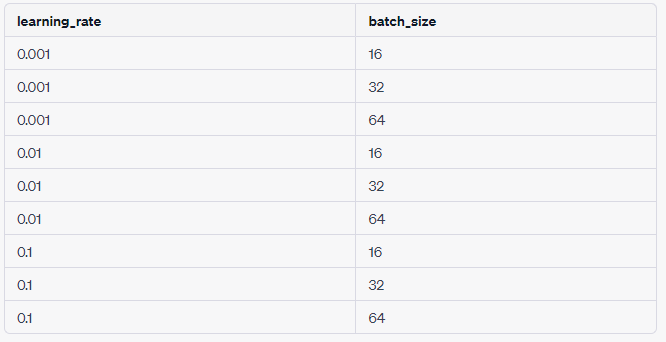
하지만 이 두 방법 모두 전혀 효율적이지 않다. 그렇다면 더 효율적이고 좋은 방법은 없을까?
그나마 고안된 방법은 다음과 같다.
가우시안 분포를 통해 알려진 데이터 포인트로 기본 함수 추측하고, 추측을 기반으로 쿼리할 다음 포인트를 선택한다. 그리고 이를 찾을 때까지 반복하는 것이다.

Gaussian Process에 대해서 좀 더 자세히 알아보자.
이를 시작하기 전에 Parametric Models과 Non-parametric Models에 대해서 알고가자.
Non-parametric model은 parametric model 과 다르게 model의 구조를 가정하지 않고,데이터로부터 모든 것을 알아낸다.
즉, 다음의 예시가 더 직관적일 것이다.
Parametric models:
– Linear Regression
– GMM
Non-parametric models:
– KNN
– Kernel Regression
– Gaussian Process

Gaussian Distribution (Normal Distribution)을 알아야한다. 가우시안 분포는 평균(mu)과 표준편차(sigma)라는 두 개의 매개변수를 가지며, 그래프 형태는 종 모양의 대칭적인 형태를 가지는 종 모양 곡선으로 표현된다. 분포의 중심은 평균(mu)이며, 표준편차(sigma)는 분포의 폭을 조절한다.

Covariance(공분산)에 대해서도 알아야한다. 공분산은 두 변수의 상호 변동성을 나타내며, 두 변수 간의 선형 관계의 강도와 방향성을 나타냅니다. 공분산의 값은 양수, 음수 또는 0이 될 수 있으며, 각각 다른 의미를 가지고 있다.
- 양수 공분산: 양수 공분산은 두 변수가 함께 증가하거나 감소하는 경향이 있음을 의미한다. 즉, 한 변수가 상승할 때 다른 변수도 상승하는 경향을 보인다.
- 음수 공분산: 음수 공분산은 한 변수가 증가할 때 다른 변수가 감소하는 경향을 나타낸다. 한 변수가 상승하면 다른 변수는 하강하는 경향을 보인다.
- 0 공분산: 0 공분산은 두 변수 사이에 선형 관계가 없음을 나타낸다. 즉, 한 변수의 변화가 다른 변수와 관련이 없다.
공분산은 변수 간의 스케일에 영향을 받기 때문에, 단위에 따라 값이 크게 달라질 수 있다. 이를 보완하기 위해 공분산의 정규화된 버전인 상관계수(correlation coefficient)가 사용된다. 상관계수는 -1에서 1 사이의 값을 가지며, 두 변수 간의 선형 관계를 정량화하여 해석하기 쉽게 해준다.

Covariance Matrix(공분산 행렬)에 대해서도 알아야한다. 공분산 행렬은 주어진 데이터 집합에서 변수들 간의 공분산을 계산하여 행렬 형태로 표현한 것이다. 행렬의 대각선 원소는 각 변수의 분산을 나타내며, 대각선을 기준으로 대칭 구조를 가지고 있다. 대각선 아래/위 원소는 각 변수들 간의 공분산을 나타낸다.
공분산 행렬은 데이터 집합의 특성을 파악하고 이해하는 데 도움을 준다. 행렬의 대각선 원소는 각 변수의 분산을 제공하여 변수의 변동성을 측정한다. 대각선 아래/위 원소는 변수들 간의 관계를 나타내며, 양수 값은 변수들 간의 양의 관련성을, 음수 값은 변수들 간의 음의 관련성을 나타낸다. 0 값은 두 변수 사이에 선형 관계가 없음을 의미한다.

Posterior Gaussian Distribution에 대해서도 알아야한다.
Posterior Gaussian Distribution는 베이즈 통계학에서 사전 분포(prior distribution)와 데이터를 통해 얻은 가능도 함수(likelihood function)를 조합하여 얻은 사후 분포(posterior distribution)의 형태로서 가우시안 분포를 따르는 분포다.
베이즈 통계학에서 사후 분포는 사전 분포와 가능도 함수를 베이즈 정리를 통해 조합하여 얻게된다. 사전 분포는 사전 지식이나 믿음에 기반하여 모델링되며, 가능도 함수는 주어진 데이터와 관련된 확률 모델이다. 베이즈 정리는 이러한 사전 분포와 가능도 함수를 조합하여 사후 분포를 계산하는 역할을 한다.

하지만 이걸가지고도 우리가 예측할 수 있는 것은 한정되어있다. 설명해보겠다.
모르는 함수 f(x)를 추정하기 위해서 모든 x에 대해서 f(x)를 확률변수라고 가정해보자. f(x)는 다음 확률 분포를 따른다고 가정하자. 그렇다면 다음이 정리된다.
– f(x) ~ N(0, 1)
– 가장 일반적인 분포가 Gaussian이니까 이것에 따른다하자
– f(x)가 무슨 값일지 모르니 그 평균은 0일테고, 분산은 다른 값으로 해도 되지만 우선 1이라고 하자
그러면, f(1)=1라고 하면, f(2)의 값은 얼마일까?
확률변수 f(1)과 f(2) 사이에 correlation이 좀 있다고 해보자.
예를 들면 f(1)이 평균에서 1정도 떨어진 값이 관찰되었다면 f(2)는 평균에서 0.7 정도 떨어진 값이 관찰된다고 하자.
– 즉, f(1)과 f(2)의 covariance는 0.7임으로 다음과 같이 나타낼 수 있다.
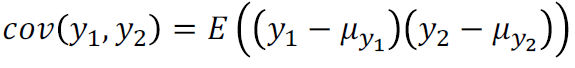
(f(1), f(2))는 bivariate Gaussian distribution을 따른다고 하지면 아래의 수식과 같다.
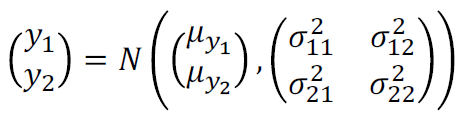
y1 = f(1), y2 = f(2)라고 하고 각 공분산을 대입하면 다음의 수식형태가 나온다.
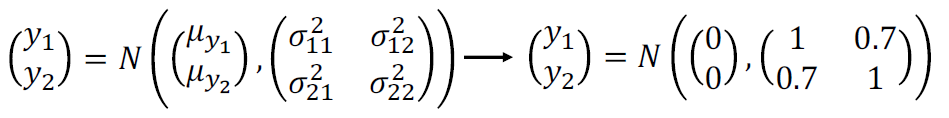
우리는 y1=1로 알고 있으니까 다음식이 나온다.

그렇게 계산하면 다음과 같은 결론이 나온다.
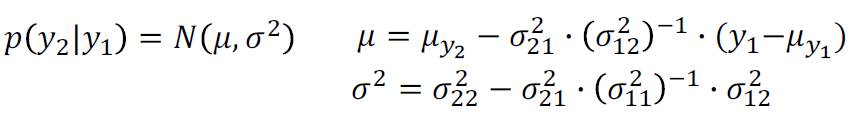
따라서 우리는 f(2)의 분포를 알아 낼 수가 있다.
하지만 이럼에도 문제점이 발생한다. f(x1)과 f(x2)의 공분산을 어떻게 알 수 있을까?
사실 알 수가 없다. 그러니까 가정을 하나 추가해보자.
– x1과 x2가 similar 할수록 f(x1)과 f(x2)는 유사한 값을 가진다
• x1과 x2가 가까워질수록 f(x1)과 f(x2)의 covariance는 커진다
– x1과 x2가 덜 similar 할수록 f(x1)과 f(x2)는 다른 값을 가진다
• x1과 x2가 멀어질수록, f(x1)과 f(x2)의 covariance는 작아진다
– 일반적으로 위의 가정에 부합하는 함수를 하나 정의해서 공분산으로 사용한다. 예를 들면,

결국은 다음이 되는 것이다.

즉, 우리가 초기에 설정한 가정과 일치한다.
결론적으로 x가 1에 가까우면 당연히 f(x)는 1에 가까워질 것이고, 멀어지면 더 불분명해진다고 할 수 있으니까 말이다.

이때 f(x)의 uncertainty는 아래처럼 표시할 수도 있다.
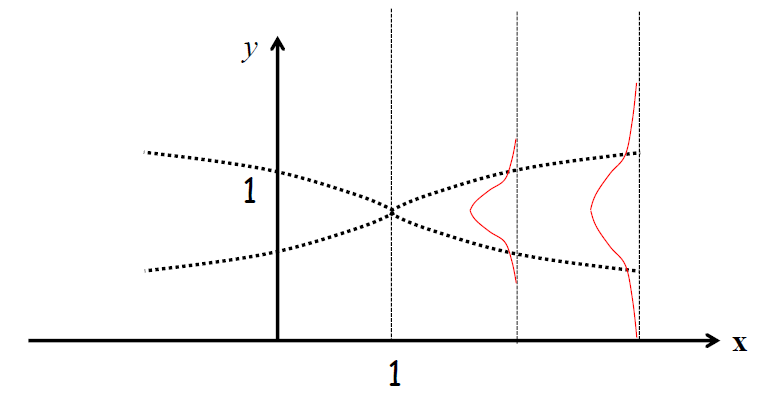
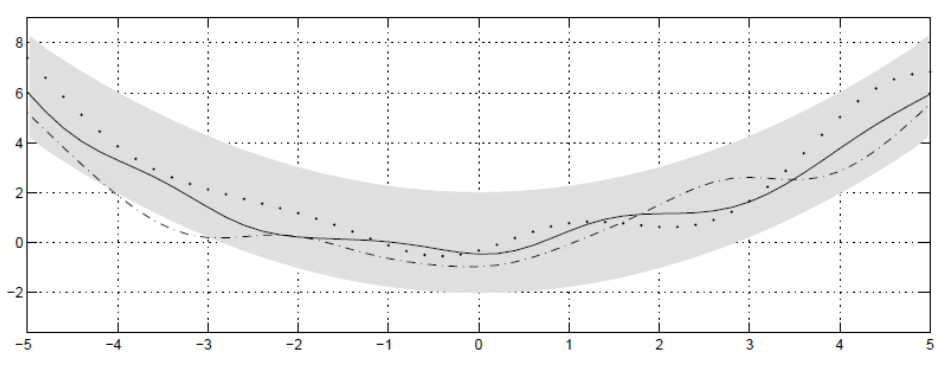
그렇다면 우리가 두 지점의 값을 알고 있다면, 다른 지점의 값은 아래와 같이 분포한다고 할 수 있다.

결국 더 많은 지점의 값을 알수록 f(x)를 더 잘 추정할 수 있다.

관찰한 값이 n개일 때의 경우로 확장하면, Gaussian Process이다.

복잡하게 말한것 같은데, 결론은 간단하다. Covariance 함수가 바뀌면 추정되는 함수의 모양이 바뀌기 떄문에 Covariance 함수는 사용자가 잘 선택해야 합니다.
즉, 가우시안 프로세스는 랜덤 변수의 모음이며 다음을 만족하는 무한한 숫자들의 모음으로 바라봐야합니다.

따라서 A distribution over functions은 다음과 같다.
– 임의의 변수 모음 == 함수
정리하면 다음과 같다.
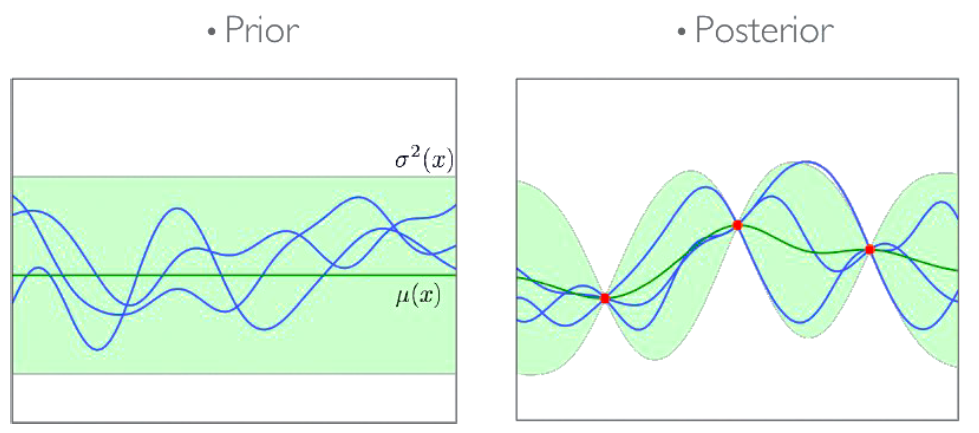
가우시안 프로세스는 무한한 개수의 확률 변수로 이루어진 확률 분포를 모델링하는 방법으로, 모든 변수들이 결합적으로 가우시안 분포를 따르는 분포이다. Prior Gaussian Process는 입력 변수(예: 공간 또는 시간)에 대한 아무런 정보가 없을 때의 가우시안 프로세스를 나타낸다. Prior Gaussian Process는 모든 입력 위치에서의 확률 분포를 정의하며, 평균 함수와 공분산 함수로 설명된다. Prior Gaussian Process는 모델링의 초기 상태로 사용되며, 입력에 대한 아무런 관찰이 이루어지지 않은 상태를 의미한다.
반면, Posterior Gaussian Process는 Prior Gaussian Process에 관측된 데이터를 반영하여 업데이트된 확률 분포를 나타낸니다. 즉, 입력 변수에 대한 관찰 데이터가 있는 경우, Prior Gaussian Process를 데이터와 결합하여 조건부 확률 분포를 계산한 것이다. Posterior Gaussian Process는 Prior Gaussian Process의 평균과 공분산을 조정하여 데이터에 대한 정보를 포함한 업데이트된 분포를 제공한다. Posterior Gaussian Process는 관측된 데이터에 대한 예측, 불확실성의 추정, 미래 값의 샘플링 등 다양한 추론 작업에 사용된다.
Prior Gaussian Process와 Posterior Gaussian Process는 가우시안 프로세스를 통해 모델링된 확률 분포의 두 가지 형태를 나타낸다. Prior Gaussian Process는 입력 변수에 대한 아무런 관측이 없을 때의 초기 확률 분포를 나타내며, Posterior Gaussian Process는 입력 변수에 대한 관측 데이터를 반영하여 업데이트된 확률 분포를 나타낸다. Prior Gaussian Process는 모델의 초기 상태를 나타내며, Posterior Gaussian Process는 데이터를 통한 업데이트된 분포를 나타낸다.
결론적으로 왜 Gaussian Process가 좋은가를 말하면서 이 파트를 끝낸다.
– 예측의 uncertainty 를 수치화 할 수 있다
– 여러 model selection 과 hyperparameter selection 과 같은 Bayesian method를 그대로 사용할 수 있다
– input point 에 대한 임의의 함수를 모델링한다 (No model assumption)
그렇다면 Hyperparameter Optimization을 Bayesian Optimization으로 최적화 해보자.
다음 Query를 선택하려면 어떻게해야되나?
기대값이 좋다면 Exploitation, 기대값이 불확실성을 나타내면 Exploration이 진행되어야 한다.
Acquisition Function 𝜶(𝒙)를 사용해서 이를 해석해보면, 다음 지점 선택을 위해서는 아래의 함수를 만족시켜야한다.
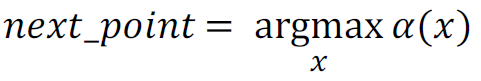
Acquisition Function의 필요사항은 Exploitation과 Exploration의 balance와 쉽게 optimize가 가능해야한다.
그렇다면 𝜶(𝒙)를 어떻게 optimize 해야될까?

위의 방법들을 사용하면 된다. 추가적으로 설명하면 다음과 같다.
Closed-Form Acquisition Functions는 계산이 닫힌 형태로 표현되어 있어 효율적으로 계산할 수 있다. 이 중에서 세 가지 일반적인 함수인 "Probability of Improvement (PI)", "Expected Improvement (EI)", 그리고 "GP Upper (Lower) Confidence Bound"가 널리 사용된다.
Probability of Improvement (PI):
Probability of Improvement은 현재까지의 최적 솔루션보다 우수한 결과를 얻을 확률을 측정하는 함수다. PI는 최적 솔루션의 예측 값과 해당 위치의 불확실성(표준 편차)을 고려하여 계산된다. 즉, 더 높은 확률 값을 가진 지점을 선택하여 성능을 향상시키는 방향으로 탐색한다.
Expected Improvement (EI):
Expected Improvement은 현재까지의 최적 솔루션과 비교하여 기대 성능 향상을 계산하는 함수다. EI는 가능한 모든 결과에 대한 확률 가중 평균으로 계산된다. 불확실성(표준 편차)과 성능 향상의 기대값을 함께 고려하여, 더 큰 기대 향상을 가진 지점을 선택한다.
GP Upper (Lower) Confidence Bound:
GP Upper Confidence Bound는 가우시안 프로세스(Gaussian Process)의 상한(또는 하한)을 계산하여 탐색할 위치를 결정하는 함수다. 상한(또는 하한)은 예측 값에 대한 불확실성(표준 편차)의 곱으로 계산된다. GP Upper Confidence Bound는 불확실성이 높은 지점을 탐색하며, 모델의 불확실성을 최대한 활용하여 샘플링 위치를 결정한다.
이러한 Closed-Form Acquisition Functions은 베이지안 최적화에서 탐색과 활용의 균형을 유지하며, 효율적인 탐색과 샘플링을 지원한다. 각 함수는 모델의 예측 값과 불확실성을 고려하여 샘플링할 위치를 결정하는데 사용되며, 목적에 따라 선택될 수 있다.
요약하자면, Closed-Form Acquisition Functions인 Probability of Improvement, Expected Improvement, GP Upper (Lower) Confidence Bound는 베이지안 최적화에서 사용되는 함수로, 다음으로 샘플을 쿼리할 위치를 결정하는 데 활용된다. 각 함수는 현재까지의 최적 솔루션과 예측 값, 불확실성 등을 고려하여 탐색과 활용을 균형있게 조절한다.
Bayesian Optimization은 다음 그림과 같이 작동한다.
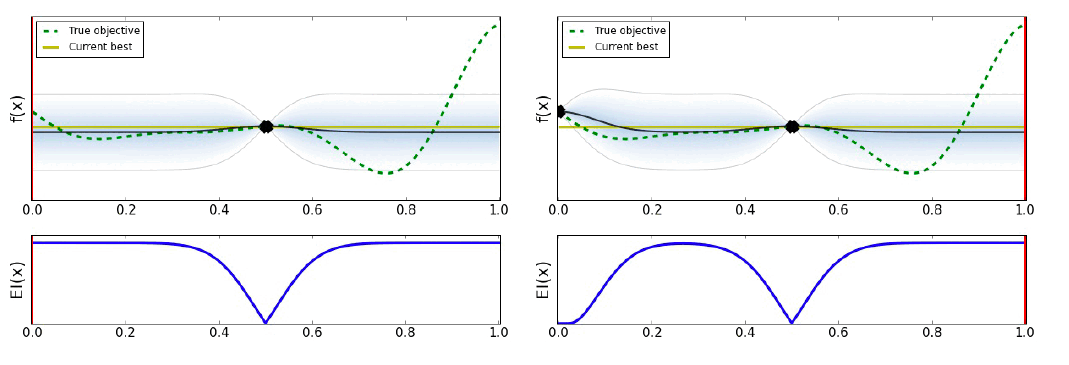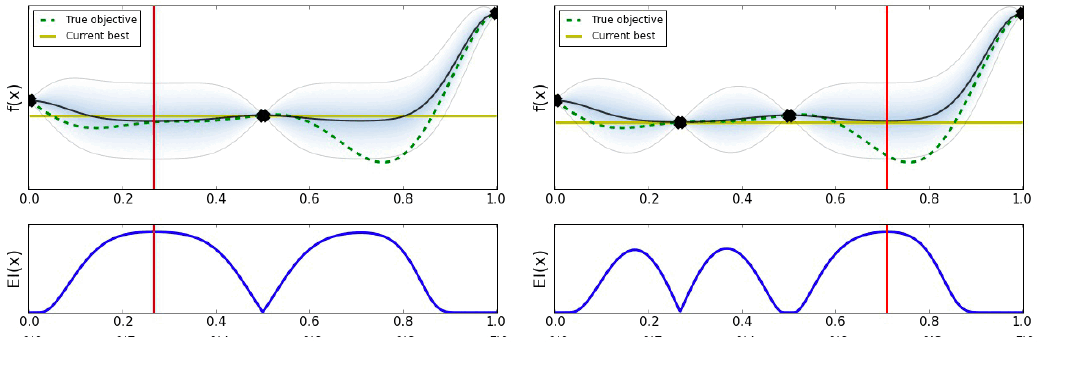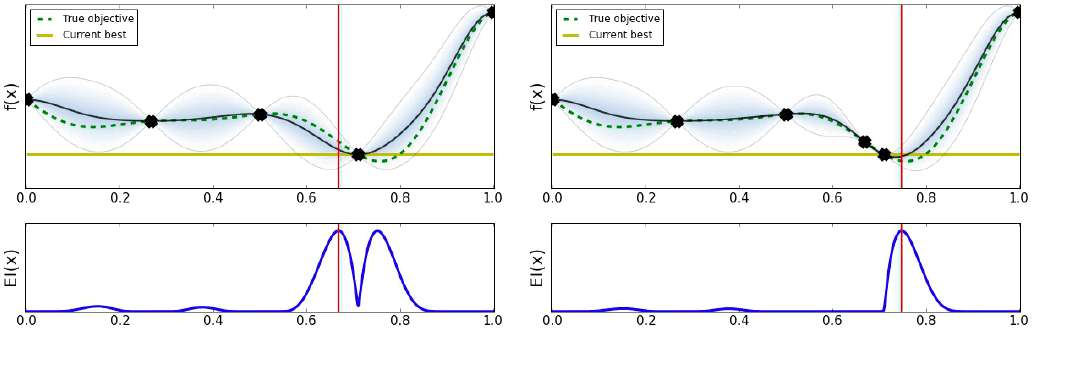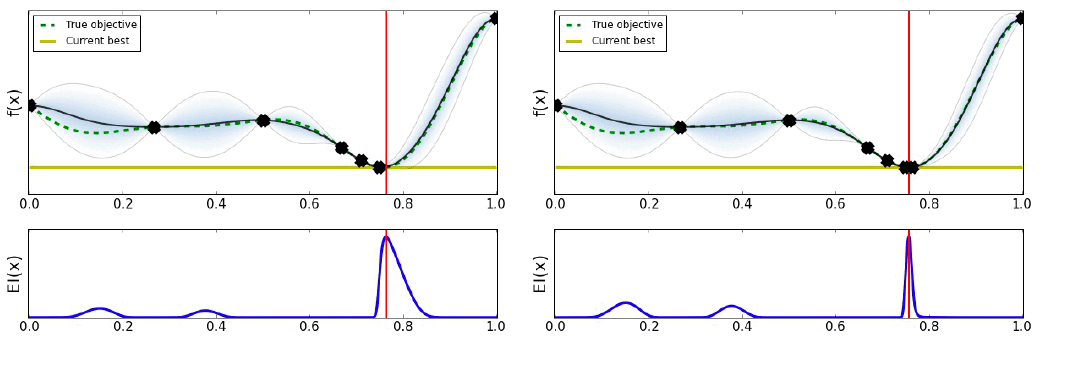



유틸리티의 선택은 최적화 결과를 많이 바꿀 수 있다. 아래의 그림과 같이 말이다.

최고의 효용은 문제와 필요한 탐색/이용 수준에 따라 다르다.
Acquisition Function 최적화하는 법은 다음과 같다.
Gradient descent methods
– Eg: Conjugate gradient.
Lipschitz based heuristics
– DIRECT
Evolutionary algorithms
이외에도 다른 방법들이 있다.
우리가 알고 있는 Gradient descent method는 아래와 같이 작동한다.

DIRECT는 아래와 같이 작동한다.

DIRECT는 일반적으로 좋은 솔루션을 찾아내며, 기울기를 필요로하지 않는다. 그러나 비제곱 도메인에는 적용할 수 없다.
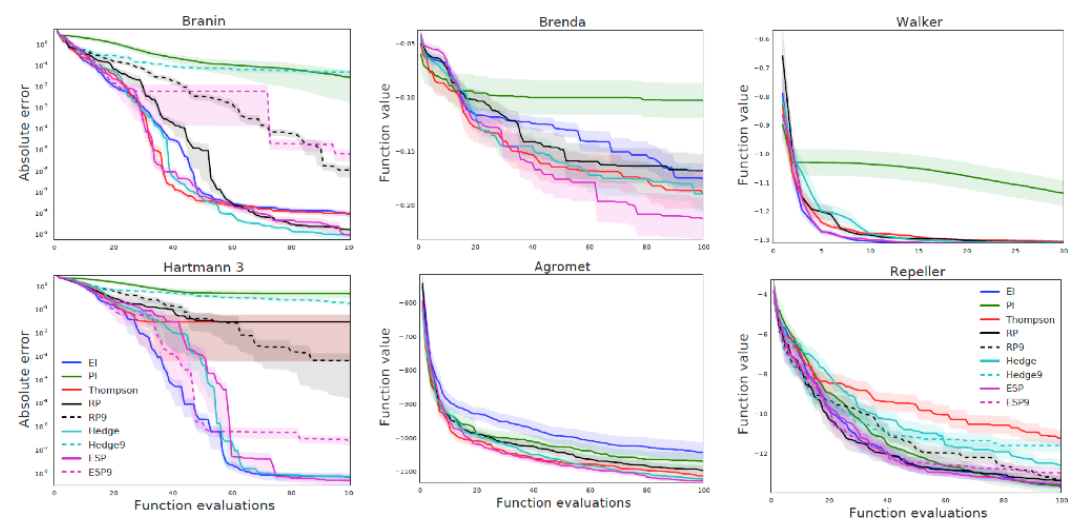
내가 언급했던 방법들의 Performance이다.


하지만 단점도 있다.
- 함수 모델이 잘못되면 재앙이 될 수 있다
- 실험은 순차적으로 실행되어 많은 시간을 잡아먹는다
- 차원 및 평가의 제한된 확장성이 있다
Covariance function 선택시 다음을 사용하면 좋다.
- 일반적으로 적응형 Matèrn 3/5 커널을 사용합니다

끝.
'인공지능' 카테고리의 다른 글
| LORA (0) | 2023.12.25 |
|---|---|
| Chapter 10 Various artificial intelligence (0) | 2023.05.20 |
| Chapter 8 Small Nets and EfficientNet (1) | 2023.05.20 |
| Chapter 7 Generative Adverislal Network (0) | 2023.05.20 |
| Chapter 6 Transformer Model (0) | 2023.05.20 |


