https://arxiv.org/abs/2511.09146
DoPE: Denoising Rotary Position Embedding
Rotary Position Embedding (RoPE) in Transformer models has inherent limits that weaken length extrapolation. We reinterpret the attention map with positional encoding as a noisy feature map, and propose Denoising Positional Encoding (DoPE), a training-free
arxiv.org
초록
Transformer 모델의 Rotary Position Embedding(RoPE)은 구조적으로 길이 외삽(length extrapolation)에 한계를 가지고 있다. 본 연구에서는 위치 인코딩이 적용된 어텐션 맵을 잡음이 포함된 feature map으로 재해석하고, feature map에서 이상치 주파수 대역(outlier frequency bands)을 검출하기 위해 절단된 행렬 엔트로피(truncated matrix entropy)에 기반한 훈련 불필요(training-free) 방식의 Denoising Positional Encoding(DoPE)을 제안한다. 또한 feature map의 잡음 특성을 활용하여, 추가 파라미터 없이(parameter-free) Gaussian 분포로 재파라미터화함으로써 강인한 길이 외삽 성능을 달성한다.
우리의 방법은 어텐션 싱크(attention sink) 현상의 근본 원인과 그것이 절단된 행렬 엔트로피와 연결되는 메커니즘을 이론적으로 규명한다. Needle-in-a-haystack 실험과 many-shot in-context learning 태스크에서 DoPE는 최대 64K 토큰에 이르는 확장된 컨텍스트 환경에서도 검색 정확도와 추론 안정성을 크게 향상시키는 것으로 나타났다. 결과적으로, 제안된 위치 임베딩 디노이징 전략은 attention sink를 효과적으로 완화하고 균형 잡힌 어텐션 패턴을 복원하여, 길이 일반화(length generalization)를 향상시키는 단순하면서도 강력한 해결책임을 입증한다.
1 서론
위치 인코딩(position encoding)은 대규모 언어 모델(LLM)의 핵심 구성 요소로, 토큰 간 상호작용에 중요한 영향을 미친다. 어텐션 스코어는 쿼리 벡터와 키 벡터의 내적(dot product)으로 계산된다.

일반적으로 위치 인코딩은 시퀀스의 순서를 반영하기 위해 쿼리와 키 벡터에 더해진다. 다양한 기법들 중 Rotary Position Embedding (RoPE) (Su et al., 2024)은 쿼리와 키를 회전 변환해 상대적 위치 정보를 곧바로 내적 연산에 반영할 수 있다는 장점으로 널리 사용된다. 이때 RoPE는 다음과 같이 적용된다.
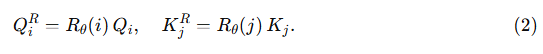
그러나 DAPE(Zheng et al., 2024)가 위치 인코딩을 어텐션 스코어 위 MLP로 대체하고, NoPE(Wang et al., 2024)가 어떠한 위치 인코딩도 사용하지 않는 방식을 제시한 것처럼, 기존 RoPE 방식이 Transformer(Vaswani et al., 2017) 성능을 제약할 수 있다는 연구들이 등장하고 있다.
본 연구에서는 위치 인코딩을 절단된 행렬 엔트로피(truncated matrix entropy)(Xiong et al., 2024)를 통해 잡음이 포함된 feature map으로 개념화한다. 우리는 feature의 잡음 수준을 측정하고, 추가 파라미터가 없는(parameter-free) Gaussian 분포 기반 재파라미터화를 통해 길이 외삽(length extrapolation)을 수행한다. 구체적으로 본 논문의 주요 기여는 다음과 같다.
• 절단된 행렬 엔트로피를 도입해 noisy head를 식별하고, 위치 인코딩을 파라미터 없이 Gaussian 분포로 모델링하여 길이 외삽 성능을 달성했다.
• 이론적·실험적으로, 어텐션 스코어 계산에 활용되는 위치 인코딩의 저주파 정렬(low-frequency alignment)이 attention sink 및 retrieval head 같은 구조적 희소 현상의 근본 원인임을 규명했다.
• 강력한 외삽 성능을 가진 어텐션 head는 공통적으로 low-rank 구조를 보이며, 이러한 head의 위치 인코딩은 유지하고 high-rank head의 위치 인코딩만 제거하면 학습 없이 최대 10포인트의 성능 향상을 얻을 수 있음을 발견했다.
2 배경
본 절에서는 먼저 Vaswani et al.(2017)의 Transformer 아키텍처를 개괄하며, 특히 멀티-헤드 어텐션 메커니즘에 초점을 맞춘다. 이후 Rotary Position Embedding(RoPE)이 어텐션 패턴을 형성하는 데 어떤 역할을 수행하는지 분석한다.
2.1 멀티-헤드 자기어텐션(Multi-Head Self-Attention)
여기서는 디코더 전용 Transformer로 구현된 인과 언어 모델(causal language model)을 고려한다. 토큰 표현

2.2 Rotary Position Embedding
대부분의 LLM은 기본적인 위치 인코딩 메커니즘으로 Rotary Position Embedding(RoPE)(Su et al., 2024)을 채택하며, 이는 현대 아키텍처에서 사실상의 표준(de facto standard)이 되었다. RoPE는 각 쿼리·키 벡터를 일련의 이차원 평면 상에서 회전시키는 방식으로 토큰의 위치를 인코딩한다. 이러한 수식화는 단순한 내적 구조(dot-product structure)를 유지하면서도 어텐션 스코어가 상대적 위치 차이(relative positional offsets)에 의존하도록 만들어 준다.


3 관련 연구
RoPE 기반 길이 외삽(Length Extrapolation With RoPE)
RoPE는 매우 널리 채택되어 왔다(Su et al., 2024). LLaMA2(Touvron et al., 2023), LLaMA3(Dubey et al., 2024), Qwen3(Yang et al., 2025)와 같은 모델들은 토큰 순서를 위치에 따라 각도가 달라지는 벡터 회전을 통해 인코딩한다. 그뿐 아니라 RoPE 및 그 파생 기법들은 Qwen(Bai et al., 2023), Qwen2(Team, 2024a), Qwen2.5(Team, 2024b), Qwen2.5-VL(Bai et al., 2025), Qwen3(Yang et al., 2025), Mistral(Jiang et al., 2023), Gemma(Team et al., 2024a), Gemma-2(Team et al., 2024b), Gemma-3(Team et al., 2025) 등 최근 공개된 대규모 모델 전반에서 폭넓게 사용되고 있다.
그러나 입력 길이가 학습 시 사용된 길이를 여러 배 초과하게 되면(Peng et al., 2023; Chen et al., 2023; Ding et al., 2024), 모델 성능이 심각하게 저하된다. 이러한 성능 저하는 RoPE만의 문제가 아니며, ALiBi(Press et al., 2021)나 Kerple(Chi et al., 2022) 같은 다른 위치 인코딩에서도 유사한 현상이 관측된다. 이를 해결하기 위해 다양한 접근법이 제안되어 왔다. 예를 들어 FIRE(Li et al., 2023)는 학습 가능한 위치 인코딩을 도입하여 긴 컨텍스트 성능 저하를 완화하는데, MLP를 사용해 적절한 위치 표현을 생성하는 방식이다. 반면 NTK 기반 방법들(Peng et al., 2023)은 주파수 스펙트럼을 수정해 컨텍스트 길이를 확장하고 긴 시퀀스에서의 안정성을 높이는 방식으로 길이 외삽을 개선한다.
위치 인코딩 없이 길이 외삽(Length Extrapolation Without Positional Encoding)
위치 인코딩은 시퀀스 정보를 부여하고 모델의 표현 능력을 향상시킨다(Shaw et al., 2018; Yun et al., 2019; Luo et al., 2022). 그러나 여러 연구(Zuo et al., 2024; Haviv et al., 2022; Köcher et al., 2025)는 인과 디코더 기반 Transformer가 명시적인 위치 인코딩이 없어도 토큰 순서를 암묵적으로 포착할 수 있음을 보여준다. 더 나아가 NoPE(Kazemnejad et al., 2023)는 causal mask 자체가 위치 관계를 본질적으로 암호화한다는 사실을 입증했다.
최근에는 DAPE(Zheng et al., 2024) 및 DAPE v2(Zheng et al., 2024)와 같은 데이터 의존적(data-dependent) 위치 인코딩 방식이 등장했다. 이 접근법들은 위치 인코딩을 어텐션의 입력 의존 feature map으로 간주하여 길이 외삽 성능을 향상한다. 그러나 이러한 기법들 역시 위치 인코딩을 구성하기 위한 학습 가능한 파라미터 행렬에 의존한다는 한계를 가진다.
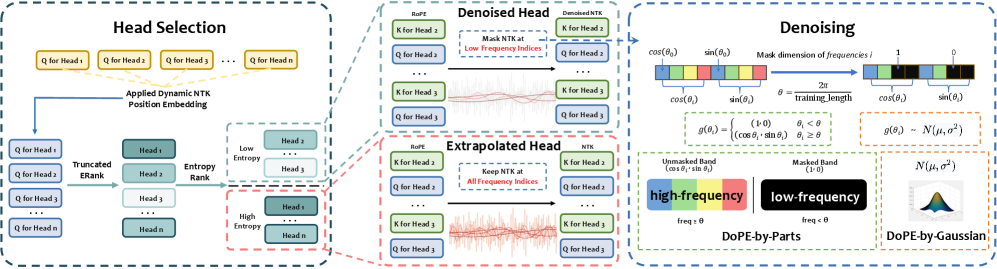
Figure 1:Visualization of DoPE
4 Denoising Positional Encoding
4.1 이상치 특성(Outlier Features)















🔥 문제 상황: RoPE가 특정 헤드에서 “스파이크”를 만들어 냄
RoPE가 잘못 동작하는 헤드는 어텐션 맵이 이렇게 됨:
정상 어텐션
[ . . . . . ]
[ . . . . . ]
[ . . . . . ]
[ . . . . . ]
[ . . . . . ]
스파이크/밴드가 생긴 어텐션
[ . . X . . ]
[ . . X . . ]
[ . . X . . ]
[ . . X . . ]
[ . . X . . ]세로줄/가로줄이 “밝게” 나타나면서
→ 모델이 특정 위치에 정착해버림
→ 긴 문맥에서 Attention Sink 발생
🎯 DoPE-by-Gaussian이 하는 일
문제 있는 헤드를 찾아서, 해당 헤드의 RoPE 위치 인코딩을 가우시안 랜덤 노이즈로 교체함.
아스키로 표현하면:
원래 RoPE로 회전된 Q/K (문제 헤드)
스파이크 방향 (RoPE)
→ → → → →Gaussian 노이즈로 교체
등방성(모든 방향 고르게 분포)
↗ ↓ ↙ ↑ ← ↘ →즉, 방향이 한쪽으로 쏠려 있는 벡터를
→ 여러 방향이 섞인 랜덤 벡터로 바꿔 균형 잡힘
💡 계산식의 의미를 직관적으로 바꾸면
m_h = 1 → 정상 헤드, 그대로 둠
m_h = 0 → 스파이크 헤드, RoPE를 Gaussian으로 바꾸기구현 형태를 단순한 아스키로 나타내면:
if m_h == 1:
K = RoPE(K) # 그대로 사용
Q = RoPE(Q)
else:
K = Gaussian() # 치환
Q = Gaussian()
직관적으로 그리면:
[스파이크] [DoPE-by-Gaussian 후]
||||| /\ ↖ ↓ → ↗ ↑ ←
한 방향 여러 방향 → 결집 깨짐🎤 한 줄 요약
DoPE-by-Gaussian은 스파이크가 생긴 헤드의 RoPE 방향성을 무시하고, 모든 방향으로 고르게 퍼진 랜덤 벡터로 대체하여 주파수/스펙트럼 균형을 되돌리는 방식이다.


표 2: Many-Shot In-Context Learning 과제에서 Qwen2.5-Math-7B 외삽 실험에 대해, 디노이징 전략의 실험 설정과 결과 요약.
모델은 컨텍스트 길이 4K에서 16K로 외삽되었으며, 실험은 nlile/hendrycks-MATH-benchmark 데이터셋 기반의 In-Context Learning(ICL) 구성으로 수행되었다.


표 3: Ablation 연구 — 서로 다른 시퀀스 길이에서 선택된 어텐션 헤드를 사용했을 때 64k 외삽 성능 비교.
각 실험 구성은 24k, 32k, 48k, 56k, 64k 길이의 시퀀스에서 식별된 헤드들을 사용하고, 이후 64k 작업을 Noisy 및 Vanilla 조건 모두에서 평가한다. 측정된 점수는 헤드 선택에 사용된 시퀀스 길이가 최종 성능에 어떤 영향을 미치는지를 보여준다.

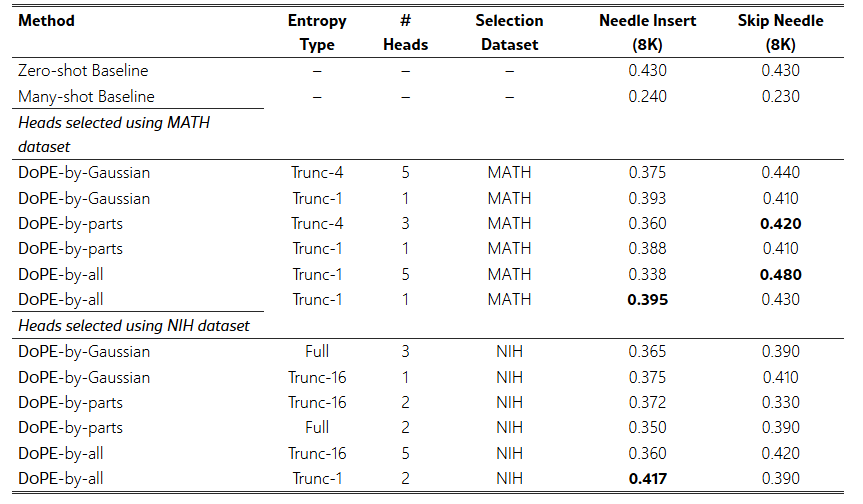
표 4: 어텐션 헤드 식별 방식에 대한 Ablation 연구.
이 표는 디노이징에 사용할 어텐션 헤드를 선택할 때 MATH 데이터셋을 사용하는 경우와 NIH 데이터셋을 사용하는 경우를 비교하고, 이후 many-shot in-context learning 성능을 테스트한 결과를 보여준다.
모든 실험은 Qwen2.5-Math-7B 모델, 8K 컨텍스트 길이에서 수행되었다.
헤드 선택은 Query 표현을 사용하고 post-NTK 기준으로 수행되었다.
표의 결과 값은 MATH 문제에 대한 정확도(accuracy)이며, 두 조건에서 측정된다.
- Needle Insertion: ICL haystack 내부에 정답이 삽입된 설정
- Skip Needle: 정답 삽입 없이 수행하는 베이스라인 설정
5 실험
5.1 실험 설정
"Needle-in-a-haystack" 합성(synthesis) 과제는 자연어 처리와 정보 검색 분야에서 특히 난이도가 높은 문제로 알려져 있다. 이 과제의 핵심은 방대한 양의 데이터 속에서 매우 드문 핵심 정보를 찾아내고 결합(synthesize) 하는 것이다. 원하는 정보는 양이 적을 뿐만 아니라, 매우 긴 문서나 여러 출처에 걸쳐 깊이 묻혀 있기 때문에 마치 건초 더미 속 바늘을 찾는 것과 같은 어려움을 가진다.
실험은 크게 두 가지 구성으로 나뉜다: original setups와 noisy setups.
Original Setups
베이스라인 실험에서는 needle(핵심 정보)을 컨텍스트 내부 다양한 위치에 삽입하고, 컨텍스트 길이는 24K와 64K 토큰의 세 가지 설정에서 평가된다. 이 구성은 모델이 컨텍스트 길이가 달라져도 특정 정보를 제대로 검색할 수 있는지를 살펴보기 위함이다.
Noisy Setups
반면, noisy 실험은 동일한 두 컨텍스트 길이(24K, 64K 토큰)에서 수행되지만, needle 주변에 attention sink를 유도하는 기호를 배치하여 인위적으로 교란을 추가한다.
이 표는 각 파라미터 조합에 대해 Noisy(64k)와 Original(64k) 설정에서 상위 3개의 결과만 필터링해 보여준다.
이 실험 설계는 모델이 노이즈가 존재하거나 신뢰도가 낮은 데이터 환경에서 얼마나 견고하고 안정적인지 체계적으로 평가할 수 있도록 하며, 현실 환경에서의 적용 가능성과 회복력(resilience)을 분석하는 데 도움을 준다.
또한 다른 서술 방식에서는 다음과 같이 표현된다.
Noisy 실험은 동일한 두 컨텍스트 길이(24K, 64K 토큰)에서 수행되지만, attention sink를 쉽게 유발하는 시작 토큰(start-of-sequence symbol) 등 노이즈 토큰을 needle 뒤에 삽입하여 비완벽한 조건을 모사한다.
이 실험 설계는 노이즈 또는 attention sink가 존재할 때 모델이 얼마나 성능을 유지하는지 평가할 수 있으며, attention sink 현상과 matrix entropy의 관계를 분석할 수 있도록 한다.


- NIH 과제에서는 목표 외삽 길이에 해당하는 시퀀스에서 헤드를 선택한다.
예: 64K 시퀀스에서 식별된 헤드를 64K 평가에 사용 (표 3 참고) - Many-shot In-Context Learning 과제에서는
MATH 데이터셋과 NIH 데이터셋 각각으로 계산된 엔트로피 점수를 사용해 헤드를 선택,
이를 교차 적용하여 과제 간 전이 가능성(transferability)을 평가한다 (표 4 참고)
기타 실험 환경
모든 실험은 SGLang (Zheng et al., 2023) v0.5.3rc0에서 수행되며, 백엔드는 FlashAttention-3 (Shah et al., 2024)을 사용한다. 멀티-GPU 추론이 필요할 경우 tensor parallelism을 사용하며, 동적 컨텍스트 길이 지원을 위해 CUDA graphs는 비활성화(disabled) 되어 있다.
(a) Vanilla Matrix Entropy 기반 DoPE

(b) Truncated Matrix Entropy 기반 DoPE
그림 2: 전체 헤드와 상위 16개 헤드(depth 0)에 대해 어텐션 가중치 엔트로피를 비교한 결과.
5.2 주요 결과
실험은 original setups과 noisy setups 두 가지 설정에서 수행되었으며, 결과는 표 1에 정리되어 있다. 주요 관찰 내용은 다음과 같다:
- attention sink 토큰을 삽입하면 성능이 급격히 저하된다.
즉, noisy 환경에서는 모델의 성능 붕괴가 뚜렷하게 관찰된다. - 짧은 컨텍스트(24k tokens)에서는 Gaussian 노이즈를 위치 인코딩에 추가하는 DoPE가 최고 성능을 달성했다.
베이스라인 75.417에서 84.354까지 향상되었다.
이는 포지션 인코딩이 레이어를 거치며 누적될수록 Gaussian 분포의 형태로 근사된다는 통찰을 간접적으로 뒷받침한다. - Truncated matrix entropy와 vanilla matrix entropy는 동작 패턴이 분명히 다르다.
- Truncated matrix entropy의 경우 내림차순 정렬 후 저엔트로피 헤드를 제거한다.
- Vanilla matrix entropy의 경우 오름차순 정렬 후 고엔트로피 헤드를 제거한다.
두 전략 모두 성능 향상이 있지만, 일반적으로 truncated matrix entropy가 더 우수한 결과를 보인다.
- 64K 컨텍스트처럼 극도로 드문(sparse) 환경에서는 truncated matrix entropy에서 r=1을 사용하는 것이 가장 우수한 성능을 보였다.
이 설정은 사실상 스펙트럴 노름(즉, σmax(Σ)\sigma_{\text{max}}(\Sigma))과 동등하게 해석될 수 있으며,
환경이 더 sparse할수록 특이값 분포가 더욱 날카롭고 집중되는 경향이 강해진다는 것을 시사한다.
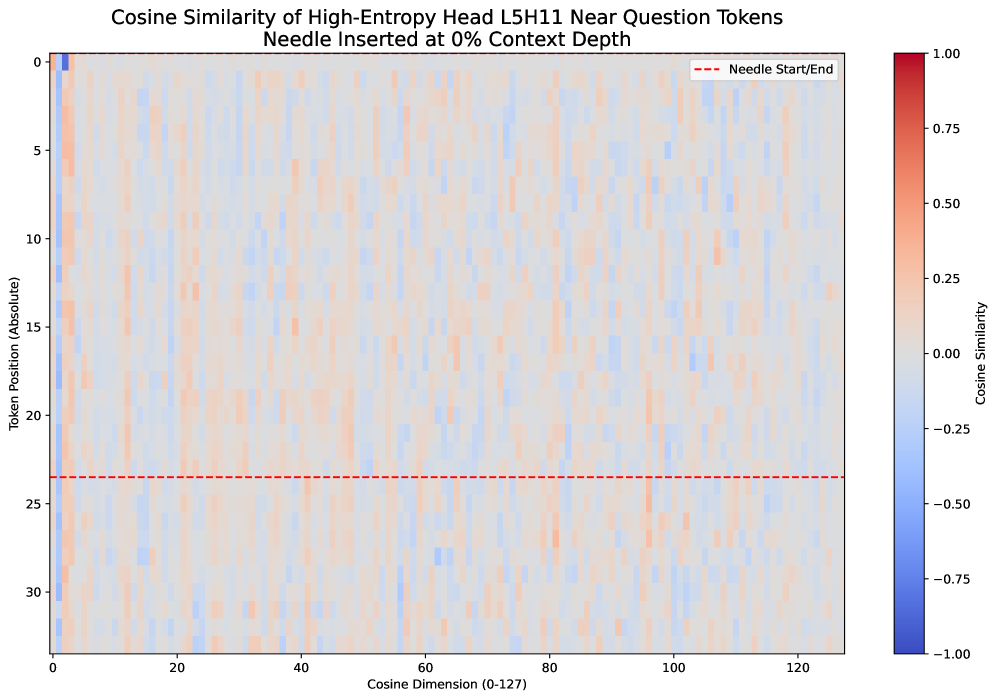
그림 3: 높은 matrix entropy를 갖는 헤드 예시 (Layer 5, Head 11)

그림 4: 낮은 matrix entropy를 갖는 헤드 예시 (Layer 1, Head 2)
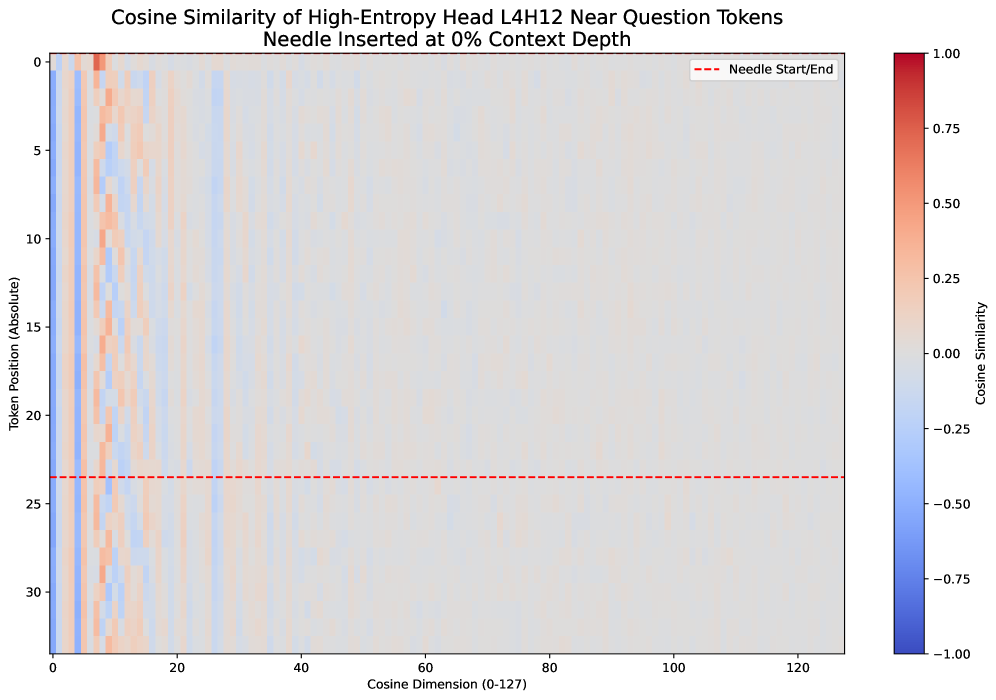
그림 5: 높은 truncated matrix entropy 예시 (Layer 4, Head 12)
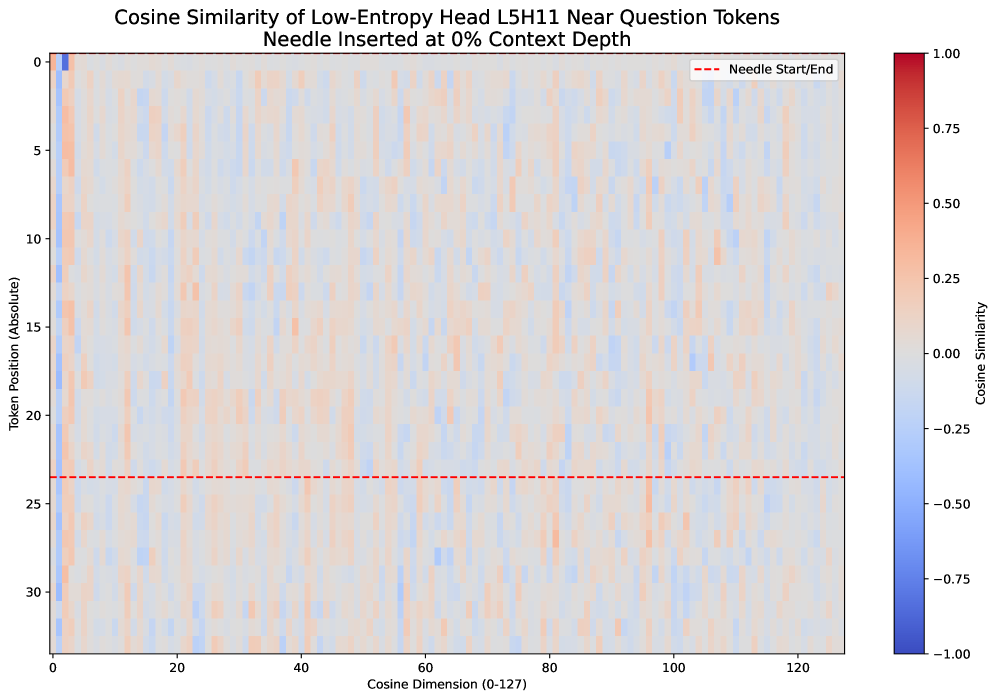
그림 6: 낮은 truncated matrix entropy 예시 (Layer 5, Head 11)
✓ 쉬운 버전 요약 (5.2 실험 결과)
실험을 두 가지 환경에서 테스트했다.
- Original: 정상적인 긴 문서
- Noisy: 중요한 정보 근처에 방해되는 토큰(Attention Sink)을 일부러 넣어 혼란을 준 환경
결과는 다음과 같다:
1️⃣ 방해 토큰을 넣으면 모델이 크게 흔들린다.
중요한 단서를 못 찾고 엉뚱한 데 집중하는 현상이 발생.
2️⃣ 포지션 인코딩에 가우시안 노이즈를 넣으면 성능이 가장 많이 좋아졌다.
특히 24K 길이 실험에서 최고 성능을 달성.
즉, LLM의 위치 인코딩 누적 패턴이 사실상 가우시안과 비슷하게 동작한다는 것을 뒷받침해준다.
3️⃣ 어떤 헤드를 수정할지 고르는 방식이 매우 중요하다.
- Truncated entropy: 지나치게 특정 위치를 응시하는 헤드 제거
- Vanilla entropy: 너무 분산된 헤드 제거
둘 다 성능은 오르지만, Truncated entropy가 더 안정적으로 잘 됨.
4️⃣ 컨텍스트가 아주 길어질수록(예: 64K) 한 방향으로 치우친 헤드가 더 심해진다.
그래서 단 1개의 주된 특이값만 보는 방식(r = 1)으로 선택하는 것이 가장 효과적이었다.
5.3 Many-Shot In-Context Learning
모델의 Many-Shot In-Context Learning(MICL) 성능은 표 2에 제시되어 있다.
실험은 두 가지 방식으로 수행되었다.
- 테스트 예제가 ICL 예제들 사이에 삽입된 경우
(needle-in-a-haystack 방식) - 테스트 예제를 삽입하지 않은 일반 ICL 방식
이 과제는 단순히 모델이 “건초 더미 속 바늘”을 찾을 수 있는지 평가할 뿐 아니라,
컨텍스트에 포함된 예제들로부터 유사한 추론 패턴을 학습·활용할 수 있는지도 함께 검증한다.
요약하면 다음과 같은 결과를 확인했다.
● 길이의 저주(The Curse of Length)
적절한 길이에서는 MICL이 모델의 추론 능력을 크게 향상시킨다.
하지만 컨텍스트 길이가 16K에 도달하면 모델의 최종 추론 능력이 급격히 떨어진다.
즉, 예제를 더 많이 제공한다고 해서 성능이 계속 좋아지는 것이 아니다.
이는 복잡한 추론 능력이 외삽 가능한 길이에 의해 제약됨을 간접적으로 보여준다.
● 지름길의 저주(The Curse of Shortcut)
테스트 샘플의 예제를 ICL 예시에 그대로 포함시켰다.
그러면 모델이 단순히 정답을 “needle-in-a-haystack 방식으로” 복사해 내서 성능이 올라갈 것으로 예상할 수 있다.
그러나 실제 결과는:
오히려 컨텍스트 길이가 24K와 64K인 경우 전체 성능이 크게 떨어졌다.
즉, 정답을 바로 옆에 보여줘도 성능이 올라가지 않았으며,
이 현상은 긴 컨텍스트 환경에서는 모델이 정답을 활용하는 지름길을 제대로 이용하지 못함을 의미한다.
5.4 Matrix Entropy와 Attention Sink의 관계
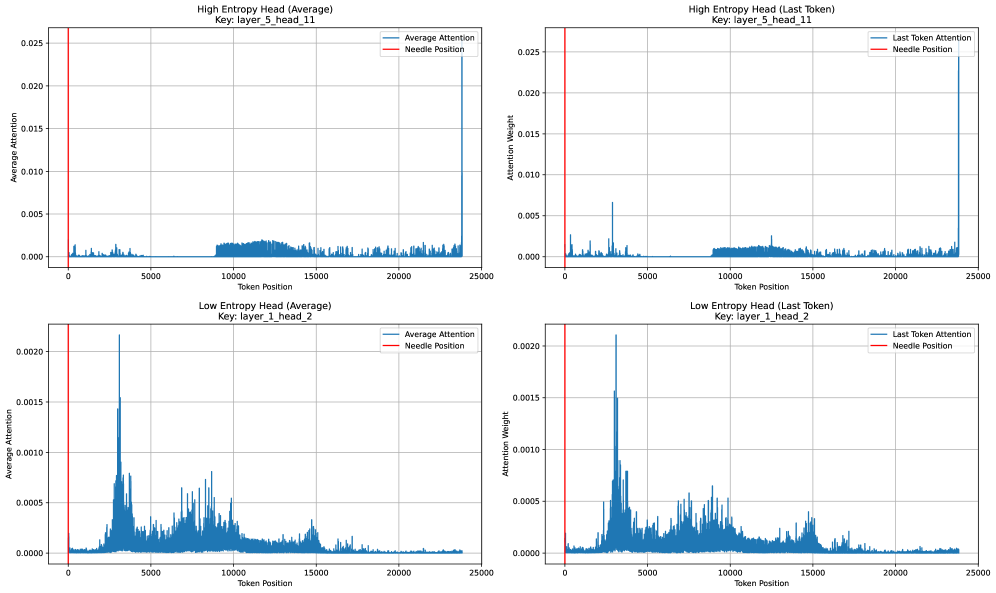
본 절에서는 높은 truncated matrix entropy 기준으로 식별된 어텐션 헤드들의 attention 분포를 직접 시각화한다.
그림 2는 truncated matrix entropy와 attention 분포(특히 attention sink) 사이의 강한 연관성을 명확하게 보여준다.
그림 2(b)로부터 다음과 같은 결론을 내릴 수 있다.
- truncated matrix entropy가 낮은 헤드(low-entropy heads)를 식별했을 때, 해당 헤드들은 심각한 attention sink(최근 토큰에 과도하게 쏠리는 현상)를 보이는 경향이 있다.
- 반면 남아 있는 high-entropy 헤드들은 삽입된 needle(핵심 정보)에 주의를 올바르게 배분한다.
반대로 그림 2(a)에서는 다음과 같은 패턴이 확인된다.
- 전체적으로 matrix entropy가 높게 나타나며, 이는 전반적으로 심각한 attention sink를 의미한다.
- low-entropy 헤드들은 비교적 정상적인 attention 분포를 생성하지만, needle의 올바른 위치를 찾는 데 실패한다.

● Low-rank 특성
엔트로피 기준으로 선택된 헤드들은 명확한 low-rank 경향을 보인다.
그림 4와 그림 6 모두, 해당 헤드가 유지한(low entropy 또는 high truncated entropy) 경우:
- 유사도(색상)가 전체 128차원 중 일부 소수 차원에만 집중되어 있다.
즉, 이 low-rank 헤드는 소수의 차원만으로 외삽(extrapolation) 추론을 수행하며,
이는 긴 문맥에서도 검색/복원 성능이 좋은 retrieval head일수록 일부 핵심 feature만 사용한다는 점을 의미한다.
● 주기성(Periodicity)
그림 6에서 볼 수 있듯, truncated matrix entropy로 선택된 헤드의 유사도 분포는 세로축(토큰 위치) 방향으로 뚜렷한 주기성을 보인다.
반면 vanilla matrix entropy로 선택된 헤드(그림 4)는 이러한 주기적 패턴이 약하다.
이 관찰은 다음을 설명한다:
truncated matrix entropy가 full matrix entropy보다 긴 문맥 외삽 성능이 뛰어난 헤드를 더 정확히 찾아낼 수 있는 이유는,
주기성이 강한 low-rank 구조가 외삽에 유리하기 때문이다.
6 결론
본 연구에서는 Denoising Positional Encoding(DoPE)을 제안하였다. DoPE는 추가 학습이나 파라미터 없이 truncated matrix entropy 분석을 통해 RoPE(Rotary Position Embedding)에서 발생하는 low-rank 아티팩트 문제를 완화하는 방법이다.
노이즈가 많은 헤드를 식별하고 저엔트로피 주파수 대역을 억제함으로써, DoPE는 attention sink 현상을 효과적으로 줄이고 균형 잡힌 positional representation을 회복한다.
긴 컨텍스트 및 noisy 환경에서의 실험 결과, DoPE는 다양한 모델에서 외삽 성능(extrapolation)과 추론 안정성(reasoning stability)을 향상시키는 것으로 확인되었다.
이 연구는 truncated matrix entropy가 positional encoding 개선 및 Transformer의 장문 generalization을 강화하기 위한 간단하지만 이론적 근거가 확실한 방향임을 보여준다.