INT v.s. FP: A Comprehensive Study of Fine-Grained Low-bit Quantization Formats

Modern AI hardware, such as Nvidia's Blackwell architecture, is increasingly embracing low-precision floating-point (FP) formats to handle the pervasive activation outliers in Large Language Models (LLMs). Despite this industry trend, a unified comparison

arxiv.org

초록
최신 AI 하드웨어, 특히 Nvidia의 Blackwell 아키텍처는 대규모 언어 모델(LLM)에서 빈번하게 발생하는 activation outlier 문제를 처리하기 위해 저정밀도 부동소수점(FP) 형식을 적극적으로 채택하고 있다. 그러나 이러한 산업적 흐름에도 불구하고, 다양한 정밀도와 양자화 단위(granularity)에 걸쳐 부동소수점(FP)과 정수(INT) quantization을 체계적으로 비교한 연구는 부족했으며, 이로 인해 알고리즘–하드웨어 공동 설계에 명확한 방향성이 부재한 상태였다. 본 논문은 FP와 INT 형식 간의 트레이드오프를 체계적으로 분석함으로써 이러한 공백을 채우고자 한다.

우리는 중요한 성능 교차점을 발견했다. 즉, 거친(granularity가 큰) 양자화에서는 FP가 우수하지만, 미세한 블록 단위(fine-grained, block-wise)에서는 비교가 훨씬 복잡해진다. 우리의 종합적인 비교에 따르면, 널리 사용되는 8비트 미세 블록 기반 형식(예: 블록 크기 32의 MX)에서는 알고리즘 정확도와 하드웨어 효율성 모두에서 MXINT8이 해당 FP 형식보다 우수함을 확인했다.

반면 4비트 형식에서는 FP(MXFP4, NVFP4 등)가 대체로 정확도 측면에서 우위를 점한다. 그러나 outlier 완화를 위한 Hadamard rotation과 같은 기법을 적용할 경우 NVINT4가 NVFP4를 능가할 수 있음을 우리는 보여준다.

또한, 본 논문은 미세 블록 단위의 저비트 INT 훈련에서 발생하는 gradient bias를 해결하기 위한 대칭적 클리핑(symmetric clipping) 기법을 제안하며, 이를 통해 MXINT8 훈련에서 거의 손실 없는 성능을 달성할 수 있음을 보인다.

이러한 결과는 현재의 하드웨어 개발 방향에 도전한다. 즉, 단일 FP 기반 접근은 최적이 아니며, 특히 MXINT8과 같은 미세 블록 기반 INT 형식이 정확도, 전력 효율, 하드웨어 효율성 측면에서 더 균형 잡힌 선택지임을 강조한다.

[Code]https://github.com/ChenMnZ/INT_vs_FP

GitHub - ChenMnZ/INT_vs_FP: A framework to compare low-bit integer and float-point formats

A framework to compare low-bit integer and float-point formats - ChenMnZ/INT_vs_FP

github.com

1 서론
대규모 언어 모델(LLM)의 확산은 계산량과 메모리 요구량의 급격한 증가와 함께 이루어졌으며 [43], 이로 인해 효율적인 모델 배포를 위해 양자화(quantization)는 필수적인 기술이 되었다. Transformer 아키텍처 기반 LLM을 양자화할 때 가장 큰 난제 중 하나는 활성화(activation) 분포 내에 존재하는 강한 outlier들이다 [38, 12]. 이러한 outlier는 크기는 크지만 빈도는 매우 낮은 값들로, 저정밀도 표현 방식에서는 큰 문제를 야기한다.

이처럼 넓은 동적 범위를 표현해야 하는 어려움 때문에, AI 하드웨어 업계 [31]는 FP8, FP4와 같은 저정밀도 부동소수점(FP) 형식으로 빠르게 이동하고 있다. NVIDIA의 Blackwell 아키텍처 [31]는 이러한 흐름을 잘 보여주는 대표적 사례로, 전통적인 정수(INT) 형식보다 FP 형식이 갖는 더 넓은 동적 범위를 활용해 outlier 문제를 더 안정적으로 처리할 수 있다는 점이 강조되고 있다.

그러나 업계 전반에서 이어지고 있는 이러한 FP 형식 중심의 흐름은 불완전한 이해를 기반으로 하고 있다. FP와 INT의 상대적 장단점은 다양한 양자화 단위(granularity)에 대해 통합된 관점에서 체계적으로 평가된 적이 거의 없다. 기존 연구들 [41, 6, 22]은 대부분 하나의 형식에만 집중하거나, 비교하더라도 per-channel과 같은 거친 단위(coarse granularity)에서만 수행되어, 중요한 질문에 답하지 못하고 있다. 즉, 양자화 단위가 미세해질수록(INT와 FP 사이의 성능·효율 트레이드오프가 어떻게 변화하는가?)라는 핵심 문제가 여전히 밝혀지지 않았다.

현재 outlier 문제 해결을 위해 미세 블록 단위(fine-grained, block-wise) 양자화가 표준 기술로 자리잡고 있는 만큼 [34, 32], 이러한 구조가 수 표현 형식(number format)과 어떻게 상호작용하는지 이해하는 것은 효과적인 알고리즘–하드웨어 공동 설계를 위해 필수적이다.

본 논문에서는 미세 블록 단위(fine-grained) INT 및 FP quantization에 대한 포괄적이고 체계적인 비교를 수행한다. 우리의 분석 결과, 성능 면에서 중요한 “교차 지점(crossover point)”이 존재함을 확인했다. 거친 양자화 단위(coarse-grained)에서는 FP 형식이 확실한 우위를 보이지만, 블록 크기가 작아질수록 INT 형식이 매우 경쟁력 있게 변화하며, 그 효과는 비트 폭(bit width)에 크게 의존한다.

양자화의 단위가 더 미세해질수록 각 블록 내의 지역적(dynamic range)이 크게 감소하며, 이에 따라 INT 형식이 가진 균일 정밀도(uniform precision)가 더욱 효과적으로 작용하게 된다. 이러한 현상은 Microscaling(MX) 형식의 32-element 블록이나 NVIDIA(NV) 형식의 16-element 블록과 같은 현대적인 블록 기반 양자화 방식 전반에서 관찰된다.

정확한 비교를 위해, 우리는 기존 FP 형식(MXFP8, MXFP6, MXFP4, NVFP4)에 대응하는 정수 기반 변형(INT 기반 quantization)을 정의하고 평가한다. 예를 들어 MXINT8, MXINT6, MXINT4, NVINT4 등을 새롭게 도입하여 그 성능을 FP 대응 모델들과 직접 비교한다.

우리의 주요 기여는 다음과 같다:

• INT와 FP 형식 모두에 대해 quantization SNR(QSNR)을 모델링하는 이론적·통계적 프레임워크를 제안한다. 이 프레임워크는 두 형식 간의 성능 트레이드오프를 이론적으로 직접 비교할 수 있게 하며, 성능 교차 지점(crossover point)을 명확히 규명한다.

• MXINT8이 직접 캐스팅(direct-cast) 기반 추론과 저비트(low-bit) 훈련 모두에서 MXFP8을 일관적으로 능가함을 보인다. 또한 Hadamard rotation을 적용할 경우 NVINT4가 NVFP4를 넘어설 수 있음을 실험적으로 입증한다. 특히, 우리는 gradient bias 문제를 해결하는 대칭 클리핑(symmetric clipping) 기법을 새롭게 제안하여 MXINT8 저비트 훈련에서도 거의 손실 없는 성능을 달성한다.

• 하드웨어 비용 분석을 제시하여, 동일한 처리량(throughput) 기준에서 미세 블록 기반 INT 형식이 FP 형식 대비 칩 면적(area)과 에너지 효율(energy efficiency) 측면에서 훨씬 우수함을 보여준다.

• 이러한 결과들을 종합하면, 현재의 FP 중심 하드웨어 설계 흐름이 최적이 아님을 분명히 보여주며, 미세 블록 기반 INT 형식이 정확도와 효율의 균형 측면에서 차세대 AI 가속기에 더 적합한 선택지임을 강하게 제안한다.

2 사전 지식(Preliminaries)
Quantization은 고정밀(high-precision) 텐서 𝐗를 더 낮은 비트 폭(bit-width)으로 변환하는 과정이다. 본 절에서는 저비트 정수(INT) quantization과 부동소수점(FP) quantization을 소개하고, 특히 미세 블록 단위(fine-grained block-wise) 방식을 중심으로 quantization granularity를 설명한다. 또한 기존에 사용되는 다양한 저비트 블록 기반 형식들에 대한 개요를 제공한다.

2.1 저정밀도 정수(Integer) 형식

b비트 정수 양자화는 다음과 같이 정의된다:

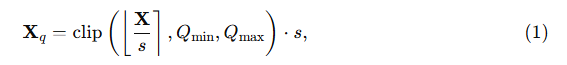
여기서
• s는 텐서 X 를 목표 정수 범위로 정규화하는 스케일(scale) 이고,
• ⌊⋅⌉ 은 가장 가까운 정수로 반올림(round-to-nearest) 을 의미하며,
• X_q는 dequantized된 텐서다.

클리핑(clipping)은 양자화된 값이 정해진 정수 구간 [Q_min⁡,Q_max⁡]안에 있도록 보장한다. 예를 들어, signed b비트 정수의 경우:

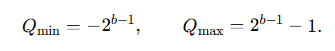
위 구간이 정수 표현 가능한 전체 범위를 정의하게 된다.

2.2 저정밀도 부동소수점(Floating-Point) 형식

부동소수점 표현 방식 [24]은 부호 비트(sign, S), 지수(exponent, E), 가수(mantissa, M)의 세 부분으로 구성된다. 우리는 형식을 E_xM_y로 표기하며, 여기서
• x는 지수 비트 수,
• y는 가수 비트 수를 의미한다.

부호 비트는 값의 부호를 결정하고, 지수는 동적 범위(dynamic range)를, 가수는 정밀도(precision)를 결정한다. 부동소수점 수는 다음과 같이 복원된다:

여기서
• s,e,m은 각각 부동소수점 수의 부호(sign), 지수(exponent), 가수(mantissa) 값을 의미한다.
따라서 C_FP는 해당 저정밀도 부동소수점 형식에서 표현 가능한 값들의 집합이다.

부동소수점 quantization은 다음과 같이 정의된다:

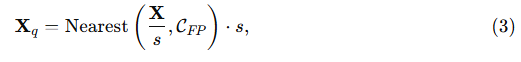
여기서
• Nearest(⋅,CFP)는 정규화된 값을 C_FP 집합에 속한 가장 가까운 부동소수점 값으로 매핑하는 함수이다.

식 (3)은 일반적인 양자화 표현이며, C_FP를 C_INT로 대체하면 정수 기반 quantization이 동일한 형태로 복원된다.

2.3 Quantization Granularity

Quantization granularity는 스케일(scale) 파라미터가 텐서 내에서 어떻게 적용되는지를 정의한다. 일반적으로 granularity가 더 미세할수록 정확도는 향상되지만, 스케일 개수가 증가하기 때문에 연산 및 메모리 오버헤드도 커진다. 대표적인 granularity 선택지들은 다음과 같다:

(i) Per-tensor: 텐서 전체에 대해 하나의 스케일을 사용.
(ii) Per-channel: 특정 축을 기준으로 각 채널마다 하나의 스케일을 사용.
(iii) Block-k: 텐서를 한 차원에서 1×k 블록으로 나누고, 각 블록마다 고유한 스케일을 사용.

Block quantization은 저정밀도 환경에서 정확도를 향상시키는 핵심 기법이며, 본 논문에서는 주로 block quantization을 중심으로 다룬다.

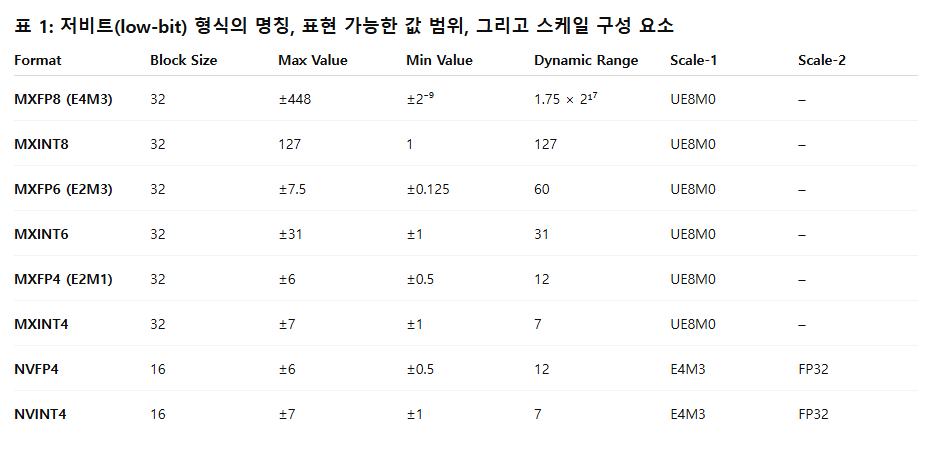
2.4 블록 기반(Block) 양자화 형식

저비트 환경에서 정확도를 향상시키기 위해 OCP [34]는 Microscaling(MX) 형식을 제안했으며, 이는 32개 요소로 구성된 각 블록마다 하나의 공유 UE8M0¹ 스케일을 사용하는 방식이다. 이러한 미세 블록 단위 스케일링은 양자화 오차를 크게 줄여 준다. 최근 NVIDIA의 Blackwell GPU 시리즈 [32]는 MXFP8, MXFP6, MXFP4에 대한 하드웨어 수준 지원을 제공한다.

전통적으로 FP8은 E4M3, E5M2 두 가지 변형을 갖고 있으며, FP6은 E2M3, E3M2 변형을 가진다. 본 논문에서는 선행 연구 [21, 27, 34]와 동일하게, MXFP8에는 E4M3, MXFP6에는 E2M3를 사용한다. 이는 가수 비트(mantissa bit)가 미세 블록 기반 양자화의 성능에 더 중요한 역할을 하기 때문이다.

또한 NVIDIA는 MXFP4를 확장한 NVFP4를 제안했는데, 이는
• 블록 크기를 32에서 16으로 줄이고,
• 스케일 형식을 UE8M0에서 E4M3로 변경했으며,
• 1단계 스케일(E4M3)의 overflow를 방지하기 위해 2단계 per-tensor scale을 도입한 형식이다.

이러한 흐름으로 인해 최신 하드웨어는 저비트 미세 블록 기반 FP 형식을 주로 지원하는 방향으로 발전하고 있다.

저비트 FP 형식과 정수 형식을 공정하게 비교하기 위해, 본 연구에서는 이에 대응하는 정수 기반 변형 또한 정의한다. 즉, MXINT8, MXINT6, MXINT4, NVINT4 네 가지를 도입하여 FP 형식과 직접 비교할 수 있도록 한다. 각 형식의 세부 사양은 표 1에 제시되어 있다.

¹ UE8M0: 지수 8비트, 가수 0비트로 구성된 8비트 unsigned floating-point 형식.

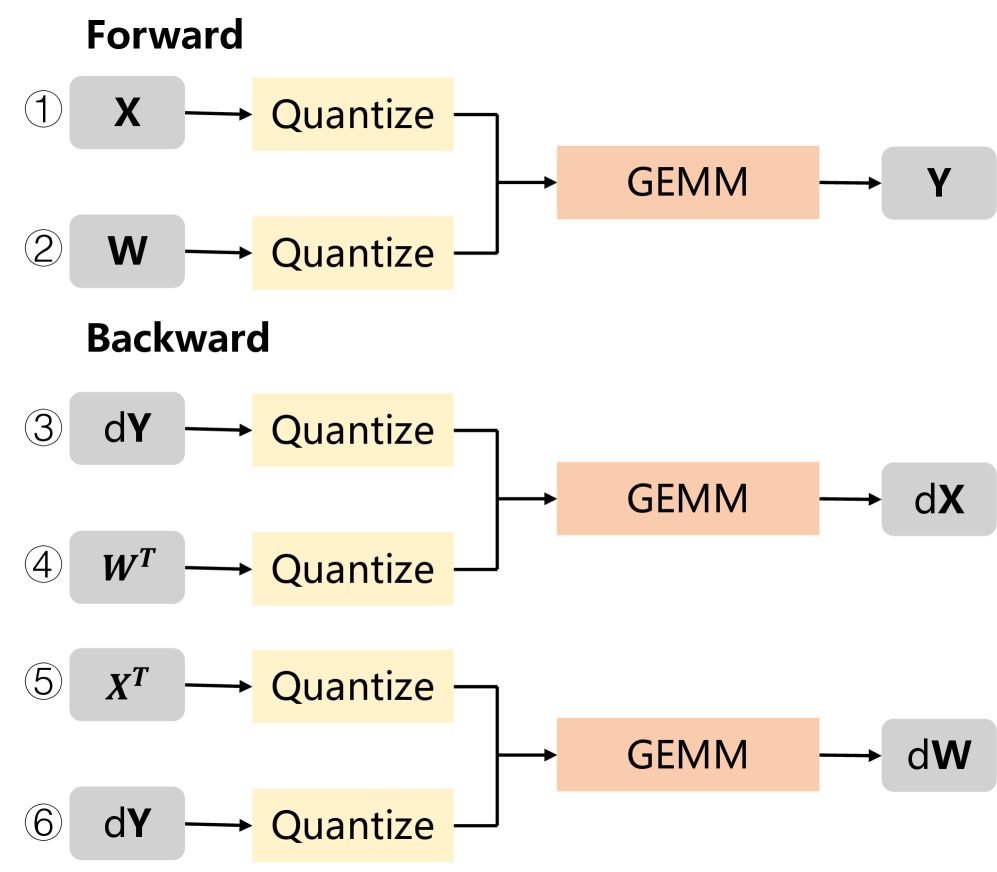
그림 1: 선형 계층(linear layer)에서 저비트 양자화를 적용한 순전파·역전파 연산 흐름.

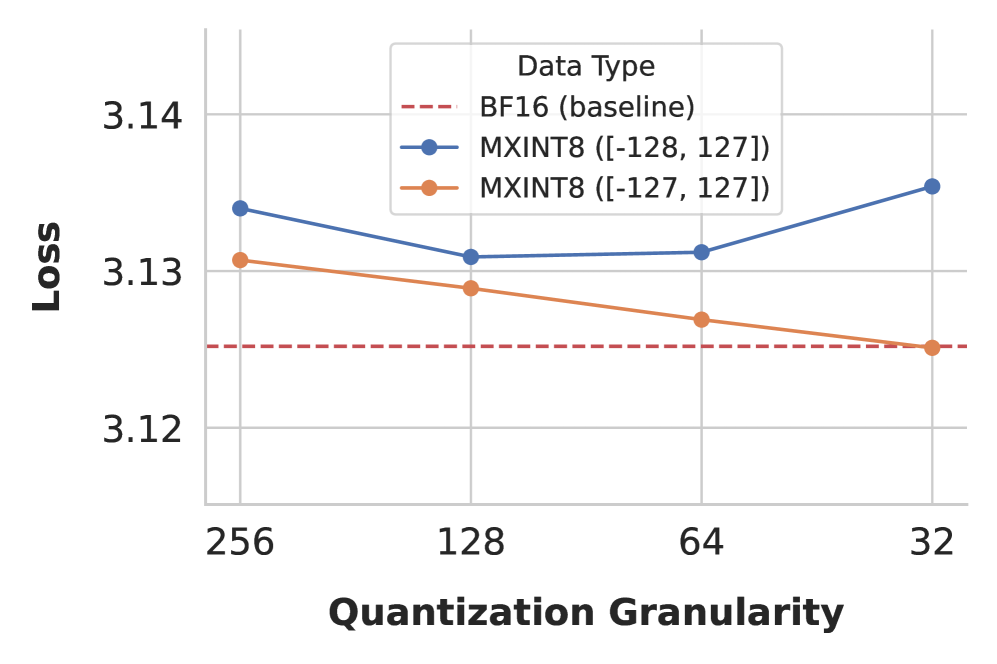
그림 2: 145M 모델을 200억 토큰으로 학습했을 때, INT8의 clipping range가 최종 학습 손실에 미치는 영향. 스케일은 BF16으로 고정하여, 비대칭 정수 표현 공간(asymmetric representation space)이 저비트 훈련에서 야기하는 성능 저하를 강조한다.

3 Quantization Recipe

본 절에서는 다음 내용을 다룬다.
• 3.1절에서는 저비트(low-bit) 환경에서의 추론(inference) 및 훈련(training) 연산 흐름을 설명하고,
• 3.2절에서는 quantization 과정에서 사용되는 스케일(scale) 계산 방법을 상세히 다룬다.

3.1 Quantization Compute Flow

그림 1은 저비트 GEMM을 선형 계층(linear layer)의 순전파와 역전파 과정에 적용하는 예를 보여준다. 고정밀(예: BFloat16) 활성화 값 𝐗와 가중치 𝐖가 주어졌을 때, 양자화된 선형 계층의 순전파는 다음과 같다²:

² 편의를 위해 bias 항은 생략하였다.

역전파에서 dX 와 dW 를 계산하는 과정은 다음과 같다:

여기서 Quantize(·) 는 고정밀 텐서를 저비트 표현으로 변환하는 함수이다.

따라서 하나의 선형 계층에는 총 6개의 양자화 연산이 포함된다:
• 식 (4)의 ① 𝐗, ② 𝐖,
• 식 (5)의 ③ d𝐘, ④ 𝐖ᵀ,
• 식 (6)의 ⑤ 𝐗ᵀ, ⑥ d𝐘ᵀ.

블록 단위(block-wise) quantization은 하드웨어 가속 이점을 얻기 위해 GEMM의 reduction 차원 기준으로 텐서를 양자화해야 한다. 따라서 ①과 ⑤, ②와 ④, ③과 ⑥은 각각 서로 다른 축(axis)을 따라 양자화된다 [21, 11].

이러한 6개의 양자화 연산 각각에 대한 오차 분석은 5.1절에서 별도로 다룬다.

3.2 Quantization Operation

UE8M0 스케일 팩터(scale factor).
식 (1) 및 식 (3)에서 사용되는 스케일 팩터 s는 AbsMax quantizer를 통해 계산된다:

여기서
• AbsMax(X)는 동일한 스케일을 공유하는 값들의 집합에서 절대값 기준 최대값,
• Qmax는 해당 양자화 형식에서 표현 가능한 최대 정수값이다(표 1 참고).

식 (7)은 고정밀 텐서의 가장 큰 크기를 clipping 없이 저정밀 표현 범위의 최대값에 정렬하도록 맵핑하는 방식이다.

OCP [34]는 MX 형식을 위해 고정밀 스케일을 UE8M0 형식으로 변환하는 방식을 제안한다:

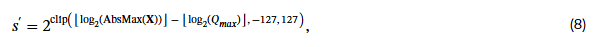
여기서 ⌊⋅⌋는 내림(rounding down) 연산이다.
식 (8)은 고정밀 스케일을 가장 가까운 UE8M0 값 아래쪽으로 내림(round-down) 처리하므로, 추가적인 clipping 오차가 발생한다.

이를 보완하기 위해, 기존 연구 [39, 9, 27]을 따라 우리는 식 (7)에 기반하여 UE8M0 스케일을 올림(round-up) 방식으로 변환한다:

여기서 ⌈⋅⌉은 올림(rounding up)을 의미한다.

이 방식은 UE8M0 스케일을 더 큰 값으로 정렬하여 불필요한 clipping 오차를 방지한다.

대칭적 클리핑(Symmetric Clipping).
부동소수점 형식은 본질적으로 0을 기준으로 대칭적인 표현 범위를 가진다. 그러나 2의 보수(two’s complement)를 사용하는 signed 정수는 한 개의 음수 값이 추가로 존재한다. 즉,
b비트 정수의 경우 표현 범위는 다음과 같다 [32]:

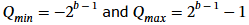
우리는 이러한 비대칭 범위가 추론(inference)에는 거의 영향을 주지 않지만, 그림 2에서 보이듯이 INT8 훈련에서는 지속적인 음수 방향 bias를 유발하여 성능을 저하시킨다는 점을 발견했다. 특히 더 미세한 블록 단위 quantization일수록, 더 많은 값이 독립적인 음수 끝점 Qmin⁡으로 몰리기 때문에 문제가 더욱 심각해진다.

INT8의 경우, BFloat16 계산 정밀도 문제 때문에(자세한 내용은 11.2절 참고), 스케일을

로 설정하더라도, 그룹 내 최소값이 여전히 −128로 매핑되는 현상이 발생할 수 있다.

따라서 우리는 모든 INT quantizer에 대해 완전 대칭 정수 표현 범위를 사용한다. 이는 표 1에서 사용하는 방식과 동일하며 다음과 같다:

이제 본 절에서는 저비트 정수 및 부동소수점 형식을 분석하고, 둘을 비교하기 위한 이론적 프레임워크를 구축한다.
• 4.1절에서는 quantization signal-to-noise ratio(QSNR)에 대한 정리를 유도하며,
• 4.2절에서는 이론적 QSNR을 기반으로 여러 저비트 형식을 비교한다.

4 이론적 프레임워크(Theoretical Framework)

4.1 이론적 QSNR

QSNR 지표(Qualization Signal-to-Noise Ratio).
우리는 서로 다른 quantization 방식에서의 수치적 정확도를 측정하기 위해 QSNR(Quantization Signal-to-Noise Ratio, dB) [11]을 사용한다. QSNR은 원래 신호 𝐗의 파워 대비, 양자화 오차 𝐗 − 𝐗ₚ의 파워 비율을 데시벨(dB) 단위로 표현한 것이다:

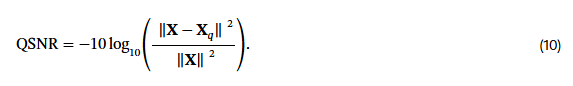
QSNR이 높을수록, 양자화된 벡터가 원래 벡터의 크기와 방향을 더 잘 보존한다는 의미다.

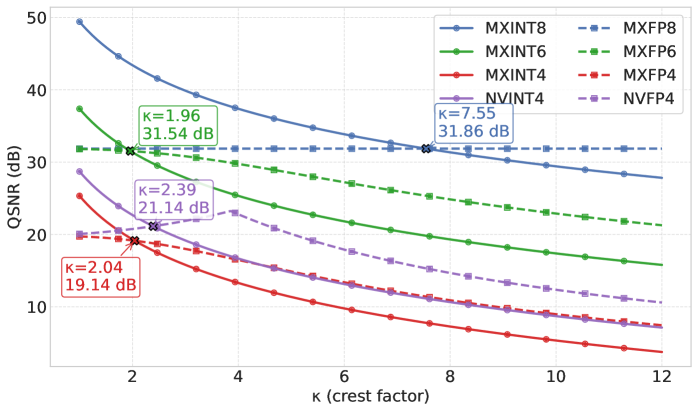
그림 3: 다양한 정수(INT) 및 부동소수점(FP) 형식에 대해 crest factor(κ) 범위 전체에 걸쳐 이론적 QSNR을 비교한 결과.
이 값들은 식 (13)과 식 (14)를 통해 도출되었다. 그림의 박스는 INT와 FP 곡선이 서로 교차하는 지점의 crest factor와 QSNR 값을 나타낸다.

공통 가정(Common assumptions).
우리는 길이가 k인 블록 벡터

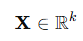
를 고려하며, 각 원소 X_i는 독립 동일 분포

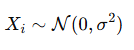
를 따른다고 가정한다.

이때 블록의 RMS(root-mean-square)는 σ\sigma이며, crest factor는 다음과 같이 정의된다:

우리는 블록 단위 absolute-maximum(AbsMax) 스케일링을 사용하며, 스케일은 다음과 같이 정의된다:

여기서
• s는 식 (7)에서 정의된 고정밀 스케일(high-precision scale),
• ρ는 저정밀 스케일 변환에서 발생하는 오버헤드(overhead)를 모델링하는 계수이다.

예를 들어,
• 식 (9)의 UE8M0 스케일은 ρ∈[1,2) 범위 값을 갖는다.
• NV 형식의 E4M3 스케일은 BFloat16 스케일과 유사하므로 ρ=1로 설정한다.

정리 1 (INT QSNR).
b비트 INT quantization에서 QSNR(dB)은 다음과 같다:

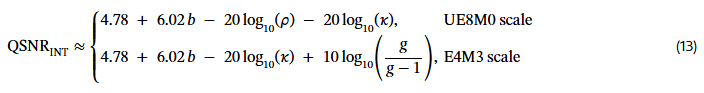
정리 1의 상세한 증명은 9.2절에 제시되어 있다.
여기서
• b는 비트 폭(bit width),
• ρ는 스케일 오버헤드(scale overhead),
• κ는 식 (11)의 crest factor,
• g는 블록 크기(block size)이다.

정리 1의 해석

(i) 비트가 1 증가할 때 QSNR은 약 6.02 dB 증가한다.
(ii) UE8M0 scaling은 최대 20log⁡10(ρ)≤6.02 dB 손실을 유발할 수 있다.
(iii) Crest factor κ가 클수록 QSNR이 감소한다. 블록 크기를 줄이면 보통 κ도 감소하므로 QSNR이 향상된다.
(iv) E4M3 scaling은 오버헤드 ρ\rho가 없으며, 블록 내 최대 오차를 피할 수 있어

만큼 추가적인 QSNR 이득을 제공한다.

✅ 1. QSNR을 직관적으로 이해하기

QSNR(Quantization Signal-to-Noise Ratio)은 말 그대로 신호 대비 양자화 오차의 비율이다.

비유하자면:

원본 신호(𝐗) = 깨끗한 고해상도 사진
양자화된 신호(𝐗_q) = 압축된 사진
QSNR = 압축 후 사진이 얼마나 원본과 비슷한가를 정량적으로 측정한 것

QSNR이 높으면
→ 원본 크기와 방향을 잘 보존
→ 즉, 벡터가 “흔들리는 양”이 작음
→ 모델 정확도가 높게 유지됨

✅ 2. 정리 1이 말하는 INT QSNR 공식의 직관적 의미

INT QSNR:

QSNRINT≈4.78+6.02b−20log⁡10(κ)−(scale overhead)

① 비트 수 b가 1 증가할 때 QSNR이 약 6 dB 증가

비트가 1 증가 → 표현 가능한 값의 정밀도가 2배 증가
→ 오차가 절반으로 감소
→ dB 스케일에서는 6.02 dB 증가

즉,
INT8 → INT6 → INT4로 줄어들수록 QSNR이 크게 감소한다.

② Crest factor κ가 커지면 QSNR이 감소

Crest factor:

κ=max⁡(∣X∣)/σ

즉,
“블록 내에서 가장 큰 값이 RMS 대비 얼마나 큰가”를 측정하는 값.

직관적으로:

만약 블록에 아주 큰 outlier가 1개만 존재한다면
→ 그 큰 값에 맞추어 스케일이 정해짐
→ 나머지 값들이 매우 거칠게 양자화됨
→ QSNR 감소

따라서
Outlier가 많을수록 INT quantization은 성능이 나빠진다.

블록이 작아지면?

32에서 16, 8로 줄어들면
→ Outlier가 있는 위치와 다른 값들이 섞일 확률이 줄어듦
→ Crest factor 감소
→ QSNR 증가
→ fine-grained(block) quantization이 정확도가 더 높은 이유

③ UE8M0을 사용하는 경우 scale overhead ρ 때문에 손실 발생

UE8M0 = exponent만 8비트, mantissa 없음
→ 매우 거친 스케일
→ 실제 필요한 스케일보다 더 큰 값으로 반올림됨
→ 양자화 오차 증가

그래서 다음 항이 생김:

−20log⁡10(ρ)-20 \log_{10}(\rho)

ρ ∈ [1, 2)이기 때문에
최대 약 −6 dB 손실.

즉, MXINT8은 scale 때문에 손해를 보게 됨.

④ E4M3 scale은 overhead 없이 작은 QSNR 이득 존재

NVINT4에서는 스케일이 E4M3 기반(FP 스케일)
→ 스케일 정밀도가 높음
→ scale overhead 없음 (ρ=1)
→ UE8M0보다 유리
→ 다음 항 추가:

+10log⁡10(gg−1)+ 10\log_{10}\left(\frac{g}{g-1} \right)

예: g=16
→ 약 +0.27 dB
g=32
→ 약 +0.13 dB

작지만 일정한 이득이 있음.

✅ 3. QSNR 곡선이 어떻게 생기는가?

QSNR 함수는 κ(crest factor)에 대해 다음과 같은 형태를 가짐:

κ가 커지면
→ QSNR이 직선적으로 감소
→ 기울기 = −20 log(κ)
비트 b가 증가하면
→ 전체 곡선이 위로 평행 이동
scale precision(ρ)이 낮으면
→ 곡선 전체가 아래로 이동

INT vs FP 곡선 비교 시 중요한 포인트

FP는 exponent가 있어 outlier를 다루기 쉬움
→ κ 영향 적음
→ QSNR이 완만하게 감소
INT는 exponent 없음
→ κ에 크게 의존
→ QSNR이 빠르게 떨어짐

그래서 coarse quantization에서는 FP가 항상 강함
하지만, block size를 줄여 κ를 줄이면 INT 성능이 FP에 가까워지고, 때로는 FP를 초과할 수도 있음.

✅ 4. 왜 INT와 FP 곡선이 교차하는가? (크로스오버 포인트)

FP의 강점

exponent로 인해 광범위한 dynamic range 표현 가능
→ κ가 커도 QSNR 유지

FP의 약점

mantissa가 매우 작음 (FP4의 경우 1비트!)
→ 가까운 값 사이 정밀도가 매우 낮음
→ fine-grained quantization에서는 기저 정밀도(mantissa precision)의 부족이 큰 약점

INT의 강점

mantissa 문제가 없음
→ uniform precision
→ block이 작을 때 확실한 이득
→ 8비트 INT는 이미 매우 높은 정밀도 확보

INT의 약점

κ에 약함
→ outlier가 많으면 항상 FP보다 열세

그래서 결과는?

coarse-grained에서 FP > INT
fine-grained(block)에서는 INT가 FP와 경쟁하거나 더 우수
특히 MXINT8은 MXFP8보다 항상 QSNR이 높음
NVINT4는 Hadamard rotation 적용 시 NVFP4보다 우수

→ 논문이 말하는 “성능 교차점(crossover point)”의 핵심 이유가 여기에 있다.

🔥 정리

QSNR 분석은 결국 다음 결론을 줌:

INT는 outlier에 매우 약함
block size를 줄여 crest factor를 억제하면 INT의 단점이 크게 줄어듦
FP는 mantissa가 부족한 경우(fine-grained)는 정밀도가 INT보다 떨어짐
따라서 미세 블록 기반 quantization에서는 INT8이 FP8보다 항상 우세
4비트에서는 FP4가 기본적으로 더 낫지만,
Hadamard rotation으로 outlier를 줄이면 INT4가 FP4를 넘을 수 있음

정리 2 (FP QSNR).
FP quantization에서 QSNR(dB)은 다음과 같다:

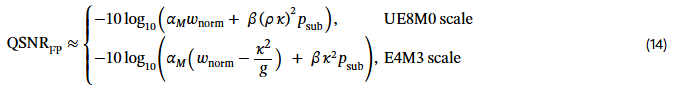
정리 2의 자세한 증명은 9.3절에 제시되어 있다.
식에서 사용된 주요 항은 다음과 같다:

정리 2의 해석(Interpretation)

(i) Mantissa 비트 폭 M이 FP QSNR의 상한을 결정한다

FP는 수 표현 정밀도가 유효 mantissa 비트에 의해 결정되므로, dynamic range가 충분할 때:

QSNR≈13.80+6.02M dB

즉,

mantissa 3비트(E4M3) → 약 31.8 dB
mantissa 1비트(FP4 등) → 약 19.8 dB

이는 block size나 분포의 형태와 거의 무관하다.

(ii) Crest factor κ가 커지면 FP QSNR이 감소한다

Crest factor(식 11):

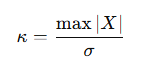
κ가 크면
→ outlier가 많다는 뜻
→ subnormal로 떨어지는 값이 증가
→ p_ 증가
→ QSNR 감소

하지만 FP는 exponent가 있으므로 INT보다 훨씬 완만하게 감소한다.

fine-grained block quantization은 κ를 줄여 FP QSNR을 자연스럽게 증가시키는 효과가 있다.

(iii) E4M3 scaling은 ρ 오버헤드가 없다

UE8M0은 스케일 오버헤드(ρ ≥ 1) 때문에 INT처럼 QSNR 손실이 생기지만,
E4M3 스케일은 그 문제가 없다(ρ=1).

또한 blockwise 스케일링에서

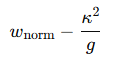
항은 블록 내 최대값 처리 방식이 더 효율적이라는 점을 반영한다.

따라서 E4M3 기반 FP quantization은 UE8M0 기반 FP보다 QSNR이 더 높다.

✅ INT vs FP: 왜 성능 곡선이 교차할까?

INT와 FP 각각의 장단점이 특정 조건에서 서로 반전되기 때문에,
두 곡선은 granularity, bit width, crest factor(κ)에 따라 교차점이 생긴다.

아래에서는 그래프 없이 말로만 들어도 자연스럽게 이해되도록 핵심 개념을 정리한다.

1. INT가 FP보다 유리해지는 조건

특히 MXINT8, NVINT4(+rotation) 같은 변형에서는 FP보다 정밀도가 더 높아질 수 있다.

INT의 강점

mantissa가 필요 없다 → *모든 비트가 정밀도(quantization step)*로 기여
block size를 줄이면 outlier 영향이 크게 줄어듦 → κ 감소
κ가 작아지면 INT QSNR 공식에서 큰 손실 항이 사라짐

INT QSNR 공식 다시 보면:

QSNRINT≈6.02b−20log⁡(κ)\text{QSNR}_{INT} \approx 6.02b - 20\log(\kappa)

여기서 중요한 건:

🔍 블록이 작아지면 κ가 작아진다 → QSNR 크게 상승

즉, block-wise quantization 조건에서는 INT의 가장 큰 약점(κ 민감도)이 거의 사라진다.

🔍 8비트 INT는 이미 매우 높은 해상도

INT8 step = 1
FP8(E4M3) Mantissa = 3 bits → 매우 거침
→ 근처 값끼리 구분이 잘 안 됨
→ fine-grained 환경에서는 mantissa 부족이 큰 단점

따라서 MXINT8이 MXFP8보다 QSNR이 더 높아지는 것
→ mantissa 부족 + κ 감소로 FP가 잃는 영역이 커짐.

2. FP가 INT보다 유리한 조건

특히 MXFP4, NVFP4 같은 4비트 FP에서는 exponent 덕에 INT4보다 더 안정적일 수 있다.

FP의 강점

exponent 덕분에 outlier에 매우 강함
κ 증가에 따른 손실이 INT보다 훨씬 적음
dynamic range가 넓어 clipping 위험이 작음

FP QSNR 공식:

QSNRFP≈6.02M\text{QSNR}_{FP} \approx 6.02M

즉 mantissa가 실제 정밀도.
FP4의 mantissa = 1비트 → 약 19.8 dB 수준.

INT4는 outlier에 매우 취약

INT4 QSNR:

QSNRINT4=6.02\*4−20log⁡(κ)\text{QSNR}_{INT4} = 6.02 \* 4 - 20\log(\kappa)

bit 수는 충분히 높아 보이지만
κ가 조금만 커져도 8~12 dB씩 날아감
→ FP4보다 낮아짐.

그래서 coarse-grained quantization에서는 FP가 절대적으로 우세.

3. 왜 교차점(crossover point)이 생길까?

핵심 이유는 INT는 κ에 민감하고, FP는 mantissa에 민감하기 때문이다.

즉,

✔ coarse-grained → FP가 훨씬 우세

✔ fine-grained(block size 32, 16) → INT가 FP를 앞서기 시작

✔ 특별히 INT8은 거의 항상 FP8보다 우세

✔ 4bit는 rotation 등 테크닉 여부에 따라 순위가 바뀜 (NVINT4 > NVFP4 가능)

4. 그림으로 보면 이렇게 생김

FP8
─────────────── (mantissa 부족으로 평평한 높은 plateau)

INT8
───\────\────\──────── (κ 작아지면 빠르게 상승하여 FP8을 추월)

FP4
─────\────────────── (κ 증가에도 감소폭 작음)

INT4
\──────────────\── (κ 조금만 커져도 빠르게 떨어짐)

→ 그래서 교차 지점이 여러 개 생길 수 있음:

FP8 vs INT8
FP4 vs INT4
NVINT4 vs NVFP4 (rotation 적용 시)
MXFP vs MXINT (block size 따라 다름)

5. 논문 결론 요약

FP는 coarse-grained에서 항상 우세.
INT는 fine-grained(block size 작을수록)에서 더 빠르게 개선되어 FP를 추월.
따라서 block quantization 시대에는 FP 위주 하드웨어 설계가 최적이 아님.
특히 MXINT8은 정확도·전력·면적 모두 MXFP8보다 우수.
4bit는 Hadamard rotation을 적용하면 NVINT4가 NVFP4보다 우세.

4.2 이론적 비교(Theoretical Comparisons)

정리 1의 식 (13)과 정리 2의 식 (14)를 바탕으로, 특정 비트 폭과 목표 분포(즉, κ, crest factor)에 대해 저비트 정수 및 부동소수점 형식의 QSNR을 추정할 수 있다. 특히 UE8M0 스케일의 특성을 반영하기 위해 ρ = 1.5로 설정한다.

그림 3에서 관찰된 주요 비교 결과는 다음과 같다.

• MXINT8 vs. MXFP8

MXFP8은 dynamic range가 넓어 QSNR이 완만하고 안정적으로 변한다.
MXINT8은 κ < 7.55 조건에서 FP8보다 우수하다.

• MXINT6 vs. MXFP6

MXFP6과 MXFP8 모두 mantissa 3비트를 갖기 때문에
→ κ가 작을 때는 동일한 QSNR을 보여준다.
그러나 FP6은 dynamic range가 작아
→ κ가 증가할수록 QSNR이 급격히 감소한다.
MXINT6은 κ < 1.96일 때만 MXFP6을 능가한다.

• MXINT4 vs. MXFP4

MXINT4는 κ < 2.04일 때 MXFP4를 능가한다.

• NVINT4 vs. NVFP4

NVINT4는 κ < 2.39일 때 NVFP4보다 우수하다.

흥미롭게도, NVFP4의 QSNR은 다음 범위에서 오히려 증가하는 현상을 보인다:

κ < 4일 때 NVFP4의 QSNR이 증가

이는 식 (14)의 특성 때문이다.

κ가 커지면 normal 도메인 오차는 감소하지만,
subnormal 도메인 오차는 증가한다.

그리고 작은 κ(κ < 4)에서는 normal 도메인의 영향이 더 크기 때문에, NVFP4의 QSNR이 오히려 증가하는 결과가 나타난다.

5 FP 대 INT (FP v.s. INT)

우리는 저비트 정수(integer) 형식과 부동소수점(floating-point) 형식을 세 가지 관점에서 비교한다.

5.1절에서는 그림 1에 등장하는 여섯 종류의 중간 텐서에 대해 crest factor와 QSNR을 분석하여 텐서 수준 관점에서 비교한다.
5.2절에서는 직접 캐스팅(direct-cast) 기반 추론 성능을 평가하며, 이때는 순전파(forward)만 양자화한다.
5.3절에서는 저비트 훈련(low-bit training) 결과를 제시하며, 순전파와 역전파 모두 양자화하여 학습 성능을 비교한다.

5.1 텐서 단위 분석 (Tensor-wise Analysis)

설정(Setup).
실제 데이터에서 QSNR을 측정하기 위해, WikiText2 [25]의 8개 시퀀스(각 길이 4096)를 Llama-3.1-8B에 입력한다. BFloat16 정밀도로 순전파 및 역전파를 수행한 뒤, 그림 1의 ①–⑥에서 표시된 여섯 유형의 중간 텐서(가중치, 활성화, 기울기)를 수집한다.

이 텐서들을 활용하여

블록 크기별 crest factor,
저비트 형식별 QSNR
을 계산한다.

구체적으로:

QSNR은 텐서 단위로 직접 계산하고,
Crest factor는 block-wise로 계산 후 텐서 차원에서 평균 처리한다.

추가적으로, outlier 억제 기법의 영향력을 평가하기 위해 32 × 32 차원의 랜덤 Hadamard rotation [2]을 적용한 뒤
crest factor 및 QSNR 변화를 측정한다.

(a) Crest factor 대비 QSNR (기본 텐서)

(b) Crest factor 대비 QSNR (Hadamard rotation 적용)

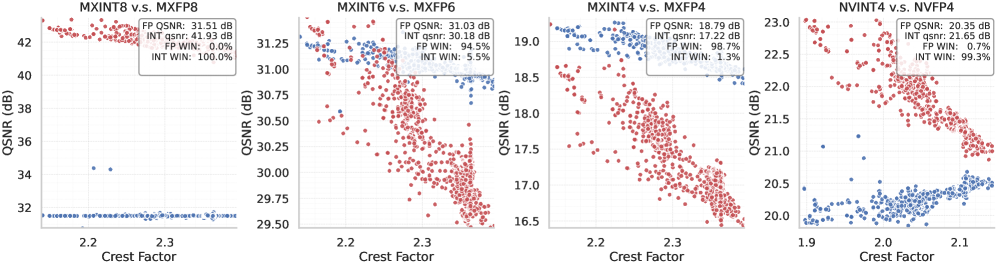
그림 4:
그림 1의 연산 흐름 ①~⑥에서 얻은 총 10,752개 텐서에 대해
crest factor 변화에 따른 실제 QSNR 값을 나타낸 결과.

(a)는 원본 텐서를 양자화한 경우
(b)는 Hadamard rotation을 적용한 뒤 양자화한 경우를 나타낸다.

오른쪽 위 박스에서는

INT와 FP quantization의 평균 QSNR, 두 방식의 승률(win rate)을 각각 보고한다.

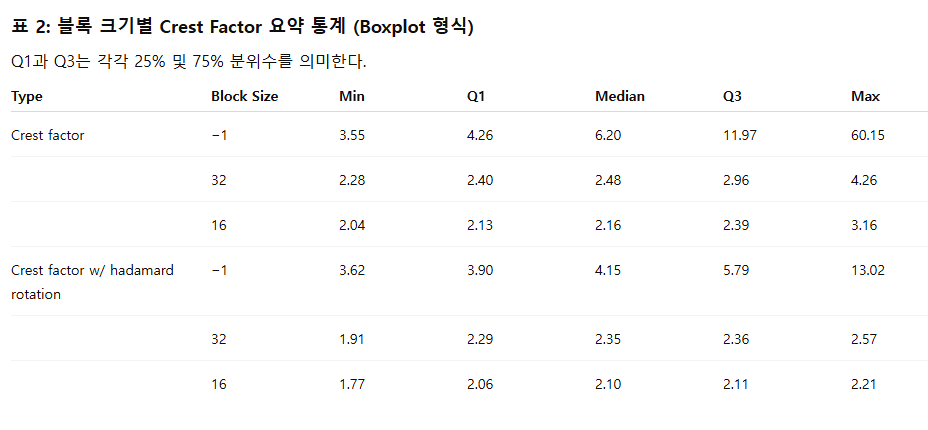
Crest factor 결과

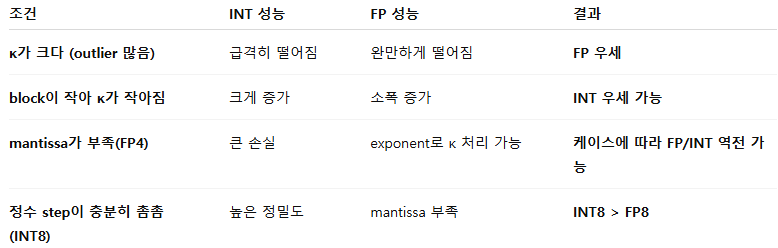
표 2는 crest factor를 boxplot 형태로 요약한 결과이다. 우리는 특히 Q3(75% 분위)에 주목하는데, 이는 전체의 75%에서 나타나는 일반적 최악 사례(typical worst case)를 반영하기 때문이다.

• Channel-wise quantization (block size = −1)

Q3 = 11.97, 이는 그림 3에 나타난 모든 crossover point보다 훨씬 큼
→ coarse granularity에서 FP가 INT보다 대부분의 경우 우세함을 의미한다.

MX-format (block size = 32)

Q3 = 2.96
이는 MXINT8 vs MXFP8 crossover(7.55)보다 훨씬 작음
→ MXINT8이 대부분의 경우 MXFP8을 능가

그러나:

MXINT6 vs MXFP6 crossover = 1.96
MXINT4 vs MXFP4 crossover = 2.04
2.96은 두 임계값보다 큼
→ MXINT6과 MXINT4는 FP 형식을 이기지 못함

• Hadamard rotation 적용 후

MX-format block size 32의 Q3: 2.96 → 2.39로 감소
- 2.39 < 7.55 → MXINT8 여전히 FP8보다 우세
- 2.39 > 1.96, 2.04 → MXINT6, MXINT4는 여전히 FP에 뒤처짐

• NV-format (block size = 16)

Q3 = 2.39
- 이는 NVINT4 vs NVFP4 crossover = 2.39와 동일
Hadamard rotation 후 Q3 = 2.11
→ 2.11 < 2.39
→ Rotation 이후 NVINT4가 NVFP4보다 우세

Crest factor vs QSNR 결과

그림 4는 crest factor 변화에 따른 QSNR 측정값이다.
경향은 Sec. 4의 이론(정리 1–2) 및 위의 crest factor 분석과 잘 일치한다.

• MXINT8 vs MXFP8

MXFP8 QSNR은 dynamic range가 크기 때문에 거의 일정하며, 값은 31.50 dB
MXINT8의 평균 QSNR은 40.35 dB
→ MXINT8이 MXFP8보다 크게 우수

• MXINT6 vs MXFP6 / MXINT4 vs MXFP4

rotation 적용 여부와 관계없이
→ MXINT6과 MXINT4는 항상 FP6 및 FP4보다 뒤처짐

• NVINT4 vs NVFP4

Rotation 이전

NVINT4 승률: 64.3%
NVINT4 평균 QSNR: 20.55 dB
NVFP4 평균 QSNR: 20.60 dB

→ 승률은 높지만, 평균 QSNR은 NVFP4가 소폭 우세
→ 이유: crest factor가 증가할수록 NVINT4 QSNR 감소 속도가 더 빠름

Rotation 이후

NVINT4 평균 QSNR: 21.65 dB → 큰 증가
NVFP4 평균 QSNR: 20.35 dB → 감소

→ Rotation 이후 NVINT4가 NVFP4를 확실히 능가

NVFP4가 감소하는 이유:

Rotation은 crest factor를 감소시킴
그림 3에 따르면 FP4(NVFP4)는 κ < 4 영역에서 κ가 증가할수록 QSNR이 증가
따라서 κ가 감소하면 QSNR이 오히려 감소
→ Rotation 후 NVFP4 QSNR이 낮아지는 것과 정확히 일치

Hadamard rotation은 LLM 양자화에서 outlier를 제거하기 위해 널리 사용되는 정교한 선형 변환이며,
정식 명칭은 Hadamard Transform + 랜덤 부호(random sign) 조합이다.

5.2 Direct-Cast Inference

정밀도(Precisions).

추론에서는 표 1의 다음 형식들을 비교한다:

MXFP8, MXINT8
MXFP6, MXINT6
MXFP4, MXINT4
NVFP4, NVINT4

우리는 사전학습된 BFloat16 모델로부터 direct-cast inference를 수행하며, 순전파의 모든 GEMM 연산을 양자화한다.

모델(Models).

Dense 및 MoE(Mixture-of-Experts) 구조를 모두 포함한 총 12개 LLM을 평가한다.
매개변수 크기는 0.6B부터 235B까지 다양하다:

Qwen3: 0.6B / 1.7B / 4B / 8B / 14B / 32B / 30B-A3B / 235B-A22B [42]
Llama-3.1: 8B, 70B
Llama-3.2: 1B, 3B [13]

또한 Random Hadamard Rotation을 적용하여

Xᴿ,
Rᵀ W
를 양자화한다.
여기서 R은
MX 형식에서는 32×32,
NV 형식에서는 16×16
크기의 랜덤 Hadamard 행렬이다.
공식 오픈소스 링크는 11장에서 제공한다.

평가 지표(Metrics).

정수(INT)와 부동소수점(FP) 저비트 형식을 동일 조건에서 비교하는 것이 목적이므로, 절대 정확도보다는 상대적 성능 순위(ranking)가 더 유의미하다.

기존 연구 [14]에 따르면, 압축 모델은 단순 정확도만으로는 행동 변화(behavior shift)를 감추는 문제가 있어, 정확도 지표만으로는 충분하지 않다.

따라서 우리는 다음을 평가 지표로 사용한다:

✔ BFloat16 모델 대비 KL divergence(WikiText2 [25])

추론 시 softmax 분포의 상위 25개(logits top-25)에 대해 KL divergence를 계산하여 노이즈를 줄인다.

결과(Results).

표 3은 FP와 INT 형식 간 direct-cast inference 비교 요약이다.

Rotation 없이(Original):

MXINT8 → 12개 모델 모두에서 MXFP8보다 우수
MXINT6, MXINT4, NVINT4는 모두 FP6/FP4/NVFP4보다 낮은 성능
NVINT4와 NVFP4는 평균 QSNR이 비슷했지만
→ crest factor가 큰 경우 INT가 더 취약해
→ NVINT4의 패배가 더 잦음

Random Hadamard Rotation 적용 시 (w/ RHT):

MXINT8 → 12개 전부 승
NVINT4 → 12개 전부 승
(rotation이 outlier를 억제해 INT4 성능이 크게 향상)
MXINT6 → 12개 중 1개 승
MXINT4 → 12개 모두 패

이는 Sec. 5.1의 텐서 분석 결과와 정확히 일치한다.

5.3 Training

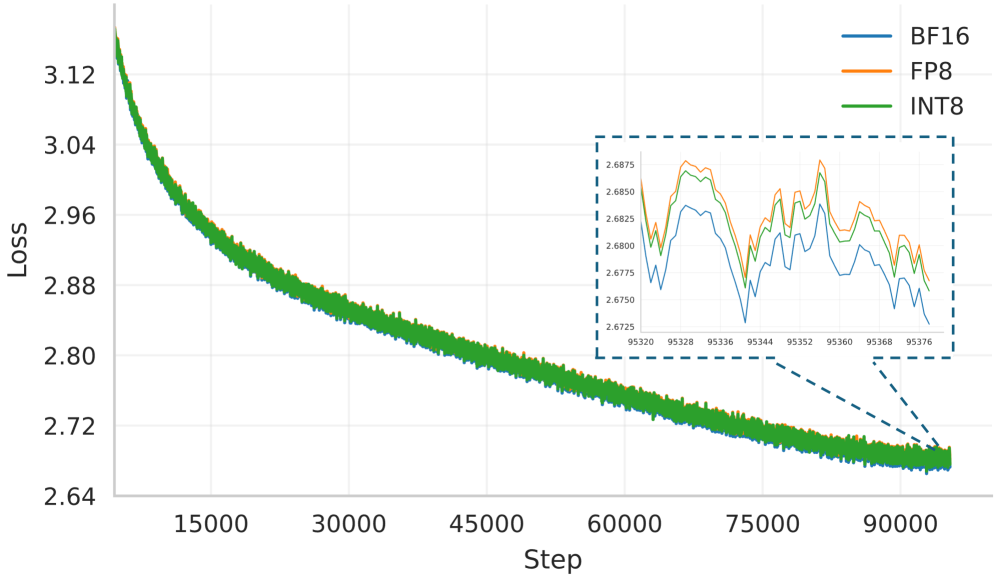
그림 5: Llama-1B 모델을 1,000억(100B) 토큰으로 학습할 때, BF16 / MXFP8 / MXINT8 세 가지 정밀도에서의 학습 손실(loss) 곡선 비교. 지수 이동 평균(EMA, 계수 0.9)으로 스무딩된 결과이다.

정밀도(Precisions).

훈련에서는 거의 손실 없는(low-loss) 저비트 훈련이 실제적으로 중요하다. 따라서 본 연구에서는 8비트 설정에 집중하고, 이전에 여러 연구 [27, 21]에서 FP8 훈련이 거의 손실이 없음을 보여준 바 있으므로, MXINT8과 MXFP8을 비교한다.

모델 및 데이터셋(Models and datasets).

1B 및 3B 규모의 Llama3 스타일 모델을 학습한다.
OLMo2-Mix-1124 [33] 사전학습용 데이터셋 사용
학습 토큰 수:
- 1B 모델: 100B tokens
- 3B 모델: 200B tokens

모델 구조와 학습 하이퍼파라미터는 11장에서 상세히 설명된다.

평가지표(Metrics).

두 가지 지표로 훈련 성능을 평가한다:

훈련 손실(training loss)
- EMA 계수 0.9로 smoothing 처리
태스크 정확도(task accuracy)
- 모든 정확도는 lm_eval [17], 5-shot 평가로 계산
- 제출 지표:
  - WinoGrande → acc
  - HellaSwag / ARC-Challenge / ARC-Easy / PIQA / OpenBookQA → acc_norm

결과(Results).

그림 5 학습 곡선 결과

MXFP8과 MXINT8의 loss 곡선은 BF16과 거의 완전히 겹침
확대 그래프에서 보면 MXINT8의 loss가 MXFP8보다 약 0.001 낮음
→ 지속적으로 MXINT8이 MXFP8을 앞섬

표 4: 저비트 훈련 비교 결과

(HS = HellaSwag, OB = OpenBookQA, WG = WinoGrande)

MXINT8은 BF16과 거의 동일한 평균 정확도를 달성
일부 태스크에서는 MXINT8이 BF16보다 더 높게 나오기도 함
MXFP8과 비교해도 거의 동일하거나 소폭 우위

즉,

✔ MXINT8은 거의 손실 없는(low-loss) 저비트 훈련이 가능함

✔ FP8만이 저비트 훈련의 유일한 해답이라는 기존 관점(선행연구)을 뒤집음

정리하면:

INT 기반 포맷(MXINT8, NVINT4)은 FP 포맷보다
- 에너지 효율이 훨씬 높고
- 칩 면적도 더 적게 필요하며
- 처리량은 동일

→ 하드웨어 측면에서도 INT가 FP보다 훨씬 유리함을 의미

6 하드웨어 비용 분석 (Hardware Cost Analysis)

10장에서 제시한 하드웨어 모델을 기반으로, MX 형식을 지원하는 행렬 곱 연산 유닛(MMU: Matrix-Multiply Unit)의 에너지 및 칩 면적(area) 비용을 평가한다. 표 5에서 볼 수 있듯이, MXINT8과 NVINT4는 각각 MXFP8과 NVFP4 대비 37% 및 38%의 에너지 절감 효과를 보인다.

또한 혼합형 포맷(mixed-format) 구성도 평가한다.
NVIDIA Blackwell GPU [32]를 참조하여,

8-bit과 4-bit 데이터 타입을 모두 지원하고
통신 대역폭을 맞추기 위해 8-bit 대비 4-bit 처리량을 1:2로 설정한 칩 구성을 분석하였다.

표 5에 따르면, “MXINT8+NVINT4” 구성은 “MXFP8+NVFP4” 대비 약 34% 면적 절감을 추가로 달성한다.
이는 INT 파이프라인에서 회로 재사용(circuit reuse)이 FP보다 훨씬 단순하기 때문이다(표 7 참고).

결론적으로, 동일한 처리량(throughput)을 가정했을 때, 저비트 정수(INT) 형식이 저비트 부동소수점(FP) 형식보다 훨씬 더 하드웨어 효율적임을 확인할 수 있다.

7 결론 (Conclusion)

본 연구는 정수(INT)와 부동소수점(FP) quantization 사이의 중요하고도 미묘한 트레이드오프를 포괄적으로 분석하였다.

핵심 발견은 다음과 같다:

FP 형식은 coarse-grained 양자화에서는 효과적이지만,
fine-grained 양자화에서는 MXINT8이 정확도와 하드웨어 효율성 모두에서 MXFP8을 안정적으로 상회한다.
4-bit 형식(MXFP4, NVFP4)에서는 FP가 정확도 면에서 우세한 경향이 있지만,
랜덤 Hadamard rotation을 적용하면 NVINT4가 NVFP4를 능가할 수 있음을 보였다.

이 결과는 FP 중심으로 치우친 현재의 하드웨어 로드맵(Blackwell 등)에 의문을 제기한다.
따라서 우리는 학계와 산업계가 fine-grained INT 형식 중심의 알고리즘–하드웨어 공동 설계(co-design) 방향으로 재조정할 것을 제안한다.

이러한 전환이 향후 AI 가속기의 성능·전력·효율을 모두 개선하는 올바른 전략임을 본 연구는 명확히 보여준다.

Outlines

• 8장에서는 관련 연구를 소개한다.
• 9장에서는 INT 및 FP QSNR 추정과 관련된 정리 1 및 정리 2의 증명을 상세히 다룬다.
• 10장에서는 하드웨어 비용 추정 모델을 제시한다.
• 11장에서는 사용된 모델과 ablation 실험의 추가 세부 내용을 제공하며, 본문에 제시된 그림들에 대응하는 수치 결과를 보고한다.

8 관련 연구 (Related Work)

Quantization Algorithms.

양자화 기법은 크게 두 가지 범주로 나뉜다.

PTQ (Post-Training Quantization)
20,15,36,41
훈련이 끝난 모델을 양자화하는 방식으로, 주로 추론 속도를 높이는 데 사용된다.
QAT (Quantization-Aware Training)
7,23
훈련 과정에서 양자화를 모사하여 정확도 저하를 줄이는 방식.

또한, 저비트 훈련(low-bit training) 27,39,9은 훈련과 추론을 모두 가속화할 수 있다.

여러 연구는 저비트 양자화에 대한 scaling law 18 및 low-bit quantization의 이론적 이해 5,8,16,19도 다루고 있다.

그러나 대부분의 기존 연구는

하나의 low-bit 형식(INT 또는 FP)에만 초점을 두거나
두 형식을 직접 비교하지 않는다.

또한 45는 PTQ 환경에서 모델의 각 부분에 정수 또는 부동소수점 형식을 혼합해 적용하는 mixed-format quantization을 연구하였다.

Hardware.

기존의 많은 AI 가속기 29,30는 미세 단위(fine-grained) quantization을 하드웨어 수준에서 직접 지원하지 않기 때문에,outlier 38 존재 시 per-channel quantization을 사용해야 하는 알고리즘 41,641, 6들이 어려움을 겪었다.

최근 들어 OCP 34는

블록 크기 32
per-block scaling
을 조합한 Microscaling (MX) 데이터 형식을 제안하여
저비트 양자화 성능을 크게 개선했다.

NVIDIA Blackwell 31은

MXFP8
MXFP4
NVFP4

등을 하드웨어 레벨에서 직접 지원함으로써 fine-grained FP quantization 시대를 열었다.

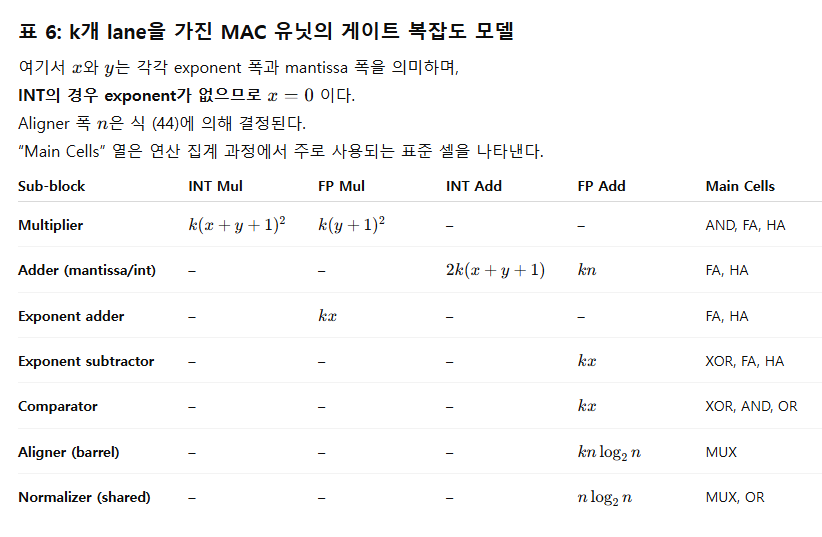
표 7: 동일 lane 수에서의 MAC 유닛 구성 비교 (reuse 방식별)

Note:

No reuse (INT)
- INT8/INT4 기준 가장 높은 에너지 효율
- 하지만 칩 면적 낭비가 가장 큼
INT reuse scheme 1
- int8 lane을 그대로 int4 경로로 사용
- INT4에서 에너지 비용은 약간 증가하지만 면적 비용 감소
INT reuse scheme 2
- 두 개의 int8×(u)int4 lane을 조합해
  int8 lane 또는 int4 lane으로 재구성
- INT4·INT8 모두에서 에너지 비용이 소폭 증가
- 하지만 면적 비용이 가장 낮음 → 가장 공간 효율적
No reuse (FP)
- FP8·FP4 기준 가장 높은 에너지 효율
- 하지만 칩 면적 낭비가 가장 큼
FP reuse scheme
- fp8 lane을 fp4 path로 직접 재사용
  (8비트 입력을 S_00XX_X00 형태로 설정)
- FP4에서 에너지 비용 약간 증가
- 하지만 면적 비용은 감소

우리는 표 5의 면적 비용 평가를 위해

INT reuse scheme 2
FP reuse scheme

을 채택하였다.

10 하드웨어 비용 모델링 (Hardware Cost Modeling)

범위 및 가정(Scope and assumptions)

우리는 저정밀도(low-precision) 형식을 사용하는 GEMM 엔진의 **칩 면적(area)**과 **에너지(energy)**를 추정하기 위한 게이트 레벨(gate-level) 모델을 설계한다.
저비트 GEMM 엔진은 다음 네 가지 구성 요소로 이루어진다:

Quantizer
MAC(Multiply-and-Accumulate) unit
Dequantizer
FP32 accumulator

본 모델은 MAC, 공유 FP32 accumulator, dequantizer만을 비용 계산에 포함한다.
Quantizer는 비용 계산에서 제외된다.

MX/NV 형식에서는 VPU가 quantization을 shift / divide-and-round 방식으로 수행하며,
accumulation 파이프라인에서 dequantization을 다음과 같이 결합(fuse)할 수 있다:

UE8M0 스케일: 8-bit 정수 덧셈 2회
E4M3 스케일: FP 곱셈 2회

이러한 이유로, **곱셈 및 누적(accumulation)**에 의해 발생하는 비용만을 분리해 측정하기 위해 quantizer 블록은 제외한다.

Cell factor는 특별한 언급이 없는 한 TSMC FinFET 표준 셀 라이브러리 기반으로 한다.
또한, 본 모델은 **조합 논리(combinational logic)**만 고려하며,
다음은 포함하지 않는다:

순차 회로(sequential elements)
배치·배선(placement & routing)
인터커넥트(interconnect)

이로써 기술(technology) 차이에 종속되지 않는 **상대적 비교(relativistic comparison)**가 가능하도록 설계한다.

설계 선택: FP32 누적 및 MMU 통합

TPU류 디자인[28]과 유사하게, 고처리량(high-throughput) MMU는
곱셈–누적(chained MAC) 데이터경로와 downstream accumulation을 통합하여 성능 및 에너지 효율을 높인다.

오차 축적 및 확장을 방지하고 확장성(scalability)을 유지하기 위해
우리는 **FP32로 누적(accumulate in FP32)**한다.

동일 명목 비트폭에서
- FP 곱셈기는 INT 곱셈기보다 영역·에너지 효율적
- FP 덧셈기는 INT 덧셈기보다 비용이 크다
  (지수 비교, 지수 감산, mantissa align, normalization 때문)

uniform-alignment 설계[40]를 적용하면, normalization은
모든 kk개 MAC lane에서 하나의 shared normalizer만 사용하도록 줄일 수 있으며,
따라서 normalizer 비용은 kk로 나누어 계산한다.

MAC 유닛 구조

MAC 유닛은 kk-lane array 구조로 모델링된다.

각 lane에는:

1개의 multiplier
lane 전체를 연결하는 multi-input adder tree
FP 형식에서는 mantissa aligner, exponent comparator/subtractor, barrel shifter, normalizer 포함

표 6은 주요 하위 블록(sub-block)의 지배적인 논리 셀 수를 요약한다.

FP multiply: mantissa multiply + exponent add
FP add: exponent compare/subtract + aligner + wide mantissa adder + shared normalizer
INT: 단순화하여 x=0x = 0

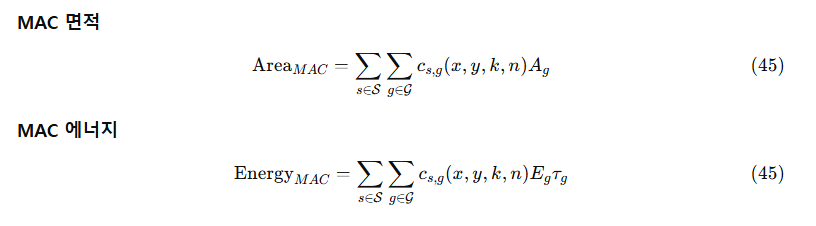
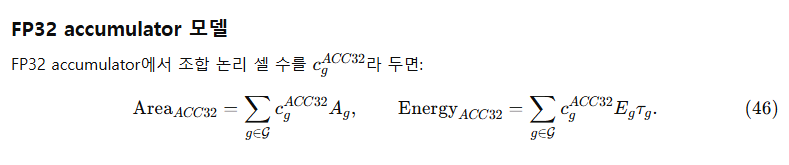
요약(Summary)

이 하드웨어 모델은 다음 세 구성 요소의 비용을 포함한다:

MAC 유닛
Dequantizer
FP32 accumulator

Quantizer는 비용 계산에서 제외된다.

해당 모델은:

형식의 exponent/mantissa 폭 (x,y)(x,y)
(INT의 경우 x=0x=0)
MAC array 크기 kk
aligner 폭 nn (식 44 기반)
표준 셀 라이브러리 기반 기술 cell factor
dequantizer 및 FP32 accumulator 셀 수

를 기반으로 MAC 및 누적 단계의 area/energy를 예측한다.

또한 본 모델은 다음을 포착한다:

MX / NV INT / FP 형식 간 동일 비트폭 대비 하드웨어 비용의 상대적 차이
FP add에서 매우 중요한 **aligner 폭 nn**의 민감도
여러 lane을 공유하는 normalizer, dequantizer, FP32 accumulator의 공유 구조 효과

11 재현을 위한 추가 세부사항 (More Details for Reproduction)

11.1 사용한 모델들 (Used Models)

추론 평가용 모델.
Direct-cast inference에서 평가한 공개(open-sourced) 모델들의 HuggingFace ID를 표 8에 정리하여 재현성을 높였다.
모델 선택 시 다음 기준을 따른다.

먼저, 해당 크기의 base 모델이 오픈소스로 제공되는 경우, SFT 되지 않은 base 모델을 우선 선택한다.
특정 파라미터 규모에 대해 base 모델이 공개되어 있지 않다면, SFT가 적용된 공개 모델 중 하나를 선택한다.

학습 평가용 모델.
실험에서는 널리 사용되는 Llama-3 스타일 모델[13]을 채택했다.
Llama-3 스타일 모델은

self-attention 모듈에 Group Query Attention (GQA)[1],
feed-forward 모듈에 SwiGLU[37]

를 사용한다.
표 9는 실험에 사용된 모델의 상세 아키텍처 설정과 학습 하이퍼파라미터를 보여준다.

11.2 대칭 정수 표현(symmetric integer representation)의 필요성

표 10은 INT8 양자화에서 표현 범위(클리핑 범위)에 대한 ablation 실험 결과를 보여준다.
우리는 표현 범위의 비대칭성(asymmetry)이 INT8 훈련 loss를 일관되게 악화시킨다는 사실을 발견했다.

BFloat16 스케일 팩터를 사용하는 경우,
비대칭 표현 범위는 block size 32인 양자화가 block size 256보다 오히려 더 나빠지는 현상을 만든다.
그 이유는 다음과 같다:
- INT8 양자화에서 각 블록 내 최소값만이 128로 양자화될 가능성이 있다.
- 블록 크기가 작을수록 블록의 개수가 많아지고, 그만큼 극단값이 -128에 매핑될 기회가 많아진다.
UE8M0 스케일 팩터의 경우에도 비대칭 양자화는 성능 저하를 야기하지만,
그 정도는 BFloat16 스케일에 비해 덜 심각하다.
이는 UE8M0 스케일 팩터가 BFloat16 스케일보다 항상 크거나 같기 때문에
더 적은 고정밀 값들이 Qmin⁡Q_{\min}(최소 정수 표현값)으로 매핑되기 때문이다.

이 실험들은 정수 양자화에서 대칭 표현 공간(symmetric representation space)이 필수적임을 보여준다.

수치 안정성 분석.
우리는 Algorithm 1을 통해 서로 다른 부동소수점 정밀도에서의 양자화 매핑 수치 안정성을 분석했다.

표 11에서 보이듯이, BFloat16 정밀도에서는 전체 값의 16.82%가 -128로 매핑된다.
이는 스케일 팩터 s를 이론적으로는 127에 매핑되도록 설계했음에도 불구하고 발생하는 현상이다.

요약하면:

BFloat16 (그리고 덜하지만 float16)의 **정밀도 부족(lack of precision)**으로 인해
스케일링 단계에서 오버플로우가 발생할 수 있으며,
그 결과 값들이 의도한 정수 범위를 벗어나서(-128 등으로) 잘못 매핑될 수 있다.
이는 저정밀 부동소수점 형식을 사용해 양자화 스케일 계산을 수행할 때의 치명적인 함정을 잘 보여준다.
특히, 강제 대칭 클리핑(forced symmetric clipping) 단계가
정수 양자화의 정확성과 안정성을 보장하는 데 필수적임을 강하게 시사한다.

11.3 상세 결과 (Detailed Results)

이 절에서는 실험의 상세 수치들을 제시한다:

표 12, 표 13: 표 3에 대응하는 KL divergence 결과 (값이 낮을수록 좋음)
표 14, 표 15: perplexity 결과
→ KL divergence와 perplexity 간 관계를 이해하기 위한 보조 지표이며, 대부분의 경우 일관된 경향을 보인다.

표 12: Qwen3 모델들에 대한 KL divergence (낮을수록 좋음)

Direct-cast inference에서 다양한 저비트 형식에 대한 결과.
모든 KL 값은 토큰 평균에 10610^6을 곱한 값이다.

(원문의 표를 그대로 사용하되, 의미는 다음과 같다)

위쪽 블록: Qwen-3 (원본, rotation 없음)
아래쪽 블록: Qwen-3 (random Hadamard rotation 적용)

각 행:

MXINT8, MXFP8, MXINT6, MXFP6, MXINT4, MXFP4, NVINT4, NVFP4
각 열:
0.6B, 1.7B, 4B, 8B, 14B, 32B, 30B-A3B, 235B-A22B

표 13: Llama-3 계열 모델에 대한 KL divergence (낮을수록 좋음)

Direct-cast inference에서 다양한 저비트 형식에 대한 결과.
역시 모든 KL 값은 토큰 평균에 10610^6을 곱한 값이다.

위쪽 블록: Llama (rotation 없음)
아래쪽 블록: Llama (random Hadamard rotation 적용)

각 열:

3.2-1B, 3.2-3B, 3.1-8B, 3.1-70B
각 행:
MXINT8, MXFP8, MXINT6, MXFP6, MXINT4, MXFP4, NVINT4, NVFP4

표 14: Qwen3 모델들의 WikiText2 perplexity (낮을수록 좋음)
Direct-cast inference에서 다양한 저비트 형식에 대한 perplexity 결과.

첫 블록: BF16, MXINT8, MXFP8, MXINT6, MXFP6, MXINT4, MXFP4, NVINT4, NVFP4
두 번째 블록: random Hadamard rotation 적용 후 동일 형식들

각 열:

0.6B, 1.7B, 4B, 8B, 14B, 32B, 30B-A3B, 235B-A22B

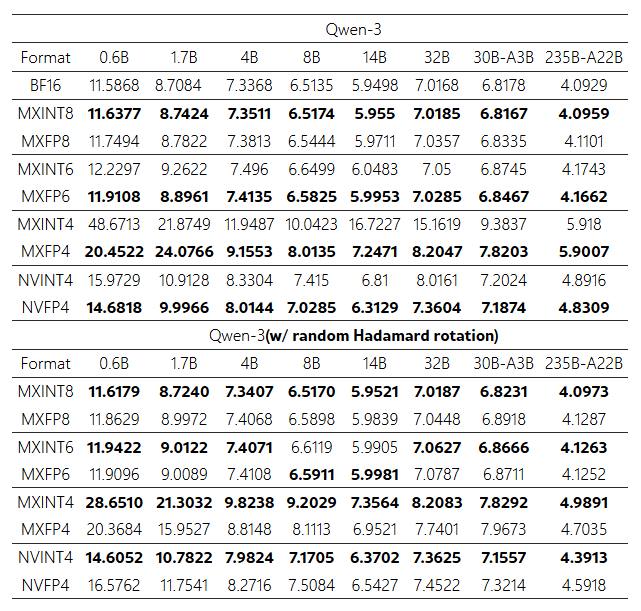
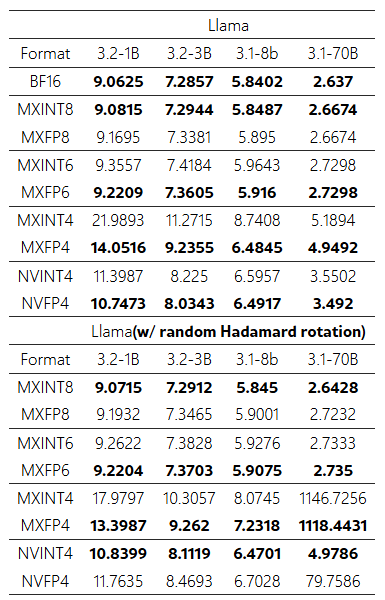
표 15: Llama-3 모델들의 WikiText2 perplexity (낮을수록 좋음)
Direct-cast inference에서 다양한 저비트 형식에 대한 perplexity 결과.

위쪽 블록: Llama (rotation 없음) – BF16 및 여러 저비트 형식
아래쪽 블록: Llama (random Hadamard rotation 적용)

각 열:

3.2-1B, 3.2-3B, 3.1-8B, 3.1-70B

'인공지능' 카테고리의 다른 글

Don't Blind Your VLA: Aligning Visual Representations for OOD Generalization (3)	2025.11.30
DoPE: Denoising Rotary Position Embedding (2)	2025.11.30
Less is More: Recursive Reasoning with Tiny Networks (2)	2025.10.09
Vision-Zero: Scalable VLM Self-Improvement via Strategic Gamified Self-Play (2)	2025.10.06
Polynomial Composition Activations: Unleashing the Dynamics of Large Language Models (6)	2025.08.26