https://arxiv.org/abs/2503.14858?utm_source=pytorchkr&ref=pytorchkr
1000 Layer Networks for Self-Supervised RL: Scaling Depth Can Enable New Goal-Reaching Capabilities
Scaling up self-supervised learning has driven breakthroughs in language and vision, yet comparable progress has remained elusive in reinforcement learning (RL). In this paper, we study building blocks for self-supervised RL that unlock substantial improve
arxiv.org
자기지도 학습(self-supervised learning)의 규모 확장은 언어와 비전 분야에서 큰 돌파구를 이끌어냈지만, 강화학습(RL)에서는 이에 상응하는 발전이 아직 뚜렷하게 나타나지 않았다. 본 논문에서는 자기지도 강화학습의 확장성을 크게 향상시키는 핵심 구성 요소를 분석하며, 특히 네트워크 깊이가 결정적인 요인임을 보여준다. 최근 수년간 대부분의 RL 연구들은 2~5층 정도의 얕은(shallow) 아키텍처에 의존해 왔으나, 우리는 네트워크 깊이를 최대 1024층까지 늘릴 경우 성능이 상당히 향상될 수 있음을 입증한다.
실험은 시연(demonstrations)이나 보상(rewards)이 전혀 주어지지 않는 비지도 목표 조건(unsupervised goal-conditioned) 설정에서 진행되며, 이 환경에서 에이전트는 완전히 처음부터 탐색을 수행하고 주어진 목표에 도달할 확률을 최대화하는 방법을 학습해야 한다. 시뮬레이션 기반 보행 및 조작(manipulation) 태스크에서 평가한 결과, 제안 방식은 자기지도 대비학습 기반 RL(contrastive RL) 알고리즘의 성능을 2배에서 최대 50배까지 향상시키며, 다른 목표 조건 기반 기법들을 능가했다. 모델 깊이를 증가시키는 것은 단순히 성공률을 높이는 데 그치지 않고, 에이전트가 학습하는 행동 양상 자체를 질적으로 변화시키는 것으로 나타났다. 프로젝트 웹페이지와 코드는 다음 링크에서 확인할 수 있다: https://wang-kevin3290.github.io/scaling-crl/.
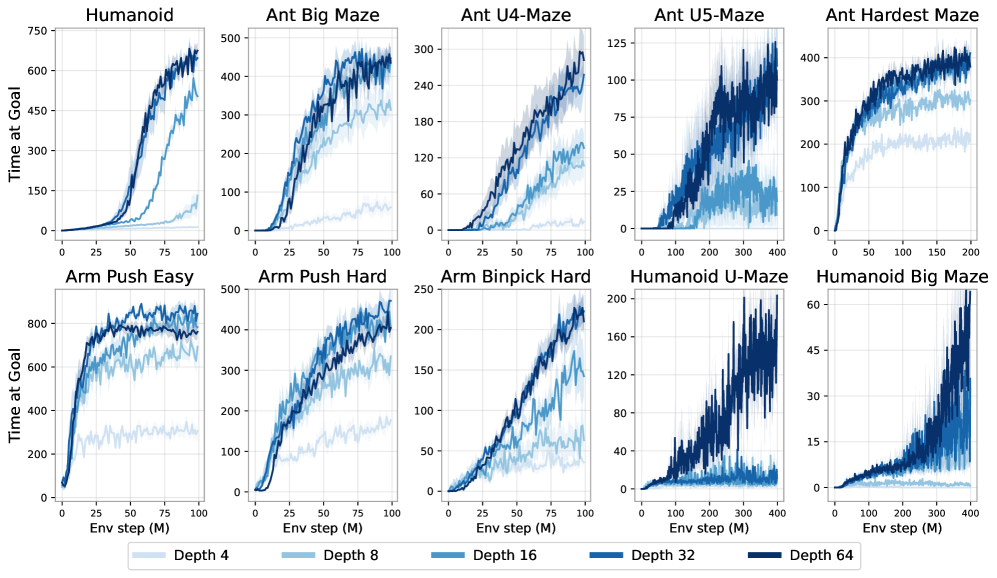
그림 1 설명
네트워크 깊이를 확장하면 다양한 보행, 내비게이션, 조작 태스크 전반에서 성능 향상이 나타난다. Ant Big Maze에서는 깊이 8층, Humanoid U-Maze에서는 깊이 64층과 같이 특정 임계 깊이를 지날 때 성능이 완만하게 증가하는 것이 아니라 급격히 도약하는 양상을 보이는데, 이는 질적으로 구별되는 정책이 그 깊이에서 새롭게 나타나기 때문이다(섹션 4 참고). 성능 향상 폭은 2배에서 Humanoid 기반 태스크에서는 최대 50배까지 도달한다.
1 서론
모델 규모를 확장하는 것은 기계학습의 많은 분야에서 효과적인 전략으로 자리 잡았지만, 강화학습(RL)에서 그 역할과 영향은 아직 명확하지 않다. 상태 기반 RL 태스크에서 사용되는 전형적인 모델 규모는 2~5개의 레이어 수준이다(Raffin et al., 2021; Huang et al., 2022). 반면, 다른 분야에서는 수백 개의 레이어로 구성된 매우 깊은 네트워크를 사용하는 것이 드문 일이 아니다. 예를 들어, Llama 3(Dubey et al., 2024)와 Stable Diffusion 3(Esser et al., 2024)은 모두 수백 개의 레이어를 포함하고 있다. 비전(Radford et al., 2021; Zhai et al., 2021; Dehghani et al., 2023)이나 언어(Srivastava et al., 2023)와 같은 분야에서는 모델이 특정 임계 규모(critical scale)를 넘어설 때 비로소 새로운 능력이 발현되는 경우가 흔하다.
RL 분야에서도 유사한 잠재적 발현 현상(emergent phenomena)을 찾기 위한 연구가 활발히 진행되어 왔다(Srivastava et al., 2023). 그러나 기존 논문들은 대체로 매우 제한적인 성능 향상만 보고하며, 그것도 작은 모델이 어느 정도 성능을 내는 태스크에 국한되는 경우가 많다(Nauman et al., 2024b; Lee et al., 2024; Farebrother et al., 2024). 따라서 RL에서 제기되는 핵심 연구 질문은 다음과 같다. 과연 RL 모델의 네트워크 규모를 확장함으로써 다른 분야에서 관찰된 것처럼 성능이 도약하는 현상을 재현할 수 있는가?
언뜻 보기에는 매우 큰 RL 네트워크를 학습시키는 일이 어려운 것이 당연해 보인다. RL 문제는 관측 시퀀스가 길게 이어진 후에야 희소한 보상(sparse reward)과 같은 극히 제한된 피드백만 제공하므로, 파라미터 대비 피드백의 비율이 매우 낮기 때문이다. 이러한 관점은 기존의 통념(LeCun, 2016)과 여러 최신 모델들(Radford, 2018; Chen et al., 2020; Goyal et al., 2019)에서도 반영되어 있다. 즉, 대규모 AI 시스템은 주로 자기지도(self-supervised) 방식으로 학습되어야 하고, 강화학습은 이러한 모델을 미세조정(finetuning)하는 데만 사용해야 한다는 것이다.
실제로 최근 다른 분야에서 이루어진 주요 성과들은 대부분 자기지도 학습을 통해 달성되었다. 이는 컴퓨터 비전(Caron et al., 2021; Radford et al., 2021; Liu et al., 2024), 자연어 처리(NLP) 분야(Srivastava et al., 2023), 그리고 멀티모달 학습(Zong et al., 2024) 모두에서 동일하게 관찰된다. 따라서 강화학습 기법을 확장하려면 자기지도 학습 기제가 핵심 요소가 될 가능성이 높다.
본 논문에서는 강화학습을 확장하기 위한 구성 요소들을 체계적으로 탐구한다. 첫 번째 단계는 기존 통념을 다시 생각하는 것이다. 앞서 언급한 “강화학습”과 “자기지도 학습”은 서로 대립적인 학습 규칙이 아니라, 보상 함수나 시연(demonstrations)에 의존하지 않고도 탐색과 정책 학습을 수행할 수 있는 자기지도 강화학습(self-supervised RL) 시스템으로 결합될 수 있다(Eysenbach et al., 2021, 2022; Lee et al., 2022). 본 연구에서는 이러한 자기지도 RL 알고리즘 중 가장 단순한 형태 중 하나인 대비학습 기반 RL(contrastive RL, CRL)(Eysenbach et al., 2022)을 사용한다.
두 번째 단계는 이용 가능한 데이터의 양을 극적으로 확대하는 것이다. 이를 위해 최근 제안된 GPU 가속 기반 RL 프레임워크(Makoviychuk et al., 2021; Rutherford et al., 2023; Rudin et al., 2022; Bortkiewicz et al., 2024)를 기반으로 한다. 세 번째 단계는 네트워크 깊이를 크게 증가시키는 것으로, 기존 연구에서 일반적으로 사용되던 모델보다 최대 100배 더 깊은 네트워크를 활용한다. 이러한 깊은 네트워크를 안정적으로 학습시키기 위해서는 잔차 연결(residual connections)(He et al., 2015), 레이어 정규화(layer normalization)(Ba et al., 2016), Swish 활성화 함수(Ramachandran et al., 2018)와 같은 아키텍처 기법들을 적용해야 한다.
또한 본 연구의 실험에서는 배치 크기(batch size)와 네트워크 폭(network width)이 성능에 미치는 상대적 중요성 역시 분석한다.
본 연구의 주요 기여는 이러한 구성 요소들을 하나의 강화학습 기법으로 통합했을 때, 매우 강한 확장성이 실험적으로 드러난다는 점을 보이는 것이다.
• 경험적 확장성(Empirical Scalability): 전체 환경의 절반에서 성능이 20배 이상 향상되며, 기존의 표준 목표 조건(goal-conditioned) 기반 알고리즘들을 크게 능가한다. 이러한 성능 향상은 단순한 수치 증가가 아니라, 모델 규모가 커질 때 새롭게 등장하는 질적으로 구별되는 정책의 출현과 밀접하게 관련된다.
• 네트워크 깊이 확장(Scaling Depth in Network Architecture): 기존 RL 연구들은 주로 네트워크 폭(width)을 늘리는 데 집중했으며, 깊이(depth)를 확장했을 때는 성능 향상이 제한적이거나 오히려 성능이 저하되는 결과가 흔히 보고되었다(Lee et al., 2024; Nauman et al., 2024b). 반면 본 연구의 접근법은 네트워크 깊이 축(depth axis)에서의 확장을 실질적으로 가능하게 만들며, 단순히 폭을 확장할 때보다 더 큰 성능 향상을 이끌어낸다(섹션 4 참조).
• 경험적 분석(Empirical Analysis): 제안된 확장 접근 방식의 핵심 구성 요소들을 면밀히 분석하여, 어떤 요인들이 중요한 역할을 하는지 규명하고 새로운 통찰을 제공한다.
우리는 향후 연구가 본 연구의 기반 위에서 추가적인 구성 요소(building blocks)를 발굴하고 확장할 수 있을 것으로 기대한다.
2 관련 연구
자연어 처리(NLP)와 컴퓨터 비전(CV)은 최근 유사한 아키텍처(예: Transformer)와 공통 학습 패러다임(예: 자기지도 학습)을 채택하며 서로 수렴하고 있다. 이러한 결합된 흐름은 대규모 모델의 능력을 크게 확장시키는 데 핵심적 역할을 했다(Vaswani et al., 2017; Srivastava et al., 2023; Zhai et al., 2021; Dehghani et al., 2023; Wei et al., 2022). 반면, 강화학습(RL)에서 이와 유사한 수준의 발전을 이루는 일은 여전히 도전적이다.
여러 연구는 대규모 RL 모델의 확장을 어렵게 만드는 다양한 요인을 분석해 왔다. 여기에는 파라미터 활용 부족(parameter underutilization)(Obando-Ceron et al., 2024), 가소성과 용량 상실(plasticity and capacity loss)(Lyle et al., 2022, 2024), 데이터 희소성(data sparsity)(Andrychowicz et al., 2017; LeCun, 2016), 학습 불안정성(training instabilities)(Ota et al., 2021; Henderson et al., 2018; Van Hasselt et al., 2018; Nauman et al., 2024a) 등이 포함된다.
이러한 제약으로 인해 RL 모델 확장 관련 연구는 모방 학습(imitation learning)(Tuyls et al., 2024), 다중 에이전트 게임(multi-agent games)(Neumann and Gros, 2022), 언어 기반 RL(language-guided RL)(Driess et al., 2023; Ahn et al., 2022), 이산 행동 공간(discrete action spaces)(Obando-Ceron et al., 2024; Schwarzer et al., 2023) 등 특정 문제 영역에 제한되는 경우가 많다.
최근 연구들은 여러 유망한 방향을 제시하고 있다. 여기에는 새로운 아키텍처 패러다임(Obando-Ceron et al., 2024), 분산 학습(distributed training) 기법(Ota et al., 2021; Espeholt et al., 2018), 분포 기반 강화학습(distributional RL)(Kumar et al., 2023), 그리고 지식 증류(distillation)(Team et al., 2023) 등이 포함된다. 이러한 접근과 비교했을 때, 본 연구의 방법은 기존 자기지도 강화학습 알고리즘에 단순한 확장을 적용한 것이다.
이와 유사한 최신 연구로는 Lee et al. (2024)과 Nauman et al. (2024b)가 있으며, 이들은 잔차 연결(residual connections)을 적용해 더 넓은 네트워크(wider networks)의 학습을 용이하게 하고자 한다. 하지만 이들 연구는 네트워크 폭(width)에 주로 집중하고 있으며, 깊이를 늘렸을 때 얻을 수 있는 성능 향상은 제한적이라고 보고한다. 실제로 두 연구 모두 네 개의 MLP 레이어만 사용하는 얕은 아키텍처를 유지한다.
반면 본 연구에서는 네트워크 폭을 확장하면 성능이 향상된다는 점을 확인함과 동시에(섹션 4.4 참조), 깊이(depth) 방향으로의 확장 역시 가능하다는 점을 보여주며, 이는 폭만을 확장하는 것보다 더 강력한 성능 향상을 제공한다.
더 깊은 네트워크를 학습하려는 시도로는 Farebrother et al. (2024)의 연구가 대표적이다. 이들은 TD 목표(TD objective)를 이산화(discretization)하여 범주형 교차 엔트로피(categorical cross-entropy) 손실로 변환함으로써, 가치 기반 RL(value-based RL)을 분류 문제로 재정의하였다. 이러한 접근은 분류 기반 접근법이 회귀 기반 방식보다 더 견고하고 안정적이며, 따라서 확장성 측면에서도 우수할 가능성이 있다는 가설에 기반한다(Torgo and Gama, 1996; Farebrother et al., 2024).
본 연구에서 사용하는 CRL(Contrastive RL) 알고리즘 역시 실질적으로 교차 엔트로피 기반 손실을 사용한다(Eysenbach et al., 2022). 구체적으로, CRL의 InfoNCE 목적 함수는 교차 엔트로피 손실의 일반화 형태이며, 현재 상태와 행동이 목표 상태로 이어지는 동일한 궤적(trajectory)에 속하는지 여부를 분류(classification)하는 방식으로 RL 문제를 해결한다.
이런 관점에서 본 연구는 NLP 분야에서 교차 엔트로피 기반 분류가 대규모 모델 확장의 핵심 역할을 했던 것처럼, RL에서도 분류 기반 접근법이 중요한 구성 요소가 될 수 있음을 시사하는 두 번째 실증적 근거를 제공한다.
3 사전 지식(Preliminaries)
본 섹션에서는 목표 조건(goal-conditioned) 강화학습과 대비학습 기반 강화학습(contrastive RL)에 사용되는 기호와 정의를 소개한다. 본 연구의 초점은 온라인 강화학습(online RL)에 있으며, 여기서는 리플레이 버퍼(replay buffer)가 최신 궤적(trajectory)을 저장하고, 크리틱(critic)은 자기지도(self-supervised) 방식으로 학습된다.
목표 조건(goal-conditioned) 강화학습
목표 조건 MDP는
ℳ_g = (𝒮, 𝒜, p₀, p, p_g, r_g, γ)
와 같은 튜플로 정의된다. 여기서 에이전트는 임의의 목표에 도달하기 위해 환경과 상호작용한다(Kaelbling, 1993; Andrychowicz et al., 2017; Blier et al., 2021).
각 시간 단계 t에서 에이전트는 상태
sₜ ∈ 𝒮
를 관측하고, 그에 대응하는 행동
aₜ ∈ 𝒜
를 수행한다. 초기 상태는
p₀(s₀)
에서 샘플링되며, 상호작용의 동역학은 전이 확률
p(sₜ₊₁ ∣ sₜ, aₜ)
로 정의된다.
목표 g ∈ 𝒢 는 목표 공간 𝒢 에 속하며, 상태 공간 𝒮 와는 사상
f: 𝒮 → 𝒢
을 통해 연관된다. 예를 들어, 𝒢 는 상태 벡터의 일부 차원을 나타낼 수도 있다. 목표에 대한 사전분포(prior)는
p_g(g)
로 정의된다.
보상 함수는 다음 단계에서 목표에 도달할 확률 밀도로 정의된다.
r_g(sₜ, aₜ) ≜ (1 − γ) p(sₜ₊₁ = g ∣ sₜ, aₜ),
여기서 γ는 할인 계수(discount factor)이다.
이 설정에서 목표 조건 정책
π(a ∣ s, g)
은 환경의 현재 관찰 s와 목표 g를 모두 입력으로 받는다.
할인된 상태 방문 분포(discounted state visitation distribution)는 다음과 같이 정의된다.
p^π_γ(⋅ ∣ ⋅, g)(s) ≜ (1 − γ) ∑_{t=0}^{∞} γᵗ p^π_t(⋅ ∣ ⋅, g)(s),
여기서 p^π_t(s)는 정책 π가 목표 g 조건 하에서 정확히 t스텝 후 상태 s를 방문할 확률이다.
이 표현은 정책 π(⋅ ∣ ⋅, g)의 Q-함수와 정확히 동일하며, 목표 보상 r_g에 대해 다음과 같이 쓸 수 있다.
Q^π_g(s, a) ≜ p^π_γ(⋅ ∣ ⋅, g)(g ∣ s, a).
목표는 기대 보상을 최대화하는 것이다.
max_π 𝔼_{p₀(s₀), p_g(g), π(⋅ ∣ ⋅, g)} [ ∑_{t=0}^{∞} γᵗ r_g(sₜ, aₜ) ]
(1)
대비학습 기반 강화학습(Contrastive Reinforcement Learning)
본 연구의 실험에서는 대비학습 기반 강화학습(contrastive RL) 알고리즘(Eysenbach et al., 2022)을 사용해 목표 조건 강화학습 문제를 해결한다. Contrastive RL은 액터 크리틱(actor-critic) 방식으로 구성되며,
f_{ϕ,ψ}(s, a, g)를 크리틱(critic),
π_θ(a ∣ s, g)를 정책(policy)으로 정의한다.
크리틱은 두 개의 신경망으로 구성되며, 하나는 상태-행동 쌍 임베딩 ϕ(s, a), 다른 하나는 목표 임베딩 ψ(g)를 출력하도록 한다. 크리틱의 출력은 두 임베딩 간의 L2 거리로 정의된다.
f_{ϕ,ψ}(s, a, g) = ‖ϕ(s, a) − ψ(g)‖₂.
크리틱은 InfoNCE 목적 함수(Sohn, 2016)를 사용해 학습되며, 이는 이전 연구(Eysenbach et al., 2021, 2022; Zheng et al., 2023, 2024; Myers et al., 2024; Bortkiewicz et al., 2024)와 동일하다.
학습은 배치 ℬ에서 이루어지며, 여기서
sᵢ, aᵢ, gᵢ는 동일한 궤적 내에서 샘플된 상태, 행동, 목표(미래 상태)를 의미한다.
반면 gⱼ는 서로 다른 무작위 궤적으로부터 샘플된 목표이다.
목적 함수는 다음과 같이 정의된다.
min_{ϕ,ψ} 𝔼_ℬ [
− ∑{i=1}^{|ℬ|} log (
e^{f{ϕ,ψ}(sᵢ, aᵢ, gᵢ)}
/ ∑{j=1}^{K} e^{f{ϕ,ψ}(sᵢ, aᵢ, gⱼ)}
)
].
정책 π_θ(a ∣ s, g)는 크리틱 출력을 최대화하도록 학습된다.
max_{π_θ} 𝔼_{p₀(s₀), p(s_{t+1} ∣ s_t, a_t), p_g(g), π_θ(a ∣ s, g)}
[ f_{ϕ,ψ}(s, a, g) ].
Contrastive RL(CRL)의 핵심 차이점은 ‘학습 신호의 형태(보상)’와 ‘Q 함수의 역할(거리 기반 목적)’이 달라졌다는 것이지만, 근본적인 강화학습 프레임워크 자체는 변화가 거의 없다.
즉, 이론적 구조는 RL 그대로인데, 신호를 만드는 방식과 해석이 바뀐 것이다.
아래에서 너가 궁금해하는 두 가지 차이가 기존 RL 이론과 정확히 어떻게 다른지 구조적으로 설명해줄게.
2) 보상 처리 방식이 다르다
기존 RL에서는
- 보상 r(s, a, s')는 환경이 직접 제공하며,
- 에이전트는 그 보상을 누적해서 expected return을 최대화한다.
Contrastive RL에서는
환경 보상이 존재하지 않기 때문에 보상 자체를 재정의한다.
즉, CRL의 보상은
- 같은 trajectory의 미래 상태 gᵢ → positive
- 다른 trajectory의 목표 gⱼ → negative
- 이 둘을 구분하는 분류(classification) 문제로 변환
수식적으로 보상을 직접 쓰지 않고, InfoNCE loss가 사실상의 보상 역할을 대체한다.
이게 기존 RL 이론에서 가장 다른 부분이다.
하지만 “보상으로부터 정책을 최적화한다”라는 RL의 틀은 그대로 유지된다.
즉:
전통적 RL:
maximize E[∑ γᵗ r(sₜ, aₜ)]
Contrastive RL:
maximize f(s, a, g) = − InfoNCE(s,a,g)
둘 다 “어떤 신호를 최대화”하려는 동일한 목적 구조지만,
그 신호가 어디에서 오는지가 완전히 다르다.
3) Q 함수가 InfoNCE 기반 거리로 대체된 것뿐
기존 RL의 Q(s,a)
Q(s,a) = 기대 보상(return)
정책은 Q를 최대화한다.
CRL의 f(s,a,g)
f(s,a,g) = ‖ϕ(s,a) − ψ(g)‖₂
(가까울수록 좋은 행동이라고 간주)
이 f(s,a,g)가 사실상 Q(s,a,g)를 대체한 것이다.
하지만
“정책이 어떤 스칼라 값을 최대화한다”
라는 구조는 RL과 동일하다.
즉:
- 기존 Q는 “얼마나 많은 보상을 받을 것인가”
- CRL Q는 “목표에 도달할 trajectory에 포함될 가능성이 높은가”
이 두 개는 해석만 다르고 역할은 같다.
핵심적인 차이를 다시 정리하면
기존 RL
- 보상 r(s,a,s')는 외부에서 주어짐
- Q(s,a)는 “기대 보상”
- TD-learning으로 Q를 학습
- 정책은 Q를 최대화
Contrastive RL
- 외부 보상이 없음
- InfoNCE가 보상 역할을 수행
- Q 대신 f(s,a,g)=distance 기반 scoring
- 정책은 f를 최대화
즉, Q 함수의 정의가 달라졌지만 하는 일은 똑같다.
그럼 “새로운 이론인가?”
아니야. 완전히 새로운 이론은 아니다.
CRL은 본질적으로
“보상이 없는 환경에서 스스로 보상을 정의하여 RL을 수행하는 기법”
이고,
학습 구조는 기존 RL 프레임워크 그대로다.
새로운 점은 오히려 다음에 있다:
- 보상 = 대조학습(contrastive learning)
- Q = 거리 기반 score
- 목적함수 = InfoNCE
- 구체적 수식은 representation learning에서 가져온 것
즉,
기존 RL + 대조학습(InfoNCE) = Contrastive RL
이라는 조합이다.
결론
- 보상 처리 방식 변경
- Q 정의의 변경
이 두 가지가 주요 차이점이지만,
강화학습의 이론적 구조 자체는 거의 달라지지 않았다.
새로운 “철학”보다는
“보상을 스스로 만드는 self-supervised RL”이라는 확장에 가깝다.
잔차 연결(Residual Connections)
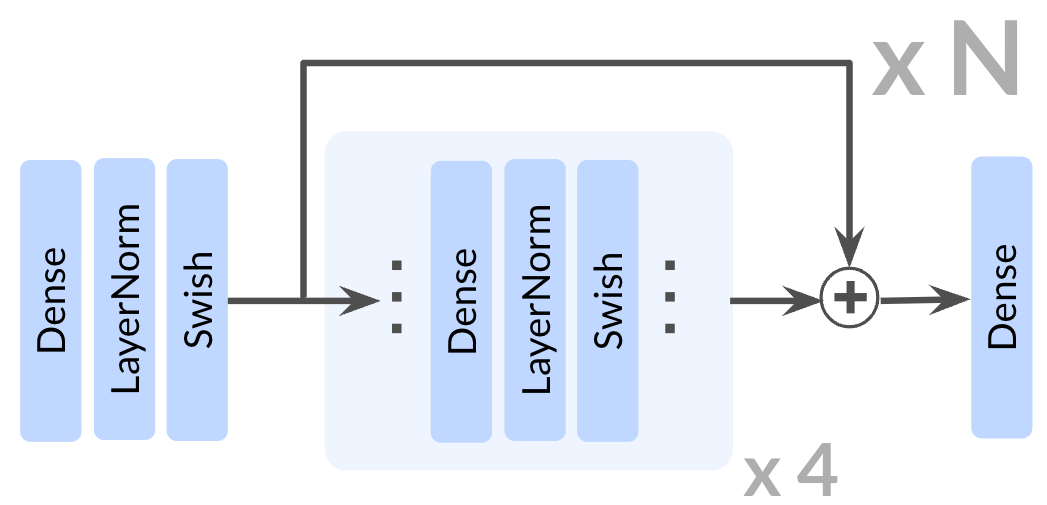
그림 2: 아키텍처. 본 연구의 접근법은 Contrastive RL 알고리즘의 액터와 크리틱 네트워크 모두에 잔차 연결(residual connections)을 통합한다. 잔차 아키텍처의 깊이는 잔차 블록 전체에 포함된 Dense 레이어 수로 정의되며, 하나의 잔차 블록이 4개의 레이어로 구성되므로 전체 깊이는 4N이 된다.
우리는 기존 연구에서 RL에 성공적으로 적용된 잔차 연결(He et al., 2015)(Farebrother et al., 2024; Lee et al., 2024; Nauman et al., 2024b)을 본 모델 아키텍처에 도입한다. 잔차 블록은 주어진 표현 𝐡ᵢ에 대해 학습된 잔차 함수 Fᵢ(𝐡ᵢ)를 더함으로써 변환을 수행한다. 수식적으로는 다음과 같다.
𝐡ᵢ₊₁ = 𝐡ᵢ + Fᵢ(𝐡ᵢ)
여기서
• 𝐡ᵢ₊₁는 출력 표현,
• 𝐡ᵢ는 입력 표현,
• Fᵢ(𝐡ᵢ)는 신경망(예: 다중 레이어)을 통해 학습된 변환을 의미한다.
이 덧셈 구조는 네트워크가 입력 전체를 새롭게 변환하는 것이 아니라, 입력에 대한 수정(modification) 을 학습하도록 유도하여 이전 레이어에서 얻은 유용한 특징을 유지하는 데 도움을 준다.
잔차 연결은 shortcut 경로를 도입함으로써 기울기 전파를 개선하며(He et al., 2016; Veit et al., 2016), 이를 통해 매우 깊은 모델을 더 효과적으로 학습할 수 있게 한다.
4 실험
4.1 실험 설정
환경(Environments).
모든 강화학습 실험은 JaxGCRL 코드베이스(Bortkiewicz et al., 2024)를 사용하여 수행되며, 이는 Brax(Freeman et al., 2021) 및 MJX(Todorov et al., 2012) 환경을 기반으로 한 빠른 온라인 GCRL 실험을 가능하게 한다. 사용된 환경들은 보행(locomotion), 내비게이션(navigation), 로봇 조작(manipulation) 등 다양한 종류이며, 구체적 설명은 부록 B에 제공한다.
보상은 희소 보상(sparse reward) 설정을 사용하며, 에이전트가 목표 근처에 있을 때만
r = 1
을 부여한다. 평가 시에는 1000 스텝 중 에이전트가 목표 근처에 있었던 스텝 수를 측정한다. 알고리즘의 단일 성능 지표를 보고할 때는 학습 마지막 5 에폭의 평균 점수를 사용한다.
아키텍처 구성 요소(Architectural Components)
본 연구에서는 ResNet 아키텍처(He et al., 2015)의 잔차 연결(residual connections)을 적용하며, 각 잔차 블록은 다음 세 구성 요소를 4회 반복하여 구성된다.
- Dense layer
- Layer Normalization(Ba et al., 2016)
- Swish activation(Ramachandran et al., 2018)
잔차 연결은 그림 2에서 보듯이 잔차 블록의 마지막 활성화 함수 바로 뒤에 적용된다.
본 논문에서 네트워크 깊이는 아키텍처 전체에서 잔차 블록 안에 포함된 Dense layer의 총 개수로 정의한다.
모든 실험에서 깊이(depth)는 다음 세 네트워크를 공동으로 확장(scale jointly)하는 구성 값을 의미한다.
- actor network
- critic state-action encoder
- critic goal encoder
단, 섹션 4.4의 ablation 실험은 예외다.
4.2 Contrastive RL에서의 깊이 확장(Scaling Depth)
먼저 네트워크 깊이를 증가시키는 것이 성능 향상에 어떤 영향을 미치는지 분석한다. JaxGCRL 벤치마크와 관련 선행 연구(Lee et al., 2024; Nauman et al., 2024b; Zheng et al., 2024)에서는 모두 깊이 4의 MLP를 사용하고 있으며, 이에 따라 이를 본 연구의 기준선(baseline)으로 채택한다. 반면, 본 연구에서는 깊이 8, 16, 32, 64의 네트워크를 체계적으로 비교 분석한다.
그림 1의 결과는 네트워크 깊이가 증가할수록 보행(locomotion), 내비게이션(navigation), 로봇 조작(manipulation) 등 다양한 태스크 전반에서 성능이 크게 향상됨을 보여준다. 기존 연구에서 일반적으로 사용되던 4-레이어 모델과 비교했을 때, 더 깊은 네트워크는 로봇 조작 태스크에서 2~5배의 성능 향상을 달성했으며, Ant U4-Maze 및 Ant U5-Maze와 같은 장기 시계열(long-horizon) 미로 태스크에서는 20배 이상의 성능 향상을 보였다. 특히 휴머노이드(humanoid) 기반 태스크에서는 50배를 초과하는 성능 향상이 관찰되었다. 깊이 64까지의 전체 성능 비교 결과는 표 1에 제시되어 있다.
그림 12에서는 동일한 10개 환경에 대해 SAC, SAC+HER, TD3+HER, GCBC, GCSL과 비교한 결과를 제시한다. CRL을 확장(scale)하면 성능이 크게 향상되며, 10개 태스크 중 8개에서 모든 다른 기준선 알고리즘을 능가한다. 유일한 예외는 휴머노이드 미로 환경에서의 SAC로, 초기 학습 단계에서는 더 높은 샘플 효율성을 보이지만, 충분히 학습이 진행되면 확장된 CRL 역시 이에 준하는 성능에 도달한다.
이러한 결과는 Contrastive RL 알고리즘의 네트워크 깊이를 확장하는 것만으로도 목표 조건 강화학습에서 최신 수준(state-of-the-art)의 성능을 달성할 수 있음을 보여준다.
4.3 깊이에 따른 정책의 발현(Emergent Policies Through Depth)

그림 3: 네트워크 깊이를 증가시키면 새로운 능력이 발현된다.
행 1: 깊이 4의 에이전트는 쓰러지거나 몸을 던져 목표를 향한다.
행 2: 깊이 16의 에이전트는 직립 보행으로 이동한다.
행 3: 깊이 64의 에이전트는 버둥거리다 넘어지며 실패한다.
행 4: 깊이 256의 에이전트는 곡예에 가까운 동작으로 벽을 넘는다.
그림 1의 성능 곡선을 자세히 살펴보면 흥미로운 패턴이 드러난다. 네트워크 깊이가 증가함에 따라 성능이 점진적으로 향상되는 것이 아니라, 특정 임계 깊이(critical depth)에 도달했을 때 성능이 급격히 도약하는 현상이 관찰된다(그림 6에서도 확인 가능). 이러한 임계 깊이는 환경에 따라 다르며, Ant Big Maze에서는 8층, Humanoid U-Maze 태스크에서는 64층 수준에서 나타난다. 또한, 1024층과 같은 훨씬 더 깊은 설정에서도 추가적인 성능 도약이 발생함을 확인했다(섹션 4.4, Testing Limits 참조).
이러한 관찰을 바탕으로, 우리는 서로 다른 깊이에서 학습된 정책을 시각화하였고, 그 결과 질적으로 완전히 다른 기술과 행동이 깊이에 따라 발현됨을 확인했다. 이러한 현상은 특히 휴머노이드 기반 태스크에서 두드러지며, 그림 3에 그 예시를 제시한다.
깊이 4의 네트워크는 에이전트가 넘어지거나 몸을 던져 목표에 접근하는 수준의 매우 원시적인 정책만을 학습한다. 깊이가 16에 도달해야 비로소 에이전트는 직립 보행으로 목표를 향해 이동하는 능력을 획득한다. Humanoid U-Maze 환경에서는 깊이 64의 네트워크가 중간에 위치한 벽을 우회하지 못하고 바닥에 쓰러지는 모습을 보인다. 놀랍게도 깊이 256에 이르면, 에이전트는 Humanoid U-Maze에서 이전과는 전혀 다른 독창적인 행동을 학습한다. 여기에는 몸을 앞으로 접어 지렛대처럼 사용해 벽을 넘는 동작이나, 중간 장애물 위에서 앉은 자세로 이동하며 목표를 향해 기어가는 행동이 포함된다(이 중 하나의 정책이 그림 3의 네 번째 행에 제시되어 있다).
저자들이 아는 한, 이는 휴머노이드 환경에서 이러한 행동을 보고한 최초의 목표 조건 강화학습 접근법이다.
4.4 CRL 확장에서 중요한 요소는 무엇인가
폭(Width) vs. 깊이(Depth)
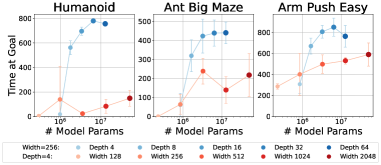
그림 4: 네트워크 폭과 깊이 확장의 비교. 기존 연구(Lee et al., 2024; Nauman et al., 2024b)에서는 네트워크 폭을 늘리는 것이 성능 향상에 도움이 된다고 보고하였다. 본 연구에서도 폭 확장이 효과적임을 확인하지만, 기존 연구와 달리 깊이 확장 역시 가능하며, 그 효과는 폭 확장보다 더 크다는 점을 보여준다. 예를 들어 Humanoid 환경에서는 폭을 2048까지 늘린 경우(깊이=4)가, 깊이를 8로 단순히 두 배 늘린 경우(폭=256)보다 성능이 낮다. 이러한 깊이 확장의 상대적 이점은 관측 차원(observation dimensionality)이 커질수록 더욱 두드러진다.
기존 문헌에서는 네트워크 폭 확장이 효과적일 수 있음이 이미 보고된 바 있다(Lee et al., 2024; Nauman et al., 2024b). 그림 4에서도 폭을 확장하면 성능이 향상되는 경향을 확인할 수 있으며, 깊이를 4로 고정했을 때 넓은 네트워크가 일관되게 더 나은 성능을 보인다. 그러나 깊이는 폭보다 더 강력한 확장 축으로 작용한다. 폭을 256으로 고정한 상태에서 깊이를 8로 단순히 두 배 늘리는 것만으로도, 세 가지 모든 환경에서 가장 넓은 네트워크를 능가하는 성능을 달성한다.
깊이 확장의 이점은 Humanoid 환경(관측 차원 268)에서 가장 크게 나타나며, 그 다음으로 Ant Big Maze(차원 29), Arm Push Easy(차원 17) 순으로 나타난다. 이는 관측 차원이 커질수록 깊이 확장의 상대적 이득이 증가할 가능성을 시사한다.
추가로 주목할 점은 파라미터 수의 스케일링 특성이다. 파라미터 수는 폭에 대해서는 선형적으로 증가하지만, 깊이에 대해서는 이차적으로 증가한다. 예를 들어, 4개의 MLP 레이어와 2048개의 히든 유닛을 가진 네트워크는 약 3,500만 개의 파라미터를 가지는 반면, 깊이 32에 히든 유닛 256을 가진 네트워크는 약 200만 개의 파라미터만을 필요로 한다. 따라서 고정된 FLOP 계산 예산이나 특정 메모리 제약 조건 하에서는, 깊이 확장이 네트워크 성능을 향상시키는 데 있어 계산 효율 측면에서 더 유리한 접근법이 될 수 있다.
액터 네트워크와 크리틱 네트워크 확장(Scaling the Actor vs. Critic Networks)

그림 5: 임계 깊이와 잔차 연결. 네트워크 깊이를 점진적으로 증가시키면 성능은 소폭만 향상된다(왼쪽). 그러나 잔차 연결이 적용된 네트워크에서 특정 임계 깊이에 도달하면 성능이 급격히 향상된다(오른쪽).

그림 6: 액터 vs. 크리틱. Arm Push Easy 환경에서는 크리틱 확장이 더 효과적이며, Ant Big Maze에서는 액터 확장이 더 중요하다. Humanoid 환경에서는 액터와 크리틱 모두를 확장해야 한다. 이러한 결과는 CRL에서 액터와 크리틱 확장이 서로 보완적으로 작용할 수 있음을 시사한다.
액터 및 크리틱 네트워크의 확장이 성능에 미치는 영향을 분석하기 위해, 그림 6에서는 세 가지 환경에 대해 액터와 크리틱 깊이의 다양한 조합에서의 최종 성능을 제시한다. 기존 연구(Nauman et al., 2024b; Lee et al., 2024)는 주로 크리틱 네트워크 확장에 집중했으며, 액터를 확장하면 오히려 성능이 저하된다고 보고하였다.
반면 본 연구에서는 세 환경 중 두 곳(Humanoid, Arm Push Easy)에서는 크리틱 확장이 더 큰 영향을 미치지만, 액터 네트워크를 함께 확장할 경우 추가적인 성능 향상이 발생함을 확인했다. 특히 Ant Big Maze 환경에서는 액터 확장이 더 중요한 요소로 작용했다. 이러한 결과는 액터와 크리틱 네트워크를 모두 확장하는 것이 성능 향상에 있어 상호 보완적인 역할을 할 수 있음을 시사한다.
깊은 네트워크가 배치 크기 확장을 가능하게 함
(Deep Networks Unlock Batch Size Scaling)
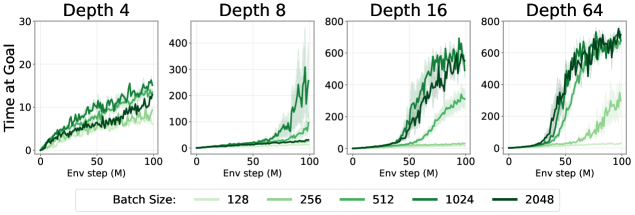
그림 7: 더 깊은 네트워크는 배치 크기 확장을 가능하게 한다. Humanoid 환경에서 네트워크 깊이가 4에서 64로 증가함에 따라, 더 큰 네트워크가 배치 크기 확장을 효과적으로 활용하여 추가적인 성능 향상을 달성할 수 있음을 확인했다.
배치 크기(batch size) 확장은 다른 기계학습 분야에서는 이미 잘 확립된 기법이다(Chen et al., 2022; Zhang et al., 2024). 그러나 이러한 접근은 강화학습(RL)에서는 그 효과가 제한적이었으며, 일부 선행 연구에서는 가치 기반 RL에서 오히려 부정적인 영향을 보고하기도 했다(Obando-Ceron et al., 2023). 실제로 본 연구의 실험에서도, 기존 CRL 네트워크에서 배치 크기만 단순히 증가시킬 경우 성능 차이는 매우 제한적임을 확인했다(그림 7, 좌측 상단).
겉보기에는 이는 직관에 반하는 결과처럼 보일 수 있다. 강화학습은 일반적으로 학습 데이터 한 샘플당 포함된 정보량이 적기 때문에(LeCun, 2016), 배치 손실이나 기울기의 분산이 클 가능성이 높고, 이를 보완하기 위해 더 큰 배치 크기가 필요할 것처럼 보이기 때문이다. 그러나 이러한 가정은 해당 모델이 실제로 더 큰 배치 크기를 활용할 수 있는 충분한 표현력을 갖추고 있는지에 달려 있다. 대규모 확장이 성공적으로 이루어진 다른 머신러닝 분야에서는, 충분히 큰 모델과 결합될 때 배치 크기 확장이 가장 큰 이점을 제공하는 것이 일반적이다(Chen et al., 2022; Zhang et al., 2024). 즉, RL에서 전통적으로 사용되어 온 작은 모델들이 배치 크기 확장의 잠재적 이점을 가리고 있었을 가능성이 있다.
이 가설을 검증하기 위해, 우리는 서로 다른 깊이를 가진 네트워크에 대해 배치 크기 증가 효과를 분석했다. 그림 7에서 보듯이, 네트워크 깊이가 커질수록 배치 크기 확장이 실질적인 성능 향상으로 이어진다. 이러한 결과는 네트워크 용량을 확장함으로써, 동시에 더 큰 배치 크기의 이점을 활용할 수 있음을 시사하며, 이는 자기지도 강화학습 확장을 위한 중요한 구성 요소가 될 수 있음을 보여준다.
1000층 이상의 네트워크로 Contrastive RL 학습하기
다음으로, 네트워크 깊이를 64층을 넘어 더 증가시켰을 때 성능이 추가로 향상되는지 분석한다. 이를 위해 벤치마크 환경 중 가장 난이도가 높고, 깊이 확장의 효과가 가장 크게 나타나는 Humanoid 미로 태스크를 사용한다. 그림 12에 제시된 결과에 따르면, Humanoid U-Maze 환경에서 네트워크 깊이가 256층과 1024층에 도달할 때까지 성능이 지속적으로 크게 향상된다. 계산 자원의 제약으로 인해 1024층을 초과하는 실험은 수행하지 못했지만, 특히 가장 어려운 태스크에서는 더 큰 깊이를 사용할 경우 추가적인 성능 향상이 이어질 것으로 기대된다.
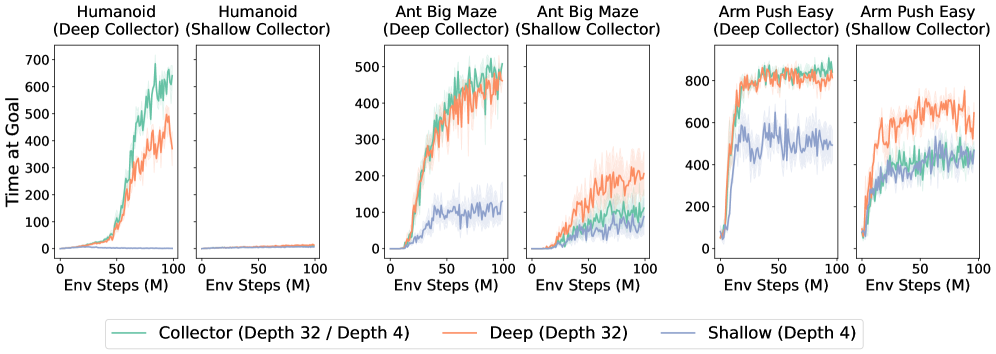
그림 8: 깊이 확장에서 탐색(exploration) 과 표현력(expressivity) 이 각각 어떤 역할을 하는지 분리해 분석하기 위해, 세 개의 네트워크를 병렬로 학습한다. 하나는 데이터를 수집하는 “collector”이고, 나머지 두 개는 collector가 공유하는 리플레이 버퍼만을 사용해 학습하는 하나의 깊은 learner와 하나의 얕은 learner이다. 세 환경 모두에서, 깊은 collector를 사용해 충분한 데이터 커버리지를 확보한 경우, 깊은 learner가 얕은 learner보다 더 우수한 성능을 보였으며, 이는 탐색 조건이 동일할 때 표현력이 핵심적인 요소임을 의미한다. 반대로 얕은 collector를 사용해 탐색이 충분하지 않은 경우에는, 깊은 learner조차도 제한적인 데이터 커버리지의 한계를 극복하지 못했다. 이러한 결과는 깊이 확장의 이점이 개선된 탐색과 증가된 표현력이 함께 작용할 때 나타난다는 점을 시사한다.
4.5 왜 스케일링이 발생하는가
깊이는 대비 표현(Contrastive Representations)을 강화한다

그림 9: 더 깊은 Q-함수는 질적으로 다른 특성을 보인다. U4-Maze 환경에서 시작 위치와 목표 위치는 각각 ⊚∙와 G 기호로 표시되어 있으며, 시각화된 Q 값은 학습된 표현 공간에서의 L2 거리로 계산된다. 즉,
Q(s, a, g) = ‖ϕ(s, a) − ψ(g)‖₂ 이다.
얕은 깊이 4 네트워크(왼쪽)는 미로 벽이 존재함에도 불구하고 유클리드 거리 기반 근접성에 단순히 의존하여, 시작 지점 근처에서도 높은 Q 값을 보인다. 반면 깊이 64 네트워크(오른쪽)는 목표 지점 주변에 높은 Q 값을 집중시키고, 미로 내부를 따라 점진적으로 감소하는 분포를 형성한다.
장기 시계열(long-horizon) 설정은 강화학습에서 오랫동안 해결이 어려운 문제로 남아 있었으며, 특히 보조 보상(auxiliary reward)이 전혀 제공되지 않는 비지도 목표 조건 강화학습 환경에서는 그 어려움이 더욱 크다(Gupta et al., 2019). U-Maze 계열 환경은 효과적인 탐색을 위해 미로의 전체 구조에 대한 전역적 이해를 요구한다.
본 연구에서는 Ant U-Maze 환경의 변형인 U4-Maze를 고려하는데, 이 환경에서는 에이전트가 목표에 도달하기 위해 처음에는 목표와 반대 방향으로 이동한 뒤, 우회 경로를 따라 돌아가야 한다. 그림 9에서 보듯이, 얕은 네트워크(깊이 4)와 깊은 네트워크(깊이 64)는 질적으로 뚜렷이 다른 행동을 보인다. 크리틱 인코더의 표현으로부터 계산된 Q 값 시각화를 살펴보면, 깊이 4 네트워크는 벽이 직접 경로를 차단하고 있음에도 불구하고 목표까지의 유클리드 거리를 Q 값의 대리 지표로 사용하는 경향을 보인다. 반면 깊이 64의 크리틱 네트워크는 훨씬 풍부한 표현을 학습하여, 미로의 위상(topology)을 효과적으로 포착하며, 이는 미로 내부 경계를 따라 형성된 높은 Q 값의 궤적으로 확인할 수 있다.
이러한 결과는 네트워크 깊이를 증가시킬수록 학습되는 표현이 더욱 풍부해지며, 그 결과 깊은 네트워크가 환경의 구조적 특성을 더 잘 이해하고, 자기지도 방식으로 상태 공간 전반을 보다 포괄적으로 커버할 수 있음을 시사한다.
깊이는 탐색과 표현력을 상호 보완적으로 강화한다
(Depth Enhances Exploration and Expressivity in a Synergized Way)
앞선 결과들은 더 깊은 네트워크가 상태–행동 공간을 더 폭넓게 커버함을 시사했다. 스케일링이 왜 효과적인지 이해하기 위해, 우리는 성능 향상이 단순히 더 나은 데이터 덕분인지, 아니면 다른 요인들과 결합되어 나타나는지 여부를 분석하고자 했다. 이를 위해 그림 8과 같은 실험을 설계하였다. 이 실험에서는 세 개의 네트워크를 병렬로 학습한다. 하나는 환경과 직접 상호작용하며 모든 경험을 공유 리플레이 버퍼에 저장하는 “collector” 네트워크이고, 나머지 두 개는 각각 깊은 learner와 얕은 learner이다. 중요한 점은 이 두 learner가 스스로 데이터를 수집하지 않고, 오직 collector가 생성한 리플레이 버퍼의 데이터만으로 학습한다는 것이다.
이 설계는 데이터 분포를 동일하게 유지한 채 모델의 용량만을 변화시키므로, 깊은 learner와 얕은 learner 사이의 성능 차이는 탐색(exploration)이 아니라 표현력(expressivity)의 차이에서 비롯된 것임을 보장한다. collector가 깊은 네트워크(예: 깊이 32)인 경우, 세 가지 모든 환경에서 깊은 learner가 얕은 learner를 크게 능가하는 성능을 보였으며, 이는 깊은 네트워크의 표현력이 핵심적임을 의미한다. 반대로 얕은 collector(예: 깊이 4)를 사용한 경우에는 탐색이 충분히 이루어지지 않아 리플레이 버퍼가 낮은 커버리지의 경험으로 채워지며, 이 상황에서는 깊은 learner와 얕은 learner 모두 성능이 저조하고 큰 차이를 보이지 않는다. 이는 깊은 네트워크의 추가적인 용량만으로는 불충분한 데이터 커버리지의 한계를 극복할 수 없음을 시사한다.
결과적으로, 깊이 확장은 탐색과 표현력을 상호 보완적으로 강화한다. 더 강한 학습 용량은 더 광범위한 탐색을 유도하고, 충분한 데이터 커버리지는 강력한 학습 용량의 잠재력을 온전히 발휘하는 데 필수적이다. 이 두 요소가 함께 작용할 때 성능 향상이 달성된다.
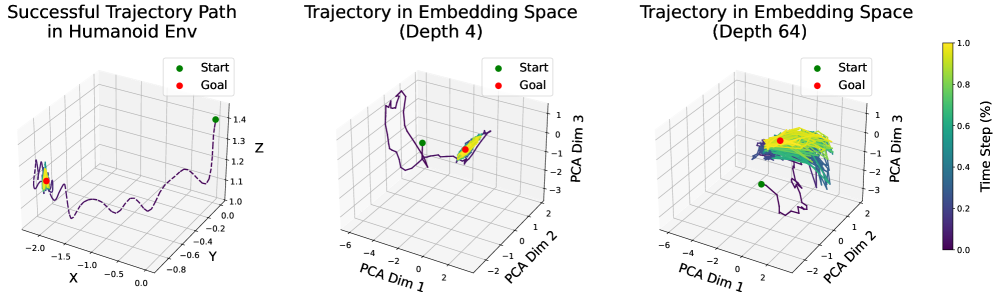
그림 10: Humanoid 태스크에서 성공적인 궤적을 따라, 얕은 네트워크(깊이 4)와 깊은 네트워크(깊이 64)의 상태–행동 임베딩을 시각화한다. 목표 근처에서 깊은 네트워크의 임베딩은 곡면을 따라 넓게 확장되는 반면, 얕은 네트워크의 임베딩은 좁은 군집을 형성한다. 이는 깊은 네트워크가 상태 공간 중 더 자주 방문되고 태스크 성공에 중요한 영역에 더 많은 표현 용량을 할당하고 있을 가능성을 시사한다.
깊은 네트워크는 목표 근처 상태에 더 큰 표현 용량을 할당하는 법을 학습한다
그림 10에서는 Humanoid 환경에서 성공적인 하나의 궤적을 선택하여, 그 궤적을 따라 상태–행동 인코더의 임베딩을 얕은 네트워크와 깊은 네트워크 각각에 대해 시각화한다. 얕은 네트워크(깊이 4)는 목표 근처의 상태들을 매우 조밀하게 하나의 군집으로 묶는 경향이 있는 반면, 깊은 네트워크는 훨씬 더 넓게 퍼진(spread out) 표현을 생성한다.
이러한 차이는 중요한 의미를 갖는다. 자기지도 학습 환경에서는, 무작위 상태들과 구분되어야 할 중요한 상태, 특히 미래 상태나 목표와 직접적으로 관련된 상태들이 표현 공간에서 명확히 분리되기를 원한다. 다시 말해, 이러한 핵심 영역에 더 많은 표현 용량을 할당하는 것이 바람직하다.
이 결과는 깊은 네트워크가 다운스트림 태스크 수행에 가장 중요한 상태 영역에 대해 표현 용량을 보다 효과적으로 배분하는 법을 학습할 수 있음을 시사한다.
더 깊은 네트워크는 부분 경험 결합(Partial Experience Stitching)을 가능하게 한다
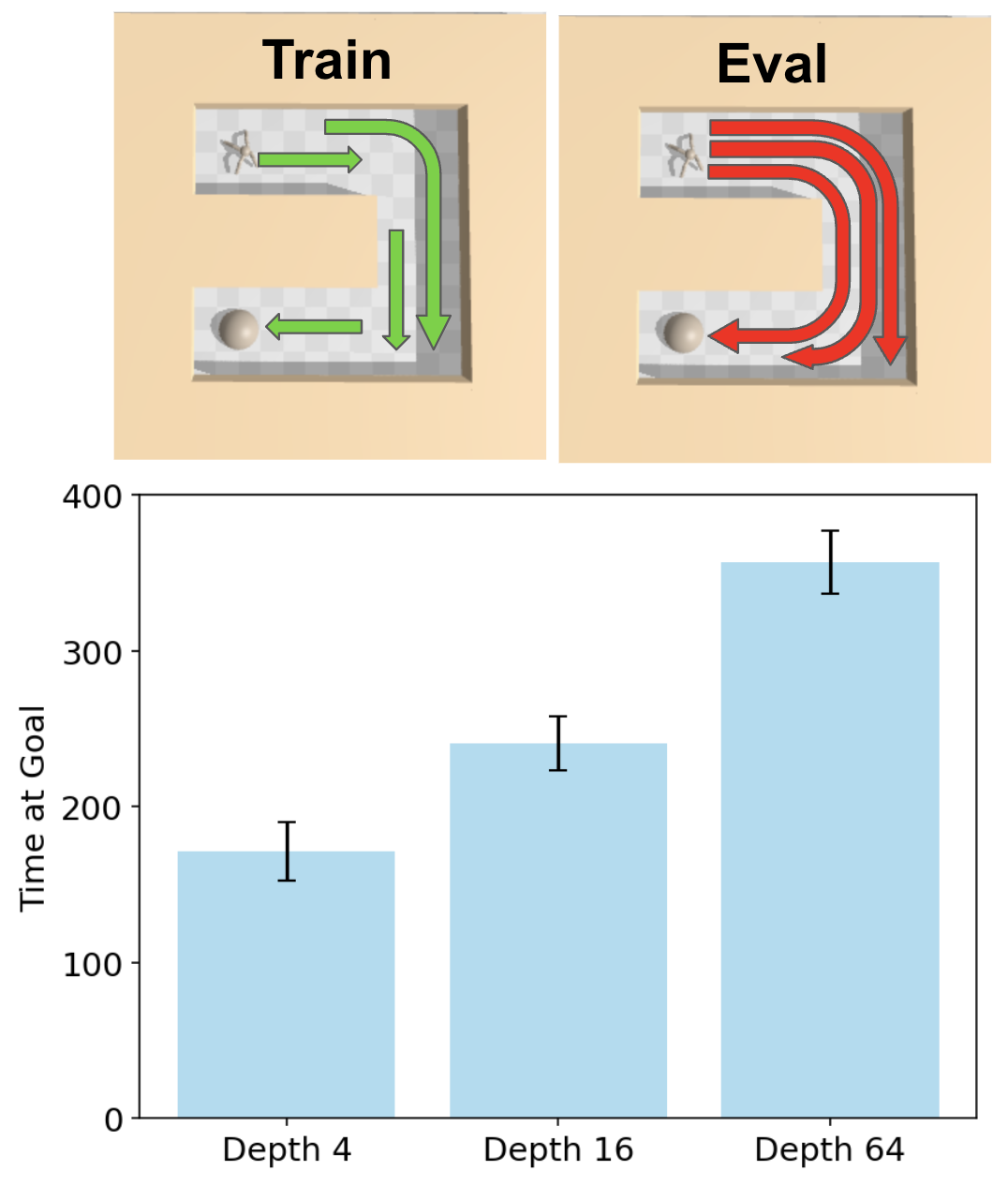
그림 11: 깊은 네트워크는 더 우수한 일반화 성능을 보인다.
(좌측 상단) Ant U-Maze 환경의 학습 설정을 수정하여, 시작–목표 쌍(start–goal pair)의 거리가 ≤ 3 유닛이 되도록 제한한다. 이 설계는 (우측 상단) 평가에 사용되는 어떤 시작–목표 쌍도 학습 중에 등장하지 않도록 보장하며, 경험 결합(stitching)을 통한 조합적 일반화 능력을 평가하기 위함이다.
(하단) 네트워크 깊이가 4에서 16, 64로 증가함에 따라 일반화 성능이 향상된다.
강화학습에서 또 하나의 핵심 과제는 학습 중에 경험하지 못한 태스크에 대해서도 일반화할 수 있는 정책을 학습하는 것이다. 이를 평가하기 위해 우리는 Ant U-Maze 환경을 수정한 버전을 설계했다. 그림 11(우측 상단)에 나타난 것처럼, 기존 JaxGCRL 벤치마크는 벽 반대편에 위치한 가장 먼 세 개의 목표 지점에 대해 에이전트의 성능을 평가한다. 그러나 본 연구에서는 모든 가능한 하위 목표(subgoal)에 대해 학습하는 대신(이는 평가용 상태–목표 쌍을 포함하는 상위 집합이 됨), 시작–목표 간 거리가 최대 3 유닛인 쌍만을 사용해 학습하도록 설정을 변경했다. 이를 통해 평가에 사용되는 시작–목표 쌍이 학습 데이터에 전혀 포함되지 않도록 했다.
그림 11의 결과에 따르면, 깊이 4의 네트워크는 일반화 능력이 제한적이며, 시작 지점에서 4 유닛 떨어진 가장 쉬운 목표만 해결할 수 있었다. 깊이 16 네트워크는 중간 수준의 성공을 보였고, 깊이 64 네트워크는 가장 어려운 목표 지점까지 해결하는 등 뛰어난 성능을 보였다. 이러한 결과는 네트워크 깊이가 증가함에 따라, 거리 ≤ 3 유닛의 부분적인 경험들을 결합(stitching)하여 U-Maze의 6 유닛 구간을 탐색할 수 있는 능력이 점진적으로 형성됨을 시사한다.
(CRL) 알고리즘의 핵심적 역할
부록 A에서는 확장된 CRL이 다른 목표 조건 강화학습 기준선 알고리즘들을 능가하며, 목표 조건 강화학습 분야의 최신 성능(SOTA)을 달성함을 보인다. 시간차 학습(temporal difference) 기반 방법들(SAC, SAC+HER, TD3+HER)의 경우, 네트워크 깊이가 4일 때 이미 성능이 포화되며, 그 이후 깊이를 더 늘려도 성능 향상이 거의 없거나 오히려 성능이 저하되는 현상이 관찰된다. 이는 이러한 방법들이 주로 네트워크 폭(width) 확장에서 이득을 얻는다는 기존 연구 결과와도 일치한다(Lee et al., 2024; Nauman et al., 2024b). 이러한 결과는 자기지도 CRL 알고리즘 자체가 확장 성능의 핵심 요소임을 시사한다.
또한 우리는 다른 자기지도 학습 알고리즘들, 즉 목표 조건 행동 복제(Goal-Conditioned Behavioral Cloning, GCBC)와 목표 조건 지도 학습(Goal-Conditioned Supervised Learning, GCSL)에 대해서도 확장 실험을 수행했다. 이들 방법은 일부 환경에서는 성공률이 0에 머물렀지만, 팔 조작(arm manipulation) 태스크에서는 일정 수준의 효용을 보였다. 흥미롭게도 GCBC와 같이 매우 단순한 자기지도 알고리즘조차도 네트워크 깊이를 증가시켰을 때 성능 향상의 이점을 얻는다. 이는 향후 연구에서 다른 자기지도 학습 방법들을 추가로 탐구함으로써, 자기지도 강화학습 확장을 위한 서로 다른 혹은 보완적인 스케일링 전략을 발견할 수 있음을 시사한다.
마지막으로, 최근 연구에서는 시간적 거리(temporal distance)가 삼각 부등식에 기반한 불변성(triangle inequality–based invariance)을 만족한다는 점을 활용하여, 준거리(quasimetric) 아키텍처를 목표 조건 강화학습에 결합하는 시도가 이루어지고 있다. 부록 A에서는 이러한 준거리 네트워크에 깊이 확장을 적용했을 때도 동일한 스케일링 효과가 유지되는지 여부를 함께 분석한다.
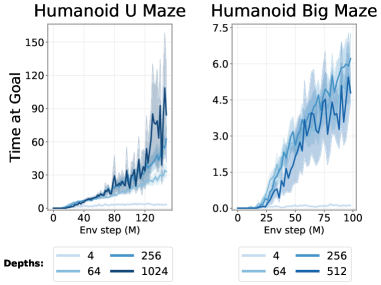
그림 12: 스케일링의 한계 테스트. 그림 1의 결과를 확장하여, 난이도가 높은 Humanoid 미로 환경에서 네트워크 규모를 더욱 키운 실험 결과를 제시한다. Humanoid U-Maze 환경에서 네트워크 깊이가 256층과 1024층에 이르러도 성능 향상이 지속됨을 확인했다. 단, 1024층 네트워크의 경우 학습 초기에 액터 손실(actor loss)이 발산하는 현상이 관찰되었기 때문에, 액터 네트워크의 깊이는 512로 유지하고 두 개의 크리틱 인코더에만 1024층 네트워크를 적용했다.
4.6 오프라인 Contrastive RL에서도 깊이 확장이 성능을 향상시키는가?
예비 실험으로, 우리는 OGBench(Park et al., 2024)를 사용하여 오프라인 목표 조건 강화학습 설정에서 CRL의 깊이 확장 효과를 평가했다. 그 결과, 오프라인 환경에서는 CRL 네트워크의 깊이를 증가시켜도 성능이 향상된다는 뚜렷한 증거를 찾지 못했다.
이를 보다 면밀히 분석하기 위해 다음과 같은 소거 실험(ablation)을 수행했다.
(1) 액터 네트워크의 깊이를 4 또는 8로 고정한 상태에서 크리틱 네트워크의 깊이만 확장하는 경우,
(2) 크리틱 인코더의 마지막 레이어들에 대해 콜드 초기화(cold initialization)를 적용하는 경우(Zheng et al., 2024).
모든 설정에서, 깊이 4의 기본 모델이 가장 높은 성공률을 보이는 경우가 많았다. 향후 연구의 중요한 방향은 본 연구의 방법을 오프라인 설정에서도 확장이 가능하도록 어떻게 적응시킬 수 있을지를 탐구하는 것이다.
5 결론
오늘날 비전 및 언어 모델의 많은 성공은 규모 확장(scale)으로부터 나타나는 발현적 능력(emergent capabilities)에 기인한다고 볼 수 있으며(Srivastava et al., 2023), 이로 인해 많은 시스템들이 강화학습 문제를 비전이나 언어 문제로 환원하는 방향을 택해왔다. 대규모 AI 모델에서 제기되는 핵심 질문 중 하나는 데이터는 어디에서 오는가이다. 지도 학습 패러다임과 달리, 강화학습은 탐색(exploration)을 통해 모델 학습과 데이터 수집 과정을 동시에 최적화함으로써 이 문제를 본질적으로 해결한다.
궁극적으로, 발현적 능력을 보여주는 강화학습 시스템을 효과적으로 구축하는 방법을 규명하는 것은, 강화학습 분야가 스스로 대규모 모델을 학습하는 분야로 도약하는 데 중요한 역할을 할 것이다. 우리는 본 연구가 그러한 시스템을 향한 하나의 발걸음이라고 믿는다. 강화학습 확장을 위한 핵심 구성 요소들을 하나의 접근법으로 통합함으로써, 복잡한 태스크에서도 모델 규모가 커질수록 성능이 일관되게 향상됨을 보여주었다. 더 나아가, 깊은 모델들은 목표에 도달하는 데 필요한 기술을 암묵적으로 학습한 것으로 해석할 수 있는, 질적으로 우수한 행동을 보인다.
한계점(Limitations)
본 연구의 주요 한계는 네트워크 깊이를 확장할수록 계산 비용(compute)이 크게 증가한다는 점이다. 향후 연구의 중요한 방향으로는, 분산 학습(distributed training)을 활용해 더 많은 계산 자원을 효율적으로 사용하는 방법과, 프루닝(pruning)이나 지식 증류(distillation)와 같은 기법을 통해 계산 비용을 줄이는 방안을 탐구하는 것이 있다.
영향 성명(Impact Statement)
본 논문은 머신러닝 분야의 발전을 목표로 한 연구를 제시한다. 본 연구가 가져올 수 있는 사회적 영향은 다양할 수 있으나, 본 논문에서는 특별히 강조해야 할 사항은 없다고 판단한다.
감사의 글(Acknowledgments)
본 연구는 NSF 지원을 통해 연구자 참여를 지원해준 Researcher Engagement 디렉터 Galen Collier와, 귀중한 도움을 제공해준 Princeton Research Computing의 스태프들에게 깊은 감사를 표한다. 또한 본 연구에 대한 논의와 기여를 해준 Colin Lu에게도 감사의 뜻을 전한다. 본 연구는 폴란드 국립과학센터(National Science Centre, Poland, grant no. 2023/51/D/ST6/01609)의 지원과, 바르샤바 공과대학교(Warsaw University of Technology)의 Excellence Initiative: Research University(IDUB) 프로그램의 부분적 지원을 받아 수행되었다. 마지막으로, 원고에 대해 유익한 의견과 피드백을 제공해준 Jens Tuyls와 Harshit Sikchi에게도 감사를 전한다.
부록 A 추가 실험(Appendix A: Additional Experiments)
A.1 확장된 CRL은 10개 환경 중 8개에서 모든 기준선 모델을 능가한다
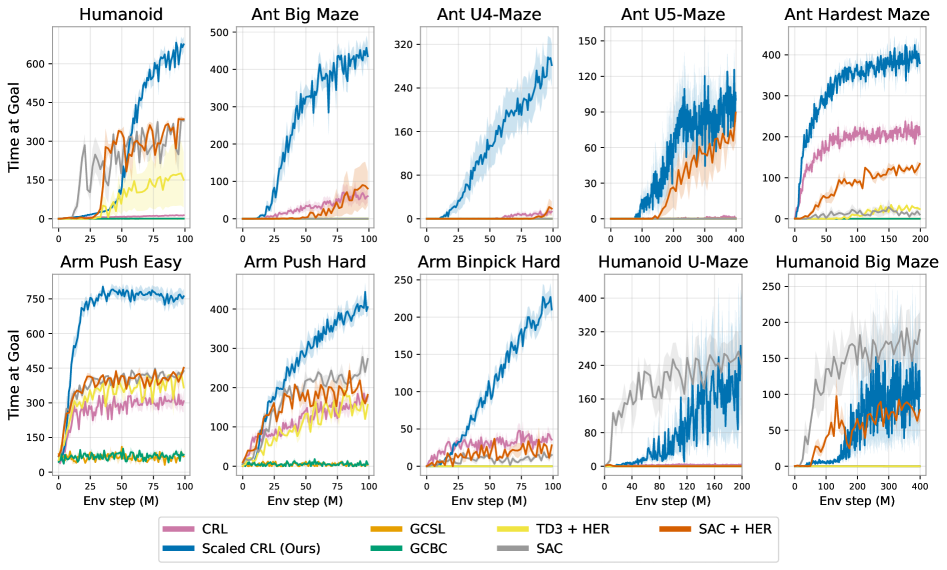
그림 12: 확장된 CRL(본 연구)은 기존 CRL(원본), SAC, SAC+HER, TD3+HER, GCSL, GCBC 기준선들을 10개 환경 중 8개에서 능가한다.
그림 1에서는 CRL 알고리즘의 네트워크 깊이를 증가시킬 경우 기존 CRL 대비 성능이 크게 향상됨을 보였다(표 1 참조). 여기서는 이러한 성능 향상이 온라인 목표 조건 강화학습 환경에서 최신 수준(state-of-the-art) 의 결과로 이어짐을 보여준다. 구체적으로, 확장된 CRL은 SAC, SAC+HER, TD3+HER와 같은 표준 TD 기반 방법들뿐만 아니라, GCBC와 GCSL과 같은 자기지도 모방 기반 접근법들보다도 우수한 성능을 달성한다.
A.2 CRL 알고리즘의 핵심성: 다른 기준선에서는 깊이 확장이 효과적이지 않다

그림 13: SAC, SAC+HER, TD3+HER, GCSL, GCBC에서는 깊이 확장이 제한적인 성능 향상만을 보인다.
다음으로, 기준선 알고리즘들에서 네트워크 깊이를 증가시켰을 때 CRL에서 관찰된 것과 유사한 성능 향상이 나타나는지 분석한다. 그 결과, SAC, SAC+HER, TD3+HER는 깊이를 4층을 초과해 늘려도 성능 향상을 거의 얻지 못했으며, 이는 기존 연구 결과와도 일치한다(Lee et al., 2024; Nauman et al., 2024b). 또한 GCSL과 GCBC는 Humanoid 및 Ant Big Maze 태스크에서 유의미한 성능을 전혀 달성하지 못했다. 흥미롭게도 한 가지 예외가 관찰되었는데, Arm Push Easy 환경에서는 GCBC가 네트워크 깊이를 늘렸을 때 성능 향상을 보였다.
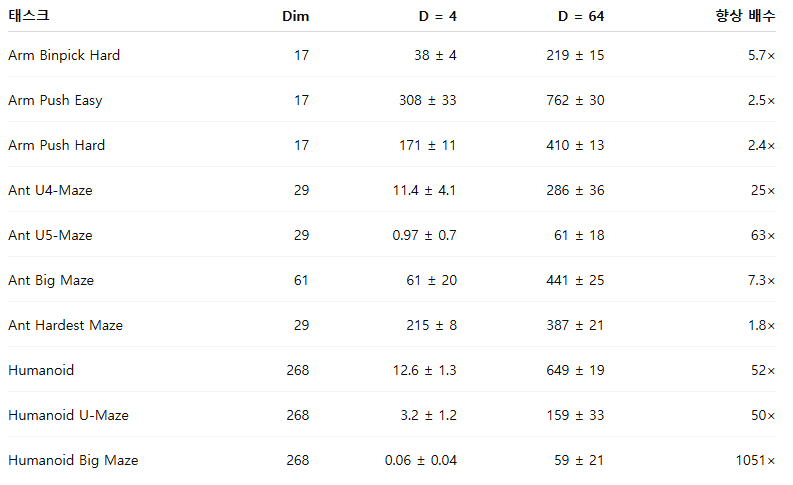
표 1: 네트워크 깊이를 증가시키면(깊이 D = 4 → 64) CRL의 성능이 향상된다(그림 1 참조). 깊이 확장의 효과는 관측 차원(Dim)이 클수록 더욱 크게 나타난다.
A.3 추가 스케일링 실험: 오프라인 GCBC, BC, QRL
우리는 여러 추가적인 스케일링 실험을 더 수행하였다. 그림 14에 나타난 바와 같이, 본 연구의 접근법은 OGBench의 antmaze-medium-stitch 태스크에서 오프라인 GCBC 설정에 대해 네트워크 깊이 확장을 성공적으로 달성한다. 이 과정에서 레이어 정규화(layer normalization), 잔차 연결(residual connections), Swish 활성화 함수의 조합이 핵심적임을 확인했으며, 이는 본 연구의 아키텍처 설계가 다른 알고리즘이나 설정에서도 깊이 확장을 가능하게 하는 데 적용될 수 있음을 시사한다.
반면, 행동 복제(Behavioral Cloning, BC)와 QRL(Wang et al., 2023a) 알고리즘에 대해서도 깊이 확장을 시도했으나, 두 경우 모두 성능이 오히려 저하되는 부정적인 결과가 관찰되었다.

그림 14: 본 연구의 방법은 OGBench의 antmaze-medium-stitch 환경에서 오프라인 GCBC에 대해 깊이 확장을 성공적으로 달성한다. 반면, BC(antmaze-giant-navigate, expert SAC 데이터)와 QRL의 경우에는 온라인(FetchPush) 및 오프라인(pointmaze-giant-stitch, OGBench) 설정 모두에서 깊이 확장이 부정적인 결과를 보였다.
A.4 준거리(quasimetric) 아키텍처에서도 깊이 확장이 효과적인가?
선행 연구(Wang et al., 2023b; Liu et al., 2023)에서는 시간적 거리(temporal distance)가 중요한 불변성(invariance) 특성을 만족함을 보였으며, 이를 바탕으로 시간적 거리를 학습할 때 준거리(quasimetric) 아키텍처를 사용하는 접근이 제안되었다. 본 절의 다음 실험에서는 아키텍처를 변경했을 때 자기지도 강화학습의 스케일링 특성이 유지되는지를 검증한다.
구체적으로 우리는 MRN 표현(MRN representations)을 사용하고, backward NCE 손실을 적용하는 CMD-1 알고리즘(Myers et al., 2024)을 활용한다. 실험 결과, 스케일링에 따른 이점이 단일한 신경망 파라미터화에만 국한되지 않음을 확인했다. 즉, 준거리 아키텍처를 결합한 경우에도 깊이 확장의 효과가 나타난다.
다만 MRN은 Ant U5-Maze 태스크에서 성능이 낮게 나타났으며, 이는 준거리 모델에서 일관된 스케일링 성능을 달성하기 위해서는 추가적인 아키텍처적 혁신이 필요함을 시사한다.
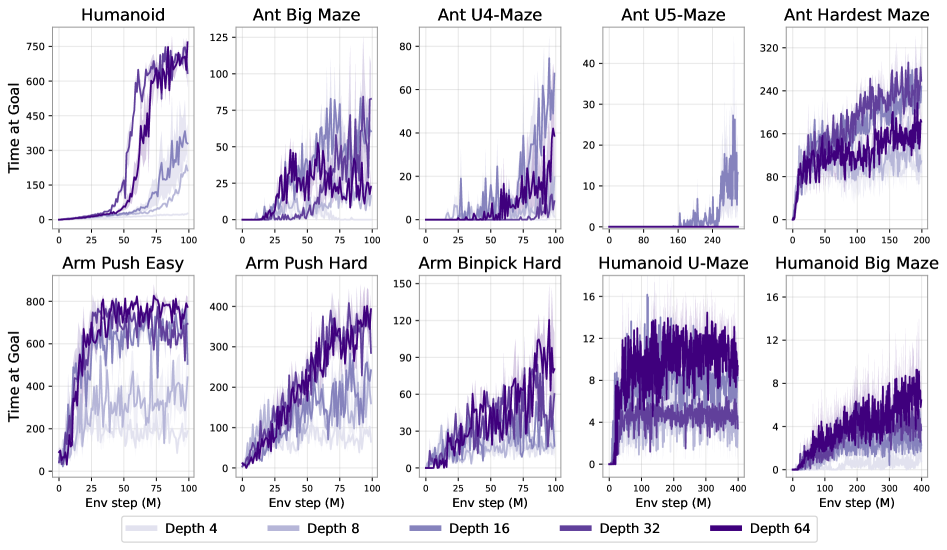
그림 15: 준거리 아키텍처(CMD-1)를 결합한 CRL에서 깊이 확장이 성능에 미치는 영향.
A.5 추가 아키텍처 소거 실험: 레이어 정규화와 Swish 활성화
본 절에서는 레이어 정규화(layer normalization)와 Swish 활성화 함수 선택의 타당성을 검증하기 위한 소거 실험(ablation)을 수행한다. 그림 16에서 확인할 수 있듯이, 레이어 정규화를 제거할 경우 성능이 현저히 저하된다. 또한 ReLU 활성화 함수를 사용해 깊이 확장을 시도하면, Swish 활성화를 사용할 때에 비해 확장성이 크게 저해된다.
이러한 결과는 그림 6의 분석과 함께, 잔차 연결(residual connections), 레이어 정규화, Swish 활성화 함수라는 세 가지 아키텍처 구성 요소가 서로 결합되어야만 깊이 확장의 잠재력을 온전히 발휘할 수 있음을 보여준다.
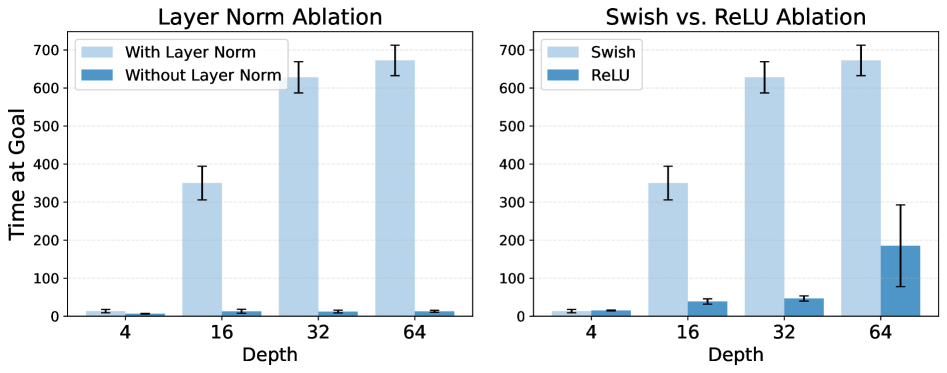
그림 16:
(좌) 깊이 확장을 위해서는 레이어 정규화가 필수적이다.
(우) ReLU 활성화를 사용한 깊이 확장은 Swish 활성화를 사용할 때보다 성능이 저하된다.
A.6 최근 등장한 RL 스케일링 문헌의 새로운 아키텍처 혁신을 통합할 수 있는가?
최근 Simba-v2는 확장 가능한 강화학습을 위한 새로운 아키텍처를 제안했다. 이 방법의 핵심 혁신은 레이어 정규화(layer normalization)를 초구면 정규화(hyperspherical normalization) 로 대체한 것이다. 초구면 정규화는 각 경사 하강 업데이트 이후 네트워크 가중치를 단위 노름(unit-norm)을 갖는 초구면(hypersphere) 위로 사영(project)한다.
실험 결과, 본 연구의 아키텍처에 초구면 정규화를 추가하더라도 깊이 확장에 따른 동일한 스케일링 경향이 유지되며, 나아가 깊이 확장의 샘플 효율성(sample efficiency) 이 더욱 향상됨을 확인했다. 이는 본 연구의 방법이 강화학습 스케일링 문헌에서 새롭게 등장하는 아키텍처 혁신들을 자연스럽게 통합할 수 있음을 보여준다.
표 2: 아키텍처에 초구면 정규화를 통합하면 깊이 확장의 샘플 효율성이 향상된다.

A.7 깊은 네트워크에서의 잔차 활성화 노름(Residual Norms)
선행 연구에서는 네트워크가 깊어질수록 잔차 활성화(residual activation)의 노름(norm)이 감소하는 경향이 관찰된 바 있다(Chang et al., 2018). 본 연구에서는 이러한 패턴이 우리의 설정에서도 유지되는지를 분석한다. 크리틱 네트워크의 경우, 특히 매우 깊은 아키텍처(예: 깊이 256)에서 이러한 감소 추세가 전반적으로 뚜렷하게 나타난다. 반면, 액터 네트워크에서는 이러한 효과가 상대적으로 덜 두드러진다.

그림 17: 깊이 32, 64, 128, 256인 네트워크에서 잔차 활성화의 L2 노름.
A.8 오프라인 목표 조건 강화학습에서의 깊이 확장
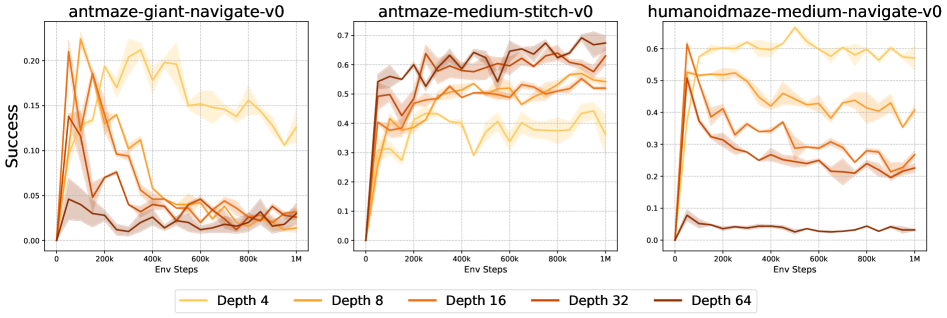
그림 18: 오프라인 설정에서 본 연구 방법의 확장성을 평가하기 위해, OGBench(Park et al., 2024)에서 모델 깊이를 확장하는 실험을 수행했다. 세 가지 환경 중 두 곳에서는 깊이를 4에서 64로 늘릴수록 성능이 급격히 저하되었으며, antmaze-medium-stitch-v0 환경에서만 소폭의 성능 향상이 관찰되었다. 오프라인 목표 조건 강화학습(GCRL)에서도 본 연구의 방법을 성공적으로 확장할 수 있도록 적응시키는 것은 향후 연구의 중요한 과제이다.
부록 B 실험 세부 사항(Appendix B: Experimental Details)
B.1 환경 설정 및 하이퍼파라미터

그림 19: 본 논문의 스케일링 결과는 JaxGCRL 벤치마크에서 검증되었으며, 보행(locomotion), 내비게이션(navigation), 조작(manipulation) 등 다양한 태스크 전반에 걸쳐 일관되게 재현됨을 보여준다. 이 태스크들은 보조 보상(auxiliary reward)이나 시연(demonstrations)이 전혀 제공되지 않는 온라인 목표 조건 강화학습 설정으로 구성되어 있다. 그림은 (Bortkiewicz et al., 2024)에서 인용하였다.
본 연구의 실험은 그림 19에 시각화된 JaxGCRL의 GPU 가속 환경 세트를 사용하며, 대비학습 기반 강화학습(contrastive RL) 알고리즘과 그에 대응하는 하이퍼파라미터는 표 7에 제시되어 있다. 구체적으로, 다음의 10개 환경을 사용하였다.
- ant_big_maze
- ant_hardest_maze
- arm_binpick_hard
- arm_push_easy
- arm_push_hard
- humanoid
- humanoid_big_maze
- humanoid_u_maze
- ant_u4_maze
- ant_u5_maze
B.2 파이썬 환경 차이(Python Environment Differences)
본 논문에 제시된 모든 그래프에서는 공정하고 일관된 비교를 위해 MJX 3.2.6과 Brax 0.10.1을 사용하였다. 개발 과정에서 우리는 사용 중이던 환경 버전(CleanRL 기반의 JaxGCRL)과, 보다 최근 커밋에서 권장된 JaxGCRL 버전(Bortkiewicz et al., 2024) 사이에 물리 시뮬레이션 동작의 차이가 존재함을 발견했다. 분석 결과, 그림 20에 나타난 성능 차이는 MJX 및 Brax 패키지 버전의 차이에서 기인한 것으로 확인되었다.

그럼에도 불구하고, 두 가지 MJX 및 Brax 버전 설정 모두에서 네트워크 깊이가 증가함에 따라 성능이 단조롭게(monotonically) 향상되는 동일한 스케일링 경향이 관찰된다.
그림 20: 두 가지 서로 다른 파이썬 환경에서의 Humanoid 태스크 스케일링 동작 비교.
(MJX=3.2.3, Brax=0.10.5)와 (MJX=3.2.6, Brax=0.10.1, 본 연구에서 사용한 JaxGCRL 버전).
두 환경 모두에서 깊이 확장은 성능을 크게 향상시킨다. 본 연구에서 사용한 환경에서는, 다른 파이썬 환경에 비해 더 적은 환경 스텝으로도 약간 더 높은 성능에 도달함을 확인할 수 있다.
B.3 본 접근법의 실제 경과 시간(Wall-clock Time)
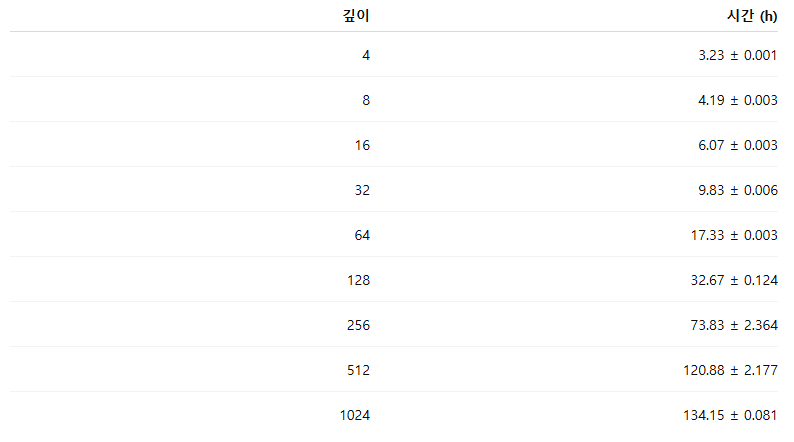
표 3에는 본 연구에서 사용한 접근법의 실제 경과 시간(wall-clock time)을 보고한다. 해당 표는 10개 모든 환경에 대해 깊이 4, 8, 16, 32, 64 설정의 결과를 제시하며, Humanoid U-Maze 환경의 경우 최대 1024층까지 확장한 결과도 포함한다. 전반적으로, 일정 깊이 이후부터는 네트워크 깊이에 따라 실제 학습 시간이 거의 선형적으로 증가하는 경향을 보인다.
표 3: 10개 모든 환경에서 깊이 4, 8, 16, 32, 64에 대한 실제 경과 시간(단위: 시간)
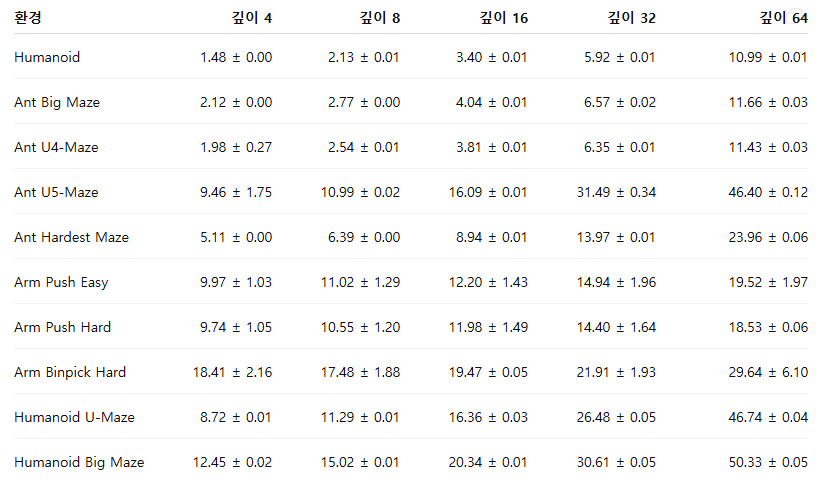
표 4: Humanoid U-Maze 환경에서 깊이 4부터 1024까지 학습했을 때의 총 실제 경과 시간(단위: 시간)
B.4 실제 경과 시간(Wall-clock Time): 기준선과의 비교
기준선 알고리즘들은 표준 크기의 네트워크를 사용하므로, 확장된 본 접근법은 환경 스텝당 실제 경과 시간이 더 많이 소요되는 것이 자연스럽다(표 5 참조). 그러나 보다 실용적인 지표는 특정 성능 수준에 도달하는 데 필요한 시간이다. 표 6에서 보이듯이, 본 연구의 방법은 10개 환경 중 7개에서 가장 강력한 기준선인 SAC를 더 적은 실제 경과 시간으로 능가한다.
표 5: 10개 모든 환경에서 본 방법과 기준선들의 실제 학습 시간 비교(단위: 시간)
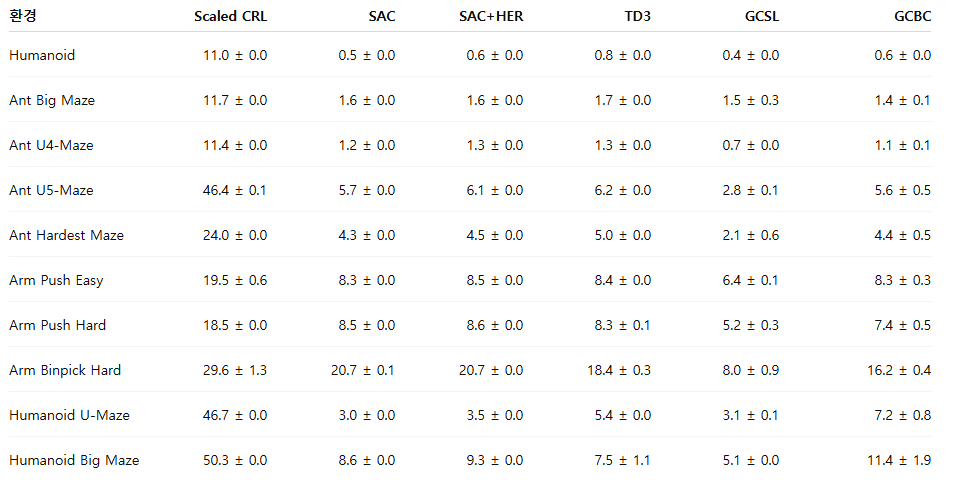
표 6: SAC의 최종 성능을 초과하는 데 필요한 실제 경과 시간(단위: 시간).
10개 환경 중 7개에서 본 방법이 SAC보다 더 짧은 시간 내에 이를 달성한다.
N/A는 해당 환경에서 확장된 CRL이 SAC를 능가하지 못했음을 의미한다.

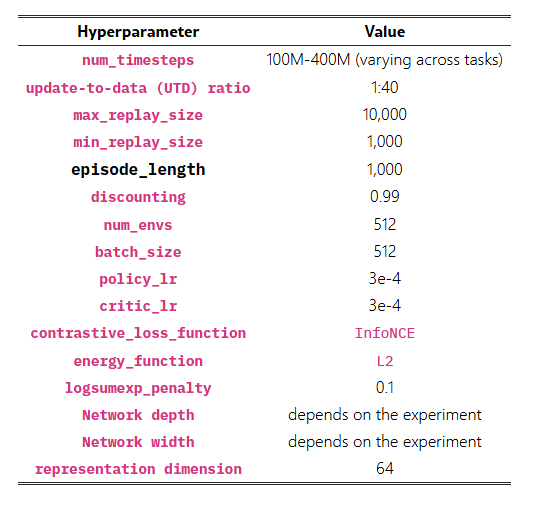
표 7: 하이퍼파라미터